双向振动下含黏粒砂土液化特性试验研究

黄志全， 王伟， 张瑞琪， 张晓丽

(华北水利水电大学,河南 郑州 450045)

wi= σzddεzd+σθddεθd+σrddεrd+τddεzθd 。

W=∑wi。



双向振动下含黏粒砂土液化特性试验研究

黄志全， 王伟， 张瑞琪， 张晓丽

(华北水利水电大学,河南 郑州 450045)

采用GCTS双向动三轴测试系统，把膨润土作为试验的黏粒材料，通过饱和砂土的双向动三轴试验，以试样液化的耗损能量为指标，探究不同黏粒含量、干密度、围压及相位差对饱和砂土液化特性的影响。结果表明：随着黏粒含量的增加，砂土液化所需的耗损能量先减少后增加，呈抛物线型，这是因为黏粒含量较低时，黏粒在砂颗粒间起到润滑的作用，随着黏粒含量的增多，黏粒反而起到固定和镶嵌砂颗粒的作用；随着干密度和围压的增大，砂土液化所需的耗损能量不断增加；相位差为180°时更有利于饱和砂土的液化，而相位差的变化与砂土液化所需耗损能量之间的关系不明显。

双向动三轴；累计耗损能量；砂土液化；黏粒含量；相位差

我国是世界上地震灾害最为严重的国家之一，其中饱和土的液化是地震破坏的重要原因。纵观近几十年历史上的强震，饱和土的液化导致了地震发生时建筑物毁灭性的破坏，自1960年智利地震和1964年日本新泻地震出现了不同程度的喷水冒砂、地面下降等灾害现象，使得人们开始深入研究土的液化。

其中关于循环荷载下砂土孔压和损耗能量关系的研究最早开始于1970年，Youd首次提出了砂土能量栅的概念，当时所提出的能量栅只是一个定性的概念，但在一定程度上能够表明砂土结构的变化必然伴随着一定的能量耗损[1]。 Nemat和Shokooh提出了基于能量法的土壤液化特性分析方法，从能量角度研究了振动荷载下砂土孔压增长机理，并建立了数学模型[2]。Davis与Berrill在前人研究的基础上，从热力学的角度建立了砂土孔压的增长与耗损能量之间的关系；1982年，他们进行了更深入的研究，推导出了地震场地砂土液化的统计判别式[3]。Cao和加拿大的Law通过实验室振动三轴和振动扭剪试验获得了砂土的孔压比与土体振动耗损能量之间的指数表达式，并由试验获得的土体液化的孔压与耗损能量表达式，结合国内外砂土及粉砂场地地震液化的统计分析成果，获得了适用于粉砂和砂土的场地液化势的统计判别式[4]。随后，他们通过室内振动三轴试验研究了砂粒含量和黏粒含量对土体液化强度以及对孔压与能量关系模式的影响[4]。Baziar等通过动扭剪试验，利用能量法研究了砂土的液化特性，发现细粒含量和有效围压对砂土的液化特性有很大影响[5]。Polito等开展了不同波形的循环三轴试验，发现饱和松砂的液化耗损能量与加载波形没有关系[6]。Lade等的研究结果表明，细粒含量的增加降低了饱和砂土的抗液化能力[7-8]。Amini等研究则发现细粒含量的增加提高了饱和砂土的抗液化能力[9]。

以上对砂土液化特性的研究多是在没有考虑径向荷载作用下进行的，大多利用单向振动时试样 45°面上的应力来模拟地震剪切波的作用，并且认为地震荷载的破坏作用主要是由剪切荷载引起的。谢定义认为，地震剪切波的试验应该用双向振动三轴仪在轴向和径向施加同频率、等幅值、相位差为 180°的循环荷载来模拟[10]。另外，大多数情况下，土体所受到的动荷载作用十分复杂，尤其是砂土地基在强震作用下同时受 P 波和 S 波作用，此时土体不仅承受剪切动荷载作用，还同时受到压缩动荷载作用[11]。因此，在抗震设计中径向压缩动荷载的作用显然不能忽略。

综上所述，在双向循环动荷载下并结合能量损耗来研究砂土液化的特性至今较少。笔者以双向循环加载的累积耗损能量为指标，通过饱和砂土的循环三轴试验，探讨黏粒含量、干密度、围压以及相位差等因素对砂土液化特性的影响。

1 理论基础

土体在循环动荷载作用下，其振动能量一部分被释放，另一部分被土体所吸收，其中被土体吸收的那部分能量称之为耗损能量。而在循环动荷载作用下，饱和砂土在不排水条件下振动孔隙水压力的增大，主要是由于砂土在一定的强度振动下，土颗粒之间会发生相互运动，颗粒重新排列，特别是饱和砂土，在振动过程中土骨架趋于松弛，粒间作用的应力相应转换为孔隙水压力，因此，振动孔隙水压力的增大与在振动过程中消耗的能量有关。那么，假定砂土试样单位体积内第i循环的耗损能量表示为wi,在动三轴试验中，每次循环荷载作用下试样的耗损能量W等于每次循环形成的应力-应变关系滞回圈的面积，可通过数学积分计算获得，即：

wi=σzddεzd+σθddεθd+σrddεrd+τddεzθd。

单位体积土体累积的耗损能量为各次循环损失能量之和，即：

W=∑wi。

式中：σzd、σθd、σrd分别为竖向、环向和径向的循环应力；εzd、εθd、εrd分别为竖向、环向和径向的循环应变；τd、εzθd分别为循环剪应力和循环剪应变。

2 双向动三轴试验

2.1 试验材料及制备

试验所用土样全部是重塑土样，主要由细砂和黏粒配置而成，为了消除其他不确定因素的影响，对所用砂土进行预处理，即砂样经过烘干后，过0.25 mm和0.075 mm筛，选取粒径在0.075～0.25 mm范围内的砂粒备用，黏粒含量为0%。试验所用砂土样取自南水北调中线工程河北磁县漳河北岸段的一砂坡处，所取土样埋深约4 m，砂土基本物理情况见表1。试验所用黏粒出自白色膨润土，其主要成分为蒙脱石，含量95%，胀缩性很强。

表1 砂土的基本物理性质指标值

试样制样时按照干密度和黏粒含量的变化，根据试样的体积确定每个试样中砂土和黏粒的质量，将两者混在一起拌合均匀，加入一定的无气水，控制含水率为15%，将其储存在塑料袋内静置于保湿缸24 h后取出，试样采用直径50 mm，高100 mm的试样，分5层压实，根据试样总质量确定每层的质量，击实到相应高度，注意每层接触面的刮毛，保证试样完整性。

2.2 试验方案

本文采用GCTS双向动三轴测试系统，通过调整围压、轴向和径向振幅、振动频率、相位差等控制条件来研究不同情况下砂土液化的特性。试验中采用标准制样器制样，抽真空、饱和并冰冻后装样；再在小围压下解冻并通入无气水，然后测试孔压比，当孔压比达到一定值时表明试样已经饱和，方可进行下一步试验。试验破坏标准采用变形标准(εd=5%)，并根据经验设置振动循环次数，保证每次试样破坏时孔压比和变形都能达到破坏值。试验方案见表2。

表2 动三轴试验方案

3 结果分析

限于篇幅，本文以黏粒含量为5.0%的试样为例分析砂土液化的试验结果。选取其中干密度为1.50 g/cm3、围压100 kPa、相位差0°的试样，对该试样施加轴向140 kPa、径向30 kPa的双向循环荷载，随着循环振次的增加，孔压逐渐上升，由于径向循环荷载的施加，当孔压平均值接近于围压100 kPa时，认为砂土已经液化，试验结果如图1—3所示。图1给出了试样从加载到液化直至破坏的轴向应力-应变关系滞回圈，从图1中可以看出割线模量随着振次的增加逐渐降低。从图2中可以看出，在平均孔压达到80 kPa前，孔压随着耗损能量的增加呈线性增长的趋势，当平均孔压超过80 kPa时，孔压增加趋势逐渐变缓，且平均孔压最终接近于100 kPa，并且孔压随着振次的增加逐渐上升。图3是耗损能量与孔压的关系曲线，其中耗损能量是根据式(1)计算每次循环的应力-应变滞回圈面积得出来的，由于本次试验施加了轴向和径向循环荷载，故没有考虑环向应力、应变。

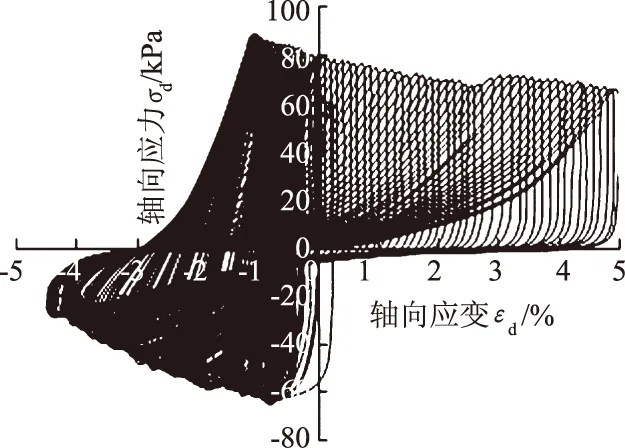
图1 轴向循环应力-应变滞回圈

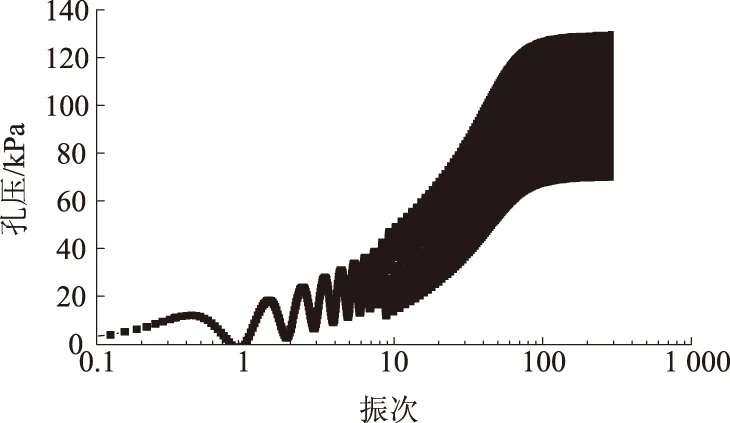
图2 孔压与循环振次的关系

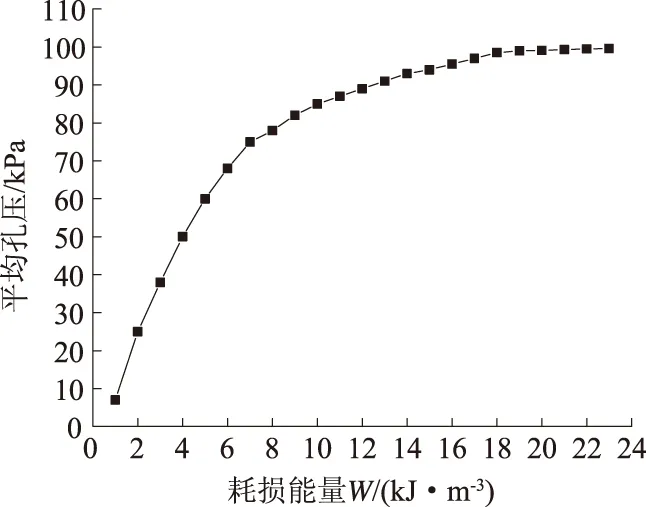
图3 累积耗损能量与孔压的关系

3.1 黏粒含量对砂土液化特性的影响

相关研究已表明，黏粒含量的不同对于饱和砂土的液化有很大的影响。

图4给出了围压为100 kPa、不同黏粒含量的砂土液化时的耗损能量。从图中可以看出，黏粒含量为10.0%的饱和砂土液化时的耗损能量明显低于其他含黏粒的砂土，而黏粒含量为12.5%的饱和砂土液化时的耗损能量高出黏粒含量为10.0%的很多，这说明砂土的抗液化能力并不是随着黏粒含量的增加而单调增加的。究其原因，从砂粒和黏粒的微观结构来看，无论是圆颗粒还是片状结构砂粒，黏粒分布在砂粒周围以点接触的形式和砂粒胶结在一起，当黏粒较少时，黏粒不能占满砂粒之间的空隙，黏粒的存在起到一定的润滑作用，使得在低黏粒含量下随着黏粒含量的增大，砂土的抗液化能力逐渐降低；当黏粒含量达到一定值时，黏粒能够占满砂颗粒之间的空隙，此时的黏粒不再起到润滑的作用，相反主要起稳定、镶嵌砂粒的作用，砂土开始表现出黏性土的特性，从而砂土抗液化的能力越来越强。因此，图4中曲线呈开口向上的近似抛物线，这与前人的研究成果基本一致[12]。但是，由于所加黏粒为蒙脱石含量较高的膨润土，鉴于膨润土特殊的膨胀性，使得在低黏粒含量情况下，试样中的黏粒能够更多地占据砂颗粒之间的空隙，因此抛物线的最低点要比衡朝阳等人研究得出的略低一些[13-14]。

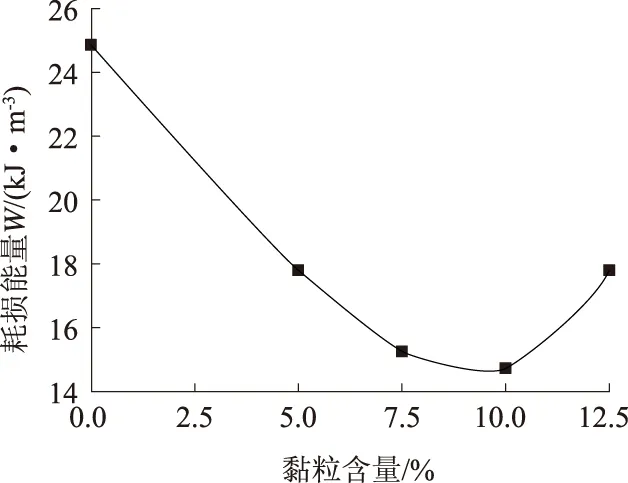
图4 黏粒含量与液化耗损能量的关系

3.2 干密度和围压对砂土液化特性的影响

关于干密度和围压对砂土液化特性的影响，前人的大多研究成果都是单向振动下并且很少以能量指标来分析干密度和围压对砂土液化特性的影响[15]。图5给出了围压为100 kPa、黏粒含量为5.0%、7.5%、10.0%时3种干密度下试样液化的耗损能量。由图可以看出，其他条件一样时，随着干密度的增大，累积耗损能量呈线性增加，砂土抗液化能力增强。

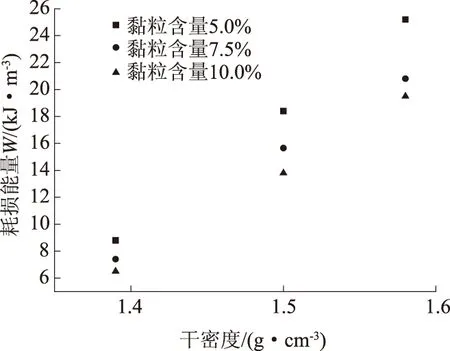
图5 干密度与砂土液化耗损能量的关系

图6给出了不同围压下试样累积耗损能量，由图可知，随着围压的增加，砂土液化损耗能量也相应增加，即砂土抗液化能力增强。

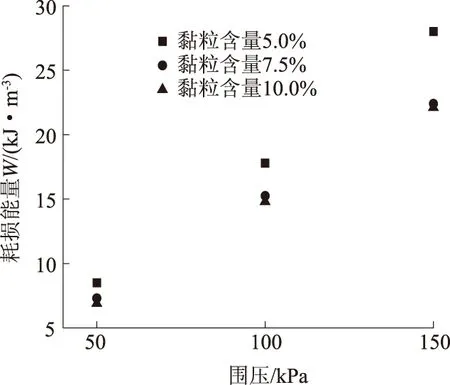
图6 围压与耗损能量的关系

3.3 相位差对饱和砂土液化特性的影响

以围压100 kPa为例，图7给出了相位差与砂土液化振次的关系曲线。由图7可以看出，在其他条件相同的情况下，随着相位差的变化，试样液化振次有着明显的变化规律，相位差由0°到180°对应的液化振次越来越少。出现这种现象的原因是施加双向循环荷载的相位差不同，将导致应力路径的不同，相位差为180°时，应力路径的倾斜斜率要比0°时斜率大，相应的应变增加速率较快，破坏时的振次较低。

图7 相位差与砂土液化振次的关系

对于相位差与砂土液化耗损能量的关系，以围压50、100、150 kPa为例，图8给出了相位差与耗损能量的关系曲线。

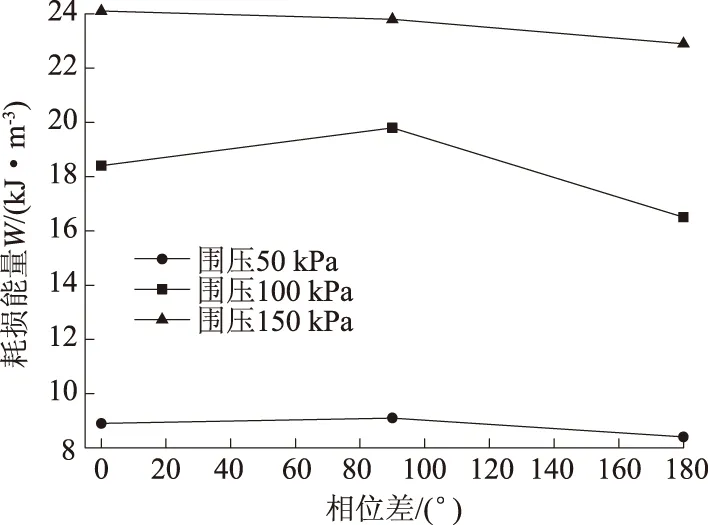
图8 相位差与砂土液化耗损能量的关系

由图8可知，相位差与耗损能量没有明显的关系，对于不同的相位差，试样液化耗损能量相差不大，究其原因，砂土液化耗损能量是由试样自身的物理性质决定的，与外部荷载施加的方式无关。

4 结 语

本文利用双向动三轴测试系统进行了饱和砂土在双向循环动荷载作用下的液化试验，以能量耗损为指标，主要分析了黏粒含量、干密度、围压及相位差对砂土液化特性的影响，得到以下结论：

1)黏粒含量对饱和砂土液化有着很大的影响，砂土的液化损耗能量不是随着黏粒含量的增加而单调增加，而是会出现一个低谷值，由于文中试验所加黏粒的膨胀性，使得抛物线的低谷值与其他人的研究结果有一定的差别。

2)双向循环动荷载下干密度和围压对砂土液化特性的影响与单向振动下基本一致，液化损耗能量随着干密度和围压的增大而增大，砂土的抗液化能力随之增强。

3)相位差对于砂土液化损耗能量影响不大，但是不同的相位差对应的液化振次有明显的区别，相位差为180°时更有利于砂土的液化。

4)本文研究的因素较少，特别是双向循环动荷载下振幅比对砂土液化特性的影响有待进一步研究。

[1]YOUD T L.Densification and shear of sand during vibration[J].Journal of the Soil Mechanics and Foundation Division,1970,96(3):863-880.

[2]NEMAT-NASSER S,SHOKOOH A.Unified approach to densification and liquefaction of coheionless sand in cyclic shearing[J].Canadian Geotechnical Journal,1979,16(4):659-678.

[3]DAVIS R O,BERRILL J B.Energy disslpation and seismic liquefaction in sands[J].Earthquake Engineering and Structural Dynamics,1982,10(1):59-68.[4]CAO Y L,LAW K J.Energy approach for liquefaction of sandy and clayey silts[C]∥Proceedings of Second International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics.St.Louis:Missouri Press,1991:491-497.

[5]BAZIAR M H,SHARAFI H.Assessment of silty sand liquefaction potential using hollow torsional tests：an energy approach[J].Soil Dynamics and Earthquake Engineering,2011,31(7):857-865.

[6]POLITO C P,GREEN R A,DILLON E,et al.Effect of load shape on relationship between dissipated energy and residual excess pore pressure generation in cyclic triaxial tests[J].Canadian Geotechnical Journal,2013,50(11):1118-1128.

[7]LADE P V,YAMAMURO J A.Effects of nonplastic fines on static liquefaction of sands[J].Canadian Geotechnical Journa1,1997,34(6):918-928.

[8]VAID Y P,FISHER J M,KUERBIS R H,et al.Particle gradation and liquefaction[J].Journal of Geotechnical Engineering,1990,116(4):698-703.

[9]AMINI F,QI G Z.Liquefaction testing of stratified silty sands[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(3):208-217.

[10]谢定义.土动力学[M].北京:高等教育出版社,2011：68-75.

[11]蔡袁强,王军,海钧.双向激振循环荷载作用下饱和软黏土强度和变形特性研究[J].岩石力学与工程学报, 2008,27(3):495-504.

[12]吴建平,吴世明.动荷载下含黏粒砂土的特性[C]∥中国水利学会岩土力学专业委员会.全国土工建筑物及地基抗震学术讨论会论文汇编.西安:陕西机械学院印刷厂,1986：265-268.

[13]衡朝阳,何满潮,裘以惠.含黏粒砂土抗液化性能的试验研究[J].工程地质学报,2001,9 (4): 339-344.

[14]XENAKI V C, ATHANASOPOULOS G A.Liquefaction resistance of sand-silt mixtures:an experimental investigation of the effect of fines[J].Soil Dynamics and Earthquake Engineering,2003,23:183-194.[15]王桂首,桑野二郎,竹村次郎.循环荷载下砂质混合土孔隙水压力特性研究[J].岩土工程学报,2004,26(4):541-545.

(责任编辑：乔翠平)

Experimental Study on Liquefaction Properties of Clayey Sand under Two-directional Cyclic Vibration

HUANG Zhiquan, WANG Wei， ZHANG Ruiqi， ZHANG Xiaoli

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

To study the liquefaction properties of clayey sand under two-directional cyclic vibration, we used the two-directional cyclic triaxial testing system and took bentonite as the experimental clay materials, the two-directional cyclic triaxial test on the saturated clayey sand was done.We took the liquefaction energy dissipation as the index and discussed the influence of the content of clay particles, the dry density, the confining pressure and the phase difference on the liquefaction properties of clayey sand. The results show: the dissipated energy needed by the sand liquefaction firstly decrease and then increase with the increase of the content of clay particles, and the curve is a parabola type, the reason is that the clay particles have a lubrication action among the particles of clayey sand when the content of clay particles is lower; the dissipated energy needed by the clayey sand liquefaction is increasing with the increase of the dry density and the confining pressure; the phase difference of 180° benefits the liquefaction of saturated sand, the relationships between the variation of the phase difference and the dissipated energy needed by the liquefaction of clayey sand is not obvious.

two-directional cyclic triaxial system; cumulative dissipated energy; sand liquefaction; the content of clay particles; phase difference

2016-01-20

河南省科技创新人才计划(154100510006)；河南省重点科技攻关项目(152102210111)；新疆维吾尔自治区科技援疆项目(201491105)；新疆自治区高层次人才引进工程资助。

黄志全(1970—)，男，河南潢川人，教授，博导，博士，主要从事岩土力学、边坡与滑坡工程等方面的研究。E-mail: huangzhiquan@ncwu.edu.cn。

王伟(1989—)，男，河南郑州人，硕士，主要从事岩土工程方面的研究。E-mail:961904565@qq.com。

10.3969/j.issn.1002-5634.2016.03.011

TV16；TU411

A

1002-5634(2016)03-0055-05