开放式电阻抗成像下的目标定位

林椹尠，程庆涛，惠小强

(1.西安邮电大学 理学院，陕西 西安 710121；2.西安邮电大学 通信与信息工程学院 陕西 西安 710121；3.西安邮电大学 物联网与两化融合研究院， 陕西 西安 710061)



开放式电阻抗成像下的目标定位

林椹尠1，程庆涛2，惠小强3

(1.西安邮电大学 理学院，陕西 西安 710121；2.西安邮电大学 通信与信息工程学院 陕西 西安 710121；3.西安邮电大学 物联网与两化融合研究院， 陕西 西安 710061)

给出一种开放式电阻抗成像中目标小圆圆心的近似位置和半径大小定位方法。利用Comsol multiphysics工具建立开放式电阻抗成像模型，测量并记录圆心在不同位置及半径大小不同时的各电极电势，计算相邻电极点之间的电势差。通过分析边界电势差与圆心的近似位置和半径大小的对应关系，利用电势差分析法和二分法进行目标定位。对比实验结果表明，相对电势差分析法可快速确定目标小圆的近似位置，具有普遍性；二分法可准确确定目标小圆的半径大小，具有较高精度。

开放式电阻抗成像；电势差分析法；二分法

电阻抗成像是一种两相流/多相流检测技术，主要应用在人体监护、临床成像等方面[1]。电阻抗成像分为封闭式电阻抗成像和开放式电阻抗成像。封闭式电阻抗成像电极围成的区域是封闭的，每次测量都要求电极均匀排放，存在着电极定位不准确，操作不便等问题[2-4]。开放式电阻抗成像可以较好地克服电极定位不准确、操作不便等问题，但其分辨率较低[5-7]。在现实的应用中，有时只需要定性判断目标的有无和大概位置，并不要求很高的成像分辨率，只要能找到边界电压和目标大小位置的对应规律即可，因此，开放式电阻成像应用较为广泛。

Comsol multiphysics是一款有限元仿真软件。通过求解偏微分方程(单场)或偏微分方程组(多场)来实现对真实物理现象的仿真。在Comsol multiphysics中可建立开放式电阻抗成像模型，通过模型内部移动成像目标，测量并记录边界电极电势[8-10]。本文以Comsol multiphysics为工具，构建开放式电阻抗成像模型，分析边界电势差与目标小圆大小及位置的对应规律，利用电势差分析法和二分法确定目标小圆圆心的近似位置和半径大小。

1　开放式电阻抗成像原理及模型

1.1开放式电阻抗成像原理

开放式电阻抗成像系统中，电极覆盖了整体边界上很小的一段，有效的成像区域只是电极覆盖下的浅表局部区域而不是对象整体，成像区域相对于对象整体是开放性的[11-12]。当成像区域被视为准静态场时，场内任意一点都满足麦克斯韦方程组[13]，可表示为

通过麦克斯韦方程组可得出该区域的电势分布函数φ和电导率分布函数σ满足拉普拉斯方程[14]的表达式为

(x,y)∈Ω,

其边界条件为[14]

(1)

1.2开放式电阻抗成像模型

利用Comsol multiphysics构建一个矩形平面，在其上挖一个半径为r的小圆并补上不同电导率的介质。在矩形的上边界均匀添加17个电极，左端是电流输入端，右端是接地端，输入电流为0.01 A，矩形的电导率是10-5s/m，目标小圆的电导率是0.01 s/m，半径为r，圆心坐标为(x,y)，y就是小圆圆心距表面的深度，也是小圆所能取到的最大半径。开放式电阻抗成像模型如图1所示。

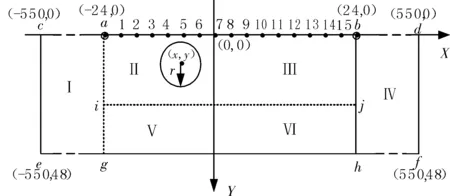
图1　开放式电阻抗成像模型

根据开放式电阻抗成像原理，电极只覆盖了整体边界上很小的一段。定义模型长度的边界尺寸为

C1=l1/l2。

式中l1为电极a和电极b之间的距离，l2为点C和点d之间的距离。

当电流从电极a输入，电极b输出时，目标小圆距离电极阵列越远所引起的电势差变化越小。定义模型深度的边界尺寸为

C2=l3/l4。

式中l3为电极a和点i之间的距离，l4为电极a和点g之间的距离。

为保证模型的开放性，设

l1=48 cm，l2=1 100 cm,

l3=8 cm，l4=48 cm，

那么

C1=1/23，C1=1/6。

2　目标小圆与边界电势差的关系

2.1圆心位置与边界电势差的关系

假定小圆半径已知。根据边界条件式(1)和式(2)，得出小圆圆心在模型成像区域(Ⅱ,Ⅲ)内每次移动的边界电势变化，计算相邻电极点电势差并拟合曲线，观察边界电势差波动和圆心近似位置之间的变化规律，利用电势差分析法确定圆心的近似位置。电势差分析法分为绝对电势差分析法和相对电势差分析法。二者主要区别在于前者电势差的值源于相邻点电势之差，后者电势差的值是在前者电势差的基础上减去没有成像目标时实验测得的边界电势。

2.2半径与边界电势差的关系

假定圆心位置已知，半径r未知。由图1可知，圆心坐标y就是成像目标所能取到的最大半径，所以小圆半径r的范围位于[0,y]之间，利用二分法，取r1=y/2。比较半径为r1和r时的绝对电势差变化，可以确定小圆半径是位于[0,y/2]还是[y/2,y]之间，如果位于[0,y/2]，取r2=y/4，比较半径为r1和r2时的绝对电势差变化，可以确定小圆半径是位于[0,y/4]还是[y/4,y/2]之间。依此类推，直至确定小圆的半径大小。

3　实验结果及分析

分别利用绝对电势差分析法、相对电势差分析法和二分法确定小圆近似位置和半径大小，拟合成曲线，通过对比选择更为合适的定位方法。对于圆心的近似位置，设置深度y=4 cm、小圆半径r=2 cm；对于小圆的半径大小，设置小圆圆心位于(9,4)。

3.1确定圆心近似位置方法对比

(1)绝对电势差分析法

分别设置小圆圆心位于(-9,4)、(9,4)、(-24,4)、(-22.5,4)和(-21,4)，对应位置上的绝对电势差变化分别如图2和图3所示。

图2　圆心位于(-9,4),(9,4) 的绝对电势差变化

图3　圆心位于(-24,4),(-22.5,4),(-21,4)的绝对电势差变化

由图2可知，图1中成像区域(Ⅱ,Ⅲ)内没有成像目标(相同介质)时，电势差曲线图是一条“U”型线。当Ⅱ(Ⅲ)区域内有成像目标时，“U”型线的左(右)出现了凹陷，凹陷处和圆心的近似位置存在一一对应关系。由图3可知，当成像区域(Ⅱ,Ⅲ)内有成像目标时，图中并没有明显的凹陷，无法确定小圆圆心的近似位置，所以绝对电势差分析法不够完善。

(2)相对电势差分析法

分别设置小圆圆心位于(-9,4)、(9,4)、(-24,4)、(-22.5,4)和(-21,4)，对应位置上的相对电势差变化如图4和图5所示。

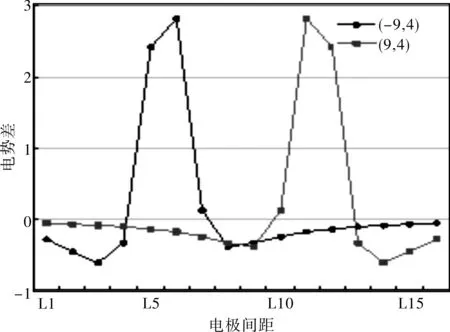
图4　圆心位于(-9,4)，(9,4) 的相对电势差变化

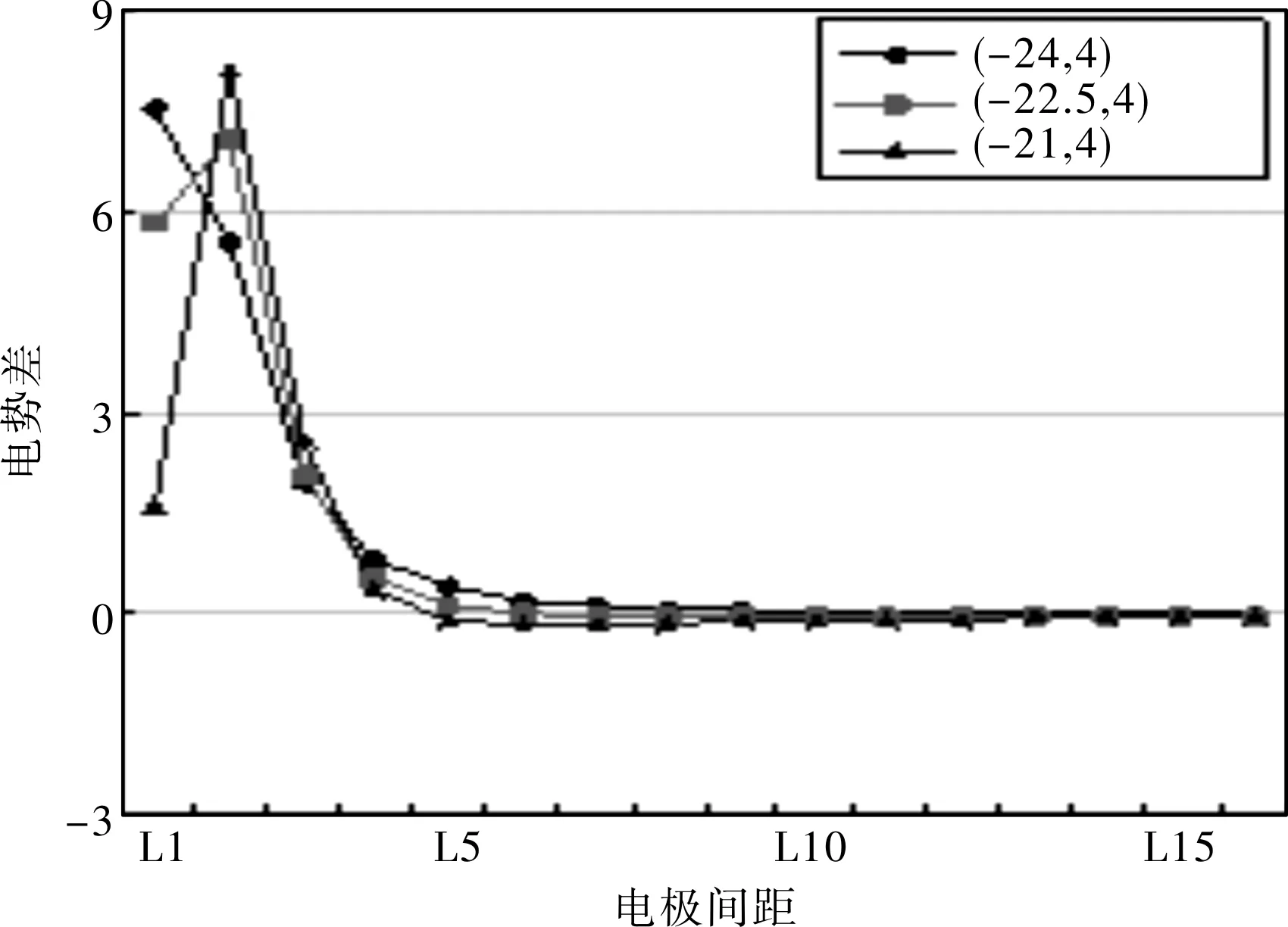
图5　圆心位于(-24,4),(-22.5,4),(-21,4)的相对电势差变化

由图4可知，相对电势差的最大值处(凸起)刚好对应圆心的近似位置，两者存在一一对应的关系。图5中出现了明显的凸起，由此也确定了小圆圆心的近似位置，所以相对电势差分析法要比绝对电势差分析法更完善，具有普遍性。

3.2确定半径大小方法对比

(1)绝对电势差分析法

分别设置小圆半径r为1 cm、2 cm、3 cm和4 cm，对应半径的电势差变化如图6所示。

由图6可知，小圆半径r越大，曲线凹陷幅度越大，所以可以通过凹陷幅度从整体上判断出半径的大概，并不够精确。

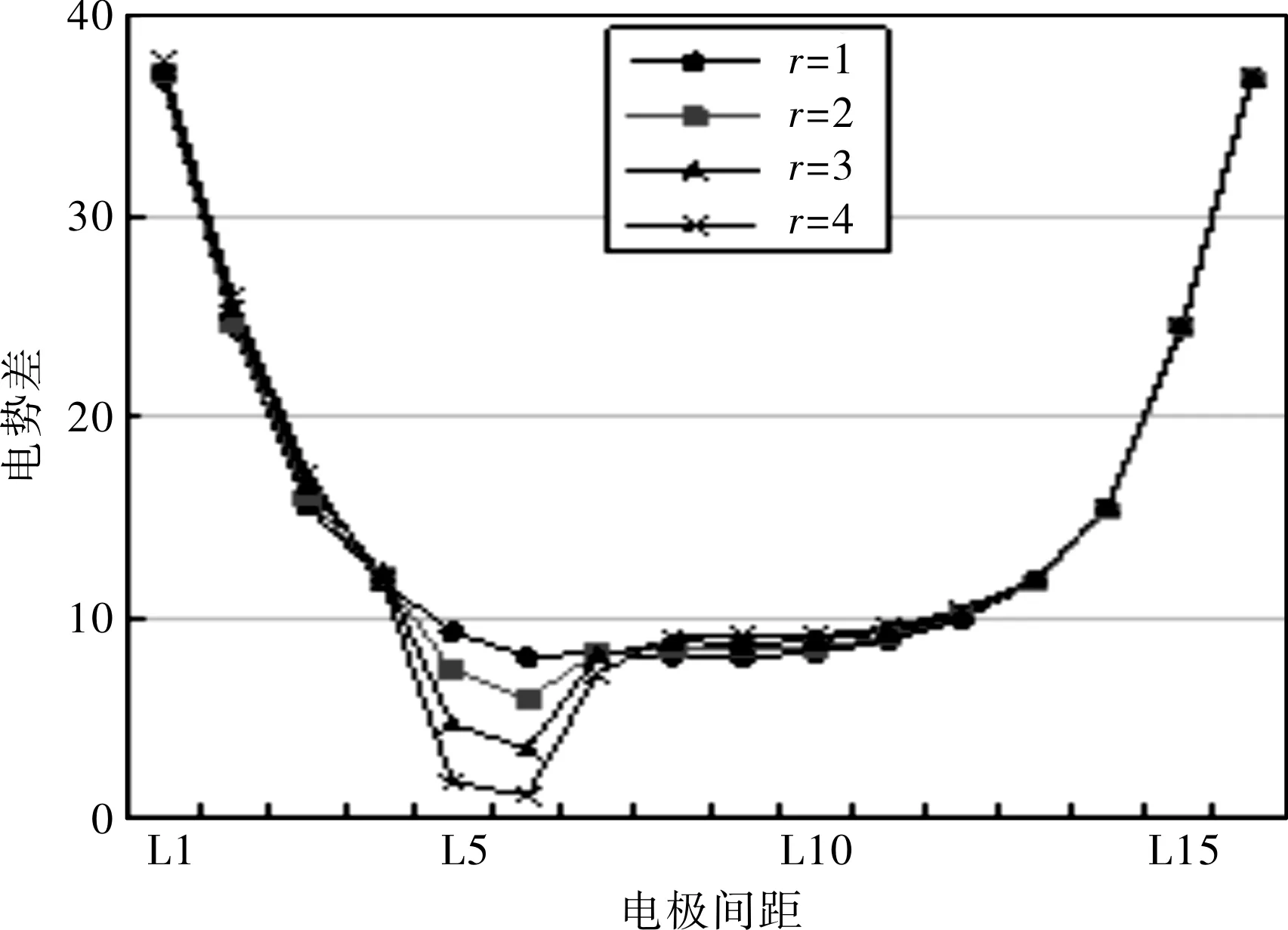
图6　不同半径大小的绝对电势差变化

(2) 二分法

设置小圆半径r未知，圆心(9,4)。不同半径的绝对电势差变化如图7所示。通过图6已经知道半径越大，凹陷幅度越大，所以图7中未知半径r是大于2 cm的，在半径r范围位于[2,4]之间，采用二分法取得r=3 cm，比较绝对电势差变化可知，未知半径小于3 cm，所以未知半径的范围在[2,3]，依此类推，直至确定半径大小。

图7　二分法下不同半径的绝对电势差变化

由上述分析可知，相对电势差分析法可以确定所有的圆心位置，比绝对电势差分析法更具普遍性。对于小圆半径大小的确定，绝对电势差分析法可以直观的得到半径的大概，但精度较差，而二分法可以得到一个精度范围以内的半径，精度较高。

4　结语

利用Comsol multiphysics构建开放式电阻抗成像的模型，通过绝对电势差、相对电势差和二分法，确定目标小圆圆心的近似位置和半径大小。对比结果表明，对于圆心近似位置的确定，采用相对电势差分析法更具普遍性；对于小圆半径的确定，采用二分法可以得到精度范围内的半径大小，具有较高的精度。

[1]袁全,杨道业,金月娇.电阻层析成像系统的设计[J/OL].仪器仪表与传感器,2016(5):1002-1841[2015-09-16]. http://www.cnki.net/KCMS/detail/detail.htm.

[2]常甜甜,魏雯婷,丛伟杰.电阻抗成像的稀疏重建算法[J/OL].西安邮电大学学报,2013,18(2)92-96[2016-02-12]. http://www.cnki. net/KCMS/detail/detail.htm. DOI:10.13682/J.issn. 2095-6533.2013.02.024.

[3]李昌兴,刘畅,常甜甜.基于电阻抗频谱的乳腺组织分类[J/OL].西安邮电大学学报,2015,20(6)98-101[2016-02-12]. http://www.cnki.net/KCMS/detail/detail.htm. DOI:10.13682//j.issn.2095-6533. 2015.06.021.

[4]王玥,刘丽炜,胡思怡,等.基于COMSOL Multiphysics对Cu2S量子点的表面等离激元共振模拟研究[J/OL].物理学报,2013,62(19): 477-482[2016-02-12]. http://dx.chinadoi.cn/10.7498/aps.62.197803.

[5]张亮,姚磊华,王迎东.基于COMSOL Multiphysics的三维地质建模方法[J/OL].煤田地质与勘探,2014,42(6):1001-1986[2014-06-03]. http://dx.chinadoi.cn/10.3969/j.issn.1001-1986.2014.06.003.

[6]唐化勇,牟永阁,杨常运，等.生物电阻抗成像技术在医学中的应用[J/OL].第四军医大学吉林军医学院学报,2000,22(3):174-176. http://dx.chinadoi.cn/10.3969/j.issn.1673-2995.2000.03.027.

[7]庄翠芳,阳波,牛俊泽.多频率激励生物电阻抗测量方法的研究[J/OL].计算机测量与控制,2016(6)1671-4598[2016-12-22]. http://www.cnki.net/KCMS/detail/detail.htm. DOI:10.16526/j.cnki.11-4762/tp.2016.05.021.

[8]何传红,何为,黄嵩,等.开放式电阻抗成像基本原理和仿真实验研究[J/OL].中国生物医学工程学报,2008,27(5):669-674[2016-02-12]. http://dx.chinadoi.cn/10.3969/j.issn.0258-8021.2008.05.007.

[9]饶水发,戎舟.基于ARM的32电极电阻抗成像系统设计[J/OL].计算机技术与发展,2016,26(6):138-141[2016-05-05]. http://dx.chinadoi.cn/10.3969/j.issn.1673-629X.2016.06.030.

[10]黄嵩,何为,罗辞勇.开放式电阻抗成像中变差正则化重构算法[J/OL].重庆大学学报,2011,34(10):1-7[2016-02-12]. http://www.cnki.net/KCMS/detail/detail.htm.[11] 何传红,何为,张莉,等.提高开放式电阻抗成像检测深度的方法研究[J/OL].系统仿真学报,2011,23(9):1990-1994[2016-02-12]. http://www.cnki.net/KCMS/detail/detail.htm. DOI:10.16182/j.cnki.joss.2011.09.021.

[12]范文茹,郝魁红,许燕斌.开放式电阻抗成像激励策略研究[J/OL].仪器仪表学报,2014,35(6):1269-1275[2016-02-12]. http://www.cnki.net/KCMS/detail/detail.htm.

[13]罗辞勇,何传红,何为.开放式电阻抗成像的灵敏度和病态性问题[J/OL].中国生物医学工程学报,2008,20(8):544-548[2016-02-12]. http://dx.chinadoi.cn/10.3969/j.issn.0258-8021.2009.04.011.

[14]刘斌,何为,张晓菊,等.开放式电阻抗断层成像测量系统设计与成像试验研究[J/OL].医疗卫生装备,2009,30(4):1003-8868[2016-02-12]. http://dx.chinadoi.cn/10.3969/j.issn.1003-8868.2009.04.001.

[责任编辑：祝剑]

Target localization based on open electrical impedance tomography

LIN Zhenxian1，CHENG Qingtao2，XI Xiaoqiang3

(1.School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2.School of Communications and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;3.Institute of Internet of Things and IT-based Industrialization, Xi’an University of Posts and Telecommunications, Xi’an 710061, China)

A localization methods based on open electrical Impedance tomography for the small round target location and size is presented in this paper. Comsol multiphysics tool is used to establish the model of open electrical impedance tomography. Electrode potentials for the center position with radius in different sizes are measured and recorded. Potential differences between adjacent electrode points are then calculated. The corresponding relation between the boundary potential difference and the center of the approximate location and the radius size are analyzed. The target is therefore located by the potential difference analysis method and the dichotomy. The results from comparative experiments show that relative potential difference analysis method can universally quickly determine the position of the small target, and that the dichotomy can accurately determine radius of small target with high accuracy.

open electrical impedance tomography, potential difference method, dichotomy

10.13682/j.issn.2095-6533.2016.05.006

2016-04-18

国家自然科学基金资助项目(11275099，11475135)

林椹尠(1969-)，女，博士，教授，从事小波理论研究。E-mail:lzhx126@126.com

程庆涛(1993-)，男，硕士研究生，研究方向为信号与信息处理。E-mail:1542779207@qq.com

O441

A

2095-6533(2016)05-0029-05