基于FAHP的功效系数法的岩质边坡稳定性分级
秦胜伍,曹荣国,李广杰,马中骏,吕江峰
(1.吉林大学 建设工程学院,吉林 长春 130000,2.吉林大学 地质调查研究院,吉林 长春 130000)
基于FAHP的功效系数法的岩质边坡稳定性分级
秦胜伍1,2,曹荣国1,李广杰1,2,马中骏1,吕江峰1
(1.吉林大学 建设工程学院,吉林 长春 130000,2.吉林大学 地质调查研究院,吉林 长春 130000)
针对岩质边坡稳定性评价的模糊性与多指标性特点,采用模糊层次分析法确定Ⅰ、Ⅱ级指标权重,提高了0.1~0.9标度法所确定权重的客观性并克服了单一性,且避免了同一对指标比较时的不一致性,量化了不连续性基础指标。引入功效系数法对不同类型的基础指标进行功效系数值归一化求解,结合功效系数值与Ⅰ、Ⅱ级指标权重向量计算得出总功效系数值,据总功效系数值大小划分稳定性级别。在模糊层次分析法基础上,运用功效系数法对永吉岩质边坡进行稳定性评价、分级的结果与实际调查情况相符。证明该方法对岩质边坡稳定性分级具有很好的适用性与可靠性。
模糊;层次分析法;功效系数法;岩质;边坡;稳定性分级
近年来,我国资源开发和基础设施建设不断发展,由此也引发了一系列地质灾害问题,其中岩质边坡受控因素比较复杂,失稳具有突发性,造成道路阻断、房屋被埋,给国民财产带来巨大损失[1]。对于历史数据充足、岩体力学参数易获得的岩质边坡,国内广泛采用岩体Q系统分类、岩体权值系统 RMR、边坡岩体评价系统SMR 和 CSMR 等方法对岩质边坡稳定性进行评价和分级[2-3]。但是对于历史数据匮乏,岩体力学参数不易获得的岩质边坡用现有的力学或数学的经典模型很难进行统一研究[4]。一般多采用传统层次分析法与其他方法结合的方法研究此类边坡,如鲁光银等[5]与杨阳等[6]分别采用层次分析法与改进层次分析法评价边坡稳定性;王新民等[7]则采用层次分析法与可拓模型相结合,利用物元概念,评价结果与RMR法和BQ法得到的结果有很好的一致性;赵建军等[8]采用因子分析法考虑边坡结构等主要因素重点讨论确定指标权重;张士伦等[9]采用模糊松散体理论评价了雅康高速岩质边坡稳定性。对于历史数据少、岩体力学参数不易获得的边坡,前人多根据边坡稳定性评价存在一定的不确定性、模糊性和层次性以及复杂性的特点,多采用了模糊数学理论与多指标评价层次分析的思想。每种方法都有优缺点,没有哪一种方法能得到十分准确的评价分级结果,因此探讨新的方法显得十分必要。
功效系数法用在企业管理、财务分析已经很成熟,在财务风险预警[10]、企业业绩评价[11]、医疗质量综合评价[12]等方面已经得到广泛应用,并且收到良好的效果。笔者根据前人既有的研究成果提出了基于层次分析法的功效系数法岩质边坡评价分级方法,并以永吉周边48个岩质边坡为计算实例,对本文提出的方法加以验证。
1 方法与基本原理介绍
1.1方法介绍
功效系数法又叫功效函数法,是指根据多目标规划的原理,把所要考核的各项指标按照多档次标准,通过功效函数转化为可以度量的评价分数,再经过加权平均进行综合评价,据以对被评价对象进行总体评价得分,从而评价被研究对象的综合状况的一种方法[13],其基本原理如下。[14-15]
(1) 选取指标
指标要求具有一定的普适性、代表性,真实地反映被评价对象的综合情况。其指标有四种类型即:区间型变量(以数值在某一确定的区间为标准)、稳定型变量(数值在某一时点为最佳)、极小型变量(越小越安全)和极大型变量(越大越合理)。
(2)确定满意值与不允许值
功效系法中的每一个评估指标都要有确定的不允许值(下限)和满意值,满意值与不允许值根据变量的类型而确定的,通常满意值即达到某一效果的经验值,不允许值即对某一效果可以接受的极值。
(3)确定单项功效系数
假设各指标的实际值为x,满意值为s,满意值的上限为sp,满意值的下限为sq,不允许值为n,不允许值上限为np,不允许值下限为nq。根据指标类型,单项功效系数分别有不同的确定函数Gint,Gsta,Gmin,Gmax。
(1)
(2)
(3)
(4)
(4)确定综合功效系数
根据以上求得单项功效系数值Gi,根据模糊层次分析法确定单指标的权重Wi,最终的总功效系数为:
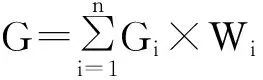
(5)
据总功效系数G对岩质边坡稳定性评价与分级。
在确定权重指标时,根据指标的类型采用模糊层次分析法确定权重。模糊层次分析法原理介绍如下:模糊层次分析法对层次分析法加以改进,是一种对定性问题进行定量分析的多准则决策方法,它将人对事物的认知强弱程度用模糊数来表示,从而,扩展了其适用范围。模糊层次分析法基本原理方法如下[16]:
(1)对于具体问题确定其论域,包括指标集B=[B1,B2,…Bn],评判集D=[D1,D2,…Dm],以及指标集D中的基础指标或子指标。
(2)通过论域建立层次结构模型,笔者对不连续指标采用德尔菲法,对连续性指标采用模糊数学中的隶属度函数方法,经查阅资料,根据实际情况采用文献[17]中的“降半梯形”公式。
(6)
(7)
(8)
(9)
(3)根据0.1~0.9标度法构造优先判断矩阵F=(fij)n×n,然后将优先判断矩阵转化为模糊一致判断矩阵。
R=(rij)n×n,rij=(ri-rj)/2n+0.5。
(10)
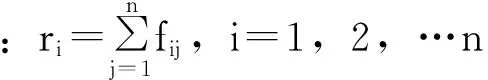
(11)
且模糊一致判断矩阵R具有如下性质rii=0.5,i=1,2,…n;rij=1-rji,i,j=1,2,…,n;rij=rik-rjk+0.5,i,j,k=1,2,…,n。
(4)一致性调整。即确定一个或几个最有把握的指标比较值,修改其他比较值,直到任意指定两行的对应元素之差为常数。
(5)矩阵转换权重计算。将调整后的模糊一致矩阵转化为互反判断矩阵
E=(eij)m×n,
(12)
其中:eij=rij/rji。
(13)
将权重向量W(0)作为初始向量V(0),利用公式
V(k+1)=EY(k),
Y(k)=V(k)/‖V(k)‖∞,k=1,2,…,
(14)
进行迭代。ε为规定误差。
‖V(k+1)‖∞-‖V(k)‖∞<ε。
(15)
则‖V(k+1)‖∞为最大特征值。最终权重向量W=(w1,w2,…,wn)T,即
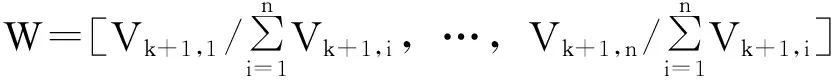
(16)
1.2方法的实现与应用
通过对该地区岩质边坡的地层岩性、地质构造、节理优势方向、植被覆盖情况、边坡排水情况、边坡开挖情况、岩体风化程度等方面调查。确定出一级分级指标与二级分级指标,并根据功效系数法的思想确定每项指标的满意值与不允许值,同时采用 0.1~ 0.9 标度法构造出各层次指标的优先判断矩阵,经模糊一致变换后再转化为互反判断矩阵,利用幂法公式计算得出指标权重向量。对各个指标综合评分,最后根据指标类型与其评价所得分值用公式(1)~(4)进行单项功效系数计算,结合单项系数值与各级指标权重计算每个边坡的总功效系数值,结果值的范围为0~100,然后根据总功效系数值与稳定级别对应值确定最终的岩质边坡稳定性级别。具体方法实现流程如图1所示。
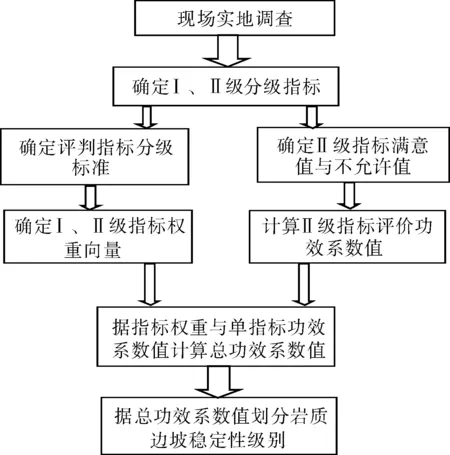
图1 方法应用流程图
2 岩质边坡分级的工程应用
2.1研究区概况
永吉县位于吉林省中东部,松花江上游,地处43°18′~43°53′N,125°48′~136°38′E之间。县城周边有大型露天钼矿,且采石场较多,岩质边坡绝大多数为人工边坡,分布多沿路两侧,人类活动较强烈。其组成主要为花岗闪长岩、次流纹岩、凝灰质砂岩等,多中强风化以上、节理发育、倾角较大、植被覆盖率较低。此地区夏季单次降雨量较大且分布不均,如2010年7月27日-28日,永吉县平均降雨量达120.7 mm,局部地区达254.9 mm。冬季气温较低、多雪、昼夜温大。
2.2指标选取与层次结构模型的确定
综合分析永吉工程地质、气象环境水文、工程施工因素并参考相关文献,确立其一级指标与二级指标及其评价分级。分级评价过程中没有考虑地震烈度,原因是在本地区地震烈度在同一水平,其对各个岩质边坡影响程度相同。根据工程地质条件、气象水文地质条件、工程施工条件确立一级指标集B={B1,B2,B3},根据工程地质条件中的子指标,即地质构造、岩体的岩性、岩体的风化程度、地形地貌确定B1={C1,…C5};根据气象环境水文地质条件子指标,即降雨强度、边坡排水情况、植被覆盖程度确定B2={C6,C7,C8},根据工程施工条件中子指标,即边坡开挖坡度、边坡开挖高度、边坡开挖方式确定B3={C9,C10,C11};根据岩质边坡稳定性级别,即稳定、基本稳定、不稳定、极不稳定建立评判集D={D1,D2,D3,D4}。综上,不连续性指标采用专家打分法,连续性指标采用公式(6)~(9)建立各级评价指标及其分级标准,如表1所示。
2.3确定指标权重向量
选用 0.1~0.9 标度法(表2)构造出各层次指标的优先判断矩阵,根据一级指标确定的优先判断矩阵如下:

(17)
将优先判断矩阵转化为模糊一致矩阵

(18)
W={0.3288,0.2687,0.4025}。
(19)
同理二级指标权重经计算如表3所示。
2.4确定满意值与不允许值
综合表1,对于连续性指标的满意值与不允许值为实际指标值,对于不连续模糊指标的满意值与不允许值为其分值,最终确定每个指标的满意值与不允许值(表4)。
2.5功效系数计算
(1)单项功效系数计算
据表4,地形地貌、降雨强度、开挖坡度、开挖高度采用极大型变量公式(4)计算,地质构造、岩体岩性、岩体风化程度、节理方向、边坡排水情况、植被覆盖率与开挖方式采用极小型变量公式(3)计算。
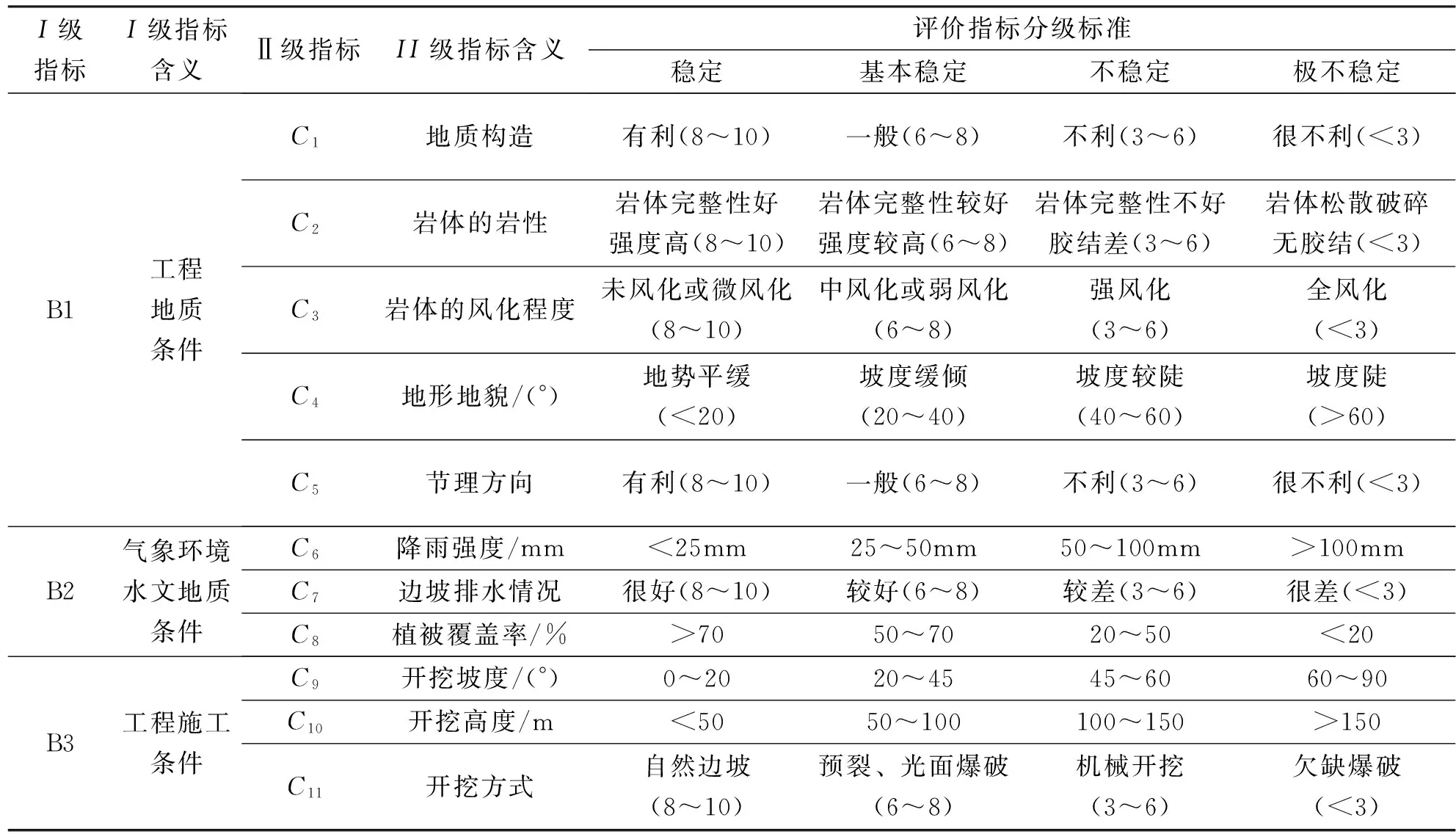
表1 各级评价指标及其分级标准[18-19]

表2 标度的意义
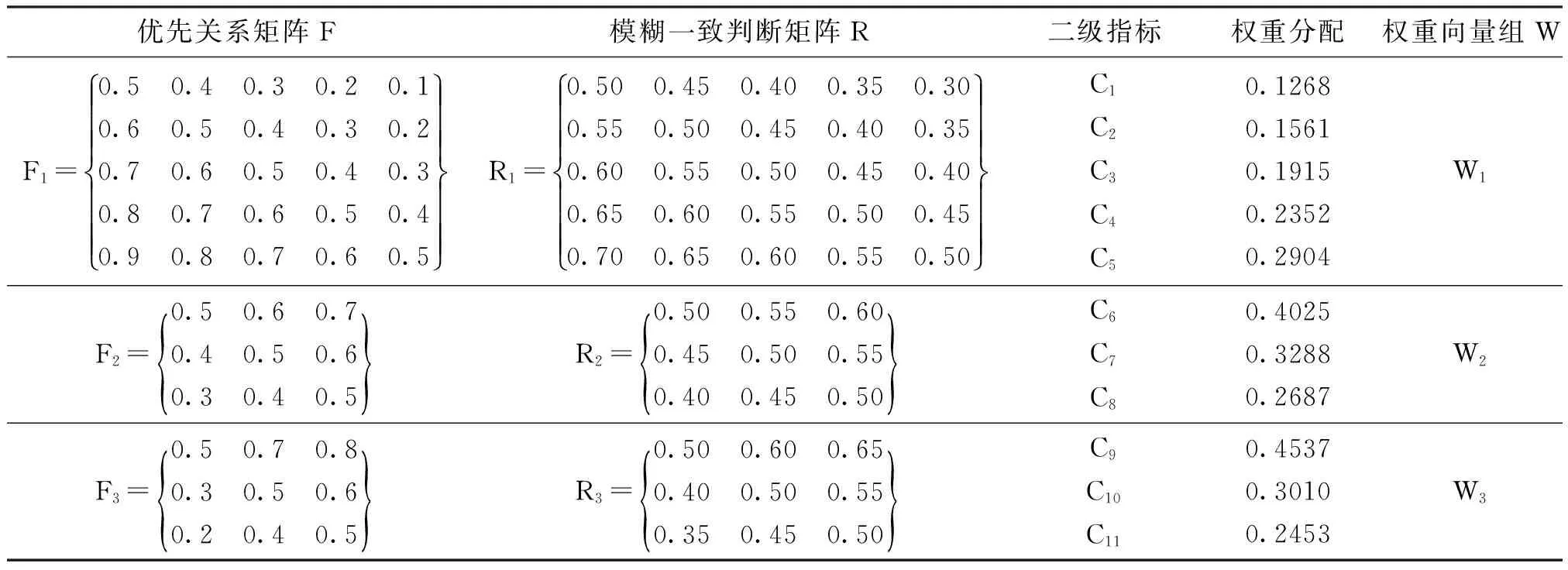
表3 二级指标权重

表4 基础指标的满意值与不允许值
(2)总功效系数计算
据表3,基础指标权重值经模糊层次分析法确定,根据单项功效系数值,利用公式(4)计算得出I级单个指标总功效系数值,再经公式(5)计算即得边坡稳定性的总功效系数值。总功效系数值与分级对照表如表5所示。

表5 总功效系数值与分级对照表

表6 单项指标评价与分级结果
2.6结果分析
笔者对永吉周边敖哈达山等48处岩质边坡通过matlab计算结果并分析得出:极不稳定边坡4处:敖哈达山斜坡、口前2号斜坡、D004斜坡、二道埠子不稳定斜坡;不稳定斜坡9处:东荣石场斜坡(图2)、口前1号、郭范斜坡、三合斜坡、猪咀砬子斜坡、小东山斜坡、暖家沟斜坡、泉眼头斜坡;基本稳定边坡车山弯等16处,稳定边坡兰旗屯车沟边坡等19处。部分评价结果如表6所示,从表6可以看出:对于Ⅳ级中的边坡,敖哈达山岩质边坡稳定性比口前2号更差一些。
图2为东荣石场不稳定斜坡,无不良地质现象、节理不发育,岩体完整性较好,岩体表面未风化,地形较陡、平均倾角60°,边坡排水情况好,植被覆盖率约3%,边坡开挖坡度82.1°,高度57.6m,开挖方式采用欠缺式爆破、岩体松动,最终评价的总功效系数值为78.989。其他岩质边坡各指标情况与评价结果见表6。

图2 东荣石场不稳定斜坡
3 结论
(1)模糊层次分析法采用构造模糊互补矩阵的方法,相较传统层次分析法,无需一致性检验,避免反复调整检验判断矩阵所带来的繁琐性与计算矩阵的不收敛,并采用了0.1~0.9标度法,克服了传统层次分析法对同一对指标比较时的不一致性。
(2)首次引入功效系数法用于岩质边坡的稳定性评价与分级,在综合考虑工程地质条件,气象、水文、环境地质条件与工程施工条件的影响指标的情况下,采用总功效系数值作为分级依据,所得出的功效系数值反映出了同一稳定级别的边坡稳定性优劣情况。
(3)在模糊层次分析法确定Ⅰ、Ⅱ级指标权重的基础上,运用功效系数法计算基础指标的单项功效系数值,并结合Ⅰ、Ⅱ级指标权重向量计算出总功效系数值。最后分级结果符合实际调查的岩质边坡稳定性分级情况。证明了功效系数法对岩质边坡评价分级的可行性与可靠性。
[1]罗书学,李龙起,徐骏,等. 高陡边坡运营安全防灾监控及报警系统技术研究科研报告[R].成都:西南交通大学岩土工程系,2012.
[2]许宏发, 陈锋, 王斌,等. 岩体分级BQ与RMR的关系及其力学参数估计[J].岩土工程学报, 2014, 36(1):195-198.
[3]刘帝旭,曹平.基于灰色系统理论的改进SMR法初探[J].岩土力学,2015(S1):136-151.
[4]徐卫亚,郑文棠,石安池.水利工程中的柱状节理岩体分类及质量评价[J].水利学报, 2011(3):262-270.
[5]鲁光银,朱自强,李华,等.公路隧道岩体质量分级的模糊层次分析法[J].中南大学学报(自然科学版), 2008,39(2):368-374.
[6]杨阳,尚文猛,肖超超,等.改进层次分析法在滑坡稳定性评价中的应用[J].武汉工程大学学报, 2015(8):13-19.
[7]王新民,康虔,秦健春,等.层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用[J]. 中南大学学报(自然科学版), 2013,44(6):2455-2462.
[8]赵建军,贺宇航,黄润秋,等.基于因子分析法的边坡稳定性评价指标权重[J].西南交通大学学报, 2015(2):325-330.
[9]张士伦,张孟喜,吉随旺,等.基于模糊分析的松散体边坡稳定性评价[J].上海交通大学学报,2015,49(7).1035-1039,1045.
[10]吴本杰.基于功效系数法的财务危机预警[J].价值工程, 2012, 31(2):143-144.
[11]王美荣.功效系数法在企业绩效评价中的应用[J].财会通讯, 2010(20):76-78.
[12]夏季明,孙爱峰.功效系数法在医疗质量综合评价及其变化发展趋势中的应用[J].中国医药指南,2010,8(20):346-347.
[13]王迎超,尚岳全,孙红月,等.基于功效系数法的岩爆烈度分级预测研究[J].岩土力学, 2010, 31(2):529-534.
[14]孟凡奇,李广杰,王庆兵,等.基于功效系数法的泥石流灾害预警研究[J].岩土力学,2012,33(3):835-840.
[15]陈丹.基于功效系数法的金融体系预警研究[D].石家庄:河北工业大学, 2014.
[16]张吉军.模糊层次分析法(FAHP)[J]. 模糊系统与数学, 2000, 14(2):80-88.
[17]刘小艳,刘欣宇,王梅.隶属函数的确定及应用[J].电脑知识与技术,2011,6(31):8831-8832.
[18]李建峰,万臣,赵勇.高寒高海拔地区岩质边坡稳定性评价研究[J].重庆交通大学学报(自然科学版),2015,34(2):45-49.
[19]袁尚南,强茂山,温祺,等.基于模糊层次分析法的建设项目组织效能评价模型[J].清华大学学报,2015,55(6):616-623.
Stability Classification of Rock Slope Based on FAHP Efficiency Coefficient Method
QIN Shengwu1, 2, CAO Rongguo1, LI Guangjie1, 2, MA Zhongjun1and LV Jiangfeng1
(1.SchoolofConstructionEngineering,JilinUniversity,Changchun130000,China;2.GeologicalSurveyResearchInstitute,JilinUniversity,Changchun130000,China)
Accordingtothecharacteristicsoffuzzyevaluationofrockslopestabilityandmultiindex,usingfuzzyAHPtodeterminetheweightofthefirstandsecondlevelindicators,weimprove0.1-0.9scalemethodofindexweightandsubjectivityandovercomethesingularity,andavoidtheinconsistencyofthesameindextoquantifythediscontinuitybasedindex.Theefficacycoefficientmethodisintroducedtosolvethenumericalnormalizationmethodfordifferenttypesofbasicindexes.Thetotaleffectiscalculatedwiththenumericalefficiencyofthenumericalsimulationandthefirstandsecondlevelindexweightvector,accordingtothegeneralefficacycoefficientsizestabilitylevel.OnthebasisofFuzzyAHP,theresultsofstabilityevaluationandclassificationofrockslopeinYongjicorrespondtotheactualsituation,whichprovedthatthemethodhasgoodapplicabilityandreliabilityforthestabilityclassificationofrockslope.
fuzzy;AHP;efficacycoefficientmethod;rock;slope;stabilityclassification
2016-03-21
2016-05-13
国家自然科学基金青年基金(41202197);国土资源部公益性行业科研专项(201211095-6);吉林省永吉县1:5万地质灾害调查与区划项目
秦胜伍(1980-),男,吉林长春人,博士,副教授,主要从事地质灾害调查,工程地质方面研究工作.
E-mail:qinsw@jlu.edu.cn
TU 443 ;X43
A
1000-811X(2016)04-0027-06
10.3969/j.issn.1000-811X.2016.04.005
秦胜伍,曹荣国,李广杰,等. 基于FAHP的功效系数法的岩质边坡稳定性分级[J].灾害学,2016,31(4):27-32.[QIN Shengwu,CAO Rongguo,LI Guangjie, et al. Stability Classification of Rock Slope Based on FAHP Efficiency Coefficient Method[J].Journal of Catastrophology,2016,31(4):27-32.doi: 10.3969/j.issn.1000-811X.2016.04.005.]

