载液铁路罐车超速连挂冲击过程研究*
林建军, 姚曙光, 邓 浩
(1 中南大学交通运输工程学院 轨道交通安全教育部重点实验室, 湖南长沙 410075;2 武汉地铁集团有限公司, 湖北武汉 430030)
专题研究
载液铁路罐车超速连挂冲击过程研究*
林建军1, 姚曙光1, 邓浩2
(1中南大学交通运输工程学院轨道交通安全教育部重点实验室, 湖南长沙 410075;2武汉地铁集团有限公司, 湖北武汉 430030)
为了研究载液铁路罐车超速连挂的冲击过程,采用拉格朗日算法和任意拉格朗日-欧拉(ALE)算法建立起载液罐车的有限元模型,采用罚函数约束算法实现罐体结构与液体的流固耦合作用,完成了对载液罐车超速连挂过程的数值模拟,分析了冲击过程中罐内液体的晃动以及罐体结构的力学响应。结果表明:以8 km/h超速连挂时,罐车撞击端第2个人孔附近发生微小变形,但其整体结构未受到破坏;冲击过程引起了罐内液体的剧烈晃动,罐体局部应力较大是液体晃动与纵向冲击力共同作用的结果;人孔附近以及上、下罐板连接处属于罐体结构的薄弱部位;为减缓冲击过程中罐内液体的剧烈晃动,有必要在罐体内部加装防波板结构。
载液罐车; ALE算法; 超速连挂; 液体晃动
目前,我国编组站货车允许的安全连挂速度规定为5 km/h,而实际作业中货车超速连挂情况突出,赵琨等人调研发现超速连挂均在8 km/h左右[1-2]。超速连挂产生的冲击作用可能会超出钩缓装置的承载能力,容易引起载液罐车内部液体的剧烈晃动,液体的剧烈晃动反过来又会作用于罐体结构,这种交互作用严重时会引起罐体局部结构的塑性变形,对货物的运输安全造成威胁。
国内外许多学者对储液容器的碰撞冲击问题做过研究,但主要针对形状简单的贮箱结构[3],对载液铁路罐车这样大型储液结构的冲击问题少有研究。李政等人[4]采用ALE有限元法对双层储液容器的跌落碰撞问题进行了研究,分析了碰撞过程中容器的力学行为以及液体的变形行为;杨书仪等人[5]运用LS-DYNA研究了贮液塑料容器的跌落问题,分析了跌落角度等对容器跌落冲击应力的影响;Marco Anghileri等人[6]采用ALE等不同算法对载液水箱跌落进行研究,发现ALE算法能定性地反映试验结果;Ainian Zhang等人[7]对载液油轮与集装箱船的碰撞进行了数值模拟,比较了ALE算法、拉格朗日算法等在模拟碰撞时的差异,发现采用ALE算法计算结果更合理,且节省计算时间。基于拉格朗日算法建立罐体结构的有限元模型,基于ALE算法建立罐内液体及空物质层的模型,研究了罐车8km/h超速连挂冲击过程中罐内液体的晃动、罐体结构的力学响应以及两者的内在联系,发现了罐体结构的薄弱位置,以期为提高铁路罐车的安全连挂速度提供理论参考。
1 计算模型的建立
采用Hypermesh建立了G70型载液轻油罐车的有限元模型,采用ANSYS/LS-DYNA对载液罐车连挂冲击过程进行仿真计算。载液罐车冲击连挂过程中罐车结构会产生复杂的力学响应,罐内液体与罐车结构之间存在典型的流固耦合作用。考虑带有同种缓冲器的载液罐车之间的连挂,重点研究超速连挂时罐内液体的晃动以及罐体结构的力学响应,由于连挂过程中的吸能主要体现在缓冲器上,因此将连挂冲击简化为带有两个缓冲器的罐车撞击固定刚性壁。
1.1ALE有限元法
LS-DYNA程序具有拉格朗日、欧拉和ALE 3种算法[8],基于ALE算法建立罐内液体及空物质层的模型。结构变形过于巨大时,拉格朗日算法可能引起网格畸变,造成仿真计算困难甚至中断。欧拉算法存在结构边界难以处理的问题,同时为了完全包含材料可能的运动范围,常有计算模型庞大,计算时间漫长等问题。ALE算法则结合了其他两种算法的优点[9],一方面材料可以在网格中流动,能够跟踪物质结构的边界运动,另一方面网格也可以随材料的流动而移动和变形,可以有效控制计算规模。
计算过程中,ALE算法先按照拉格朗日时步进行计算,于是单元网格随材料流动而产生变形,然后再按照ALE时步进行计算[10]:第1步,保持变形后物体的边界条件,重新离散边界内的单元,保持网格的拓扑关系不变;第2步,将变形网格中能量、密度、应力张量等单元变量和节点速度矢量等输送到离散后的新网格中[11]。
1.2流固耦合算法设置
通过定义状态方程来描述罐内液体压力和初始体积内能间的关系,这里选用线性状态方程:
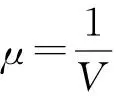
X1=2 190MPa,X2=9 224MPa,X3=8 767MPa,
Y1=4.934×10-7,Y2=13.937×10-7,Y3=0,
E=0.205 9mJ/mm3
选用无侵蚀的罚函数耦合方式来实现罐内液体和罐车结构的相互作用,这样既能保持计算的稳定性,又能够保证耦合计算过程中的能量守恒[13]。如图1所示,在流体物质点穿过结构单元的时候,计算分析流体与结构物质点的相对位移,并以此为依据,对结构和流体分别施加相应的节点力[14]。此外,为了避免搜索不到穿过结构单元的流体质点,可以考虑在结构单元上面增加适当的耦合点[15]。
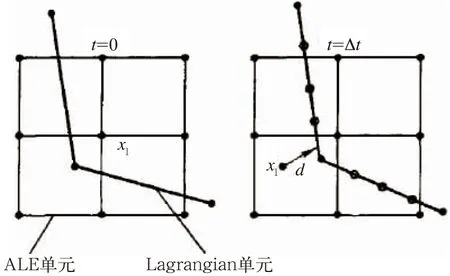
图1 罚函数耦合算法
1.3罐车结构模型
铁路罐车选用G70型轻油罐车,主要由罐体、转向架、钩缓装置、牵枕装置等部分组成。结构特点为牵枕装置与罐体组焊成无中梁结构,这有利于增大罐体直径。罐体是由上罐板、下罐板与封头组焊在一起的直筒式结构,材料为09Mn2低合金钢板,屈服极限295 MPa。选取MT-3型缓冲器,设定吸能量为37 kJ。取《铁路危险货物运输管理规则》中关于柴油准装最大高度的90%设定液面高度2330 mm,对应柴油总重53.23 t也满足规定要求。
建模时采用弹簧单元模拟钩缓装置,适当简化转向架结构。计算模型考虑轮轨间的摩擦,罐内液体采用实体单元建模,罐体及转向架等结构采用壳单元建模。罐内液体选用单物质的ALE算法模拟,在液体外面建一层空白的实体ALE网格,以给定液体物质足够的运动空间,并定义由质量加权的平均速度来控制ALE网格的运动。取单元尺寸为60 mm,为了防止流体渗漏,控制流体和结构单元尺寸比例为1:1。罐车计算模型如图2所示,整个计算模型包含SHELL163单元77 650个,SOLID164单元497 788个,节点585 799个。

图2 罐车有限元模型
2 计算结果分析
选取超速连挂冲击速度为8 km/h,采用LS-DYNA软件对冲击过程进行数值计算,从罐车运动速度变化、撞击力变化、罐内液体涌动以及罐体结构应力应变等几个方面进行详细分析,并联系各个方面的变化,寻找液体晃动与罐体结构力学响应的内在联系。
2.1罐车速度变化
首先分析连挂时罐车车体的速度变化。如图3所示,零时刻开始载液罐车以8 km/h的速度连挂冲击,在缓冲器的作用下车体速度迅速减小,100 ms减为零后车体开始反弹,液体向前涌动的惯性效应和钩缓装置的回弹反力互相作用使得罐车反弹结束后又向前运动,在不断地往复振荡后,800 ms以后罐车车体速度基本为零,由此判断罐车连挂冲击过程基本结束。冲击过程中的能量转换主要发生在载液罐车的动能与罐内液体、钩缓装置储存在势能之间,能量耗散主要由钩缓装置吸能以及摩擦耗能等完成。整个冲击过程遵循能量守恒定律,分析全过程的能量变化可知,总能量前后变化小于4%,可知计算较为稳定。

图3 车体速度变化
2.2撞击力变化
连挂冲击过程中撞击力变化如图4所示,冲击开始后钩缓装置短时间内快速受压变形,撞击力急剧增加,对应罐车车体的速度变化可以看出,100 ms罐车速度降为零时,两钩缓装置压缩量达到最大,最大为142.28 mm,撞击力增加到1.287 MN,随后随着车体的反弹,钩缓装置迅速卸载,撞击力快速减小。此后由于液体货物涌动带动罐车向前运动,钩缓装置多次加载又卸载,撞击力出现几个波动,但峰值力逐渐减小。整个过程中最大撞击力小于货车结构允许的最大纵向力2.25 MN,满足我国《车辆强度设计规范》中的要求。
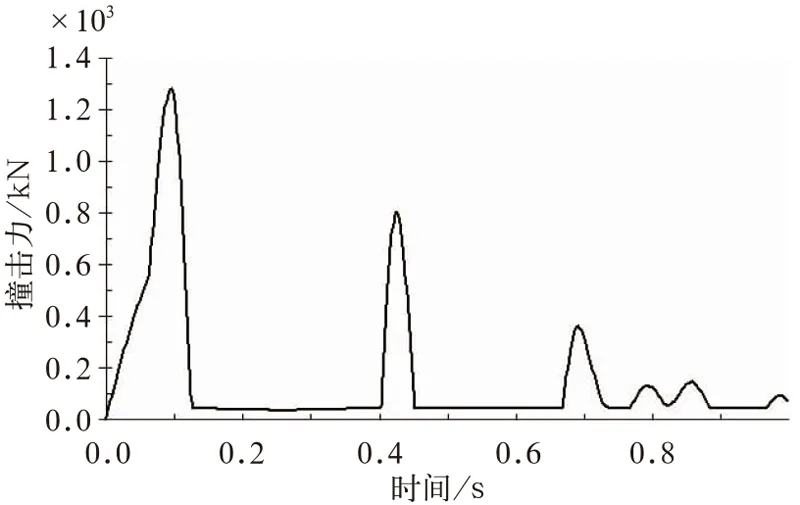
图4 撞击力变化
2.3罐内液体涌动
查看运动罐车内部液体在连挂冲击过程中特殊时刻的晃动情况,分析液体晃动与撞击力变化的内在联系,各特殊时刻点的液体晃动情形如图5所示。

图5 不同时刻液体变形
撞击开始后罐车减速,罐内液体保持原有的速度向前运动,86 ms罐内液体因封头约束而开始上涌,196 ms液体上涌至罐体顶部,液体向前涌动的惯性效应强于钩缓装置的回弹力,使得罐车逐渐停止回弹并再次向前运动,压缩钩缓装置,撞击力在400 ms开始再次上升,426 ms达到808 kN之后液体的回涌又引起钩缓装置卸载。综合以上分析可知,罐内液体的涌动与冲击过程中车体速度变化以及撞击力的变化有较好的一致性。
2.4罐体压力变化
分析冲击连挂过程中罐体的最大压力,发现520 ms罐体最大压力为163.5 MPa,出现在冲击端第2个人孔附近,如图6所示。罐体压力主要来自罐内液体对罐体结构力的作用,连挂冲击发生后,罐体的运动状态瞬间改变,罐内液体随之涌动,对罐体的力的作用效果也随即变化,罐体最大压力变化曲线如图7所示。

图6 罐体压力云图
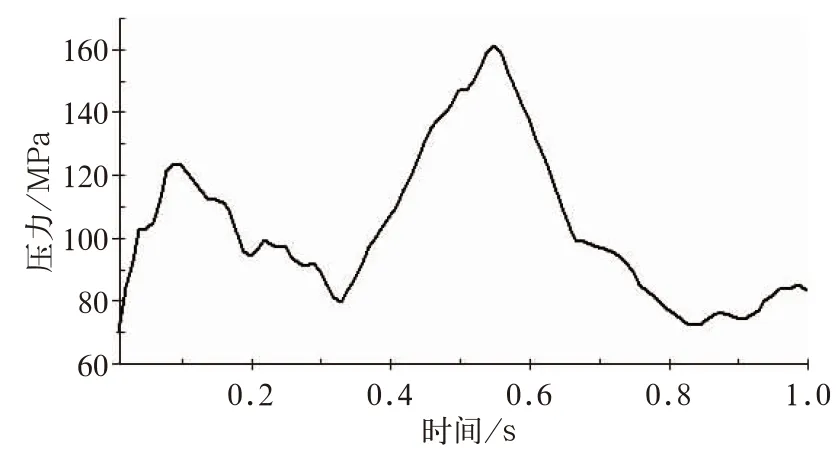
图7 罐体最大压力变化
2.5罐车应力应变
载液罐车连挂冲击过程中,罐内液体晃动与纵向冲击力综合作用可能会引起罐体局部结构应力较大,严重时会造成结构的塑性变形。考察罐体应力,发现520 ms罐体最大应力303.2 MPa,略大于材料的屈服极限295 MPa,发生在人孔与上罐板的连接处,如图8(a)所示,与该时刻罐体最大压力处在同一位置。同时发现450 ms上罐板和下罐板的连接处出现较大应力,如图8(b),这些部位均为连挂冲击过程中下罐车结构的薄弱位置。

图8 罐体等效应力云图
分析罐体最大应力随时间变化情况,如图9所示,520 ms最大应力303.2 MPa,该时刻前后共有60 ms超出了材料的屈服强度295 MPa。联系撞击力的变化可知,520 ms在液体涌动所引起的第2个撞击力峰值以后,罐内液体已充满罐体前端,晃动到第2个人孔处,如图10所示。结合罐体最大压力变化可以看出,两者的变化趋势整体一致,说明罐内液体晃动对罐体应力变化有直接的贡献作用,罐体局部应力较大是内部液体晃动和纵向冲击力共同作用的结果。
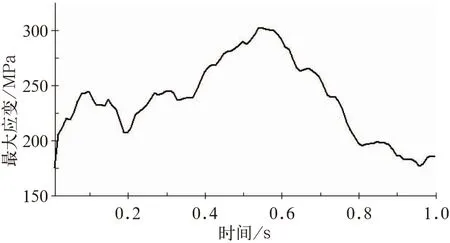
图9 罐体最大应力变化曲线

图10 液体晃动
塑性应变可以直接反映出罐车在超速连挂过程中的破坏情况,且随着冲击过程的进行,罐车的塑性应变是一个不断变化的过程。从罐车的速度变化可知,0.8 s冲击过程基本结束。查看0.8 s时刻罐车的塑性应变,如图11所示,罐车塑性应变最大值出现在撞击端第2个人孔与上罐板的连接处,最大值为0.006 3。说明载液罐车在8 km/h超速连挂引起了局部的微小变形,但未对车辆整体造成破坏。
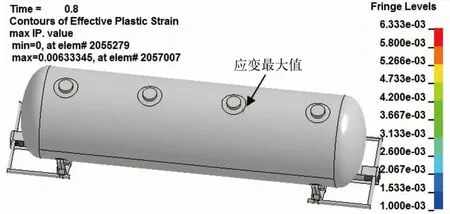
图11 罐车塑性应变
3 结 论
(1)载液罐车8 km/h超速连挂冲击,引起了撞击端第2个人孔附近的微小变形,但未对车辆整体造成破坏。冲击过程中产生最大应力303.2 MPa,罐体最大应力有60 ms超过了材料的屈服强度。
(2)冲击过程引起了罐内液体的剧烈晃动,冲击到了罐体顶部人孔,液体晃动对罐体应力变化有直接的贡献作用,罐体局部应力较大是液体晃动和纵向冲击力共同作用的结果。
(3)罐体人孔与上罐板的连接处以及上、下罐板的连接位置属于罐体结构的薄弱部位,为进一步提高罐车的安全连挂速度,需着重加强这些部位的连接强度。
(4)为减缓载液罐车超速连挂时罐内液体的剧烈晃动,有必要在罐体内部加装防波板结构。
[1]张红亮,杨浩,张超,等. 驼峰车组溜放的动态出口定速模型研究[J]. 交通运输系统工程与信息,2010,10(4):161-165.
[2]赵锟. 沈阳铁路局自动化驼峰作业安全性问题研究[D]. 成都:西南交通大学,2008.
[3]何华,田红旗,江帆. 铁路罐车液体运输动侧压力数值分析[J]. 铁道学报,2008,30(3):110-113.
[4]李政,金先龙,陈向东. 双层储液容器碰撞冲击的计算[J]. 机械工程学报,2008,44(10):216-221.
[5]杨书仪,赵继云,刘德顺,等. 贮液容器跌落冲击的有限元数值模拟研究[J]. 中国机械工程,2009,20(1):44-47.
[6]Marco Anghileri, Luigi M.L.Castelletti, Maurizio Tirelli. Fluid-structure interaction of water filled tanks during the impact with the ground[J]. International Journal of Impact Engineering, 2005, 31: 235-254.
[7]Ainian Zhang, Katsuyuki Suzuki. A comparative study of numerical simulations for fluid-structure interaction of liquid-filled tank during ship collision[J]. Ocean Engineering, 2007,(34):645-652.
[8]谢姣. 基于Ansys/ls-dyna数值模拟的爆破地震效应影响因素分析[D]. 西安:长安大学,2014.
[9]姚曙光. 铁路重载货车结构分析方法研究[D].长沙:中南大学,2010.
[10]邓浩. G70改型轻油罐车耐撞性能研究[D]. 长沙:中南大学,2014.
[11]陈向东,金先龙,李政. 波浪作用下软体浮囊动态响应仿真方法研究[J]. 系统仿真学报,2007,19(20):4616-4619.
[12]Y.S.Shin, M.Lee, K.Y.Lam, et. Modeling mitigation effects of water shield on shock waves[J]. Shock and Vibration, 1998, 5(4):225-234.
[13]李政,金先龙,陈向东. 储液容器跌落碰撞的并行仿真计算研究[J]. 应用基础与工程科学学报,2008,16(4):588-595.
[14]王惠,张会生. 柔性贮液容器跌落碰撞过程的三维数值模拟[J]. 噪声与振动控制,2009,(2):46-50.
[15]李政,金先龙,陈向东. 柔性储液容器跌落碰撞方法研究[J]. 振动与冲击,2007,26(8):72-75.
Research on the Impact Process of Heavy Tank Car Over-speed Coupling
LINJianjun1,YAOShuguang1,DENGHao2
(1Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic and Transportation Engineering, Central South University, Changsha 410075 Hunan, China; 2Wuhan Metro Grope Co. Ltd., Wuhan 430030 Hubei, China)
In order to study the impact process of heavy tank car over-speed coupling, the finite model of the heavy tank car was built adopting Lagrangian method and Arbitrary Lagrangian-Euler (ALE) method. The fluid-structure interaction between tank structure and liquid was realized by the constrained algorithm of penalty function. The over-speed coupling process of the heavy tank car was simulated, meanwhile the liquid sloshing and the mechanical response of the tank structure was analyzed during the impact process. The results illustrate that when the over-speed coupling takes place at 8km/h, small deformation occurs near the manhole of the tank car, but its whole structure is not damaged. The impact process causes severe liquid sloshing in the tank and the local large stress of the tank body results from the interaction of liquid sloshing and longitudinal impact. Places near the tank manhole and the junction between the upper and lower tank shells are the weak parts of the tank structure. In order to slow down the severe liquid sloshing in the tank during the impact process, it is necessary to equip the tank car with swash plate in it.
heavy tank car; ALE method; over-speed coupling; liquid sloshing
1008-7842 (2016) 04-0017-05
��)男,硕士研究生(
2016-03-17)
U272.4
Adoi:10.3969/j.issn.1008-7842.2016.04.04
*高铁联合基金资助项目(U1334208);教育部科学技术研究资助项目(113051A)

