图像数据的混沌模式的提取与表达*

于　硕，李思思，于万波

(1. 大连财经学院 工商管理学院，辽宁 大连 116600；2. 大连大学 信息工程学院，辽宁 大连 116622)



图像数据的混沌模式的提取与表达*

于硕1，李思思1，于万波2

(1. 大连财经学院 工商管理学院，辽宁 大连 116600；2. 大连大学 信息工程学院，辽宁 大连 116622)

研究以离散余弦变换(DCT)基函数作为辅助函数，结合序列灰度图像构造动力系统，然后迭代得到轨迹点集合(近似的吸引子)；使用该吸引子能够将视频图像的不同场景鉴别出来，用于视频分段裁剪等。使用多个DCT基函数矩阵，分别与一个图像构造动力系统，生成多个近似吸引子，这些吸引子可以作为图像的特征，用于图像识别，也可以重构原图像。

图像数据；混沌吸引子；离散余弦变换基函数

引用格式：于硕，李思思，于万波. 图像数据的混沌模式的提取与表达[J].微型机与应用，2016,35(18)：39-41，44.

0　引言

目前，大数据是许多学科领域的研究焦点[1-3]。大数据细节较多且无规则，不易用现有的数学方法、计算机工具等进行描述和处理[4-6]。混沌现象是非线性科学固有的、内在的、普遍的现象，尽管有些研究人员认为混沌是未来数据处理与表达的合适的工具，但是，目前把混沌理论与方法用到大数据处理与表达等并不多见。

图像数据是大数据的一种，具有可视性、复杂性、冗余性、规则性、随机性、人脑的可理解性等诸多特点[1,4-6]。对图像的理解、基于知识的存储、基于内容的检索、视频数据分析等还有很多问题有待解决。对于是否可以用混沌理论与方法处理图像、识别图像，查找相关文献发现了一些这方面的工作，例如LEE C S与ELGAMMAT A用非线性模型来表示人脸等[7-8]。基于非线性理论的方法作为一种新的特征表达方式，也已经开始初步应用于图像研究领域。

[9]、[10]的研究结果显示，以类似于文献[9]、[10]中的函数作为辅助函数，与其他(要处理的)函数或者矩阵构造动力系统，迭代后就可以产生(近似的)混沌吸引子，该吸引子形状随着动力系统参数的改变而改变，被处理函数的改变(图像形状)越小，其吸引子的轮廓形状改变就越小。基于此，文献[11]、[12]将正弦函数作为辅助函数，图像作为被处理函数，构造动力系统，迭代后得到的吸引子作为图像特征，继而用这种方法提取人脸图像特征，识别人脸，取得了较好的结果。

在参考文献[13]中，使用离散余弦变换(DCT)基函数矩阵作为辅助函数，将图像作为被处理函数，提取吸引子作为图像特征。因为DCT基函数更加震荡，具有更好的混沌特性，所以生成吸引子的质量更好。又因为DCT基函数数量众多，有更多的选择，所以，与正弦函数等相比，更适合于作为辅助函数。本文研究使用DCT基函数矩阵作为辅助函数，与视频图像构造动力系统，发现不同场景得到的吸引子不同，同时发现，使用多个吸引子可以重构图像。

下文中提到的吸引子都是指近似的混沌吸引子，或者说是动力系统的迭代轨迹。

1　动力系统构造与迭代方法

下面使用DCT基函数矩阵与图像矩阵构造动力系统。DCT基函数矩阵的定义如下：

(1)

其中, 0≤p≤M-1,0≤q≤N-1，

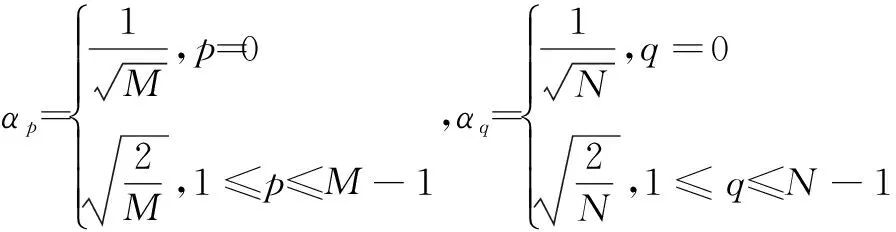
固定p,q后, R(m,n)都可以看作是以m,n为自变量的二元离散函数。这里令m,n,p,q均为正整数。随着p,q的变化, 基函数(矩阵)也随之变化, 共M×N个，选取一个，与灰度图像矩阵构造动力系统，如式(2)所示：

(2)

式(2)中，f(x,y)表示离散余弦基函数矩阵，g(x,y)表示灰度图像矩阵。

算法1利用DCT基函数与图像构造动力系统，然后迭代，生成迭代序列

(1)给定p,q的值以及M，N的值，此处取M=N=256。

(2)计算DCT基函数矩阵A，并用插值方法将其元素值调整到1～256之间。

(3)读入图像，适当裁剪边缘，以便生成质量更好的吸引子。

(4)将裁剪后的图像调整到M×N大小，记为H；将图像调整为1～256大小是为了使其与像素值一致，便于下面的迭代操作。

(5)给定初始迭代值(u,v)，代入矩阵B，即把(u,v)作为下标，取出矩阵B在(u,v)的元素值，记为z1；再将初始迭代值(u,v)代入矩阵H，即把(u,v)作为下标，取出矩阵H在(u,v)的元素值，记为z2。

(6)将(z1,z2)的值赋值给(u,v)，将每次的(z1,z2)记载下来，然后转到步骤(5)。

(7)将第(6)步重复执行n次。

2　视频图像特征提取

例如，使用DCT基函数作为辅助函数，对一视频图像进行处理，即按照一定时间间隔从视频图像中取出图像，与DCT基函数构成动力系统，使用算法1，迭代生成吸引子，不同场景下的视频图像其吸引子区别也比较大，如图1所示。

图1　不同视频场景下的图像吸引子

图1中的图像取自于一段视频。一般情况下，越复杂的图像，越容易产生吸引子。

算法2视频图像场景变化检测

(1)给定p,q的值，给定M，N的值，生成基函数矩阵A，将矩阵A的值调整为1～M，此处M、N的值视图像而定，例如M为每帧图像的高，N为宽。

(2)读入视频图像的三帧，转变为灰度图像，将图像的灰度值调整为1～N，记做B；分别与矩阵A构成动力系统，迭代生成近似吸引子，记做T1、T2、T3。

(3)将T1、T2、T3进行二维傅里叶变换，得到变换后的矩阵F1、F2、F3。

(4)计算F1、F2的相关系数，记为C1；再计算F2、F3的相关系数，记为C2。

(5)计算C1与C2差值绝对值D1，C2与C3的差值绝对值D2。

(6)如果D1远小于D2，那么T1、T2场景相同，T2、T3场景不同；如果D1与D2的差值较小，那么T1、T2、T3场景相同。

3　图像的分解与重构

下面使用多个DCT基函数矩阵，分别与一个图像构造动力系统，生成多个近似吸引子，然后再使用这些吸引子，重构原图像。

以Lena图像作为被处理函数，为了便于分析，对Lena图像进行了截取；与256×256的DCT基函数矩阵构造动力系统，p,q的值分别为(2,2)、(3,3)、(4,4)、(5,5)、(6,6)、(7,7)，使用算法1，得到的近似吸引子点阵如图2所示。

DCT基函数矩阵M=256,N=256, (p,q) 的值分别为(2,2),(3,3),(4,4),(5,5),(6,6), (7,7),图像使用Lena图像图2　近似吸引子点阵

吸引子用二维点集的形式表现，但是如果记录下这些点的先后顺序，便可以表达(记载)图像的灰度信息。图3

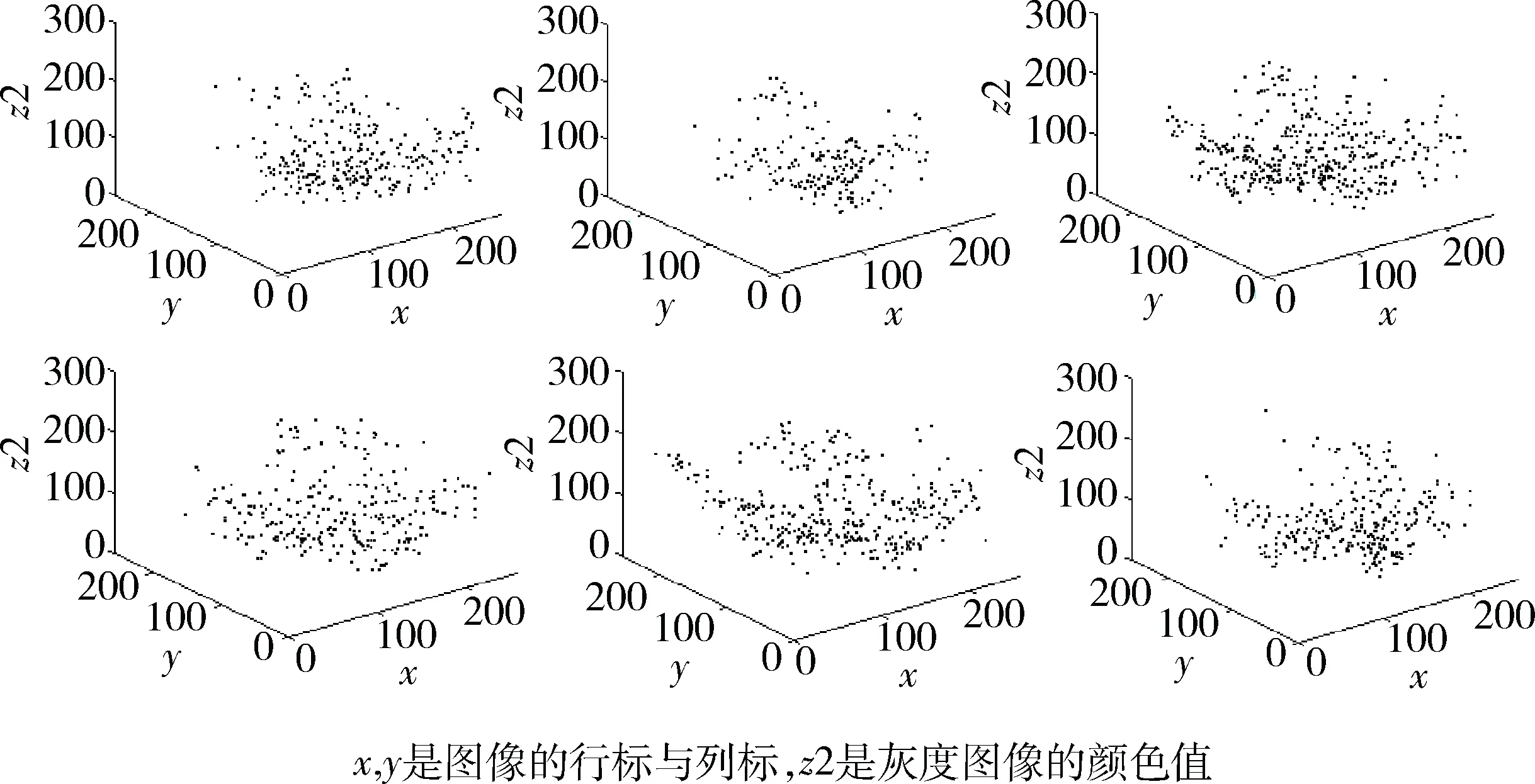
图3　吸引子点阵的三维显示

就是根据吸引子点产生的先后顺序，将二维吸引子转化为三维点阵；(x,y)是图像的像素位置，z轴是图像的灰度值。这些位置与灰度值来源于图像，可以表达图像的某种特征，也可以近似复原图像。

利用图3所示的吸引子三维点阵，可以近似复原图像。例如，使用语句forp=1 to 2, forq=1 to 2，嵌套循环，即利用(p,q)为(1,1)，(1,2)，(2,1)，(2,2)这4个DCT基函数矩阵，复原后效果如图4(a)所示；利用forp=1 to 5, forq=1 to 5嵌套循环，得到25个DCT基函数矩阵，复原效果如图4(b)所示；利用10×10=100个吸引子复原效果如图4(c)所示；利用15×15,30×30,40×40个吸引子的复原效果分别如图4(d)、(e)、(f)所示。

图4　利用吸引子点阵重构图像

在图像复原的时候，如果绘制出一个点，将这个点的周围点也绘制出来，可以加速图像复原。例如，当每次绘制周围的3×3个点时，使用前100个(p,q)就可以绘制出如图5(a)所示效果，与图4(c)相比，复原效果更好。如果绘制每点周围5×5个点，那么使用前49个(p,q)就可以复原出如图5(b)所示效果。

图5　利用吸引子点阵重构图像(每次绘制每点周围多个点)

49个近似吸引子叠加在一起，能够重构图像轮廓；这意味着49个稀疏的三维数组代表着一个Lena图像；需要的时候组合，不需要的时候可以分散放到吸引子库中。

4　结论

在已有文献的基础上，将辅助函数改为离散余弦变换基函数，与图像构造动力系统，得到的近似吸引子可以作为视频图像分割的依据。这种方法与其他图像特征提取方法存在着本质上的不同。

视频图像数据是一种大数据，既然这种方法可以应用于图像处理、图像模式提取，那么也可以经过改进后，用于其他数据处理。

进一步的工作是，改进这种数据存储与表达方式，尝试建立一种新的索引方式，即点阵与概念索引方式。例如“脸”这个概念，是否对应着“高一级”的点阵，即吸引子点阵的一种索引结构。

这是一种特征提取与存储方法，是否可以成为一种数据分解与重构的方法还有待于进一步研究。

参考文献

[1] KOMMINENI J, SATRIA M, MOHD S S. Content based image retrieval using colour strings comparison[J]. Procedia Computer Science, 2015，50：374-379.

[2] Wu Fei, Wang Zhuhao, Zhang Zhongfei, et al. Weakly semi-supervised deep learning for multi-label image annotation[J]. IEEE Transactions on Big Data, 2015(1)：109-122.

[3] TEMESGUEN M, RUSSEL C H, TIMOTHY R T. Segmentation of pulmonary nodules in computed tomography using a regression neural network approach and its application to the lung image database consortium and image database resource initiative dataset[J]. Medical Image Analysis, 2015, 22(1)：48-62.

[4] Tian Xinmei, Lu Yijuan, STENDER N, et al. Exploration of image search results quality assessment[J]. IEEE Transactions on Big Data, 2015,1(3)：95-108.

[5] ZANG M, WEN D, WANG K, et al. A novel topic feature for image scene classification[J]. Neurocomputing, 2015, 148(1)：467-476.

[6] WEINMANN M, URBAN S, HINZ S, et al. Distinctive 2D and 3D features for automated large-scale scene analysis in urban areas[J]. Computers & Graphics, 2015, 49(7)：47-57.

[7] Yuan Yuan, Wan Jia, Wang Qi. Congested scene classification via efficient unsupervised feature learning and density estimation[J]. Pattern Recognition, 2016, 56：159-169.[8] Lin Liang, Wang Xiaolong, Yang Wei, et al. Discriminatively trained and-or graph models for object shape detection[J] IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(5)：959-972.

[9] 于万波, 赵斌. 曲面迭代混沌特性研究[J] 物理学报, 2014，63(12)：29-39.

[10] 于万波. 截面的几何形状决定三维函数的混沌特性[J]. 物理学报, 2014(12)：20-28.

[11] 于万波, 王大庆. 图像函数与三角函数迭代的混沌特性研究[C]. 第17届全国图象图形学学术会议论文集，北京: 北京交通大学出版社, 2014.

[12] 于万波, 王大庆. 曲面迭代混沌特性及其在人脸识别中的应用[J]. 计算机辅助设计与图形学学报, 2015，27(12)：2264-2271.

[13] 于万波. 混沌的计算分析与探索[M]. 北京：清华大学出版社，2016.

Expression of chaotic pattern of image data based on iteration

Yu Shuo1，Li Sisi1，Yu Wanbo2

(1. School of Business Administration, Dalian University of Finance and Economics, Dalian 116600,China; 2. College of Information, Dalian University, Dalian 116622, China)

This paper used the discrete cosine transform (DCT) basis function as an auxiliary function together with the gray image of the sequence to construct the dynamic system, and then achieved the trajectory point set (approximate attractor) by iteration. This attractor can be used to distinguish the different scenes of the video image. It Used a number of DCT basis function to construct respectively with an image dynamic system to generate a number of approximate attractor. These attractors can be used as image features for image recognition, and can also be used to reconstruct the original image.

image data; chaotic attractor; discrete cosine transform basis function

辽宁省自然科学基金(201602034)

TP391

ADOI： 10.19358/j.issn.1674- 7720.2016.18.011

2016-05-25)

于硕(1990-)，女，硕士，助教，主要研究方向：大数据、图像处理。

李思思(1994-)，女，本科生，主要研究方向：图像处理。

于万波(1966-)，通信作者，男，博士，副教授，主要研究方向：图形图像、人工智能。E-mail：yu_wb@126.com。