胶结充填体力学特性的加载速率效应试验

李雅阁，金龙哲，谭　昊，王　浩

(1. 北京科技大学 土木与环境工程学院， 北京 100083； 2. 北京科技大学 矿山避险技术研究中心， 北京 100083)



胶结充填体力学特性的加载速率效应试验

李雅阁1，2，金龙哲1，2，谭昊1，王浩1

(1. 北京科技大学 土木与环境工程学院， 北京 100083； 2. 北京科技大学 矿山避险技术研究中心， 北京 100083)

为探究胶结充填体在不同加载速率状态下的力学参数变化规律及其破坏模式，采用数显式压力机分别对2.0、4.0、6.0、8.0 mm/min这4种加载速率下的胶结充填体开展单轴压缩试验. 试验结果表明：在2.0～8.0 mm/min加载速率范围内，加载速率对于胶结充填体的抗压强度值和割线模量均具有明显的强化效应，且峰值抗压强度值和割线模量随加载速率增大而增大. 峰值抗压强度与加载速率呈多项式函数规律，而割线模量与加载速率则呈指数函数分布规律. 且随着加载速率增大，胶结充填体试件破坏形式表现为拉剪混合破坏向单一剪切破坏形式逐渐转化. 研究结果揭示了胶结充填体的力学特性加载速率效应，为研究充填体破坏机制提供一定的参考依据.

胶结充填体；单轴抗压强度；加载速率；割线模量；破坏模式

地下开采是我国矿山开采的主要手段之一，实现采空区充填不但能够保护地表塌陷，而且能够减少地表尾矿的堆存，对于环境保护具有重要意义. 充填料浆经地表一旦进入地下采空区后，其不仅受到地应力、温度和渗流压等多物理场综合作用，同时受到爆破扰动作用影响. 国内外学者对不同受力状态下的充填体开展了较多的研究工作，常用的研究手段有基础实验法、数值模拟法和理论预测法等[1-4]，而国内外针对尾砂胶结充填体在不同加载速率条件下的强度变化研究则相对较少. 加载速率作为动态力学研究的基本参量之一，其变化范围往往较大. 国内外对于岩石或煤岩体在不同加载速率下的力学特性进行了较完善的研究工作[5-7],一般认为应变速率10-4s-1属于低应变速率；大于10-2s-1属于高应变速率，即动态加载[8]. 尹乾等[9]和许金余等[10]以高温后的花岗岩和大理岩为研究对象，开展了不同加载速率下的巴西劈裂试验，分析了温度和加载速率对花岗岩的断裂特性；徐小丽等[11]从能量角度研究了不同加载速率下花岗岩的破坏机制，认为加载速率对于岩石的力学性质及破坏方式具有重要的影响；李海涛等[12]对煤进行了不同加载速率单轴压缩力学试验，发现其强度随加载速率增加表现出先升高后降低的现象，将转折点对应的加载速率定义为临界加载速率；金浏等[13]探讨了加载速率及其突变对混凝土压缩破坏模型及宏观力学性能，并结合数值模拟手段分析了细观组分应变率效应的影响，国内学者对不同岩石试件也进行了相关研究[14-15]. 本文利用某矿山尾矿为原料，制作灰砂比为1/6，质量浓度为75%的胶结充填体试件，进行不同加载速率下的单轴压缩试验来研究其力学参数变化规律及其破坏模式.

1　试件制备与加载设备

1.1试验材料和设备

试验原料采用某矿山尾矿，42.5R硅酸盐水泥作为胶骨料. 尾矿样品经烘干处理后，采用LS-909激光粒度分析仪对其粒径分布特性进行研究. 图1所示为该矿山尾矿的粒径分布曲线.

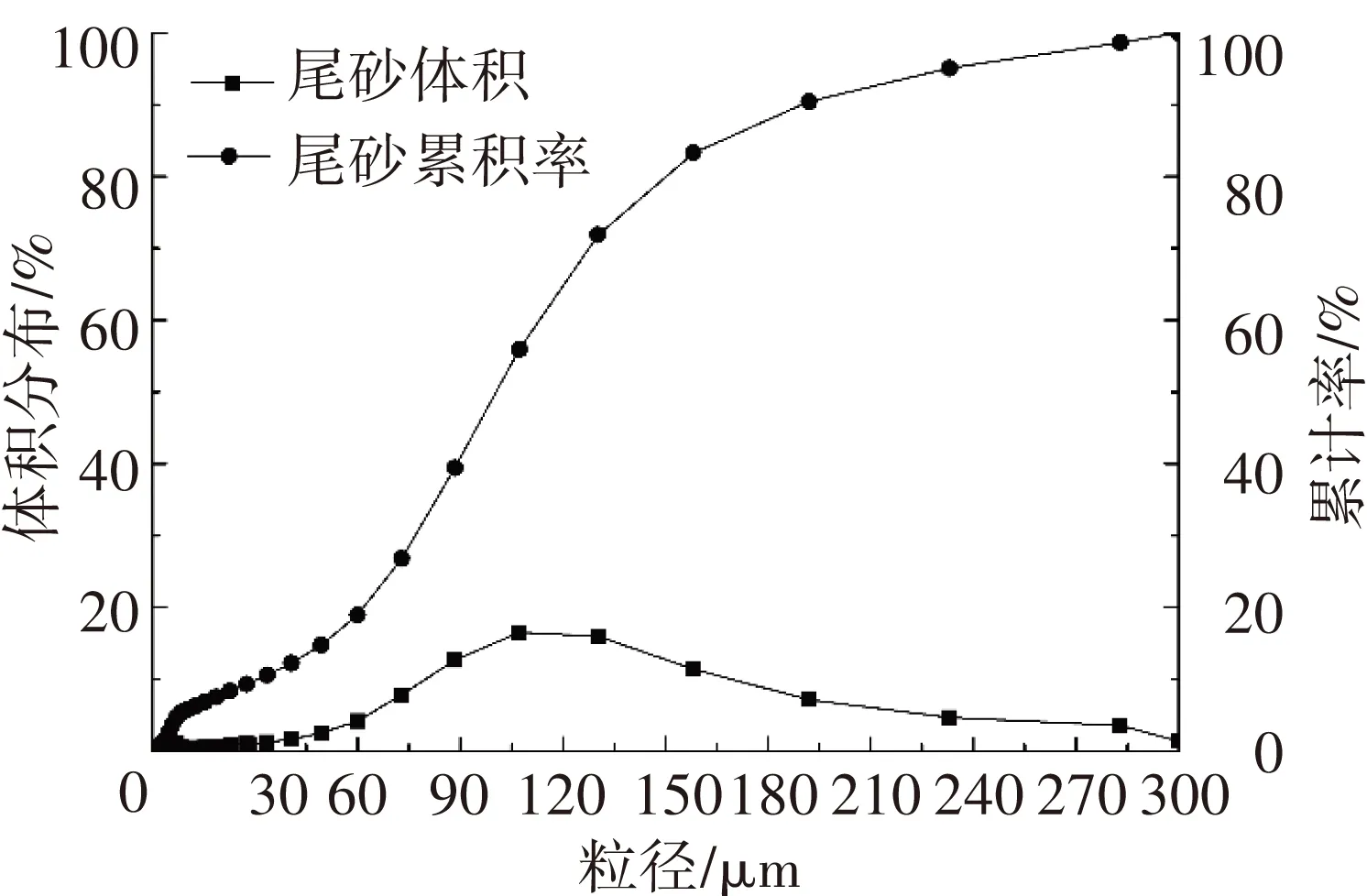
图1　分级尾砂粒径分布

通过试验数据分析得到尾砂粒径累积分布结果为d10=30.74 μm，d50=100.54 μm，d90=190.04 μm，dav=107.43 μm. 其中分级尾砂大于100.54 μm的颗粒约占50%，说明该分级尾砂属于粗粒级尾砂.

应力加载试验采用SANS数显式固定位移压力机，该试验机通过对试件施加固定位移进行加载，并能够实时记录轴向载荷与轴向变形曲线，并通过导出excel文件输出试验数据.

1.2试验方案与假设

设计采用灰砂比为1/6，质量浓度为75%的充填体料浆制作试件，养护龄期为60 d. 养护温度为(20±5)℃，相对湿度为95%±5%. 利用砂纸对充填体试件的两端进行小心打磨，使得试件上下面平整度控制在0.02 mm以内，得到充填体试件如图2所示. 本试验将加载速率作为主要研究对象，按照2.0、4.0、6.0、8.0 mm/min 4种加载速率开展分级尾砂胶结充填体试件的单轴压缩试验，得到其应力-应变全过程曲线. 并分析不同加载速率下，充填体试件破裂形态及裂纹发展规律.

图2　尾砂胶结充填体试件

2　试验结果分析

2.1加载速率与峰值抗压强度定量关系分析

根据设计方案，本试验的胶结充填体试件共计36个，按照加载速率由低到高的顺序开展单轴压缩试验. 不同加载速率下的胶结充填体峰值强度结果见表1. 加载速率为2.0、4.0、6.0、8.0 mm/min时，对应峰值抗压强度分别为2.98、3.01、3.06、3.12 MPa.

表1不同加载速率下的充填体强度值

Tab.1Cemented filling body strength value under different loading rates

试件编号加载速率/(mm·min-1)峰值强度/MPa2-12.02.562-22.03.212-32.02.662-42.03.022-52.03.262-62.03.174-14.03.284-24.03.004-34.02.834-44.0—4-54.03.034-64.02.916-16.02.776-26.03.266-36.02.706-46.0—6-56.0—6-66.03.498-18.0—8-28.02.548-38.02.358-48.03.258-58.03.558-68.03.91

需要说明的是，试件6-4由于加载初始设置量程较小，当轴向应力超过6 kN后，加载设备自动停止. 因此，数据异常需要剔除；试件8-1与其余5组试验结果相差较大，故作剔除处理.

根据表1统计结果，在2.0～8.0 mm/min加载速率时，随着加载速率增大，胶结充填体试件的峰值抗压强度增加. 说明加载速率对于充填体试件的峰值抗压强度具有明显的强化效应. 同时当加载速率从2.0 mm/min增到4.0 mm/min时，平均峰值抗压强度从2.98 MPa增长到3.01 MPa. 而当加载速率达到6.0 mm/min时，对应强度为3.06 MPa. 而从6.0 mm/min增大到8.0 mm/min后，平均峰值强度从3.06 MPa增大到3.12 MPa，增幅仅为3.8%. 采用线性、指数、对数和多项式4种方式对峰值抗压强度与加载速率进行拟合，计算结果如图3所示，其中σp为峰值抗压强度值，MPa；v为加载速率，mm/min.

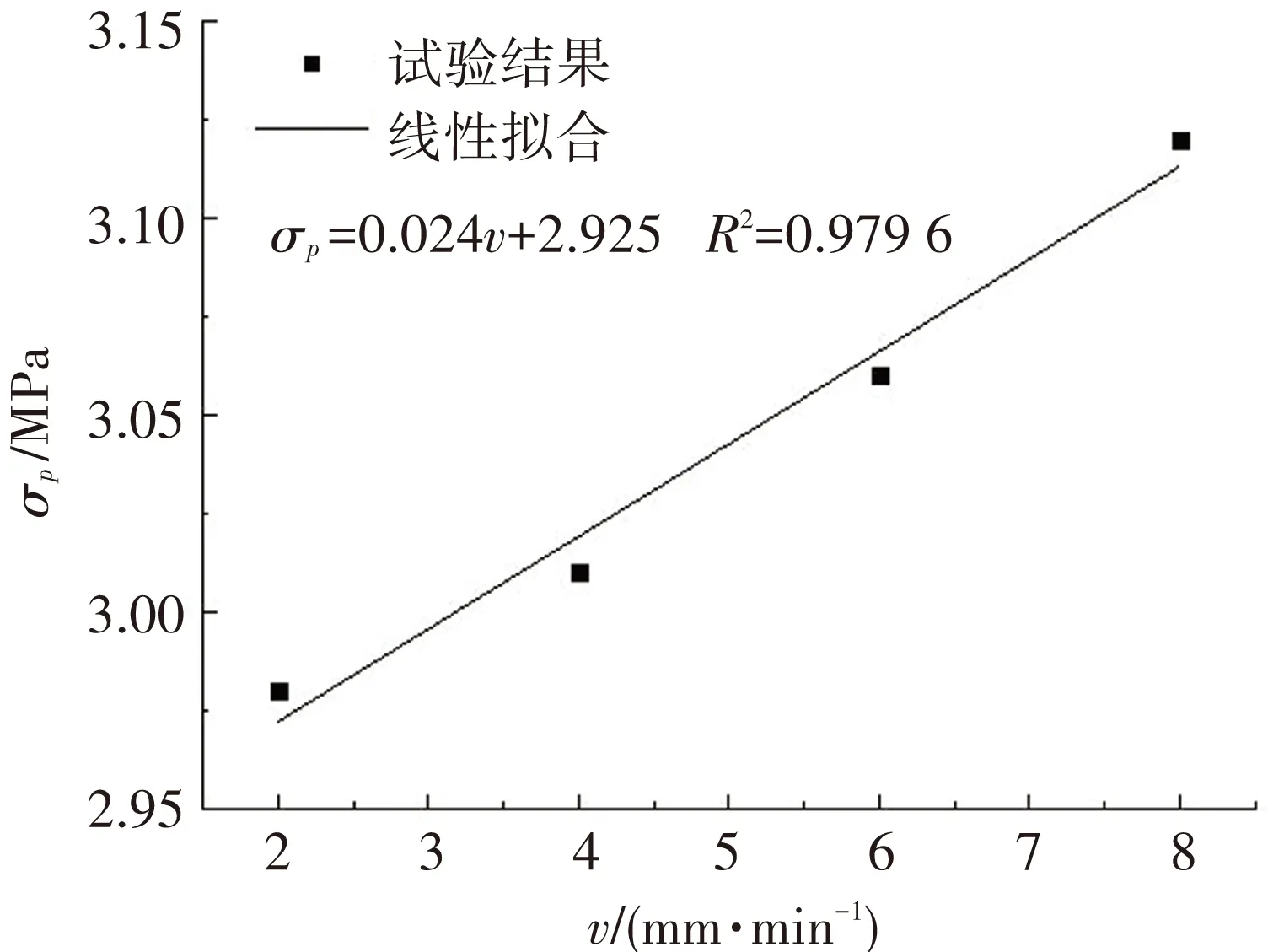
(a) 线性拟合

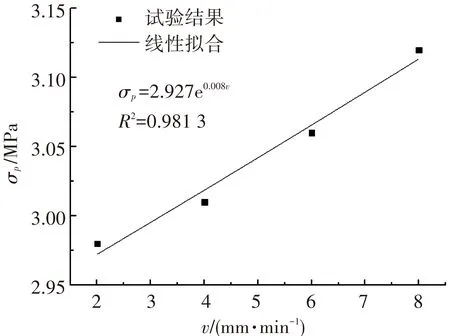
(c) 指数拟合

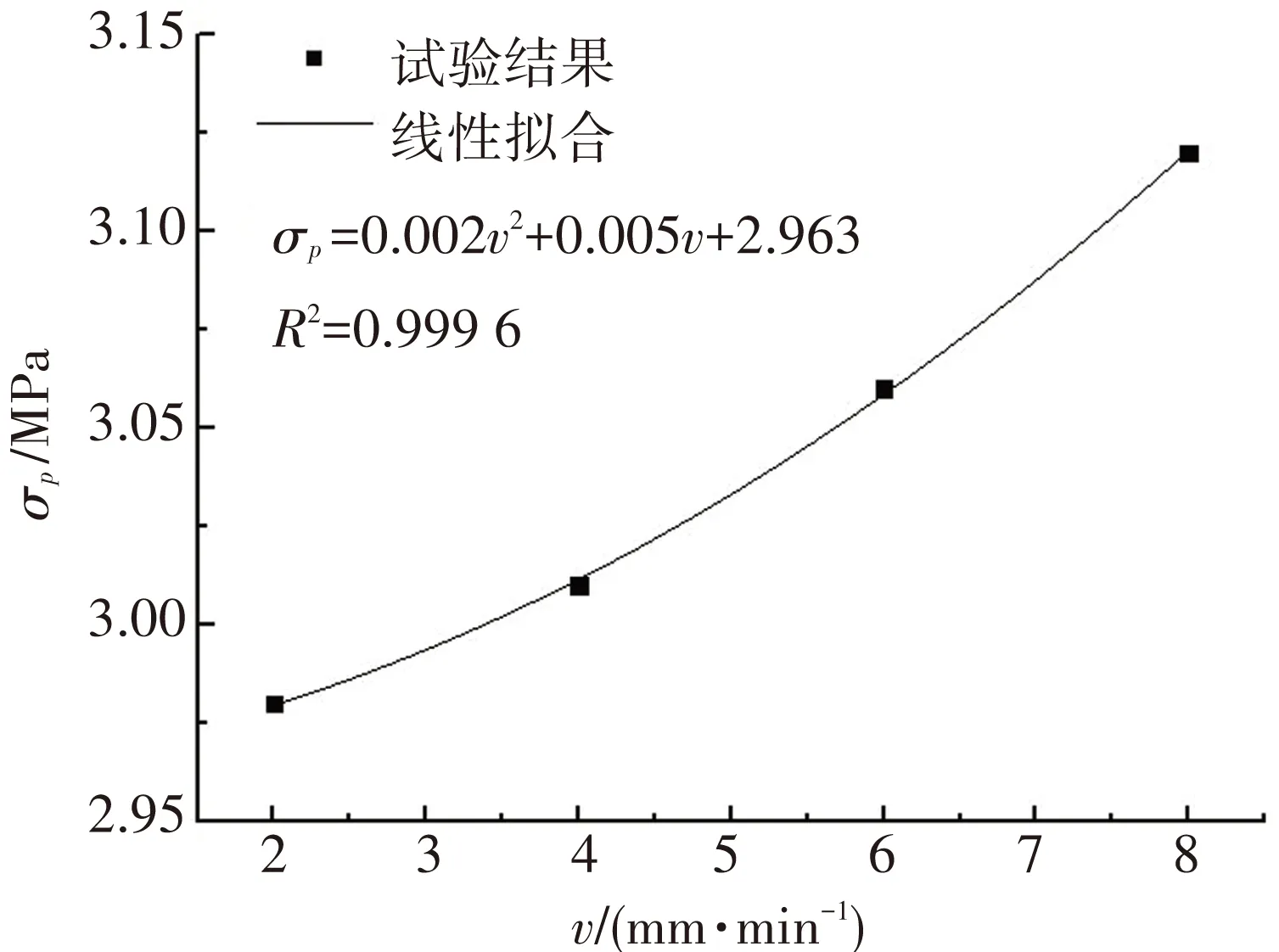
(b) 多项式拟合

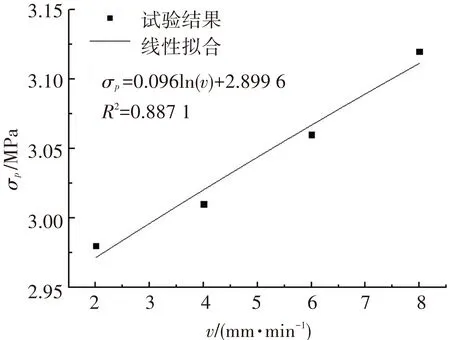
(d) 对数拟合

分析图3拟合结果，线性、指数和对数拟合复相关系数最大为98.13%，最小为88.71%，拟合程度均较高. 而多项式拟合方式的复相关系数最高，达到99.96%. 说明σp=0.002v2+0.005v+2.963的多项式拟合方式能够更好地反映充填体峰值抗压强度与加载速率之间定量关系.

2.2加载速率与割线模量定量表征

借鉴岩石力学中反映岩石平均刚度的割线模量对不同加载速率下的胶结充填体长期强度进行研究. 这里选取50%的峰值抗压强度点与坐标原点连线的斜率作为割线模量值，即

(1)

式中:Es50为割线模量，GPa； σp50为单轴抗压强度的50%应力值，MPa；εp50为试件对应的轴向应变值.

结合胶结充填体的应力-应变关系曲线进行割线模量值求解，最终得到的计算结果见表2所示. 加载速率为2.0、4.0、6.0、8.0 mm/min时，割线模量平均值分别为1.239、1.509、1.931、2.323 GPa.

为探究胶结充填体割线模量与加载速率的定量关系，对表2计算结果进行线性、指数和对数拟合，将计算结果的复相关系数R2作为评判依据. 图4为3种拟合方式的拟合曲线.

分析图4中3种不同的拟合方式发现，线性、指数和对数拟合的复相关系数分别为0.988 1、0.991 9、0.944 4，均表现出较高的拟合特性. 但指数拟合程度最高，说明指数拟合能够更好地表征加载速率与胶结充填体割线模量的定量关系. 同时发现，随着加载速率增大，割线模量随之增大. 说明加载速率对于胶结充填体的平均刚度也具有强化效应.

表2胶结充填体割线模量计算结果

Tab.2The calculation of secant modulus value of cemented filling body

试件编号加载速率/(mm·min-1)割线模量/GPa2-12.00.9452-22.01.0832-32.01.4342-42.01.0452-52.0—2-62.01.6864-14.01.7394-24.00.9374-34.01.0614-44.0—4-54.02.1614-64.01.6456-16.01.5376-26.01.6486-36.02.1756-46.0—6-56.0—6-66.02.3628-18.0—8-28.02.2288-38.0—8-48.02.2748-58.02.0538-68.02.736

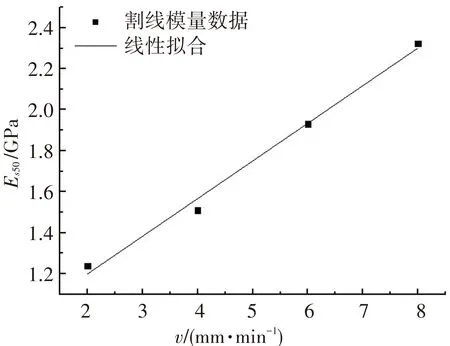
(a)线性拟合

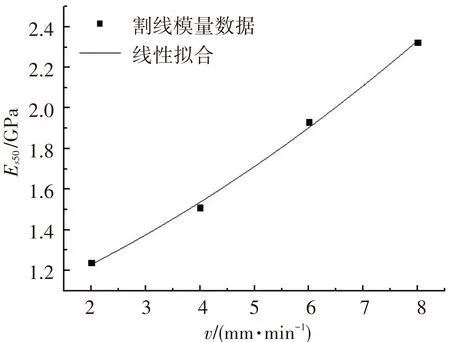
(b) 指数拟合

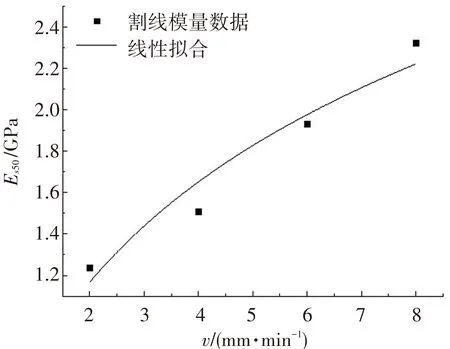
(c) 对数拟合

3　胶结充填体破坏模式分析

4种加载速率下的充填体破坏试件和破坏形式素描图见图5所示.

图5　不同加载速率下充填体试件破坏素描

Fig.5Photograph and failure sketch of specimens in different loading rates

4　结　论

1)加载速率对于胶结充填体的抗压强度值和割线模量值均具有明显的强化效应，且充填体峰值抗压强度随着加载速率的增大而增大；随着加载速率增大，割线模量随之增大. 峰值抗压强度与加载速率呈多项式函数规律，而割线模量与加载速率则呈指数函数分布规律.

2)分析充填体试件的破坏形式发现，随着加载速率增大，试件破坏形式逐渐表现为拉剪混合破坏向单一剪切破坏形式的转化. 且加载速率越快，充填体在达到破坏所作用的时间越短.

3)该试验得到的结果仅对灰砂比1/6，质量浓度为75%的胶结充填体进行试验得到的，是否适用于其他充填材料，需要开展进一步的研究工作.

[1] GHIRIAN A, FALLM. Coupled thermos-hydro-mechanical-chemical behaviour of cemented paste backfill in column experiments part I: physical, hydraulic and thermal processes and characteristics[J]. Engineering Geology, 2013, 164: 195-207.

[2] NASIR O, FALL M. Coupling binder hydration, temperature and compressive strength development of underground cemented paste backfill at early ages[J]. Tunnelling and Underground Space Technology, 2010, 25: 9-20.

[3] NISTICO N, PALLINI F, ROUSAKIS T, et al. Peak strength and ultimate strain prediction for FRP confined square and circular concrete sections[J]. Composites: Part B, 2014, 67: 543-554.

[4] 魏微，高谦．改进的BP神经网络模型预测充填体强度[J]．哈尔滨工业大学学报，2013，45(6)：90-95.

WEI Wei, GAO Qian. Strength prediction of backfilling body based on modified BP neural network[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 90-95.

[5] 曹安业，井广成，窦林名，等. 不同加载速率下岩样损伤演化的声发射特征研究[J]. 采矿与安全工程学报，2015, 32(6): 923-928.

CAO Anye, JING Guangcheng, DOU Linming, et al. Damage evolution law based on acoustic emission of sandy mudstone under different uniaxial loading rate[J]. Journal of Mining & Safety Engineering, 2015, 32(6): 923-928.

[6] 李战鲁，王启智. 加载速率对岩石动态断裂韧度影响的实验研究[J]. 岩土工程学报，2006, 28(12): 2116-2120.

LI Zhanlu, WANG Qizhi. Experimental research on effect of loading rate for dynamic fracture toughness of rock[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2116-2120.

[7] ROSA L, YU R C, RUIZ G, et al. A loading rate dependent cohesive model for concrete fracture[J]. Engineering Fracture Mechanics, 2012, 82(3): 195-208.

[8] 尹小涛，葛修润，李春光，等. 加载速率对岩石材料力学行为的影响[J]. 岩石力学与工程学报，2010, 29(增刊1): 2610-2615.

YIN Xiaotao, GE Xiurun, LI Chunguang, et al. Influences of loading rates on mechanical behaviors of rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Sup1): 2610-2615.

[9] 尹乾，靖洪文，苏海健，等. 高温后花岗岩断裂特性的加载速率效应研究[J]. 中国矿业大学学报，2015, 44(4): 597-603.

YIN Qian, JING Hongwen, SU Haijian, et al. Loading rate effect on fracture properties of granite after high temperature[J]. Journal of China University of Mining & Technology, 2015, 44(4): 597-603.

[10]许金余，刘石. 加载速率对高温后大理岩动态力学性能的影响研究[J]. 岩土工程学报，2013, 35(5): 879-883.

XU Jinyu, LIU Shi. Effect of impact velocity on dynamic mechanical behaviors of marble after high temperatures[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(5): 879-883.

[11]徐小丽，陈琳，高峰，等. 花岗岩的加载效率效应及能量机制研究[J]. 固体力学学报，2015, 36(2): 154-163.

XU Xiaoli, CHEN Lin, GAO Feng, et al. Studies on loading rate effects and energy mechanism of granite[J]. Chinese Journal of Solid mechanics, 2015, 36(2): 154-163.

[12]李海涛，蒋春祥，姜耀东，等. 加载速率对煤岩力学行为影响的试验研究[J]. 中国矿业大学学报，2015, 44(3): 430-436.

LI Haitao, JIANG Chunxiang, JIANG Yaodong, et al. Mechanical behavior and mechanism analysis of coal samples based on loading rate effect[J]. Journal of China University of Mining & Technology, 2015, 44(3): 430-436.

[13]金浏，杜修力. 加载速率及其突变对混凝土压缩破坏影响的数值研究[J]. 振动与冲击，2014, 33(19): 187-193.

JIN Liu, DUXiuli. Effects of loading rate and its sudden change on concrete compressive failure[J]. Journal of Vibration and Shock, 2014, 33(19): 187-193.

[14]周辉，杨艳霜，肖海斌，等. 硬脆性大理岩单轴抗拉强度特性的加载速率效应研究—试验特征与机制[J]. 岩石力学与工程学报，2013, 32(9): 1868-1875.

ZHOU Hui, YANG Yanshuang, XIAO Haibing, et al. Research on loading rate effect of tensile strength property of hard brittle marble—test characteristics and mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1868-1875.

[15]纪文栋，杨春和，姚院峰，等. 应变加载速率对盐岩力学性能的影响[J]. 岩石力学与工程学报，2011, 30(12): 2507-2513.

JI Wendong, YANG Chunhe, YAO Yuanfeng, et al. Effects of loading strain rate on mechanical performances of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2507-2513.

(编辑魏希柱)

Experiment of loading rate effect on mechanical characteristics of cemented filling body

LI Yage1,2, JIN Longzhe1,2，TAN Hao1, WANG Hao1

(1.School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China;2.Mine Emergency Technology Research Center, University of Science and Technology Beijing, Beijing 100083, China)

In order to investigate the mechanical parameters and failure modes of cemented filling body under different loading rates, four loading rates between 2.0 mm/min and 8.0 mm/min were utilized to develop uniaxial compressive test. The research shows that: the loading rate has an obvious strengthening effect on the peak strength and secant modulus value of the cemented filling body samples. As the loading rate increases, the peak strength and secant modulus also rise. In addition, the peak strength corresponds to the loading rates, fitting a polynomial function. And the secant modulus and loading rate meet the exponential function. Along with the increasing loading rates, the cemented filling body samples show a gradual transformation from mixed failure to the single shear failure mode. The test characteristics of the loading rate effect on the mechanical properties of cemented filling body are revealed, which provides a theoretical basis for the study of failure mechanism of filling body.

cemented filling body; uniaxial compressive strength (UCS); loading rate; secant modulus； failure modes

10.11918/j.issn.0367-6234.2016.09.009

2015-12-14

国家自然科学基金(51574017)

李雅阁(1983—)，男，高级工程师，博士研究生；

金龙哲(1962—)，男，教授，博士生导师

金龙哲， lzjin@ustb.edu.cn

TD853

A

0367-6234(2016)09-0049-05