残差修正模型在森林火灾预测中的应用

连素兰, 何东进, 纪志荣, 洪　伟, 游巍斌, 曹　彦, 胡　新

(1.福建农林大学计算机与信息学院；2.福建农林大学林学院；3.福建农林大学科教基地管理中心，福建 福州 350002)



残差修正模型在森林火灾预测中的应用

连素兰1, 何东进2, 纪志荣1, 洪伟2, 游巍斌2, 曹彦1, 胡新3

(1.福建农林大学计算机与信息学院；2.福建农林大学林学院；3.福建农林大学科教基地管理中心，福建 福州 350002)

基于1990-2013年福建省森林火灾发生次数建立残差修正模型，并与BP神经网络模型、马尔科夫链模型、赋权组合预测模型进行比较.结果表明：残差修正预测模型的预测精度达到95.33%，而BP神经网络模型预测精度是87.77%，马尔科夫链模型预测精度为74.85%，赋权组合预测模型预测精度为88.3%，残差修正模型预测效果优于其他3个模型，说明使用其对离散的森林火灾数据进行短期预测是有效可行的.

森林火灾; 残差修正模型; 反向传播神经网络; 马尔科夫链; 赋权组合模型; 福建省

森林资源是人类生活生产所必须需的一种重要资源，可持续发展的森林资源对国民经济发展起着非常重要的作用.然而，森林火灾不仅摧毁森林资源、破坏自然环境、造成环境污染，而且给相关国家和人民造成了巨大的经济损失.全球每年发生森林火灾在2.20×105次以上，每年烧毁林地面积超过6.40×106hm2，森林火灾的危害非常之大[1].国外森林火灾研究主要集中在技术层面和理论层面，包括森林火灾预测预报[2]、森林火灾影响因素研究[3]、森林火灾损失评估[4].国内关于森林火灾预测研究渐渐由定性分析转向定量分析发展，由普通数理统计向具有显著物理意义的数学模型发展，其预测方法包括灰色预测模型[5]、分形理论[6]、马尔科夫链法[7]、人工神经网络模型[8]、突变级数法[9]等等.

第八次全国森林资源清查结果显示，全国森林面积2.08×109hm2，森林覆盖率21.63%[10].福建省是全国森林火灾的高发区，全省85个县(市、区)中被列为国家重点森林火险单位的有64个，占全省县级行政区划单位的77%[11].森林火灾发生次数是森林火灾强度的一个重要体现，通过预测森林火灾发生次数能够侧面反映一个区域的火灾程度.本文基于1990-2013年福建省森林火灾数据，引入一种新的预测方法，构建残差修正模型[12]，为森林火灾的预测提供新的研究方法，并与目前常用的反向传播神经网络模型、马尔科夫链模型和赋权组合预测模型进行预测效果比较.

1　研究区概况与数据来源

福建省东北与浙江省毗邻，西、西北与江西省接界，西南与广东省相连，东隔台湾海峡与台湾岛相望，土地总面积1.24×107hm2，海域面积达1.36×107hm2，境内山地、丘陵面积最多，约占全省总面积的80%以上，土壤肥沃.福建省第8次森林资源清查结果显示，福建省森林面积8.01×106hm2，森林覆盖率65.95%，居全国第一，活立木总蓄积6.67×108m3，森林蓄积6.08×108m3，每公顷蓄积量100.20 m3，生态功能等级达到中等以上的面积占95%[13]，由此可见，福建省是我国南方的重点林业大省，其林业发展在我国林业中起着重大作用.本文研究收集的数据来源于《中国统计年鉴》、《中国林业统计年鉴》、《福建统计年鉴》以及中华人民共和国国家统计局网的森林火灾情况.

2　研究方法

2.1反向传播神经网络模型

反向网络(back propagation, BP)是目前应用最广泛的神经网络模型之一，由Rumelhart和McCelland为首的科学家小组于1986年提出，是一种多层前馈网络，该网络的主要特点是信号前向传递，误差逆传播.在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层.每一层的神经元状态只影响下一层神经元状态.如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出不断逼近期望输出.BP神经网络模型拓扑结构包括输入层、隐含层和输出层，每一层由若干个神经元组成[14]，如图1所示.

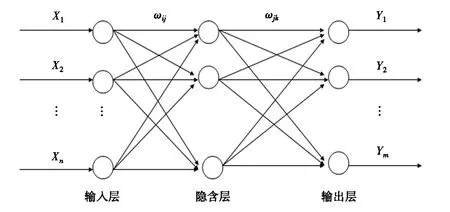
图1　BP神经网络拓扑结构图

图1中，X1,X2,…,Xn是BP神经网络的输入值，Y1,Y2,…,Ym是BP神经网络的预测值，ωij和ωjk为BP神经网络权值.从图1可以看出，BP神经网络可以看成一个非线性函数，网络输入值和预测值分别为该函数的自变量和因变量.当输入节点数为n、输出节点数为m时，BP神经网络就表达了从n个自变量到m个因变量的函数映射关系.

2.2马尔科夫链模型

马尔科夫链是一种具有离散状态集的随机过程，其预测模型是利用某一变量的当前状态去预测未来某一时刻这一变量所处的状态，预测模型[15]可表示为：

(1)

(2)

具体的预测步骤为：①划分状态，状态的划分依据数据特点而定，本文采用均值—标准差法[7]来划分预测对象的状态.②计算转移概率矩阵.③建立模型，确定预测状态.

2.3赋权组合预测模型

组合预测法是由Bates和Granger于1969年首次提出，其基本思想是：对于同一个预测问题进行多种角度预测，从而得到多种有一定差异的预测结果.由于这些结果各自所承载的信息价值不同，所以可以用一定的组合方式将其组合成一个综合的预测结果，以便将他们各自所承载的有价值的信息提取出来[16].

(3)

由于本文仅运用两种单一的预测模型，因此其组合权重为：

(4)

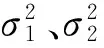
2.4残差修正模型

首先利用1990-2007年福建省森林火灾发生次数数据建立一种预测模型，并求出预测误差序列ω=(ω1,ω2,…ωn)，对预测误差序列值ω建立另一种模型，公式为：

xt-f1(t)=ωt=f2(t)+εtt=1,2,…,N

(5)

其中xt为t期的实际观测值，f1(t)为第一种模型观测值，f2(t)为第二种模型观测值，εt为第二种预测模型模拟ωt的残差序列，也成为白噪声序列，因此预测公式如下：

(6)

2.5预测精度的测定

预测精度一般指预测模型拟合的好坏程度，即预测模型所产生的模拟值与历史实际值拟合程度的优劣[17].

(7)

Pc=(1-MAPE)×100%

(8)

3　结果与分析

本文用福建省1990-2007年这18年的森林火灾发生次数作为时序数据建立预测模型，比较BP神经网络模型、马尔科夫链模型、赋权组合模型和残差修正模型的预测效果.

表1　状态划分区间Table 1　Interval division of state of forest fire

从1990-2007年福建省森林火灾发生次数的预测结果(表2)可以看出，残差修正模型的预测值的预测精度最高，为91.2%，平均相对误差绝对值(MAPE)最低，为0.088，而马尔科夫链预测模型的预测精度最低，只有64.3%，平均相对误差绝对值为0.357，BP神经网络模型的预测精度为89.87%，平均相对误差绝对值为0.101 3，赋权组合模型的预测精度为90.01%，平均相对误差绝对值为0.099 9，其预测精度高于BP神经网络模型和马尔科夫链模型，但比残差修正模型低.

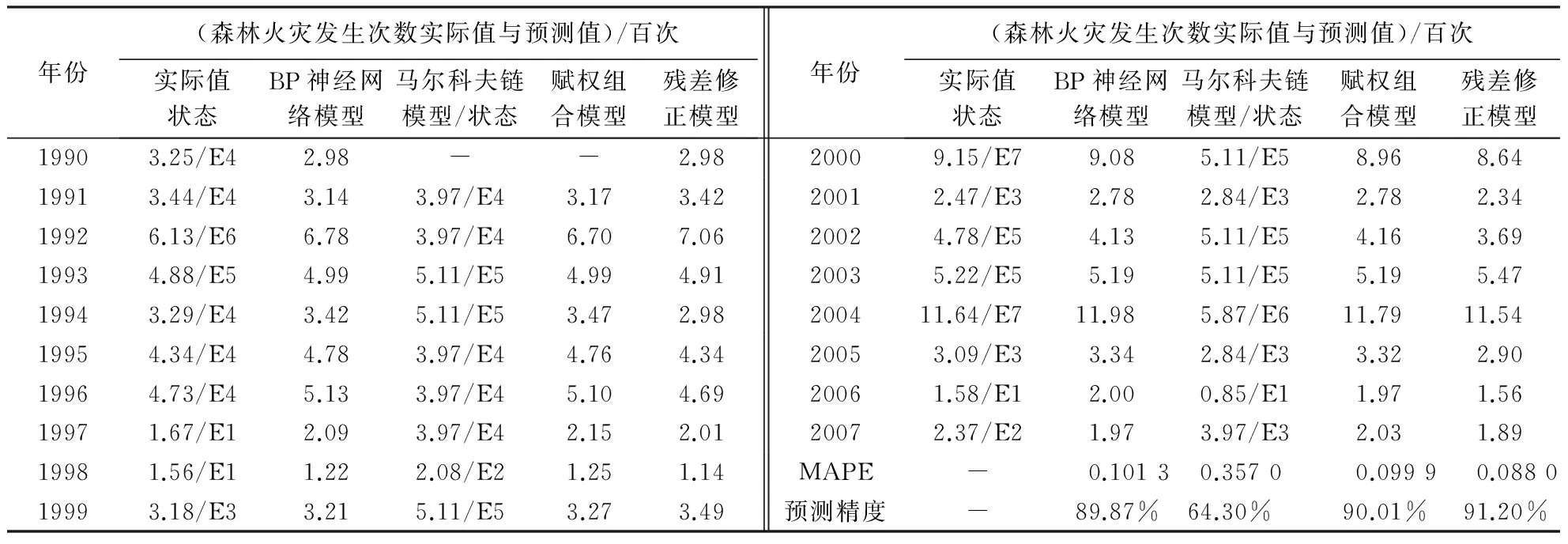
表2　1990-2007年福建省森林火灾发生次数的预测结果Table 2　Prediction on forest fire in Fujian Province from 1990 to 2007

为了进一步验证残差修正模型的预测效果是最优的，本文进一步预测2008-2013的森林火灾发生次数，并进行预测精度比较.

从2008-2013年福建省森林火灾发生次数的预测结果(表3)可以看出，BP神经网络模型的预测精度为87.77%，对2012年的预测效果比较差，相对误差为47.79%，这是因为BP神经网络具有很强的样本依赖性，本研究训练数据是1990年至2007年，而2012年的森林火灾发生次数是1990-2013年中整个时间序列的极值点，使得整个网络模型的预测能力受到了影响.马尔科夫链模型的预测精度只有74.85%，对2010年和2013年的预测相对误差都超过50%，主要是由于马尔科夫链模型是对状态的预测，状态预测的偏离程度以及状态上下限的设置都会影响模型的预测效果.BP神经网络模型的预测效果比马尔科夫链模型的预测效果要好，但两种模型的预测能力均不是很高，其原因主要是有以下两点：其一模型数据是离散的整值数据，相对于连续数据来说，会造成很大的预测误差，其二是建立的模型是单一模型，BP神经网络模型隐含层神经元个数和马尔科夫链状态区间的选取都较为主观，这使得从两种单一模型中提取数据的信息不够充分有效.赋权组合模型减小了预测误差，预测精度达到88.30%，比BP神经网络模型和马尔科夫链模型这两个单一模型的预测效果好，但是对于2012年的预测结果出现异常，主要是由于赋予了BP神经网络模型较大的权重，而BP神经网络模型在2012年的预测误差很大，因此影响了赋权组合预测模型的预测效果.残差修正模型的预测值波动范围比较小，相对误差范围在10%以内，其最大相对误差为9.94%，最小相对误差为0.11%，精度提高到95.33%，比单一模型和赋权组合预测模型的预测效果都要好，因此运用残差修正模型对福建省森林火灾发生次数进行预测大大提高了模型的预测效果.

4　结论与讨论

目前BP神经网络模型和马尔科夫链模型各有优缺点，在实践中发现，BP神经网络具有较强的非线性映射能力，对于离散的整值数据，模型的预测效果有时好，有时预测误差很大，甚至完全失效.马尔科夫链模型所需数据少，不需要从复杂的预测因子中寻找各因素之间的相互规律[18]，但是由于转移概率矩阵在长期预测中会发生变化，因此不适合做长期预测.组合预测模型很好的结合了二者的优缺点，提高了预测精度.本文基于1990-2013年福建省森林火灾数据建立残差修正预测模型，并与BP神经网络模型、马尔科夫链模型和赋权组合预测模型进行预测效果比较，结果发现残差修正模型的预测效果优于BP神经网络模型、马尔科夫链模型和赋权组合预测模型的预测效果，预测精度显著高于其它三个模型，因此在预测森林火灾发生次数的应用中能取得很好的预测效果，使用其对离散的整值数据进行预测是有效且可行的.

表3　2008-2013年福建省森林火灾发生次数的预测结果Table 3　Predictions on the number of forest fire in Fujian Province from 2008 to 2013

本文所构建的残差修正模型虽然比较准确的反映福建省森林火灾发生次数，取得了短期的理想预测值，但是由于预测模型是依据森林火灾的历史资料建立的，模型精度取决于建模期间系统的稳定状态，因此随着预测次数的增加，预测结果仍存在一定的局限性和不确定性，需要不断修正和优化模型，从而为福建省森林火灾预测及防治提出更加合理合适的建议和策略.

[1] 舒立福,田晓瑞.国外林火现状与展望[J].世界林业研究,1997,10(2):28-36.

[2] BROWN T J, HALL B L, WESTERLING A L. The impact of twenty-first century climate change oil wildland fire danger in the western United States: An applications perspective[J]. Climatic Change, 2004,62(1):365-388.

[3] 张海军.河南省火灾影响因素的空间分析[J].地理科学进展,2014,33(7):958-968.

[4] BRENNER J, COEN J, MCLELLAN S.Assessing fire risk in florida using integrated gIS and remote sensing applications-50[J/OL].[2015-3-15]http://gis.Esri.com/library/userconf/proc01/professional/papers/pap826/p826.htm.

[5] 朱学平.森林火灾计量经济学研究[D].福州:福建农林大学,2012.

[6] 纪志荣,何东进,巫丽芸,等.基于时间序列的福建省森林火灾分形特征[J]. 福建农林大学学报(自然科学版),2013,42(5):508-511.

[7] 曹彦,何东进,洪伟,等.加权马尔科夫链在福建省森林火灾预测中的应用研究[J].西南林业大学学报,2014,34(3):62-66.

[8] 黄家荣,刘倩,高光芹,等.森林火灾成灾面积的人工神经网络BP模型预测[J].河南农业大学学报,2007,41(3):273-275.

[9] 朱学平,何东进,丁福立,等.基于突变级数法的福建省森林火灾评价分析[J].福建林学院学报,2011,31(4):295-299.

[10] 中国林业网.第八次全国森林资源清查主要结果[EB/OL].(2014-2-25)[2015-3-15]http://www.forestry.gov.cn/main/65/content-659670.html.

[11] 谭论.有效发挥森林防火在生态文明建设中的重要作用[J].森林防火,2013(3):24-28.

[12] 毛泽强,焦桂梅.一种改进的组合预测模型在猪瘟月新发生次数中的应用[J].中国科技论文在线精品论文,2013,6(1):23-31.

[13] 左研冰.福建省森林覆盖率升至65.95%保持全国第一[EB/OL].(2012-12-12)[2015-3-15]http://gb.cri.cn/42071/2013/12/12/6871s4354607.htm.

[14] 王小川,史峰,郁磊,等.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:01-10.

[15] 李海涛.运用马尔科夫预测法预测股票价格[J].统计与决策,2002(5):25-26.

[16] 谢素卿,曾珍香.组合预测结果的优化[J].河北工学院学报,1989(1):54-60.

[17] 徐国祥.统计预测与决策[M].上海:上海财经大学出版社,2012:191-193.

[18] 郝飞.马尔科夫预测法在股市预测中的应用[J].科学之友(学术版),2006(6):62-63.

(责任编辑:吴显达)

Residual correction model to predict the number of forest fire

LIAN Sulan1, HE Dongjin2, JI Zhirong1, HONG Wei2, YOU Weibin2, CAO Yan1, HU Xin3

(1.College of Computer & Information, Fujian Agriculture and Forestry University; 2.College of Forestry, Fujian Agriculture and Forestry University; 3.Science and Education Base Management Center, Fujian Agriculture and Forestry University, Fuzhou, Fujian, 350002, China)

To better predict occurrence of forest fire, residual correction model was established to predict the number of forest fire in Fujian Province from 1990 to 2013, comparing with data derived from back propagation (BP) neural network, Markov chain model, weighted hybrid model and compiled data. Results showed that residual correction model demonstrated the highest accuracy up to 95.33%, with accuracy of BP neural network model and weighted hybrid model being 87.77% and 88.3%, respectively, and Markov chain model being the least accurate model (74.85%). To summarize, residual correction mode was likely to be a feasible and effective model on discrete data prediction in short term, such as forest fire.

forest fire; residual correction model; back propagation neural network; Markov chain; weighted hybrid model; Fujian Province

2015-10-12

2015-11-15

国家自然科学基金项目(31370624、41301203).

连素兰(1990-)，女，硕士研究生.研究方向：自然资源调查与统计.Email：1337105020@qq.com.通讯作者何东进(1969-)，男，教授，博士生导师.研究方向：统计学与生态学.Email：fjhdj1009@126.com.

O213.9; S762.2

A

1671-5470(2016)05-0551-05

10.13323/j.cnki.j.fafu(nat.sci.).2016.05.012