流域地貌形态多尺度三维分形量化及尺度效应——以砒砂岩区二老虎沟为例

张传才, 秦 奋, 汪永新, 刘真真, 陈云生, 刘志丹

(1.河南大学 环境与规划学院, 河南 开封 475004; 2.安徽理工大学 测绘学院,安徽 淮南 232001； 3.河南大学 黄河中下游数字地理技术教育部重点实验室， 河南 开封 475004)



流域地貌形态多尺度三维分形量化及尺度效应
——以砒砂岩区二老虎沟为例

张传才1,2，3, 秦 奋1，3, 汪永新1, 刘真真1, 陈云生1, 刘志丹1

(1.河南大学 环境与规划学院, 河南 开封 475004; 2.安徽理工大学 测绘学院,安徽 淮南 232001； 3.河南大学 黄河中下游数字地理技术教育部重点实验室， 河南 开封 475004)

流域地貌形态的科学量化是地貌学研究和区域尺度土壤侵蚀模型研究中的热点问题之一。针对目前地貌形态分形量化模型中存在的地形模拟方法和模型结构不合理问题，基于GIS技术和分形理论改进了地貌形态分形量化模型，并使用无人机高分辨率DEM数据对砒砂岩区二老虎沟流域进行了多尺度地貌形态量化，进而研究了该区地貌形态三维分形量化的尺度效应。研究发现：(1) 随着尺度的降低，该区三维分形维数呈线性降低趋势，即地形复杂度呈线性降低趋势；(2) 砒砂岩区二老虎沟流域在10 m尺度地形复杂度已大大降低；(3) 根据多指标量化结果分析，地貌形态量化指标分为两类：地形复杂度指标和地形起伏度指标，前者具有明显的尺度效应，后者尺度效应不明显。

地形量化; 砒砂岩; 地貌三维分形; 尺度效应

尺度常常被定义为在研究对象或现象时采用的空间或时间单位，或者现象或过程在空间和时间上所涉及到的范围和发生的频率[1]。李霖[2]将尺度分为空间尺度、时间尺度和语义尺度，其中空间尺度又包括：地图比例尺、地理尺度、有效尺度和分辨率两类。DEM是表达地貌形态(地形)的最主要模型之一，DEM分辨率即为空间尺度之一，DEM分辨率尺度已经取得了一定的研究成果[3-7]。虽然基于DEM的地貌形态分形量化已经取得了较多的研究成果[8-23]，但是DEM分辨率对地貌形态三维分形量化的影响目前研究相对较少[12]，有待进一步研究，且已有的三维分形量化模型在模型结构及地形模拟方法上仍然存在有待改进的地方。另外，其他各种地形量化指标是否具有尺度效应也有待进一步研究。若某个地形量化指标具有尺度效应，使用该指标构建土壤侵蚀模型时，则应考虑地形尺度效应的影响。

综合以上分析，目前有两个问题亟待解决，一是地貌形态三维分形量化模型的改进，二是DEM分辨率对地貌形态三维分形量化指标及其他地形量化指标的影响。针对这两个问题，首先改进地貌形态三维分形模型，然后基于GIS组件开发技术、分形理论和改进的三维分形模型开发三维分形软件，进而对研究区不同尺度下的地貌形态特征进行三维分形量化，以期发现地形量化随DEM分辨率变化的规律。砒砂岩区二老虎沟流域是重力侵蚀和水力侵蚀都异常严重的交互侵蚀区域，对该区进行地貌形态量化的尺度效应研究可为该区土壤侵蚀模型的构建提供重要参考。

1　研究区概况

砒砂岩区二老虎沟流域位于内蒙古鄂尔多斯市准格尔旗沙圪堵镇，地理位置为110°35′—110°38′E，39°46′—39°48′N，面积6.3 km2，图1为该区无人机航拍影像。砒砂岩是古生代二叠纪、中生代三叠纪、侏罗纪和白垩纪的厚层砂岩和泥质砂岩组成的岩石互层，集中分布在内蒙古自治区鄂尔多斯市的东胜区、准格尔旗、伊金霍洛旗、达拉特旗、杭锦旗。按照地表覆盖物的不同，砒砂岩区可分为裸露砒砂岩区、覆沙砒砂岩区和覆土砒砂岩区。二老虎沟流域属于覆土砒砂岩区，砒砂岩在沟谷出露，形成“黄土盖帽，砒砂穿裙”的特殊地貌景观。该区土壤侵蚀以水蚀为主，水蚀、风蚀和重力侵蚀交替发生，属于土壤侵蚀异常严重地区。该区沟谷切割很深，呈V字型沟道，处在沟道侵蚀生长期。图2是研究区无人机航拍影像的局部，可以看出该区沟壑十分发育。

图1　研究区位置及无人机航拍影像　　　　　　　　　　　　　　　图2　研究区航拍影像局部

2　数据与方法

2.1多尺度DEM数据采集与数据处理

使用的DEM数据由无人机航拍结合摄影测量后期处理软件获得，采集的原始DEM数据为1 m分辨率。为研究不同尺度下的三维分形维数变化情况，对原始DEM数据进行重采样，分别生成2～32 m，间隔为1 m的32种分辨率的DEM数据。

构建的三维分形模型需要获取任意分形尺子下扫描盒子内的高程标准差和平均坡度数据。直接由扫描盒子内的高程数据提取坡度数据时，在扫描盒子边缘会产生误差。该误差源于DEM生成坡度数据时采用3×3窗口计算，且对边缘外围数据按无数据区处理。因此，需要采用另外一种数据处理方法：对各分辨率DEM先生成整个区域的坡度数据，并进一步将DEM和坡度数据进行波段合并以便于三维分形计算。在三维分形扫描时，直接提取分形盒子内的高程数据和相应坡度数据进行统计计算，避免了产生坡度误差，同时也降低了算法复杂度。限于篇幅，只给出1 m和32 m尺度的DEM与相应坡度的合成影像(图3—4)。

2.2研究方法

2.2.1分形理论

(1) 分形。1967年Mandelbrot[24]在美国《Science》上发表了一篇名为“英国的海岸线有多长？”的论文，给出了分形的最初概念。后来，英国数学家肯尼思·法尔科内[25]进行了补充，给出了较为合理的定义，他认为集F为分形，即认定分形具有下述性质：①F具有精细的结构，即有任意小比例的细节；②F是如此的不规则以至它的整体和局部都不能用传统的几何语言来描述；③F通常有某种自相似，可能是近似的或统计的；④ 一般F的“分形维数”大于它的拓扑维数；⑤ 在多数情形下F以简单的方法定义，可由迭代产生。

图3　1 m分辨率的DEM与坡度合成影像　　　　　　　　　　图4　32 m分辨率的DEM与坡度合成影像

(2) 分维。分维(fractal dimension)又叫分形维数，是分形理论中对非光滑、非规则、破碎的极其复杂的分形客体进行定量刻化的重要参数[22]。常见的分形维数有：豪斯道夫维数、容量维数、信息维数和关联维数等。其中容量维和信息维在地貌分形中应用较多。容量维是指用边长为r的规则盒子去覆盖测量，最后根据测量的盒子数来计算维数，即为容量维 ，公式为：

(1)

式中：N(r)——尺度为r下的盒子个数。

容量维只考虑了覆盖盒子个数，而没有考虑盒子内分形体的覆盖程度。通过统计分形体属于第i个盒子的概率改进容量维数测定方法，即可获得信息维数，公式为：

(2)

式中：pi——分形体属于第i个盒子的概率，其计算公式为：

(3)

式中：miri(r)——尺度为r下的第i个盒子内的地形起伏量；MIR(r)——三维实体在尺度为r特征尺度下的地面起伏总量，其计算公式为：

(4)

2.2.2地貌形态三维分形模型改进

(1) 地貌形态三维分形模型存在的问题。目前，地貌三维分形模型存在问题主要包括两个方面：一是模型中使用的地形模拟方法；二是三维分形模型结构问题。地形模拟方法主要有DEM、TIN、堆积立方体、三棱柱和四棱柱等三维模型。地形模拟使用立方体堆积表达地貌体，地形高程模拟不准确[14]，因为地貌某点的高程很少正好是立方体边长的整数倍。已有的三维分形模型结构也存在不合理性，如地形起伏量计算时使用了坡度标准差指标[22]。坡度标准差对于平斜坡地形不太合适，会导致计算的起伏量接近零，明显不合理。

(2) 解决方案。① 四棱柱模拟地貌体。为了便于三维分形扫描计算，有两种地貌体模拟方法，一种是采用堆积小立方体来模拟地貌体[14]，另外一种是使用四棱柱来模拟地貌体[22]。堆积立方体模拟方法对高程的模拟不准确，前节已说明原因。四棱柱模型可以准确地模拟地貌体高程，是较合理的模拟方法，适合选用。四棱柱模型就是以DEM像元为四棱柱底面，以DEM像元高程为四棱柱高度，由这些四棱柱排列组合来模拟地貌体；② 地形起伏量新指标——优化三维分形模型结构。目前常用三维分形信息维数对地貌进行量化。信息维数考虑了分形盒子内地形信息含量的不均性，能更准确地表达地貌复杂度信息。在三维分形信息维数测算中，涉及到分形盒子内地形起伏量计算。已有学者提出了测算公式，但有待改进。基于此，需要研究设计新的地形起伏量指标。

为了既能方便计算又能全面涵盖地形起伏信息，从地形量化单因子指标中选取若干个指标重组形成新的地形起伏量指标。单因子指标选择标准是既能准确量化、方便计算又能表达地形主要特征。在地形的常见单因子指标中，地形起伏度指标对地形的概括太强，不宜选用；沟壑密度指标不易准确确定，也不宜选用；坡度标准差对于平斜坡地形明显不适用，也不宜选用；而高程标准差和平均坡度对地形起伏描述较好，适合选用。

地球表面的地貌形态最核心特征概括起来无非是高低陡缓凹凸6种特征。因此基本可以概化为5种基本地形，以便进行深入探讨研究。为研究高程标准差和平均坡度指标表达地形起伏信息的侧重点，使用ArcGIS软件构建5种地形坡面，获取其DEM数据和坡度数据，并使用ArcGIS软件的区域统计功能对5种地形的高程信息和坡度信息进行统计。如表1所示，C地形的起伏量明显大于B地形，而B，C两种地形平均坡度基本相同，但C地形的高程标准差几乎是B地形的两倍，因此，把高程标准差作为地形起伏量的主控因子。A，B两种地形起伏量也应该是不同的，虽然具有相同的起伏高度，但A的起伏频率更大。A，B两种地形高程标准差相同，但平均坡度，地形A大于地形B。因此，平均坡度可以作为控制地形起伏频率的因子，称为地形起伏量的次级控制因子。高程标准差和平均坡度的乘积可以很好地区别A，B，C，D或A，B，C，E四种地形。因此，高程标准差和平均坡度的乘积可作为地形起伏的新指标。

表15种地形的高程信息和坡度信息统计结果

地形起伏量mir(r3)的计算是模型的关键，基于以上分析，使用新设计的地形量化指标作为地形起伏量的表达式，其计算公式为：

mir(r3)=std×α

(5)

式中：std——高程标准差；α——平均坡度。

2.2.3基于GIS组件技术的分形软件设计与实现

(1) GIS组件技术。GIS组件技术是近年来地理信息系统发展的趋势之一。ESRI ArcEngine是目前主流的GIS组件技术，其本身是一个COM GIS类库。该类库中提供了大量GIS组件对象，为GIS应用程序的开发提供了便捷方法。开发者只需根据应用的需要调用类库中的对象即可实现相应的GIS功能，可以把精力集中在应用模型的研发上。

(2) 基于ArcEngine的地貌形态三维分形扫描算法与实现。用边长为DEM像元宽度整数倍的正方体盒子(称为扫描盒子)对三维地貌体进行三维扫描。扫描盒子被全部填充的称为实体盒子，扫描盒子内包含地形表面的称为面盒子或特征盒子。

本模型只统计分形面盒子。三维扫描算法为：① 根据分形盒子边长将研究区划分成N×M个区域；② 对每个区域进行垂向扫描，统计扫描到的每个分形盒子内的高程标准差和平均坡度，计算该盒子内的地形起伏量，对地形起伏量进行累计；③ 改变分形尺子，执行1，2，3步；④ 所有区域扫描完毕后，计算地形信息总量，并对分形尺子对数和地形信息总量做线性回归分析，计算获得分形维数；模型使用ESRI ArcEngine组件技术实现，它其实是一个GIS类库。类库中的栅格游标对象RasterCursor以像素块(PixelBlock)为单位读取，一个像素块正好可以对应一个分形盒子。通过改变像素块大小对应分形尺子变化。通过栅格游标对象的IRasterCursor接口的next方法遍历像素块，进而实现每个分形盒子扫描。

3　结果与分析

3.1地貌形态三维分形多尺度量化

地貌形态分形量化中地形数据的尺度问题较少被考虑。众所周知，DEM地形数据具有尺度效应，基于不同尺度地形数据的量化结果不具有可比性。因此，非常有必要对地貌形态三维分形量化的尺度效应进行研究，以发现地貌形态分形量化变化规律。使用开发的地貌形态分形量化软件对32种分辨率的DEM地形数据进行地貌形态量化。由于随着分辨率的降低，DEM像元数减少，三维分形扫描中计算的分形盒子数量相应变少，地形表现出的统计自相似性减弱，因此，基于DEM直接重采样方法，这里只给出1～10 m尺度下的三维分形信息维数，其他尺度的地貌形态量化需要一定的处理方法，在后面一节讨论。

为了进行各尺度下三维分形维数的对比分析，分形尺子范围归一化为20～80 m，尺子间隔为一个像元大小。各尺度下的像元大小不同，尺子间隔亦不同。另外，受DEM像元大小的影响，分形尺子区间无法精确统一为20～80 m，取最接近区间。使用ArcGIS软件对其他地貌单因子量化指标也进行了1～10 m尺度的地貌形态量化，统计结果如表2所示。

表2不同尺度下的地貌多指标量化结果

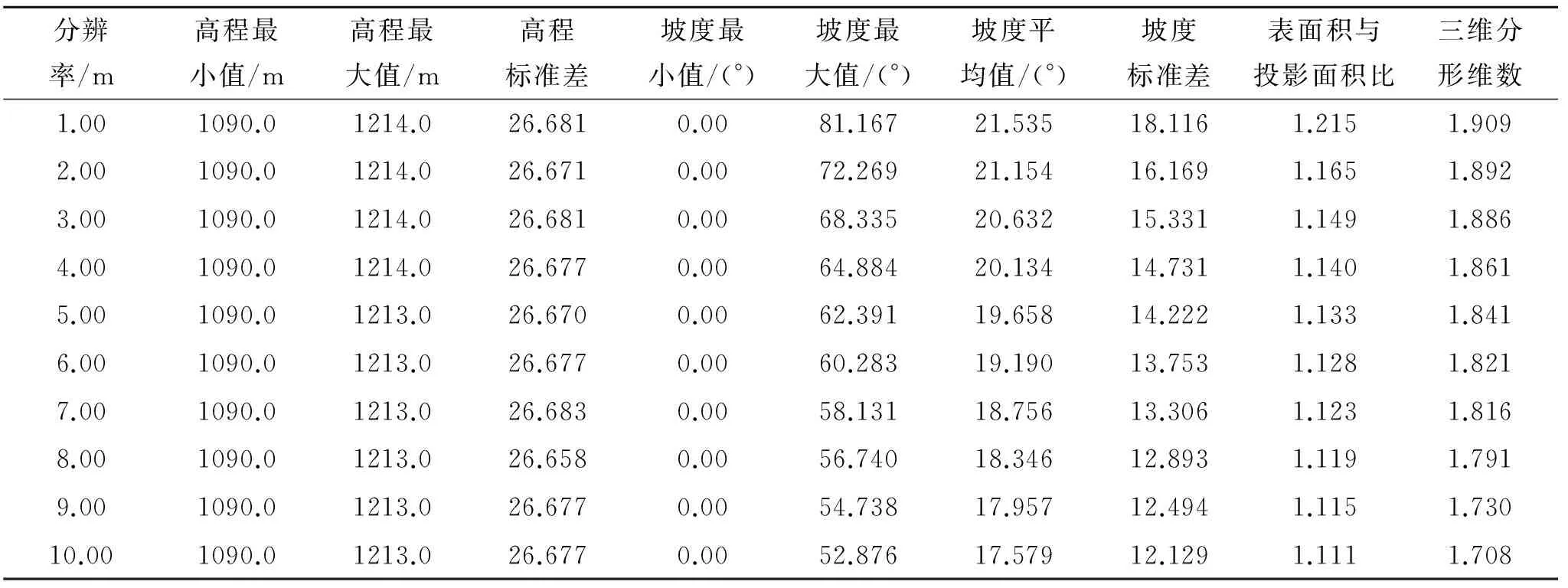
分辨率/m高程最小值/m高程最大值/m高程标准差坡度最小值/(°)坡度最大值/(°)坡度平均值/(°)坡度标准差表面积与投影面积比三维分形维数1.001090.01214.026.6810.0081.16721.53518.1161.2151.9092.001090.01214.026.6710.0072.26921.15416.1691.1651.8923.001090.01214.026.6810.0068.33520.63215.3311.1491.8864.001090.01214.026.6770.0064.88420.13414.7311.1401.8615.001090.01213.026.6700.0062.39119.65814.2221.1331.8416.001090.01213.026.6770.0060.28319.19013.7531.1281.8217.001090.01213.026.6830.0058.13118.75613.3061.1231.8168.001090.01213.026.6580.0056.74018.34612.8931.1191.7919.001090.01213.026.6770.0054.73817.95712.4941.1151.73010.001090.01213.026.6770.0052.87617.57912.1291.1111.708

3.2地貌形态三维分形量化的尺度效应

用DEM表达地形地貌本身就是对地形特征的一种简化，随着分辨率的降低所表达的地貌特征越来越概括，细节特征丢失的越来越多。地貌三维分形维数表达的是地形地貌的复杂度信息，从直观上来理解，三维分形维数也应随着地形尺度的增大而减小。事实是否与直观理解一样，减小的幅度有多大，有无明显拐点，有无最佳的地貌形态量化尺度，这些问题需要具体分析研究。根据三维分形测算结果，点绘于图上。如图5所示，随着DEM尺度的降低，三维分形维数呈线性降低趋势。三维分形维数从1.909迅速降低到1.708。从数值上看减小的不大，但是，事实上由于三维分形维数的区间主要是1.0～2.0，三维分形维数值减小0.2，对应的地形复杂度其实已经大大降低。

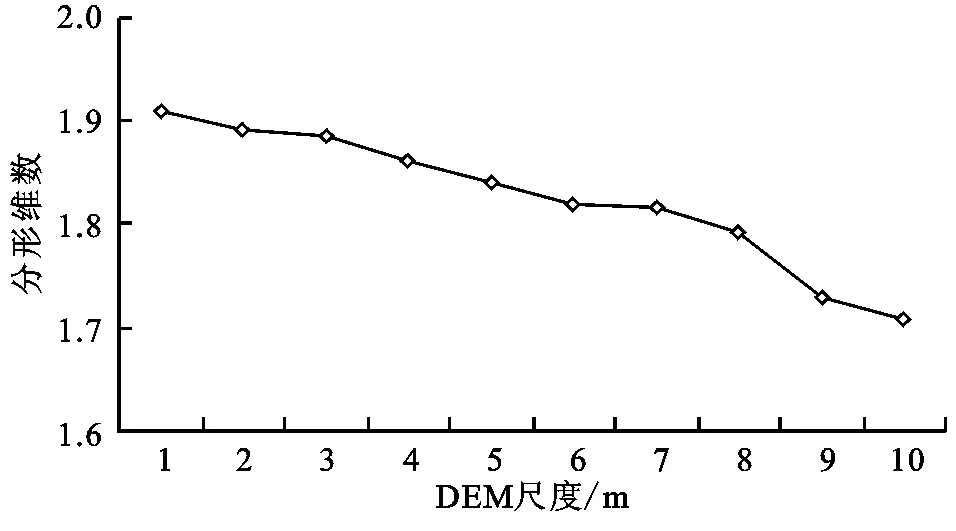
图5　不同尺度下的三维分形维数

为了研究地貌三维分形量化在20 m以上尺度的变化情况，并且要尽量的统一分形区间及分形尺子间隔，需要采取特殊的处理方法。成倍减小DEM像元边长且使用最邻近点重采样方法可使得各点的地貌高程在重采样过程中不发生变化。基于此，使用最邻近点重采样方法将2～32 m间隔为1 m的31种分辨率的DEM数据使用原像元边长的1/4大小进行重采样，使用重采样后的DEM构建四棱柱模型模拟地貌体，其模拟结果与原四棱柱模型相同，只是增加了四棱柱的数量。基于此方法，对各尺度下的地貌体分别进行三维分形量化。将量化结果点绘于图上。如图6所示，2～3 m尺度分形量化结果很接近，4～6 m尺度分形量化结果逐渐降低，7～11 m尺度分形量化结果基本保持在一个水平，分形维数区间为：1.967～1.981，12～22 m，尺度分形量化结果逐渐降低，23～32 m尺度区间分形量化结果为1.707～1.752，出现了波动现象，但地形复杂度已经大大降低。根据汤国安等[9]的研究成果，黄土沟壑区地形尺度阈值为5 m，结合研究区量化结果，3 m可作为该区最佳的地形量化尺度。

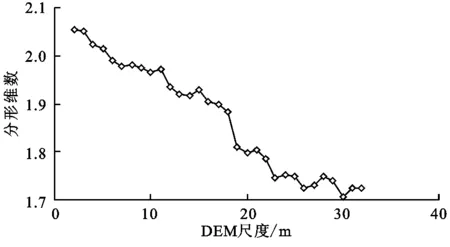
图6　缩四棱柱底面边长为1/4的多尺度分形维数

对其他地形量化指标也进行了尺度效应分析，将所有指标统计结果点绘于图上。如图7所示：① 三维分形维数和平均坡度尺度效应最明显，呈线性降低趋势，且二者的斜率几乎一致，因此，在地形量化中三维分形维数可近似用平均坡度来代替；② 坡度标准差和表面积与投影面积比指标也呈降低趋势，但基本呈凹形曲线，即降低得越来越慢；③ 高程标准差与高差基本不变，因此二者尺度效应不明显。

图7　多指标地貌形态量化尺度效应

综上分析，在地貌形态量化指标中，三维分形维数、平均坡度、坡度标准差及表面积与投影面积比4个指标具有尺度效应，高程标准差和高差两个指标不具有尺度效应。

4　结 论

针对目前地貌形态量化模型存在的问题，从地形模拟、模型优化两个方面提出了解决思路。研究认为：① 四棱柱模型模拟地貌体是较为适合三维分形计算的方法；② 新的地形起伏量指标可优化三维分形信息维数GIS模型。基于提出的地貌形态量化解决思路、GIS技术和分形理论，开发了地貌三维分形量化软件。使用该软件实现了砒砂岩区二老虎沟流域多尺度地貌特征量化。量化结果显示1～10 m各尺度的地貌三维分形量化区间为1.708～1.909，随着尺度的增加(DEM分辨率的降低)地貌三维分形维数呈线性降低趋势。砒砂岩区二老虎沟流域地貌三维分形量化最佳的地形尺度为3 m。在地貌形态量化指标中，三维分形维数、平均坡度、坡度标准差及表面积与投影面积比4个指标具有尺度效应，高程标准差和高差两个指标不具有尺度效应。前4个指标可称为地形复杂度指标，后两个指标称为地形起伏程度指标。

针对21～32 m尺度的DEM数据，为避免分形尺子间隔和分形区间差异过大，采用了降低四棱柱底面边长的方法。基于该方法对32种尺度地貌形态进行量化，结果显示：① 1～22 m尺度范围，三维分形维数整体呈线性降低趋势；② 23～32 m尺度范围三维分形维数出现抖动变化，原因有3个方面：采用了降低四棱柱底面边长模拟地貌体方法、分形盒子数量较少降低了地形统计自相似性以及分形区间不一致，哪个方面起主导作用，目前不易确定，有待进一步研究。

致谢：感谢国家地球系统科学数据共享平台——黄河下游科学数据中心为本论文提供数据支持。

[1]汤国安,刘学军,房亮,等.DEM及数字地形分析中尺度问题研究综述[J].武汉大学学报:信息科学版,2006,31(12):1059-1066.

[2]李霖,应申.空间尺度基础性问题研究[J].武汉大学学报:信息科学版,2005,30(3):199-203.

[3]刘学军,卢华兴,仁政,等.论DEM地形分析中的尺度问题[J].地理研究,2007,26(3):433-442.

[4]杨族桥.DEM多尺度表达研究[D].武汉:武汉大学,2009.

[5]宋小宁,李新辉.坡度的尺度效应及其对径流模拟的影响研究[J].地理与地理信息科学,2010,26(6):60-62.

[6]刘红艳.基于DEM的坡度尺度效应研究[D].陕西杨凌:西北农林科技大学,2011.

[7]郭伟玲.坡度和坡长尺度效应与尺度变换研究[D].北京:中国科学院研究生院,2012.

[8]McNab W H. A topographic index to quantify the effect of mesoscale landform on site productivity[J]. Canadian Journal of Forest Research,1993,23(6):1100-1107.

[9]汤国安,赵牡丹,李天文,等.DEM提取黄土高原地面坡度的不确定性[J].地理学报,2003,58(6):824-830.

[10]崔灵周,肖学年,李占斌.基于GIS的流域地貌形态分形盒维数测定方法研究[J].水土保持通报,2004,24(2):38-40.

[11]朱永清,李占斌,崔灵周,等.基于GIS流域地貌形态特征分形与计算方法研究[J].武汉大学学报:信息科学版,2005,30(12):1089-1091.

[12]朱永清,李占斌,鲁克新,等.地貌形态特征分形信息维数与像元尺度关系研究[J].水利学报,2005,36(3):333-338.

[13]Bolongaro-Crevenna A, Torres-Rodriguez V, Sorani V, et al. Geomorphometric analysis for characterizing landforms in Morelos State, Mexico[J]. Geomorphology,2005,67(3):407-422.

[14]朱永清.黄土高原典型流域地貌形态分形特征与空间尺度转换研究[D].西安:西安理工大学,2006.

[15]Papanicolaou A N T, Tsakiris A G, Strom K B. The use of fractals to quantify the morphology of cluster microforms[J]. Geomorphology,2012,139(2):91-108.

[16]Pelletier J D. Fractal behavior in space and time in a simplified model of fluvial landform evolution[J]. Geomorphology,2007,91(3):291-301.

[17]王民,李占斌,崔灵周,等.基于变分法和GIS的小流域模型三维地貌分形特征量化研究[J].水土保持学报,2008,22(4):128-131.

[18]Miliaresis G C. Quantification of terrain processes[M]∥ Zhou Q, Lees B, Tang G. Advances in digital terrain analysis. Berlin: Springer,2008.

[19]Martin E, John L. High resolution quantification of gully erosion in upland peatlands at the landscape scale[J]. Earth Surface Processes & Landforms,2010,35(8):876-886.

[20]Smith M J. Digital mapping: Visualisation, interpretation and quantification of landforms[J]. Geomorphological Mapping,2011,15:225-251.

[21]Hillier J K, Smith M J. Testing 3D landform quantification methods with synthetic drumlins in a real digital elevation model[J]. Geomorphology,2012,153(6):61-73.

[22]陶象武.基于GIS的流域地貌形态分形空间变异特征研究[D].北京:中国地质大学,2012.

[23]Siart C, Forbriger M, Nowaczinski E, et al. Fusion of multi-resolution surface (terrestrial laser scanning) and subsurface geodata(ERT, SRT)for karst landform investigation and geomorphometric quantification[J]. Earth Surface Processes and Landforms,2013,38(10):1135-1147.

[24]Mandelbrot B. How long is the coast of Britain? Statistical self-similarity and fractional dimension[J]. Science,1967,156(3775):636-638.

[25]肯尼思·发尔科内.分形几何:数学基础及其应用[M].曾文曲,译.沈阳:东北大学出版社,1991.

Multi-Scale Quantification of Topographic Feature Using Three-Dimensional Fractal Model and Its Scale Effect in Watershed—A Case of the Two-Tiger Valley of Pisha Sandstone Area

ZHANG Chuancai1,2，3, QIN Fen1，3, WANG Yongxin1,LIU Zhenzhen1, CHEN Yunsheng1, LIU Zhidan1

(1.CollegeofEnvironmentandPlanning,He′nanUniversity,Kaifeng,He′nan475004,China; 2.CollegeofSurveyingandMapping,AnhuiUniversityofScienceandTechnology,Huainan,Anhui232001,China； 3.KeyLaboratoryofGeospatialTechnologyfortheMiddleandLowerYellowRiverRegions,MinistryofEducation,He′nanUniversity,Kaifeng,He′nan475004,China)

Scientific quantification of topographic feature is one of the key issues in geomorphology and development of erosion model. In view of the existing problems on terrain simulation, geomorphology quantification model structure, geomorphology three-dimensional fractal model is optimized based on GIS and fractal theory, and topographic feature for Two-tiger valley in Pisha sandstone area is quantified based on multi-scale UAV DEM data and the fractal model, and scale effect of three-dimensional dimension on the area is discussed. The research found that: (1) as the topographic scale is reduced, three-dimensional fractal dimension decreases linearly, which means that terrain complexity decreases linearly; (2) terrain complexity under 10 m scale of Two-tiger valley is far less in Pisha sandstone area; (3) according to analysis on terrain quantification results based on multi index, terrain quantification indices can be divided into two types: terrain complexity index and terrain undulation index. The terrain complexity index has scale effect, and the terrain undulation index has no scale effect.

quantifying topographical character; Pisha sandstone; topographical three-dimension fractal; scale effect of landform

2015-02-08

2015-03-06

国家科技支撑计划项目(2013BAC05B01);国家自然科学基金项目(41401457)

张传才(1979—),男,山东梁山人,博士研究生,讲师,主要从事GIS与土壤侵蚀模型集成开发、虚拟地理环境研究。E-mail:zccai1205@163.com

P931.6

A

1005-3409(2016)01-0278-06