多普勒效应与观察者相对声源位置的关系

黄双印，郭振平

（延边大学理学院物理系，吉林延吉 133002）

大学生园地

多普勒效应与观察者相对声源位置的关系

黄双印，郭振平

（延边大学理学院物理系，吉林延吉 133002）

在时空图中，描绘出静止声源相位运动时空线和观察者运动时空线，用二条时空线的相交表示观察者对声信号的接收，并运用数形结合及数学解析的方法推导出多普勒效应的公式，公式表明多普勒效应不仅与观察者相对声源的速度有关，还与观察者相对声源的位置有关.

多普勒效应；相对位置；不共线；时空图

由于声源或观察者的运动而出现观测频率与波源频率不同的现象，称为多普勒效应［1-3］.目前，多普勒效应已在车速监测、医疗诊断和工程技术等各方面有着十分广泛的应用.然而，生活中物体的运动是复杂的，在实践中会发现若干新的问题，促使人们对多普勒效应不断进行着广泛的研究［4-15］.

文献［5-12］考虑了波的传播方向、波源速度、观察者速度三者不共线的一般情况，得到了适用范围较广的多普勒效应的普遍公式，揭示了多普勒效应既决定于观察者相对于介质的速度，又决定于声源相对于介质的速度.文献［13，14］通过分析计算发现：声波的多普勒效应不仅与速度有关，还与声源和观察者的相对位置有关.受此启发，本文将采用文献［15］给出的声源相位运动和观察者运动的时空线的描述方法，通过直观的几何认识再到简单的数学解析来对多普勒效应进行分析.

为了便于讨论，我们只考虑声源静止而观察者相对声源的运动情况.

1 观察者沿声波方向做匀速直线运动的多普勒效应

如图1所示，观察者相对静止声源匀速运动.S是声源，O是观察者，观察者与声源的初始距离为l，观察者的速度为u，声速为v.波动是振动在介质中的传播现象.对于声波，可认为每一个周期发出一个同相位信号.一系列的同心圆表示声源在每一个周期T内的等相位面.声信号的相位在静止空气中的传播和观察者的运动在时空图中的描述如图2所示.以声源S的位置为坐标原点，横轴x表示观察者离声源的距离，纵轴t表示时间.射线S0、S1、S2、…表示声源在0、1T、2T、…时刻发出的信号在静止空气中的传播，其中T表示声源振动所发出的声波周期.射线OA′表示观察者在时空中的运动，A点表示观察者接收到声源发出声信号的第一个相位，B点表示观察者接收到声源发出声信号的第二个相位，则观察者接收到声信号的周期T′=tB-tA，观察者接收到声信号的频率v′=1/T′.

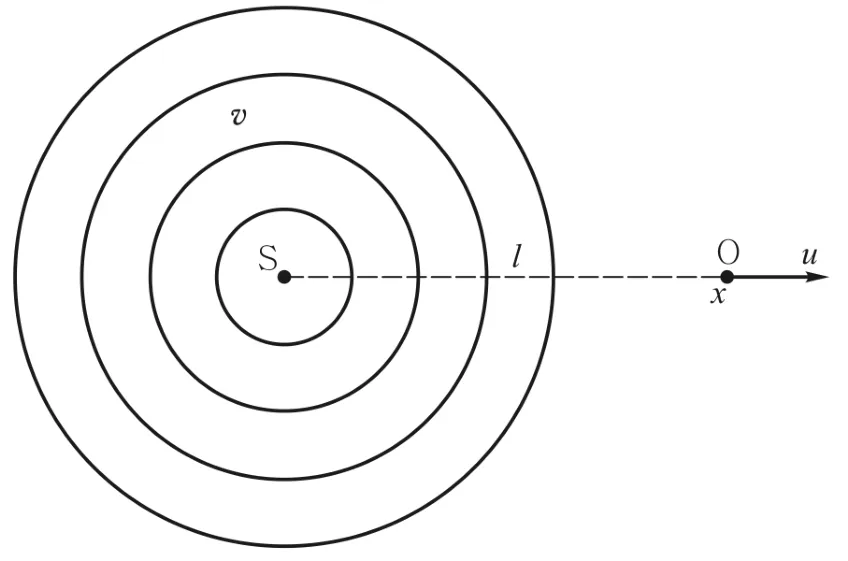
图1 观察者相对静止声源匀速运动

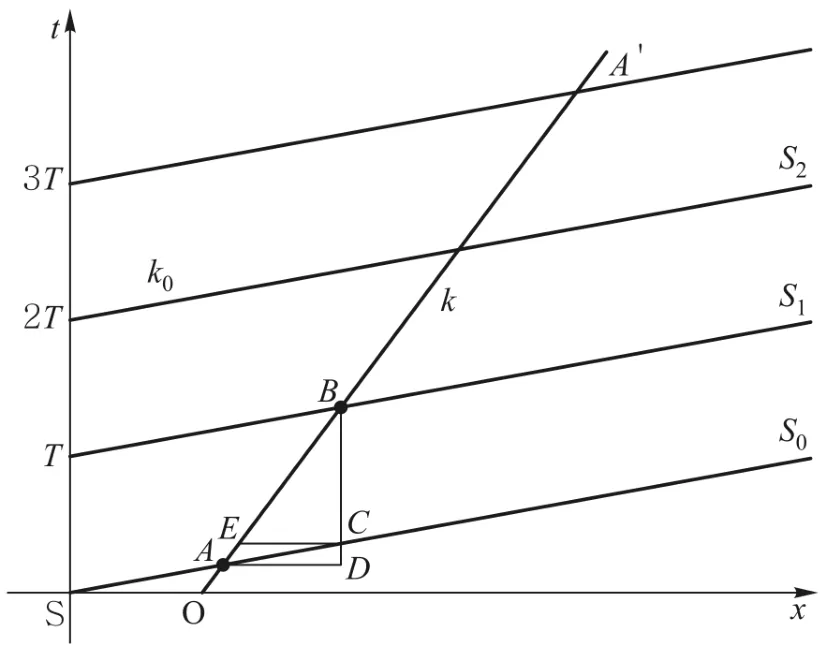
图2 用时空图描述声信号的传播和观察者的运动

从图2中的一系列交点可以看到T′不随位置和时间的改变而改变，只和直线的斜率有关，也就是说T′只和观察者相对声源的运动速度有关.令直线SA的斜率为k0，射线OA′的斜率为k，这两类直线可分别称为声源相位运动时空线和观察者运动时空线［15］，它们的斜率分别表征了声波的速度的倒数和观察者运动速度的倒数.图2中线段AD为AB在Ox轴上的投影.连接BD与声源相位运动时空线SA交于C点，过C点作AD的平行线与AB相交于E点.显然，BC=T，BD=T′，根据两个三角形ΔADC与ΔADB之间的几何关系不难看出：

式（3）就是一般文献中所讨论的观察者沿声波传播方向远离声源运动时的多普勒效应公式.要求u＜v，且靠近声源时u为负值，远离声源时u为正值.式中ν=1/T为声源的振动频率.

2 观察者不沿声波方向做匀速直线运动的多普勒效应

生活中，当观察者接收声源发出的声信号时，观察者的运动并不一定恰好沿声波传播方向，而是与声波方向成一定角度θ，如图3所示.设观察者的运动方向所在直线与声源的垂直距离为d，x表示任意时刻观察者与声源的距离，u表示观察者运动的速度（u＜v且靠近声源时u为负值，远离声源时u为正值），l表示在运动方向上离声源的初始距离.由几何关系得出：（当观察者靠近声源时，t∈［0，l/u］；当观察者远离声源时，t∈［0，∞］）.

图3 观察者与声源成一定角度运动

此时，声信号的相位在静止空气中的传播和观察者的运动在时空图中的描述如图4所示.从图4的一系列交点可以看到T′随着位置和时间的改变而改变，即观察者不沿声波方向做匀速直线运动时，所接受到的频率或周期随观察者相对声源的位置的变化而变化.下面，分别从声源的振动周期比较小和声源的振动周期比较大的两种情况进行探讨.

图4 观察者不沿声源方向做匀速运动的时空图描述

2.1 当声源的振动周期较小时的多普勒效应

当声源的振动周期比较小的时候，声源相位运动时空线比较密，图4中两个交点之间的斜率k1、k2、k3、…、kn、…可近似看成观察者的运动曲线的时间t对距离x的导数，即

当d＜＜x或θ很小时，可用kn代替式（1）的k，下式近似成立：

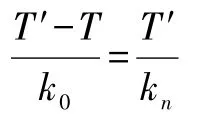
由此得

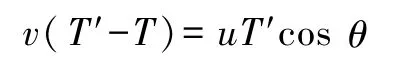
即

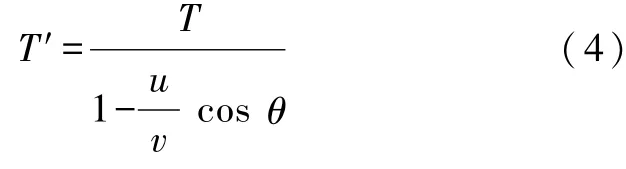
或

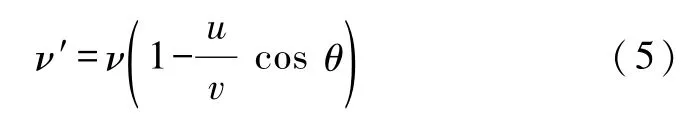
式（5）表明：在声源的振动周期和观察者的运动倾角θ比较小的情况下，多普勒效应公式（3）中的观察者的运动速度应替换为观察者的运动速度在观察者与声源连线方向上的分量.然而，这个方向是随时在变化的，即角θ是变量.可见多普勒效应与观察者的位置有关.

2.2 当声源的振动周期较大时的多普勒效应

当声源的振动周期比较大的时候，观察者时空线的斜率kn不能用代替.考虑观察者时空线和声波时空线的交点恰为接收同相位信号的时刻和空间位置，可由直线系的交点法确定T′.由于相邻的声波时空线的时间间隔为T，射线S0、S1、S2、…可写成直线系方程：

观察者的运动方程可以表示为

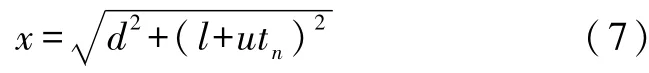
联立式（6）和式（7），求解一元二次方程可以解出

相邻的交点对应的时刻之差即为观察者接收到声信号的周期，即

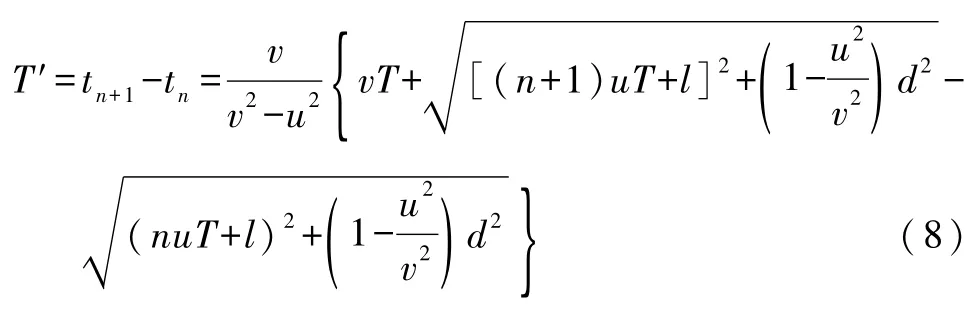
（式中n=0，1，2，3，…，u＜v且靠近声源时u为负值，远离声源时u为正值）

考虑T很大，满足nuT+l＞＞d，可对式（8）的平方根作级数展开，取一级近似得出

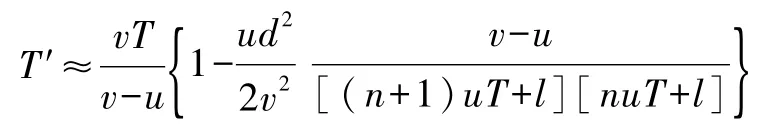
再考虑u＜v，上式中最后一项的值远小于1，可近似得出观察者接收到声信号的频率为

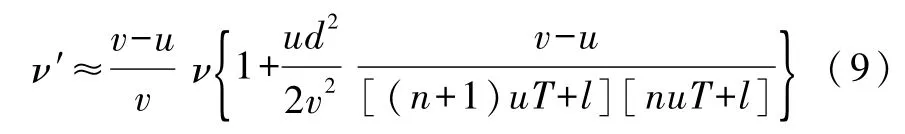
当取d=0时，式（9）过渡到观察者沿声波方向做匀速直线运动时的多普勒效应公式式（3）.可见，当d≠0时，即观察者不沿声源方向做匀速直线运动时，观察者接收声信号的周期和频率不仅取决于波速和观察者的运动速度，而且与观察者的相对位置有关，并非将观察者的运动速度在观察者与声源连线方向投影即可.

3 结论

通过运用数学解析的方法，求解静止声源相位运动时空线和观察者运动时空线的一系列交点，得出当观察者沿着声源方向运动时，多普勒效应与二者的相对速度有关；当观察者不沿着声波方向运动时，多普勒效应不仅与二者的相对速度有关，还与二者的相对位置有关.

［1］漆安慎，杜婵英.普通物理学教程：力学［M］.3版.北京：高等教育出版社，2012.

［2］赵凯华，罗蔚茵.新概念物理教程：力学［M］.2版.北京：高等教育出版社，2004.

［3］张汉壮，王文全.力学［M］.3版.北京：高等教育出版社，2015.

［4］钟锡华.多普勒频移的普遍公式［J］.大学物理，1995，14（10）：16-18.

［5］赵凯华.不同参考系中多普勒效应公式的统一［J］.大学物理，2006，25（7）：1-3.

［6］赵永泉.由相位不变原理讨论机械波的多普勒效应［J］.大学物理，1995，14（3）：43-44.

［7］路峻岭，汪荣宝.多普勒效应公式的简便推导［J］.大学物理，2005，24（8）：25-27.

［8］高炳坤，王凤林.相对论多普勒效应的简易推导［J］.大学物理，2003，22（8）：15-18.

［9］魏国柱，李林，杜安.普遍情况下的多普勒效应表达式［J］.东北大学学报，2004，25（6）：602-605.

［10］贾湘平.多普勒效应探讨［J］.辽宁工业大学学报，2011，31（6）：395-397.

［11］陈光平，祝恒江.多普勒效应公式的系统推导方法［J］.广西物理，2005，26（4）：41-44.

［12］李崇虎.适用于不同条件的多普勒效应公式［J］.西南师范大学学报，2007，32（2）：145-148.

［13］郑世宁.多普勒效应之拙见［J］.大学物理，1996，15（3）：16-17，24.

［14］张寅静，凌虹.关于任意方向多普勒效应的研究［J］.河南教育学院学报，2003，12（1）：13-15.

［15］王克勋.用时空线分析多普勒效应［J］.大学物理，1997，16（12）：8-11.

Relationship between the Doppler effects and the position of observer to sound source

HUANG Shuang-yin，GUO Zhen-ping
（Department of Physics，College of Science，Yanbian University，Yanji，Jilin 133002，China）

In the space-time diagram，use the space-time lines to describe the movement of the static sound phase and the observer，and the intersection of two lines means the observer receives the sound signal.Combining mathematical graph，we analysis to deduce that formulas of the Doppler effects，those are not only associated with the speed of the observer to the sound source，but also related to the position of the observer to the sound source.

Doppler effects；position of observer to sound source；non-collinear；space-time diagram

O 412.1

A

1000-0712（2016）05-0046-04

2015-08-26；

2015-11-17

高等学校力学课程教学研究项目（JZW-15-LX-14）、吉林省高等教育学会重点课题（JGJX2015B7）、吉林省教育科学规划课题（GH150040）、延边大学大学生创新创业训练计划项目（ydbksky2015385）资助

黄双印（1993—），男，江苏淮安人，延边大学物理系2012级本科生.

郭振平，E-mail：gzpllwl@ybu.edu.cn