再制造流程中旧件回收策略

艾伦

（同济大学　经济与管理学院，上海　200092）



再制造流程中旧件回收策略

艾伦

（同济大学经济与管理学院，上海200092）

回收旧件的质量对于再制造商来说有很重要的作用，高质量的旧件能够为再制造商带来更多的利益。为了鼓励消费者能够返还高质量的旧件，再制造商往往会在销售商品的时候向消费者收取一定的押金，押金会根据旧件质量的好坏全额或者部分返还。考虑再制造商通过构建旧件回收策略对该再制造商产品的旧件根据质量的不同进行回收，提出两种不同的旧件回收策略，并分析押金以及旧件质量的变化对再制造商回收策略的影响。

再制造；旧件；回收策略；押金

1　引言

再制造就是将回收的旧件进行重新翻新、修理，使其能够达到新产品的标准并作为新产品重新投入到市场中进行销售的过程。再制造作为闭环供应链的一部分，包括了许多个环节，比如回收、检测、分级、报废处理、再制造。许多产品如汽车蓄电池、打印机、电脑等都可以进行再制造的销售Samar K M，Huafan Ma.（2009）［1］。Kelindorfer，et al.（2005）［2］对一些相关问题进行了综述，总结了过去关于可再生资源运营管理的文献，他们将这些生产运营管理领域的文章主要分为三个方面，第一个方面为绿色产品以及流程发展，第二个方面是精益与绿色运营管理，第三个方面是再制造与闭环供应链。

在再制造流程中，当一个再制造商向消费者售出一个商品时，再制造商往往会向消费者收取一定的押金鼓励消费者将商品的旧件进行回收。在实际生活中，这种情况最常见的就是饮料的销售，当消费者购买饮料时，会被收取一定的费用作为饮料瓶的押金，商家希望通过押金来回收可以循环利用的饮料瓶，当消费者将饮料瓶完好的退还给商家时，之前被收取的押金就会全部返还给消费者。在一些其他的情况下，再制造商会根据退还旧件的产品质量来确定需要退还的押金数额。Wei S，et al.（2014）［3］着重于在根据回收产品的质量对消费者进行资金偿还。文章为再制造商设计了三种资金偿还政策以及在每种资金偿还策略下的再制造商利润模型，给出了回收件质量服从正态分布时每一种资金偿还模型的最优解。通过数值分析提出了在整个模型中，消费者对于回收件价值的评价是整个模型的重要影响因素，同时比较了押金返还政策与信用政策的比较。

因为旧件的质量存在很大的不确定性，除了在返还旧件时会根据旧件的质量进行返还，一些学者还着重研究了旧件在进入再制造流程前是否需要根据质量进行分类的必要性。Ferguson，et al.（2009）［4］研究了当回收的旧件具有不同的质量等级时的生产计划问题，他们观察到将回收旧件进行分类并且将其放在不同的库存中将会提高再制造商的利润，对一个多等级的排队系统进行了仿真，建立了一个拥有多个工作站的再制造系统。不同质量旧件的再制造成本和在工作站上的工作时间会不同，因此旧件质量检测中存在的误差会影响整个系统的内在表现。Guide，et al.（2005）［5］研究了在一个实际的再制造过程中，对于产品回收的实时信息影响。文章中使用了一个粗略的估计来评价在供应链的前端采取一个快速的产品分类带来的成本降低。同时，整个模型也是在对回收件的分类上没有误差。Ketzenberg，et al.（2006）［6］通过比较在进行旧件回收前获得的信息量不同的模型，研究了信息对于需求、回收率、运营成本的影响。他们的研究提供了假设再制造产品的需求函数服从正态分布。Robotis，et al.（2012）［7］对比了两种极端检测环境下的情况，第一种情况是再制造商没有能力对收的旧件进行质量检测，所以所有回收的旧件都进行了再制造，另一种情况是再制造商有能力对回收件进行没有误差的检测，只有具有较低再制造成本的旧件才会被进行再制造。Niknejad and Petrovic（2014）［8］考虑了一个混合的制造与再制造系统，旧件的质量决定于一个离散的分级系统所进行的质量分级，然后，不同等级的旧件将会根据之前所制定的分级指标被分配到不同的再制造路径。Panagiotidou，Nenes and Zikopoulos（2013）［9］研究了一个产量信息取决于对所有回收件的抽样检查。虽然对于回收件的评价是准确的，单回收件的数量是会出现误差的，这个误差是由于样本的统计误差所引起的。Van Wassenhove and Zikopoulos（2010）［10］研究了在随机的回收量以及多个供应商的情况下的再制造问题，这其中，供应商将会对回收旧件的分类错误负责。Galbreth and Blackburn（2006）［11］解决在再制造旧件回收中，在旧件质量的分类没有误差发生的情况下，再制造商的最优回收量。结果表明越大的旧件回收量将会帮助再制造商有更大的灵活性采用更高质量的回收件进行再制造来满足市场的需要，同时降低再制造成本。同时该文章研究指出对回收旧件进行分级的过程是没有误差产生的。

本文在前人研究的基础上，将押金返还策略与旧件质量检测相结合，构建再制造商最优的旧件回收策略。

2　基本模型

2.1模型假设

本文的模型中，一个再制造商销售一种只含有一种元件的商品，市场中不存在类似产品的竞争与替代。因此再制造商需要回收的旧件仅是一种元件，消费者在购买该商品时，再制造商对每一件商品需要向消费者收取一定的押金，消费者在返还该旧件时，再制造商会根据不同的策略来返还相应的押金。回收的旧件会进入再制造商的再制造流程进行再制造。

模型中引用的变量如下：cm是利用旧的元件制造一单位新产品的成本，c是再制造商利用新的元件制造一个单位新产品的成本，w1表示再制造商实施单一押金返还策略时的利润，w2表示再制造商实施根据质量返还押金策略下的利润。产品的单位售价为p。D（x）表示制造商的需求函数，其中x表示再制造商售出一件商品向消费者收取的押金。本文假设回收旧件的质量密度函数为 f（q），累积密度为F（q）。旧件的质量q∈［0，1］，q=0表示回收的旧件没有任何的价值，再制造成本与重新生产一个产品的成本一样，q=1表示回收旧件的质量与新件的质量完全一样，这种情况下，再制造成本为0。

本文假设再制造商产品的市场需求函数如下：

因为再制造商在销售产品时会向消费者收取一定数额的押金，由于本文假设该市场中不存在相似产品的替代，因此本文假设再制造商产品的需求量受到了所收取押金的影响。本文考虑两种不同形式的市场需求函数，线性需求函数：D（x）=D0-βx，其中 β＞0，当x=0时，产品市场需求为D0；指数型需求函数：D（x）= D0e-αx，其中α＞0，当x=0时，产品的市场需求为D0。在两种模型下，随着收取押金数额的增大，产品的需求量都会降低。

再制造商对同一个产品拥有一个单一的再制造流程，如果回收的旧件质量太差，进行再制造对于再制造商来说没有任何的利益时，这些旧件将不会进行再制造，再制造商需要对这些没有再制造意义的旧件进行销毁，所以对于再制造商现有的再制造技术来说，存在一个可进行再制造旧件的质量下限qˉ，当回收的旧件质量q＞qˉ时，旧件统一进入一个再制造流程，所有旧件都要通过同样的再制造流程后作为再制造新品进行再次销售，因此，本文假设进入该再制造流程的所有旧件的再制造成本相同，并且与再制造商设定的回收旧件进行再制造的质量下限有关，本文假设旧件进行再制造的成本为是缩放系数，c是重新生产一个新产品的成本，这个模型表示，企业设定的可进行再制造旧件质量的下限越高，旧件的再制造成本越低。整个流程大致为：（1）再制造商销售产品，每件产品向消费者收取一定的押金。（2）再制造商进行废旧产品元件的回收，根据元件的质量情况依据不同的政策给予消费者全额或者部分押金的返还。（3）再制造商进行再制造，然后销售产品。由于本文假设市场中不存在相似产品的替代性，因此，为了获得期初向再制造商支付的押金，购买了产品的消费者都会愿意选择向再制造商返还旧件。

2.2模型的构建

第一种情况是单一的押金返还策略：在这种情况中，对于所有返还的旧件，不论质量的高低，再制造商都会全额返还销售产品时向消费者收取的押金。再制造商的总收益为：

第二种情况是根据质量返还押金策略：再制造商在收到消费者返还的旧件时，对旧件进行大致的检验以确定该旧件是否能够进行再制造，单位检测成本为s。如果旧件的质量低于可进行再制造的质量下限qˉ，那么再制造商就不会回收该旧件，经过大致的检验，如果该旧件可以进行再制造，在根据质量返还押金的策略下，再制造商返还的押金完全根据消费者对于该旧件的心理评估进行返还，因此，在该策略下，再制造商的总收益为：

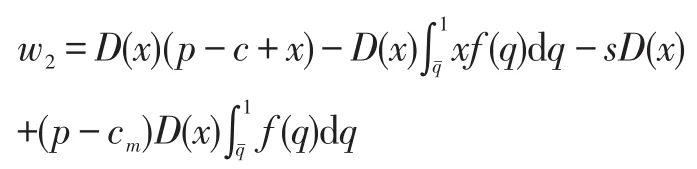
3　消费者价格敏感性分析

在两种押金模式中，根据本文的假设，产品的市场需求与再制造商向消费者收取的押金数额有关，因此再制造商向消费者收取押金时需要考虑押金的数额对于需求的影响，文章这部分将要分析一下在不同的押金返还策略中，押金的数额对于再制造产品需求量的影响。

在单一的押金返还策略中：

即：

在根据旧件质量进行押金返还的策略中，

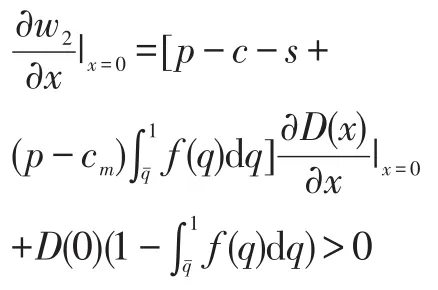
即：

根据以上分析，在需求函数中，α与β体现了消费者对于再制造商品的需求敏感性，再制造商如果要对消费者收取押金，必须考虑消费者对于押金的敏感性大小，否则，通过向消费者收取押金来促使消费者返还旧件的策略不会为再制造商带来收益的增加。

4　在质量呈均匀分布的情况下，再制造商回收策略的数值分析

均匀分布具有显著的不确定性，可以用来描述再制造过程中回收旧件的质量分布，本文假设回收旧件的质量q在［0，1］上呈均匀分布，即：f（q）=1，q∈［0，1］。再制造商回收旧件的初衷是通过再制造带来收益，因此，再制造商利用旧件生产一个再制造新品的完全成本小于重新生产一个新产品的成本，在本文的模型中，回收旧件的质量q∈［0，1］，质量在0到1上呈均匀分布，q=0，即回收的旧件没有任何利用价值，q=1，即回收旧件的质量可以完全等同于新产品，进行简单的清洗与包装就可以再次进行销售，再制造成本几乎为0。

在下面的算例分析中，本文对各个参数做出如下的假设，qˉ=0.6，D0=1 000，p=2，c=1，μ=0.5，cm=0.7，cr=0.5，s=0.5。根据之前对于需求函数系数α和β需要满足的条件，假设α=0.5，β=500。

当市场需求函数为线性关系时，即D（x）=D0-βx，在单一押金返还策略中，再制造商的利润与押金关系如图1所示。

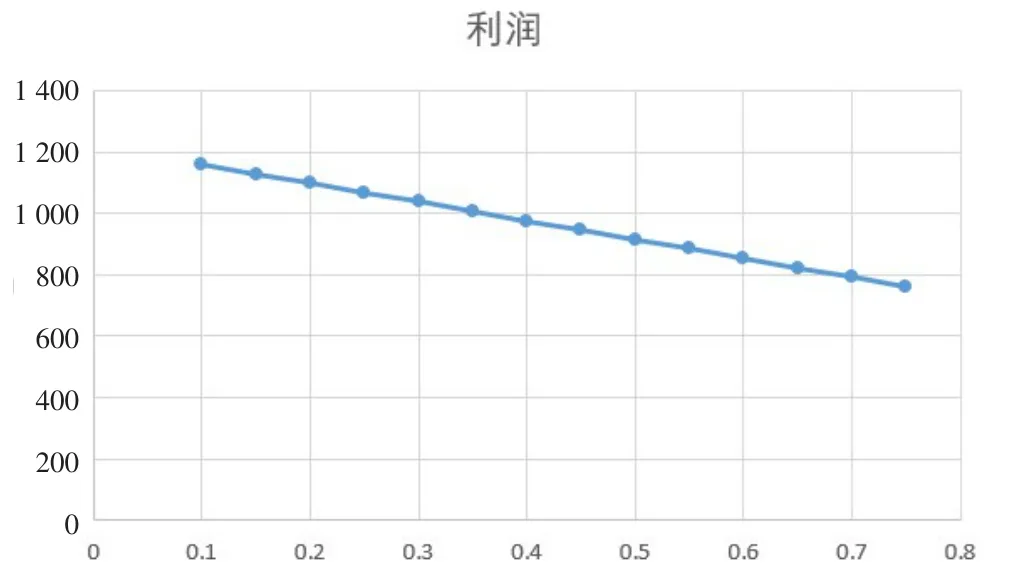
图1　单一押金策略下利润与押金关系图

在单一押金返还策略中，当其他变量确定的情况下，再制造商的利润与收取的押金呈线性函数，且随着押金的增大，再制造商的利润降低，因此再制造商在单一押金返还策略下，最优的策略就是不收取押金。但是在该模型中，再制造商可以通过改变自己的再制造工艺，通过提升再制造技术，有效降低再制造的成本，从而降低可以进行再制造的回收旧件的质量下限。假设再制造商对于每一件商品所收取的押金为0.5，再制造商的利润与设置的可进行再制造的旧件质量下限的关系如图2所示。

从图2可以看出，在单一押金返还策略下，如果再制造商确定了对于每件商品收取的押金数额，通过改变再制造流程，提高再制造技术，降低可进行再制造旧件的质量下限，可以有效的提高再制造商的利润。

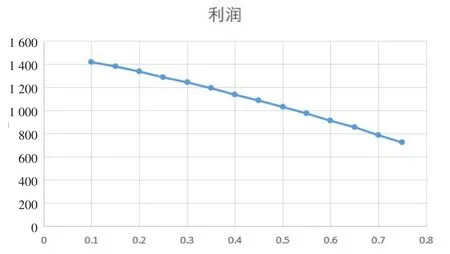
图2　单一押金策略下利润与质量下限关系图

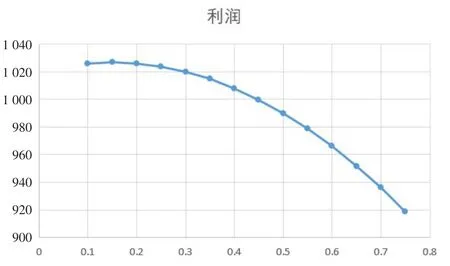
图3　根据质量返还押金策略下利润与押金关系图

在根据质量返还押金策略中，再制造商的利润与押金的关系如图3所示。

根据图3，可以看出再制造商的利润会先随着收取押金的增大而增大，然后会逐渐减少，因此在根据旧件质量返还押金的策略下，再制造商存在最优的收取押金的数额。由根据质量返还押金策略中的利润函数：

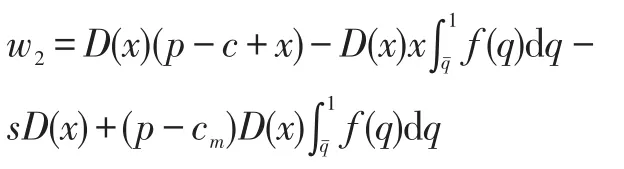
可知，旧件的检测成本过大，那么采取这样的押金策略不会为再制造商带来收益。当再制造商确定对每一个商品收取的押金数额一定时，再制造商的利润与可进行再制造旧件的质量下限的关系如图4所示。

由图4可知，在这个旧件回收策略下，通过提高再制造流程工艺，降低可进行再制造旧件的质量下限，再制造商可以提高利润。在指数关系下的商品需求函数与线性关系类似，本文将不再进行相似的数值分析。

5　结论

在再制造商回收旧件的闭环供应链系统中，本文考虑了再制造商通过收取押金来鼓励消费者返还旧件，从而再制造商可以通过对旧件的再制造来获得利益。本文考虑了再制造商运用两种不同的押金返还策略进行旧件的回收，并给出了不同情况下再制造商需要采取的策略。押金数额以及再制造商设置的可进行再制造的质量下限对于再制造商利润的影响。

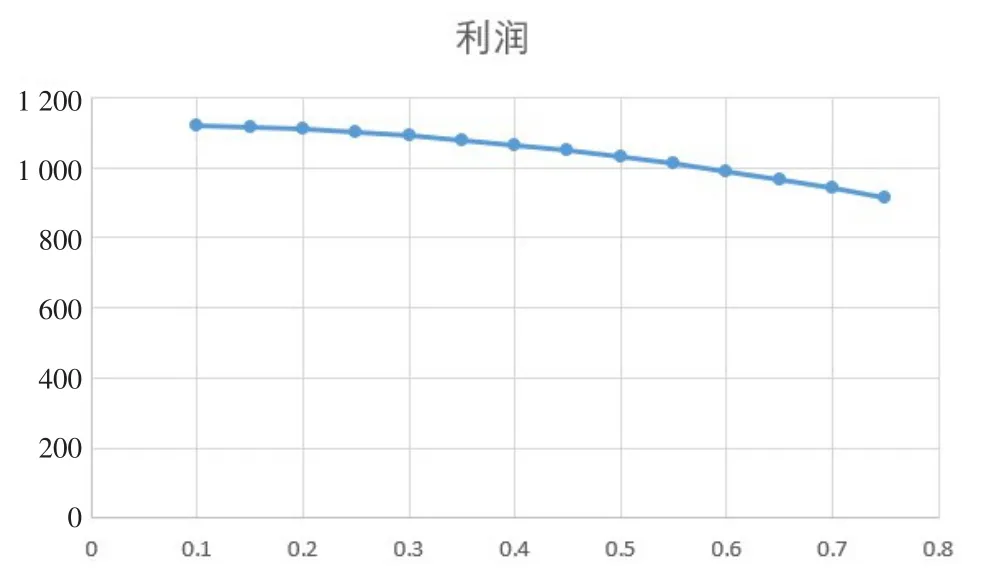
图4　根据质量返还押金策略下利润与质量下限关系图

但是，文章模型中简化了许多细节，还存在着许多的不足，对于该课题进行更深入研究可以围绕以下两个方面来进行：

（1）根据质量返还押金的策略中，旧件的检测存在质量的偏差，在实际中，完全根据旧件质量来进行押金的返还是不能够达到的，检测成本投入越大，旧件的检测精度越高，再制造商越能够做出准确的决策。在理想的状况下，不同质量旧件的再制造成本存在差异，从而在再制造流程中会造成再制造成本的增加，如何平衡旧件检测成本与旧件的再制造成本是需要考虑的一个问题。

（2）当市场中存在竞争时，消费者会根据旧件的市场价格与再制造商的预期返还押金数额做出比较来决定是否返还旧件。

［1］Samar K Mukhopadhyay，Huafan Ma.Joint procurement and production decisions in remanufacturing under quality and demanduncertainty［J］.InternationalJournalOfProduction Economics，2009，（1），5-17.

［2］Kleindorfer P，Kaylan S，van Wassenhove.Sustainable operations management［J］.Production And Operations Management，2005，14（4）：482-492.

［3］Wei S，Tang O，Liu W.Refund pricing policies for cores with qualityvariationinOEMremanufacturing［J］.International Journal Of Production Economics，2014，115：424-432.

［4］Ferguson M，Guide Jr V D，Koca E，Van Souza G，C.The value of qualitygrading in remanufacturing［J］.Production and Operations Management，2009，（18）：300-314.

［5］Guide Jr V D R，Muyldermans L，Van Wassenhove L N. Hewlett-packard company unlocks the value potential from time sensitivereturns［J］.Interfaces，2005，35（4）：281-293.

［6］Ketzenberg M E，Van der Laan E A，Teunter R H.Value ofinformation in closed loop supply chains［J］.Production and Operations Management.2006，15（3）：393-406.

［7］Robotis A，Boyaci T，Verter V.Investing in reusability of products of uncertainremanufacturing cost：The role of inspection capabilities［J］.International Journal Of Production Economics，2012，140：385-395.

［8］Niknejad A，D prtovic.Optimization of integrated reverse logistics networks withdifferent product recovery routes［J］.European Journal Of Operational Research，2014，（1）：143-154.

［9］Panagiotidou S，G Nenes，C Zikopoulos.Optimal procurement and productiondecisions under stochastic yield of returns in reverse supply chains［J］.OR Spectrum，2013，35（1）：1-32.

［10］Van Wassenhove L N，C Zikopoulos.On the effect of quality overestimation in remanufacturing［J］.International Journal Of Production Research，2010，48（18）：5 263-5 280.

［11］Galbreth M R，Blackburn J D.Optimal acquisition and sorting policies forremanufacturing［J］.Production And Operations Management，2006，（15）：384-392.

Study on Strategy of Old Parts Recycling in Remanufacturing Process

Ai Lun
（School of Economics Management， Tongji University， Shanghai 200092， China）

To encourage consumers to recycle high-quality old parts， remanufacturers usually collect a certain amount of deposit fromthe consumers when selling them the commodities and repay them in full or part in view of the condition of the old parts returned. In thispaper， in view of a remanufacturer that recycled old parts according to their quality， we proposed two different recycling strategies and thenstudied the influence of the deposit and old part quality on the strategy of the remanufacturer.

remanufacturing； old part； recycling strategy； deposit

F713.2；F252.19

A

1005-152X（2016）08-0097-05

10.3969/j.issn.1005-152X.2016.08.025

2016-07-07

艾伦（1991-），男，四川成都人，同济大学经济与管理学院硕士研究生，研究方向：供应链管理。