基于延迟均衡的CO2两相引射器模型研究

何 阳　张早校,　薛长乐　张亚洲　邓建强

(1 西安交通大学动力工程多相流国家重点实验室　西安　710049；2 西安交通大学化学工程与技术学院　西安　710049)



基于延迟均衡的CO2两相引射器模型研究

何 阳1张早校1,2薛长乐2张亚洲2邓建强2

(1 西安交通大学动力工程多相流国家重点实验室西安710049；2 西安交通大学化学工程与技术学院西安710049)

引射器对跨临界CO2引射制冷系统性能有极大的影响。本文考虑CO2两相引射器中存在的非平衡相变、超音速和壅塞等复杂流动现象，构建了CO2两相引射器的1D分布模型，并采用延迟均衡理论分析喷嘴中的非平衡相变过程。与实验结果比较显示，所建立的延迟均衡模型能够很好的预测引射器的性能。此外，通过与均衡模型的相比显示，在本文所选工况下，延迟均衡模型计算所得的主动流流量比均衡模型预测值低12.39%～25.30%，同时非平衡现象将延缓喷嘴中的膨胀过程，使得喷嘴出口压力比均衡模型预测值高。本文采用所建模型进一步分析了引射器的结构对性能的影响，结果显示在一定的工况下存在最优的混合室直径使得引射系数和升压比都较高；而当混合室直径一定时，较长的混合室有利于提高引射器的升压比。

两相引射器；延迟均衡模型；非平衡相变；CO2

引射器作为跨临界CO2引射制冷循环的重要部件，对系统性能的提高有重要作用[1-3]。李倩等[4]的研究表明相同工况下，跨临界CO2引射循环比传统循环的COP最大高14%。而徐肖肖等[5]针对带引射器的CO2热泵热水器的实验研究显示，引射器能够明显地提高系统的制热系数。任立乾等[6]通过对喷嘴结构的改善使得R134a系统的COP提高了12%。相似地，Banasiak K等[7]针对CO2引射制冷系统的实验研究也显示，引射器的结构优化有助于显著提高系统性能及引射器的工作效率。然而，CO2引射器内部流场复杂，目前尚没有一个成熟的理论模型指导CO2引射器的结构优化设计。

根据He S等[8]总结的各种引射器模型，目前已发展的1D引射器模型大多基于均衡流体假设，依据质量、动量、能量守恒理论建立，将各种损失归结于经验系数，使得模型精度极大地依赖于这些经验系数的选择，对引射器的结构优化作用不大。此外，Nakagawa M等[11]通过实验发现，在CO2引射器喷嘴内部存在非平衡相变现象，均衡假设会产生较大误差。之后，Banasiak K等[10]建立了1D分布模型，并引入延迟均衡理论分析喷嘴内的非平衡相变现象。然而，该模型采用均匀成核理论计算非平衡相变过程的汽化指数，涉及多种物性参数，在CO2处于临界点附近时数值变化剧烈，当该模型应用于求解引射系数时，喷嘴临界流量的迭代会使得模型在某些工况下不收敛。

考虑CO2引射器内部的非平衡相变及传质传热过程，本文选用过热液体汽化的半经验计算式计算非平衡相变过程的汽化指数，建立了基于延迟均衡理论的1D分布模型，分析非平衡过程对引射器的影响，并采用该模型分析引射器混合室的结构对性能的影响。

1数学模型

根据引射器内不同的流动特点，对引射器分区域建模，如图1所示。模型中主动喷嘴(1、2)和引射喷嘴(3)均为单一流体；预混合室(4)、混合室(5)和扩压室(6)中为同轴混合流体区域。

1主动喷嘴渐缩段 2主动喷嘴渐扩段 3引射室 4预混合室 5混合室 6扩压室图1 跨临界CO2两相引射器计算示意图Fig. 1 Schematic of transcritical CO2 two-phase ejector

1.1 主动喷嘴和引射喷嘴

CO2在主动喷嘴和引射喷嘴中为单一流体流动。为了方便计算，假设：1) 喷嘴内为一维稳态流动；2) 液相和气相处于动态平衡；3) 忽略流体表面张力和热扩散的影响；4) 模型中不考虑湍流所产生的粘性耗散作用。从而喷嘴的控制方程为：

(1)

考虑到非平衡相变过程，CO2的平均物性(焓、密度)由方程(2)计算获得。

(2)

其中y为汽化指数[7]，定义为：

(3)

显然，当y恒等于1时，模型为均衡模型(HEM)。为保证方程组闭合，需添加汽化指数的微分方程。Banasiak K等[10]所采用的基于均匀成核理论的微分方程涉及物理变量多，而CO2在临界点附近物性变化剧烈，该方程会引起模型计算不收敛。因此，本文选用了文献[12]中推荐的过热液体汽化的半经验计算式：

(4)

式中:k为经验参数，通过与实验数据的拟合，本文中取值为2。此外，两相CO2声速由计算式(5)[13]进行计算。

(5)

1.2 预混合室

预混合室采用零维模型进行分析，假设：1) 流体稳态流动；2) 两股流体呈同轴流动，并最终达到相同压力；3) 两股流体之间没有质量传递。从而获得控制方程：

1) 质量守恒方程

Aλ,mnρλ,mnVλ,mn=Aλ,mixρλ,mixVλ,mix

(6)

2) 能量守恒方程

(7)

3) 等熵过程

sλ,mn=sλ,mix

(8)

4) 混合室入口的几何关系

(9)

式中：λ={α，β}，分别应用于计算主动流和引射流。该方程组采用牛顿迭代法进行求解。

1.3 混合室和扩压室

在1.1中的假设基础上添加以下假设对混合室和扩压室建模：1) 两种流体为同轴流动；2) 流体等压混合[8]；3) 流体通过冷凝、扩散进行相互作用；4) 模型考虑壁面摩擦和混合边界层粘性力所产生的动量及能量传递。由此获得控制方程组为：

1) 质量守恒方程

(10)

(11)

2) 动量守恒方程

1阀针 2主动流段 3主动流进口 4喷嘴距调节部分 5引射流进口 6混合段 7扩压段图2 可调引射器的结构尺寸Fig. 2 The structure and dimensions of the adjustable ejector

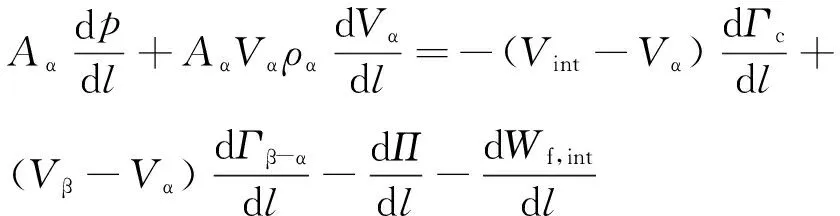
(12)

(13)

3) 能量守恒方程

(14)

(15)

4) 状态方程

(16)

式中：λ={α，β}。

5) 几何关系

(17)

模型中流体冷凝过程由计算式(18)给出。

(18)

(19)

壁面的对流换热量可由式(20)计算获得。

(20)

2 模型验证

带阀针的引射器可以通过调节阀针位置获得不同的喷嘴喉部面积，是一种结构简单的可调引射器[14-16]。图2所示为实验中所采用的可调引射器的具体结构及尺寸参数，喷嘴为渐缩结果，阀针的作用使得引射器喉部面积在0.16 mm2～2.54 mm2之间连续可调。阀针为锥形结构，以顶点为x=0 mm，阀针上不同位置x对应的阀针直径为：

(21)

从而不同的阀针位置可以获得不同的喷嘴结构和不同的喉部面积。实验中其他各设备的具体参数及测量系统参数见文献[17]所述。

为了验证所建立模型，本文针对喉部面积为0.3115 mm2(当量直径为0.63 mm)的引射器进行了一系列实验及模拟工作，比较结果如表1所示。可以看出，延迟均衡模型根据出口压力计算引射系数所产生的最大误差小于6%；根据引射流量模拟计算升压比所产生的最大误差小于±5.5%。因此，本文所建立的1D分布延迟均衡模型能够准确预测引射器的性能。

表1 模型计算结果与实验数据的比较

3 结果与讨论

为保证引射器的正常工作，CO2在主动喷嘴喉部应达到音速，此时，喷嘴的流量达到在对应工况下的最大值即临界流量。针对喉部当量直径为0.63 mm的引射器，图3比较了延迟均衡模型和均衡模型时主动流的临界流量，其中误差定义如式(22)。

(22)

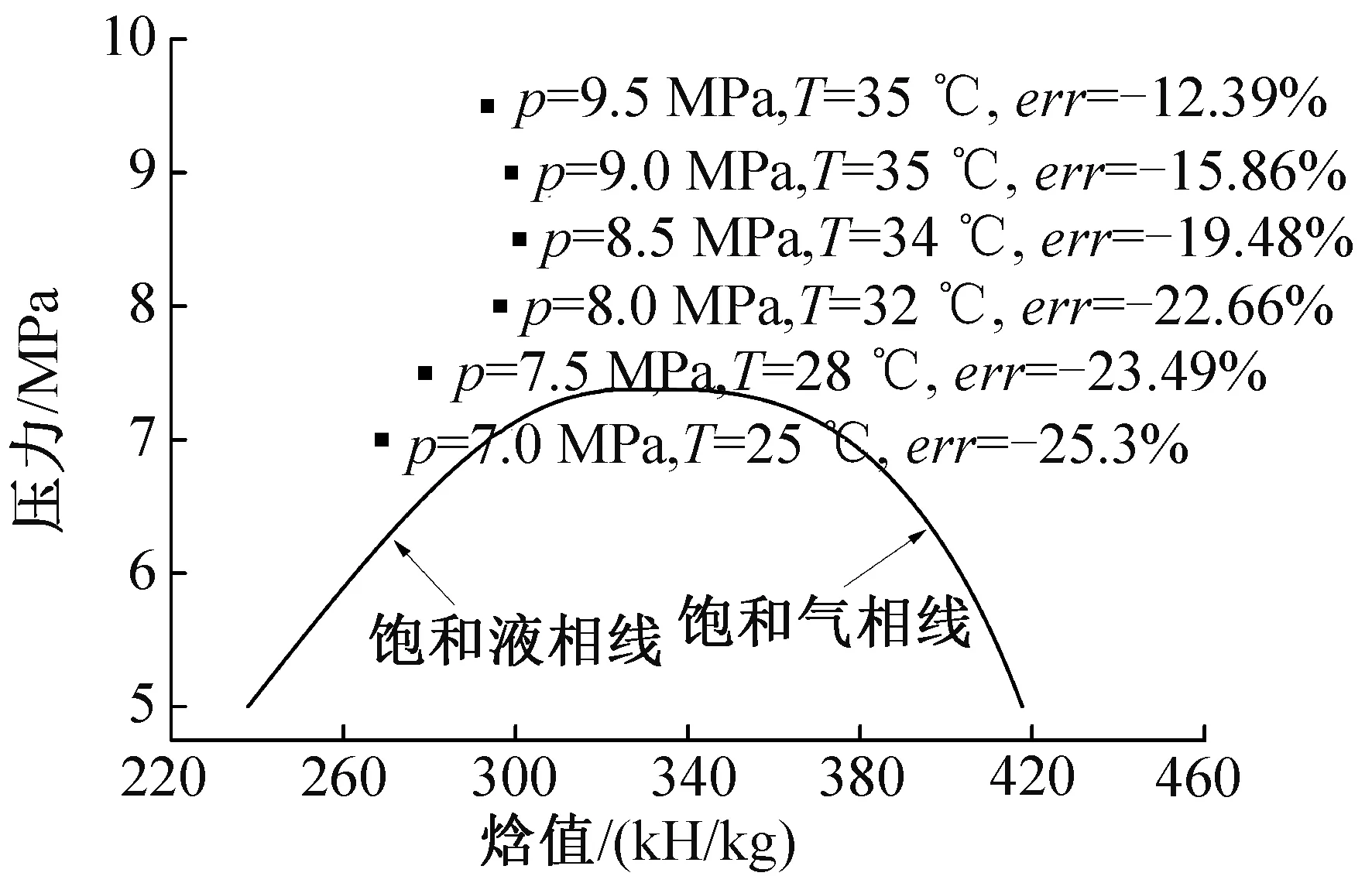
图3 不同工况下两种模型的比较Fig.3 Comparison of the two models with different operating conditions

本文选取如图3所示的6个主动流工况点，各工况下，流体在喷嘴中将经过过冷态以汽化成核的方式进入两相区，这些工况涵盖了CO2引射器运行时可能存在的大部分状态。比较结果显示，延迟均衡模型模拟出的主动流流量显著偏低，所选工况下比均衡模型的计算结果低12.39%～25.30%。

图4比较了主动流压力为9.5 MPa，温度为35 ℃时，分别采用延迟均衡模型和均衡模型计算所得的喷嘴内部的压力分布。由图可知，主动流进入两相区后，延迟均衡模型对应的非平衡过程使得流体膨胀缓慢，喷嘴出口压力高于均衡模型计算所得的压力值。

图4 不同模型时喷嘴内压力分布Fig.4 Pressure distribution in the nozzle for the two models

本文基于已建立的延迟均衡模型，进一步研究混合室直径和长度对引射系数和升压比的影响。默认工况为：主动流入口压力为9.8 MPa，温度35 ℃；引射流入口压力为3.8 MPa，温度为18 ℃。图5为当主动流压力分别为9.4 MPa、9.8 MPa和10.2 MPa时，引射系数和升压比随混合室直径变化的规律。由图可知随着混合室直径的增加，引射系数逐渐增大，而升压比逐渐减小。因此设计过程中，可以通过增加引射器混合室的直径提高引射器引射系数。然而当混合室直径继续增加，升压比将降低为1，引射器失去升压作用；而当混合室直径过小时，引射系数降低为0，引射器将失去引射作用。

图5 引射系数和升压比随着混合室直径的变化规律Fig.5 The variation of entrainment ratio and pressure lift with the mixing chamber diameter

图6 不同混合室长度下引射器内压力变化规律Fig.6 The pressure variation within the ejector at different mixing chamber lengths

进一步分析混合室长度对引射器性能的影响。图6显示了3种不同混合室长度的引射器中压力沿轴向距离的分布。结果显示混合室内，由于两种流体的混合，速度降低，动能转换为压力能，压力沿轴向增加；然而随着流体在混合室内的流动，混合损失及摩擦损失增加，流体压力逐渐降低。随着混合室长度的逐渐增加，混合室出口压力降低，而流体混合更加完全，扩压室中升压效果得到改善，引射器升压比增加(见图7)；当混合室长度过长时，混合室出口流体混合完全，而扩压室的升压无法弥补混合室内的损失，引射器的升压比逐渐降低(见图7)。此外，如图7所示，随着混合室长度的增加，升压比先显著增加然后缓慢减少，混合室内流体混合效果对引射器性能的改善较大，而损失对引射器性能降低较小。因此，混合室长度的设计不应过短，需保证两种流体的充分混合。

图7 升压比随着混合室长度的变化规律Fig.7 The variation of pressure lift with the diameter of the mixing lengths

4 结论

本文基于延迟均衡模型构建了CO2两相引射器1D分布模型，分析了非平衡相变现象对主动流的影响，并采用该模型分析了混合室结构对引射器性能的影响。所得结论如下：

1)本文所建延迟均衡模型能够很好地预测引射器的性能。与实验结果相比，模型计算引射系数误差小于6%，升压比误差小于5.5%。

2)与均衡模型相比，延迟均衡模型预测的主动流临界流量低12.39%～25.30%，同时喷嘴出口压力较高。

3)存在最佳的混合室直径使得引射系数和升压比都较高，而过小的混合室长度会显著降低引射器的升压效果。

本研究拓宽了引射器的理论研究，对引射器的设计优化具有重要的指导意义。

符号说明

下标

[1]Lee J S, Kim M S, Kim M S. Experimental study on the improvement of CO2air conditioning system performance using an ejector[J]. International Journal of Refrigeration, 2011, 34(7): 1614-1625.

[2]Sun F T, Ma Y T. Thermodynamic analysis of transcritical CO2refrigeration cycle with an ejector[J]. Applied Thermal Engineering, 2011, 31(6/7): 1184-1189．

[3]He Y, Deng J Q, Zhang Z X. Thermodynamic study on a new transcritical CO2ejector expansion refrigeration system with two-stage evaporation and vapor feedback[J]. HVAC&R Research, 2014, 20(6): 655-664．

[4]李倩, 郭宪民, 李卫国, 等. 跨临界CO2两相流引射制冷系统性能实验研究[J]. 制冷学报, 2012, 33(5): 15-19. (LI Qian, GUO Xianmin, LI Weiguo, et al. Experimental investigation on the performance of the transcritical CO2two-phase ejector refrigeration cycle[J]. Journal of Refrigeration, 2012, 33(5): 15-19.)

[5]徐肖肖, 陈光明, 唐黎明, 等. 带喷射器的跨临界CO2热泵热水器系统的实验研究[J]. 西安交通大学学报, 2009, 43(11): 51-55. (XU Xiaoxiao, CHEN Guangming, TANG Liming, et al. Experiment on performance of transcritical CO2heat pump water heater system with ejector[J]. Journal of Xi′an Jiaotong University, 2009, 43(11): 51-55.)

[6]任立乾, 郭宪民, 李添龙. 两段式喷嘴引射器及其引射制冷系统性能实验研究[J]. 制冷学报, 2014, 35(4): 21-24. (REN Liqian, GUO Xianmin, LI Tianlong. Experimental study on performance of dual-serial-throat nozzle ejector and two-phase ejector refrigeration cycle system[J]. Journal of Refrigeration, 2014, 35(4): 21-24.)

[7]Banasiak K, Hafner A, Andresen T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump[J]. International Journal of Refrigeration, 2012, 35(6):1617-1625.

[8]He S, Li Y, Wang R Z. Progress of mathematical modeling on ejectors[J]. Renewable and Sustainable Energy Reviews, 2009, 13(8): 1760-1780.

[9]Kolev N I. Entrainment in annular two-phase flow. Multiphase flow dynamics 2[M]. Springer, Berlin, 2007: 149-167.

[10] Banasiak K, Hanfer A. 1D computational model of a two-phase R744 ejector for expansion work recovery[J]. International Journal of Thermal Sciences, 2011, 50(11): 2235-2247.

[11] Nakagawa M, Berana M S, Kishine A. Supersonic two-phase flow of CO2through converging-diverging nozzles for the ejector refrigeration cycle[J]. International Journal of Refrigeration, 2009, 32(6): 1195-1202.

[13] Ameur K, Aidoun Z, Ouzzane M. Modeling and numerical approach for the design and operation of two-phase ejectors[J]. Applied Thermal Engineering in press, 2014.

[14] Liu F, Li Y, Groll E A. Performance enhancement of CO2air conditioner with a controllable ejector[J]. International Journal of Refrigeration, 2012, 35(6): 1604-1616．

[15] Lin C, Cai W, Li Y, et al. The characteristics of pressure recovery in an adjustable ejector multi-evaporator refrigeration system[J]. Energy, 2012, 46(1): 148-155.

[16] Varga S, Oliveira A C, Ma X, et al. Experimental and numerical analysis of a variable area ratio steam ejector[J]. International Journal of Refrigeration, 2011,34(7):1668-1675.

[17] 郑立星, 邓建强, 何阳. 两级蒸发对跨临界CO2引射制冷系统影响的实验研究[J]. 制冷学报, 2015, 36(4): 66-71. (ZHENG Lixing, DENG Jianqiang, HE Yang. Experimental investigation on the effect of the second stage evaporation on the transcritical CO2ejector expansion refrigeration system[J]. Journal of Refrigeration, 2015, 36(4): 66-71.)

About the corresponding author

Deng Jianqiang, male, professor, School of Chemical Engineering and Technology, Xi′an Jiaotong University, +86 29-82663413, E-mail:dengjq@mail.xjtu.edu.cn. Research fields: efficient chemical machineries and equipment.

A CO2Two-phase Ejector Model Based on Delayed Equilibrium Model

He Yang1Zhang Zaoxiao1,2Xue Changle2Zhang Yazhou2Deng Jianqiang2

(1. State Key Laboratory of Multiphase Flow in Power Engineering, Xi′an Jiaotong University, Xi′an， 710049, China; 2. School of Chemical Engineering and Technology, Xi′an Jiaotong University, Xi′an， 710049, China)

The ejector is key to the performance of the transcritical CO2ejector refrigeration system. Considering the complex processes, such as metastable phase change, supersonic flow, and choking phenomena et al., in the CO2two-phase ejector, a 1D distributed model was built in this paper and the delayed equilibrium theory was employed to analyze metastable phenomena in the motive nozzle. After the comparison with the relevant experiments data, the model was validated to be reliable to predict ejector performance. Compared with the homogeneous equilibrium model (HEM), the proposed model presented a 12.39%～25.30% lower critical mass flow rate. Meanwhile, the comparison results showed that the metastable phenomena would slow down the expansion process causing higher nozzle outlet pressure than that of the HEM simulation results. Moreover, the model is used to study the effect of the dimensions on the ejector performance and the results revealed that under a certain operating condition, an optimal mixing section diameter existed for both high entrainment ratio and pressure lift. Besides, a longer mixing section with a fixed mixing section diameter would increase the pressure lift ratio.

two-phase ejector; delayed equilibrium model; metastable phase change; CO2

0253- 4339(2016) 04- 0001- 06

10.3969/j.issn.0253- 4339.2016.04.001

国家自然科学基金 (51076120) 资助项目。(The project was supported by the National Natural Science Foundation of China (No. 51076120).)

2015年11月30日

TB61; TB657

A

简介

邓建强，男，教授，西安交通大学化学工程与技术学院，(029)82663413，E-mail：dengjq@mail.xjtu.edu.cn。研究方向：高效化工机械与设备。