非线性间隙气流激振力作用下汽轮机转子碰摩故障研究*

瓮　雷　杨自春　陈国兵　曹跃云　姜　尚

(1.海军工程大学舰船高温结构复合材料研究室　武汉　430033)(2.海军工程大学电子工程学院　武汉　430033)(3.92351部队　三亚　572016)



非线性间隙气流激振力作用下汽轮机转子碰摩故障研究*

瓮雷1杨自春1陈国兵1曹跃云2姜尚3

(1.海军工程大学舰船高温结构复合材料研究室武汉430033)(2.海军工程大学电子工程学院武汉430033)(3.92351部队三亚572016)

针对汽轮机机组存在的转静件碰摩问题，建立了汽轮机转子-轴承系统在非线性气流激振力作用下定子与转子碰摩模型及运动微分方程。采用数值方法研究了有无气流激振力对系统的非线性动力学行为的影响。结果表明：考虑气流激振力作用时，系统的混沌运动区域逐渐变小，频谱图出现幅值较大的谐波分量。并进一步以质量偏心为控制参数研究其对系统动力学特性的影响，得出一些有价值的结论。研究结果为汽轮机转子在非线性气流激振力作用下此类转子故障的动力学特性分析和故障诊断提供一定参考。

转子;非线性气流激振力;碰摩;混沌

Class NumberTH311；O322

1　引言

旋转机械是大型舰船、航空、化工、电力和机械等重要行业的关键设备，这些设备的安全、可靠、稳定运行关系到国防建设、国民经济和社会生活的各个方面[1]。转子作为舰船动力系统的核心部件，其与传动系统的振动噪声会严重影响到舰船尤其是潜艇等武器系统的隐蔽性能。造成系统异常振动或振动过大包括多个方面的原因，转静件的碰摩是其中重要原因之一。

近年来，国内外众多学者对碰摩转子系统的非线性动力学行为进行了研究。李振平等[2]应用多初始点分岔分析方法对碰摩转子系统的非线性动力学行为作了全面的分析。Shen X Y等[3～4]分析研究了质量偏心对碰摩故障转子系统非线性动力学行为的影响。张雷克等[5]针对UMP引起的转子与定子碰摩问题，研究了系统随励磁电流、质量偏心和定子径向刚度参数变化的非线性动力学行为；陶海亮等[6]建立了非线性油膜力作用下，具有弹性静子的转子-轴承系统碰摩故障模型，对比研究了有无碰摩故障下系统的动力学特性。

汽轮机机组转子系统除了受到重力、偏心力、非线性油膜力等外力作用外，还承受着一个作用在转子轴心上的非线性气流激振力[7～8]。文献[9～10]研究非线性气流激振力使得转子系统偏于失稳。吴敬东，张旭东等[11]研究了刚性Jeffcott转子系统在汽轮机非线性间隙气流激振力和密封流体激振力共同作用下的非线性振动特性。瓮雷等[12～13]研究分析了在气流激振力作用下的含有裂纹故障转子系统非线性动力学行为。随着旋转机械效率的提高，当激振力增大到一定程度，势必造成定子与转子之间碰摩故障的反生，甚至造成巨大的人员和经济损失。

这些文献研究了汽轮机非线性气流激振力或碰摩故障对转子系统非线性动力学特性的影响，得出了一些非常有价值的结论。但对非线性间隙气流激振力转子系统的研究主要是基于刚性支承的Jeffcott转子模型，忽略了陀螺效应和支承弹性，且对于碰摩和汽轮机非线性间隙气流激振力耦合故障下的转子非线性动力学研究还比较少。本文针对汽轮机非线性气流激振力引起的转静件碰摩问题，建立了汽轮机转子-轴承系统模型，推导其运动微分方程。比较分析了是否考虑汽轮机非线性气流激振力对系统动力学特性的影响，以及转子质量偏心作为控制参数，采用数值方法研究了不同参数变化时系统的非线性动力学行为，为汽轮机转子在非线性气流激振力作用下转静件碰摩故障的动力学特性分析和故障诊断提供一定参考。

2　转子碰摩故障动力学模型

本文以对称油膜支承的含碰摩故障转子-轴承系统作为研究对象，忽略扭转振动和陀螺力矩，只考虑转子的横向振动，如图1所示，研究在汽轮机非线性间隙气流激振力作用下的非线性动态响应。其中O1、O2分别为轴承内瓦和转子几何中心，O3为转子质心；转子两端由半径为R、长为L的滑动轴承支承，m1、c1和m2、c2分别为转子在轴承处和圆盘处的等效集中质量和结构阻尼，e为圆盘的质量偏心，Fx、Fy为非线性油膜力，c为平均油膜厚度，μ为润滑油粘度；δ为Sommerfeld修正系数。

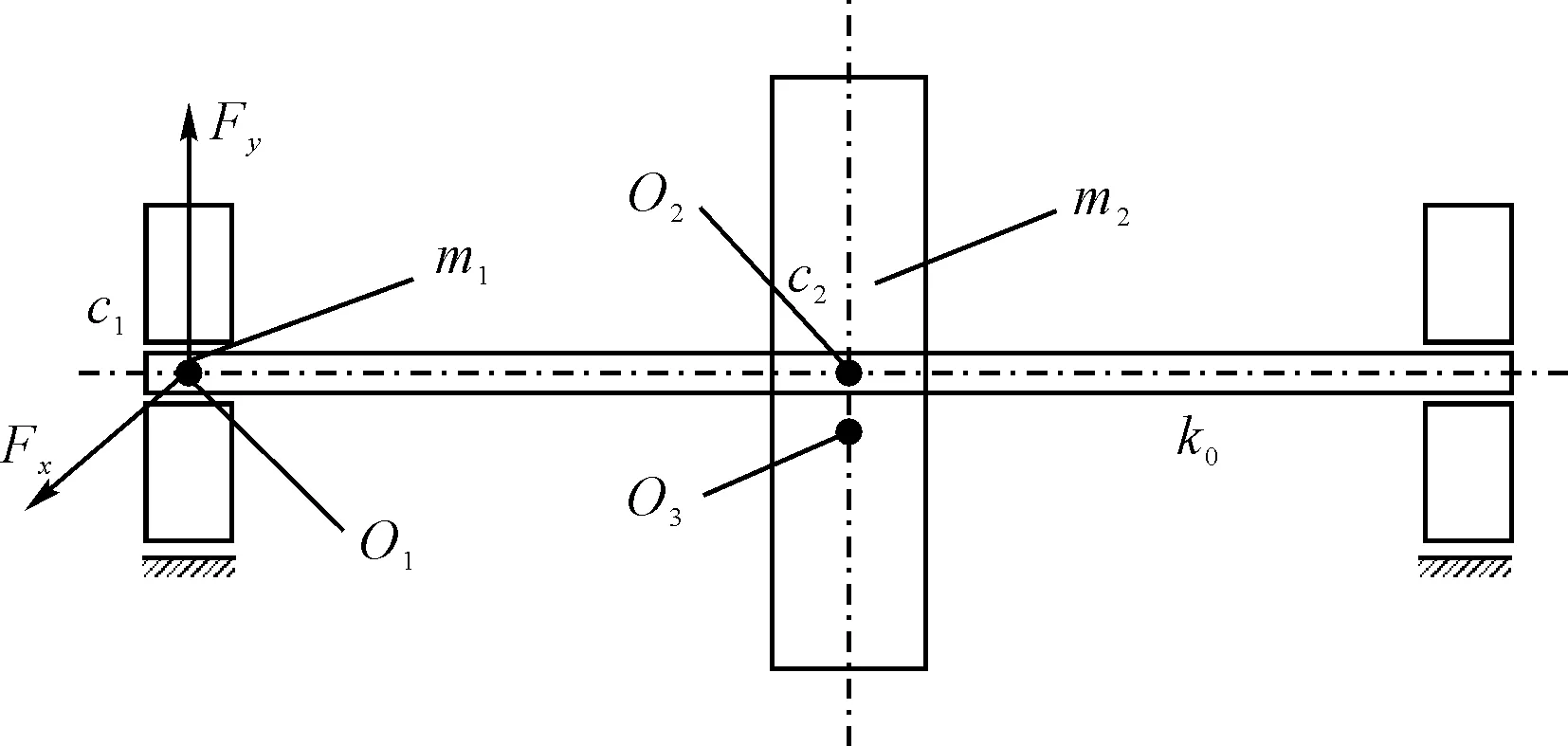
图1　油膜支承转子系统示意图

2.1汽轮机气流激振力模型

本文以某型汽轮机转子为研究对象，系统结构及受力简图如图2所示。fax、fay为气流激振力Fa在x、y方向的分力。非线性气流激振力采用文献[13]中无量纲激振力模型：

Fa=A1·δ·E+A3·δ3·E3

式中：

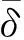
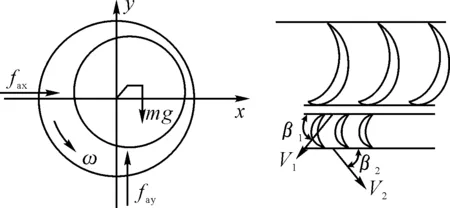
图2　系统受力图及气流流动示意图

2.2汽轮机转子碰摩力模型

当转子系统含有碰摩故障时，系统是分段线性刚度的非线性振动系统。为了研究方便，不考虑碰摩转子在运行过程中由于摩擦产生的热效应，且视转子与定子之间的碰撞为弹性碰撞。转子与定子局部碰摩模型如图3所示。设系统在静止时转子与定子之间的间隙为δ0，当发生碰摩时，其法向碰摩力与切向碰摩力可表示为

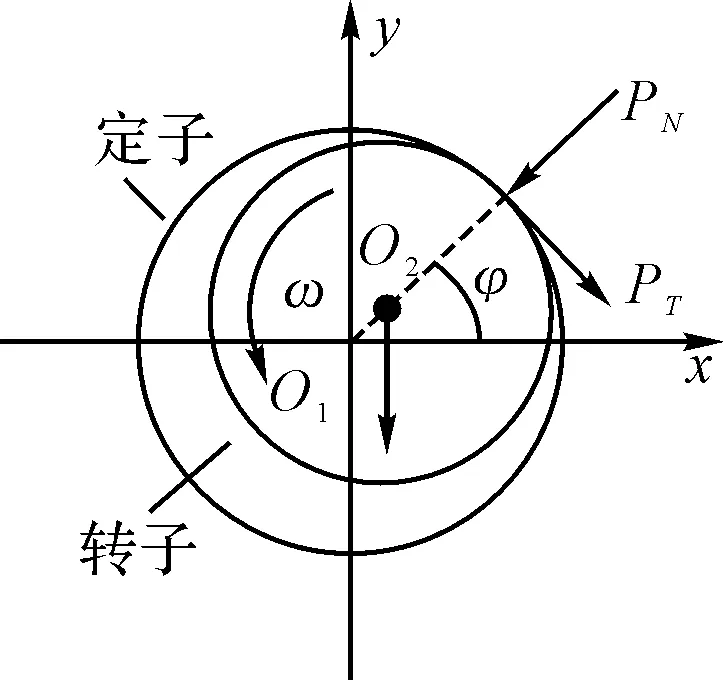
图3　转子碰摩力模型

在x-y坐标系碰摩力可分解的x、y方向的分量为

由以上分析可得转定间碰摩力最终可表示为

2.3非线性气流激振力作用下系统的运动微分方程

设转子左端轴承处的径向位移为x1、y1；转盘处的径向位移为x2、y2。则气流激振力作用下系统的运动微分方程为

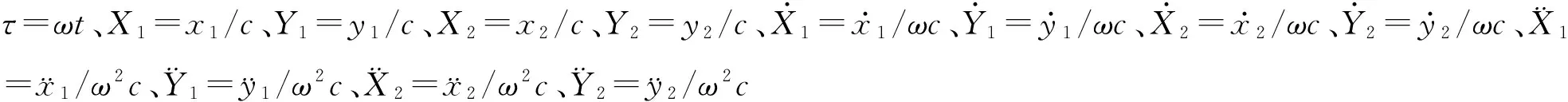
3　仿真结果及分析研究

为了了解系统的动力学特性，需研究参数发生变化时系统的各种运动现象。本文采用龙格库塔方法求解非线性振动微分方程。通过数值仿真获得系统在不同参数变化下的振动响应，进而给出在汽轮机非线性间隙气流激振力作用下含裂纹转子碰摩耦合故障时的振动分岔图、轴心轨迹图、和Poincare截面图。设定转子动力学模型中的参数。

本文转子轴承系统的主要参数为：m1=4.0kg，m2=32.1kg，R=25mm，L=12mm，μ=0.018pa·s，c1=1050N·s/m、c2=2100N·s/m、k=2.5×107N/m，kc=3.6×107N/m，b=0.11mm，f=0.1，δ0=0.2mm，e=0.05mm。气流激振力的参数选取如下：ρ0=11.8kg/m3，RT=0.5m，RB=0.37m，β1=35°，β2=40°，ζ=0.83，δ=1.2×10-3m，V=200m/s。系统一阶临界转速为ω0=882.5rad/s。

3.1非线性气流激振力对转子振动特性的影响

图4(a)和图4(b)为考虑和不考虑非线性间隙气流激振力作用时碰摩转子系统随转速变化的响应分岔图。对比研究图4(a)和图4(b)可以看出：随着转速的增大，系统均是先后经历周期1运动、周期2运动、周期4运动、复杂运动、周期4运动、高速域的复杂运动。但是，在考虑非线性间隙气流激振力时，系统在临界转速附近出现的混沌区域明显减少，且运动变得复杂化。图5为考虑和不考虑气流激振力作用时截取的局部分岔图。由图可以明显看出，考虑气流激振力时系统的混沌运动区域变小，且在系统响应为混沌的分岔图演变为四条被压扁的自相似轨迹，在Poincare截面图上表现为四个独立的岛状，且频谱图包含除了工频和1/2分频外多了1/4和3/4分频，如图6(a)和6(b)所示。此外，还出现短暂的周期12和周期8运动，如图6(c)和6(d)所示，在Poincare截面上表现为12个和8个孤立的点。

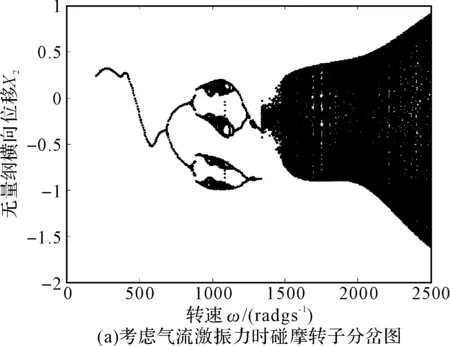
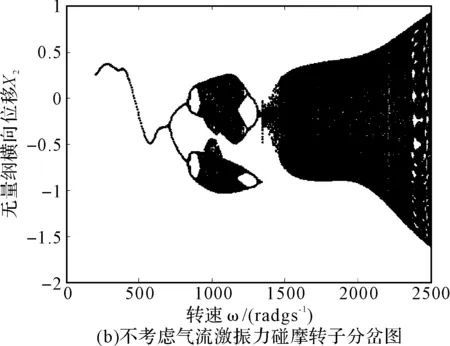
图4　碰摩转子系统随转速变化的响应分岔图

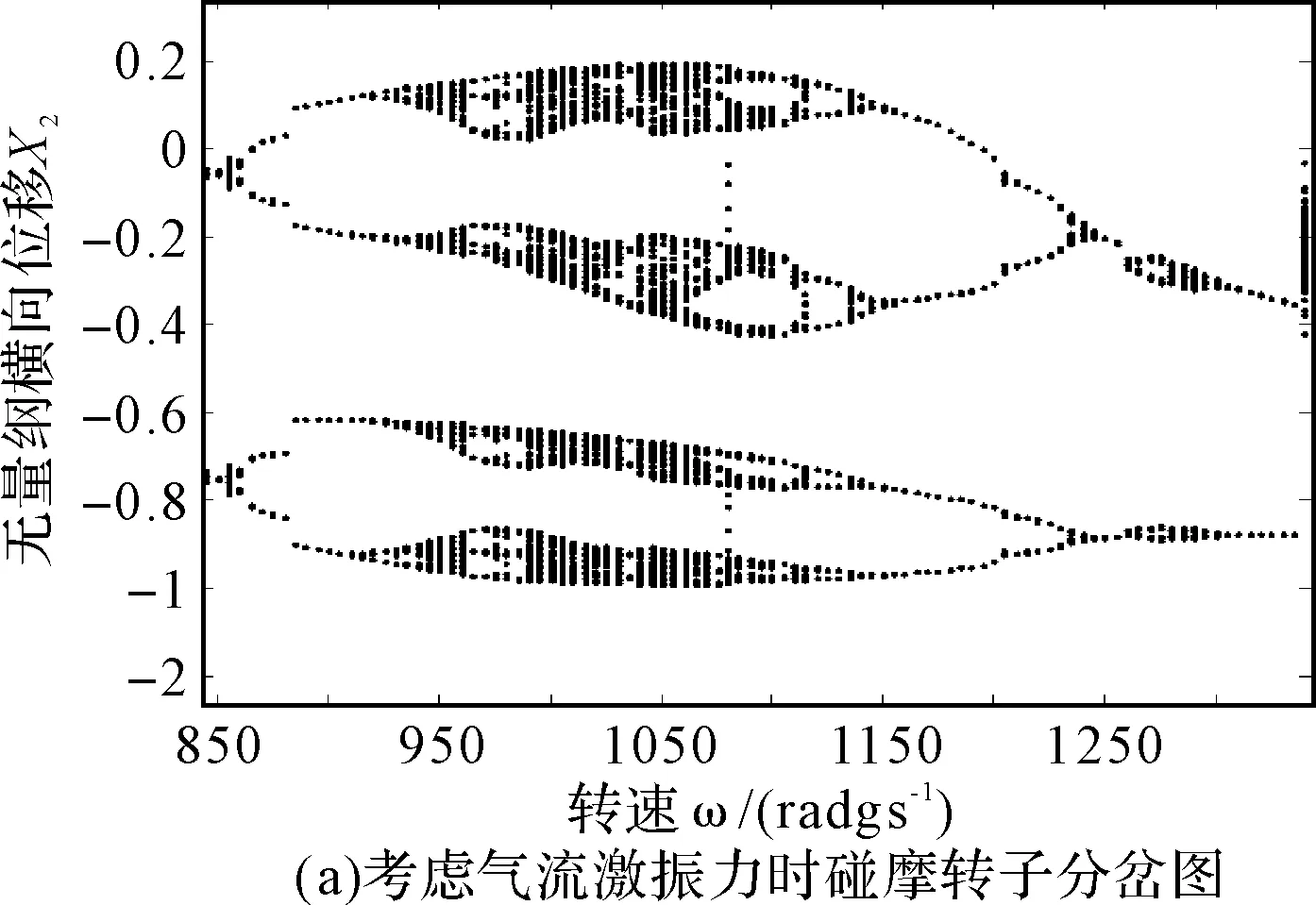
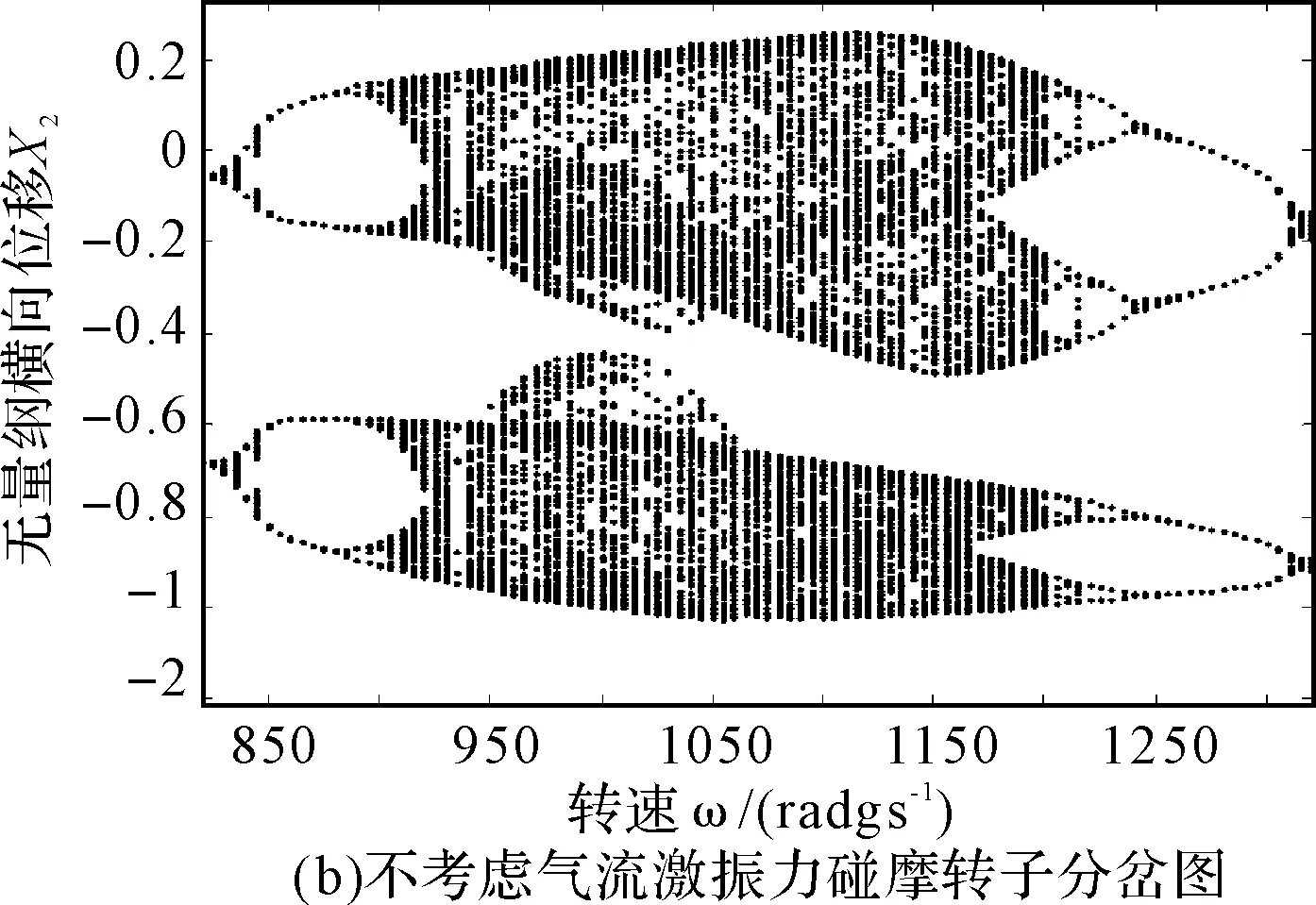
图5　考虑和不考虑气流激振力时转子系统的局部分岔图

综上可知，当考虑气流激振力的作用时，碰摩转子系统的动力学特性变得复杂化，这主要是由于气流激振力与碰摩力以及非线性油膜力相互之间耦合作用的结果。因此，很有必要进一步研究在气流激振力作用下，碰摩故障转子轴承系统的动力学特性，进一步了解这种故障状态下转子的振动特性。

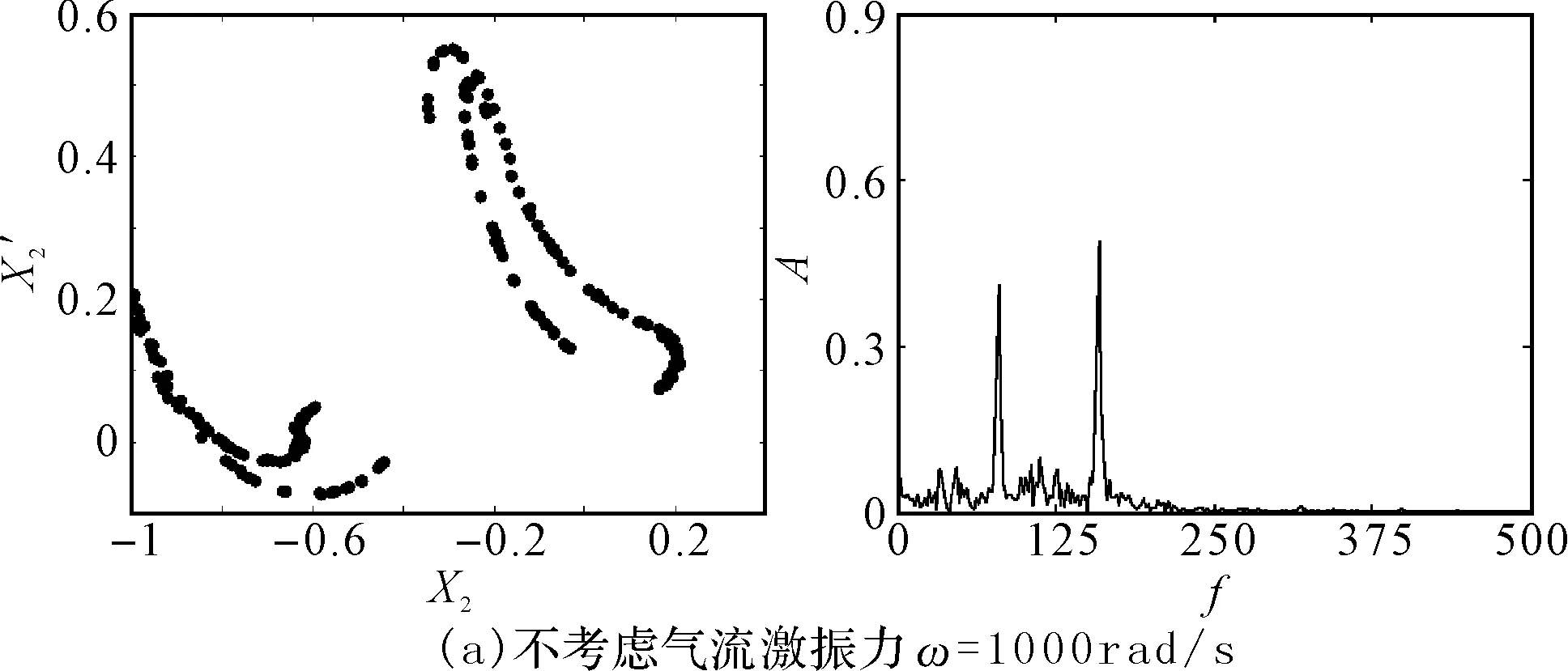
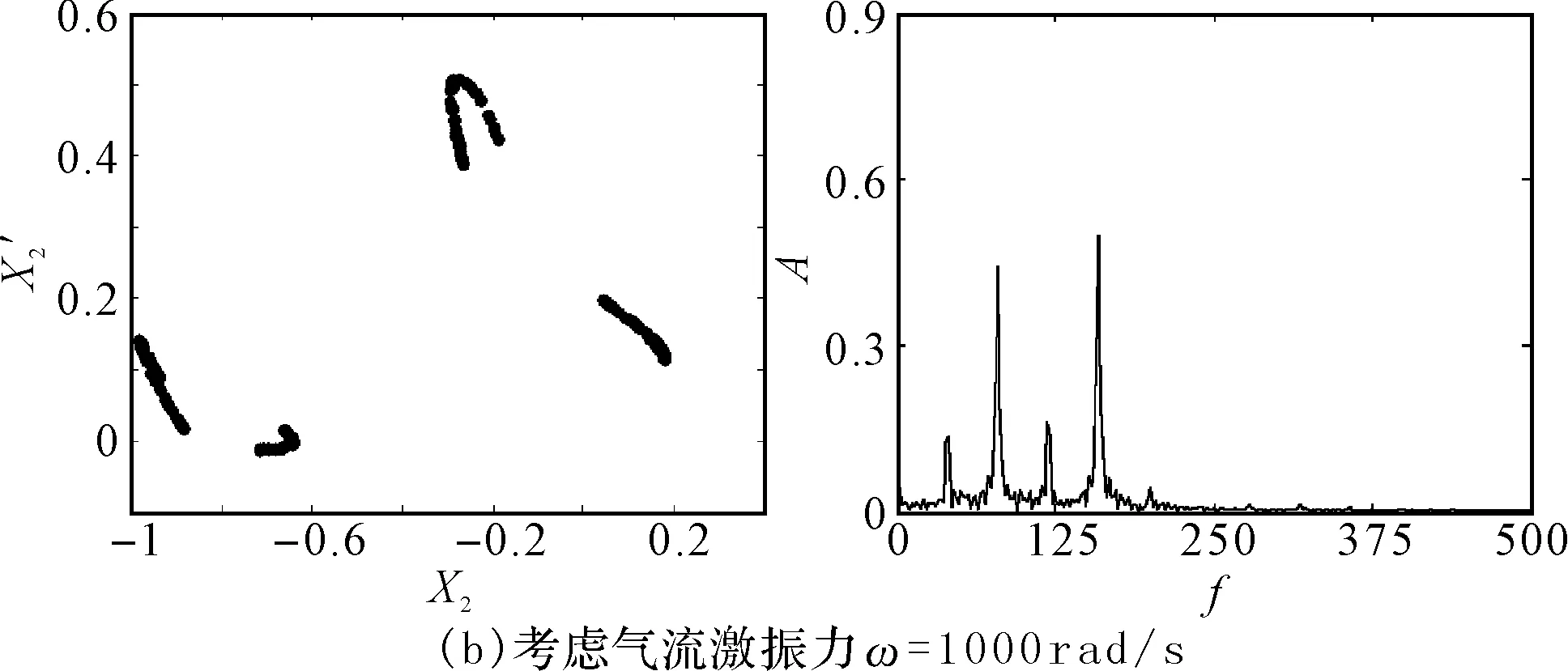
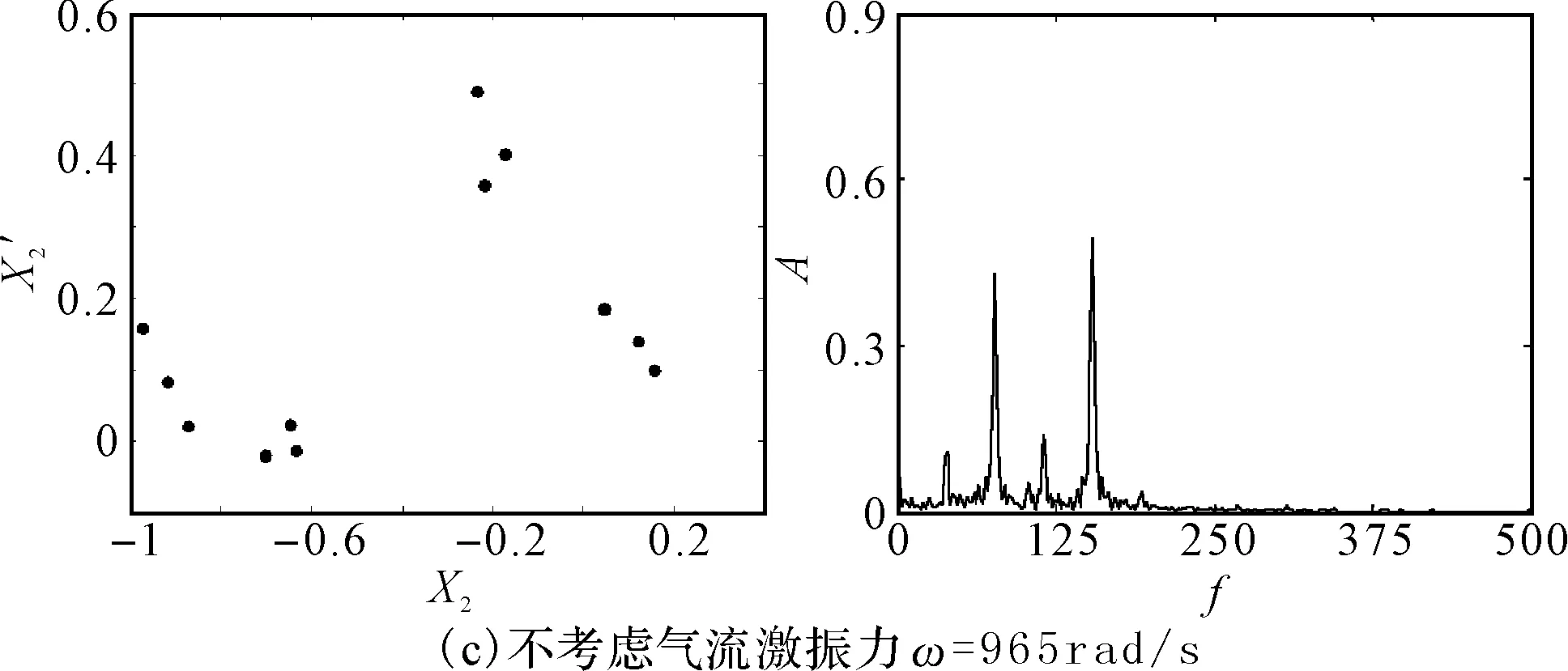
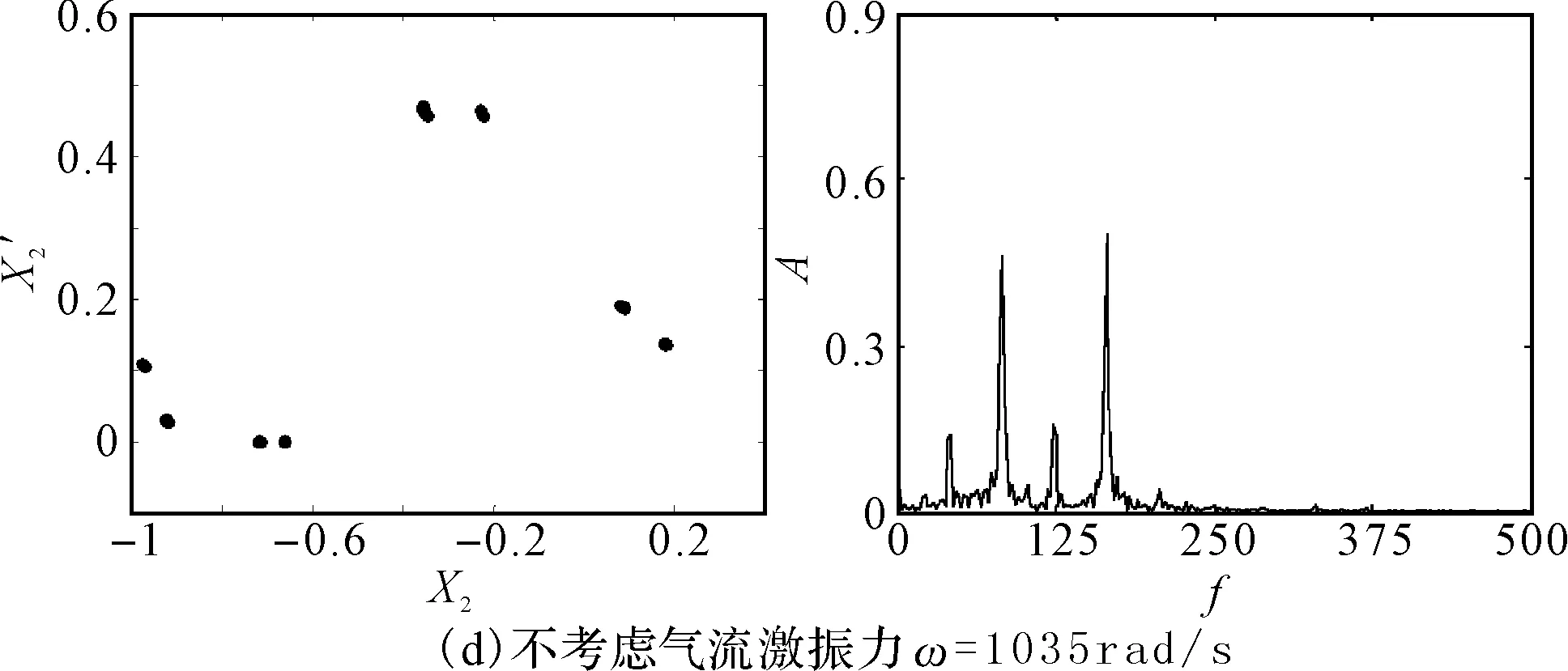
图6　系统在不同情况下的Poincare截面图和频谱图

3.2质量偏心对碰摩转子系统振动特性的影响

转子系统在投入使用前需要预先进行动平衡测试和校对，但由于加工、装配、腐蚀等因素，转子系统仍旧可能产生偏心，进而引起转子系统的振动以至于产生碰摩，对机组的正常运行会造成很大的影响。转子偏心量作为直接关系到机组运行稳定的一个非常重要的参数，因此，研究其变化对系统动力学行为的影响是十分有意义的。

图4(a)和图4(b)分别对应于不考虑和考虑汽轮机非线性间隙气流激振力作用时，碰摩转子系统随质量偏心e变化的分岔图。从图4(a)可以看出，不考虑汽轮机非线性间隙气流激振力时，系统先后经历周期1运动、周期2运动、周期4运动、周期8运动、混沌等运动形式。如图4(b)为考虑非线性间隙气流激振力时，系统的分岔特性与图4(a)相似，但在某些区域出现了较大的变化。当考虑气流激振力时，随着转子偏心量的增大，由于非线性间隙气流激振力的作用，碰摩转子系统的周期性分岔运动演变为拟周期运动，如图5(a)所示，轴心轨迹为多条复杂的环形，在庞加莱截面图上呈现为一个封闭的曲线。随着偏心量的进一步增加，非线性间隙气流激振力使得系统的四倍分岔运动短暂的演变为倍周期分岔又回到四倍周期分岔。随着偏心量的进一步增大，气流激振力的作用对系统的影响加强，如图5(b)和图5(c)所示系统的部分混沌运动演变为四倍周期分岔。之后系统又进入混沌运动并突变为响应幅值较大的周期性稳态运动，这主要是由于质量偏心对系统的动力学特性的影响更加显著起主导作用。

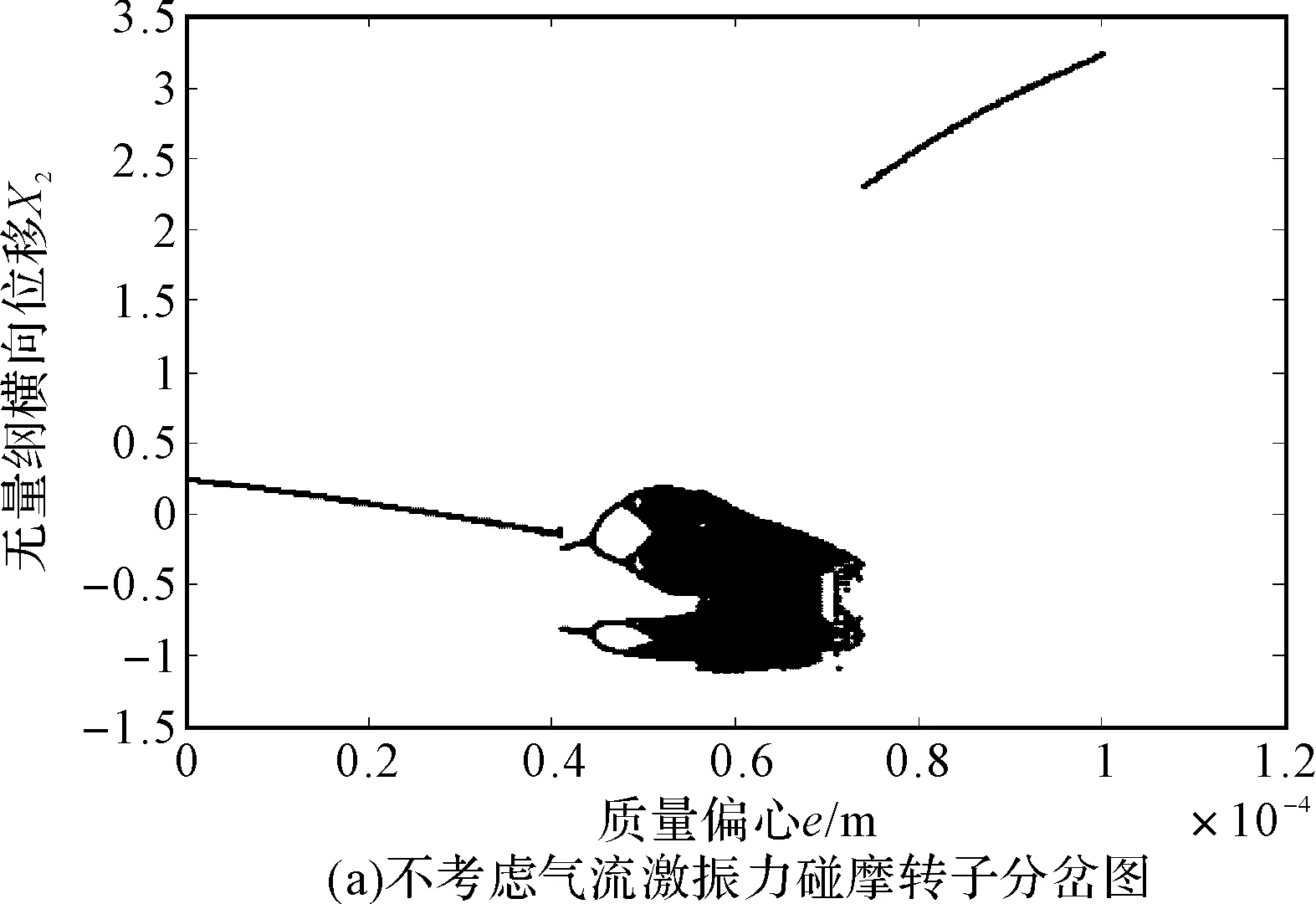
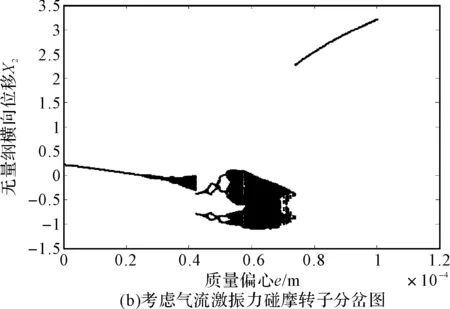
图7　碰摩转子系统随质量偏心变化的分岔图

由上述分析说明考虑非线性间隙气流激振力作用后，碰摩转子系统的动力学特性发生了明显的变化，主要是由于非线性间隙气流激振力的存在降低了系统的固有频率，进一步增强了质量偏心对碰摩转子系统运动特性的影响。

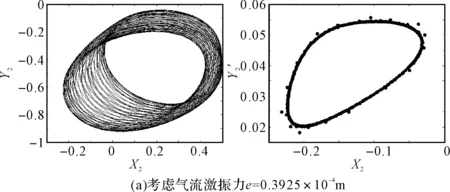
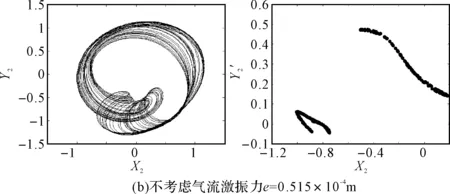
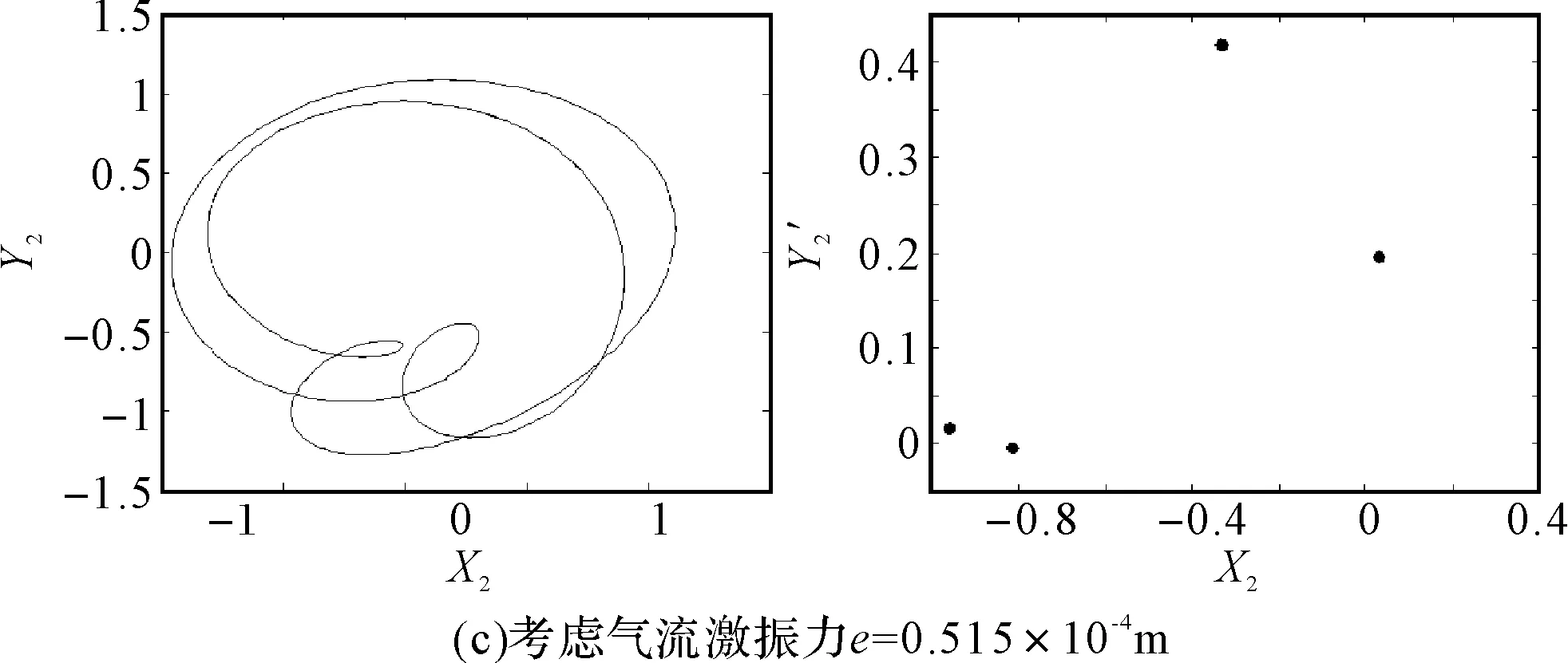
图8　不同偏心量下转子的轴心轨迹和Poincare截面图

4　结语

1)在考虑非线性气流激振力时，由于气流激振力与碰摩力以及非线性油膜力相互之间耦合作用，系统在临界转速附近出现的混沌区域明显减少，且运动变得复杂化,频谱图包含除了工频和1/2分频外多了1/4和3/4分频。此外，还出现短暂的周期12和周期8运动。

2)在气流激振力作用下，当质量偏心增大到一定程度时，由于非线性间隙气流激振力的存在降低了系统的固有频率，进一步增强了质量偏心对碰摩转子系统运动特性的影响，质量偏心对碰摩转子系统的非线性动力学特性的影响更加显著。

[1]李明,李自刚.完整约束下转子-轴承系统非线性振动[M].北京：科学出版社，2014.

[2]李振平，张金换，金志浩，等.碰摩转子-轴承系统非线性动力学行为研究[J].航空动力学学报，2004，19(2)：179-183.

[3]Shen X Y,Jia J H,Zhao M.Effect of parameters on the rubbing condition of an unbalanced rotor system with initial permanent deflection[J].Archive of Applied Mechanics,2007,77(12):883-892.

[4]Shen X Y,Jia J H,Zhao M.Numerical analysis of a rub-impact rotor-bearing system with mass unbalance[J].Journal of Vibration and Contoal,2007,13(12):1819-1834.

[5]张雷克，马震岳.不平衡磁拉力作用下水轮发电机组转子系统碰摩动力学分析[J].振动与冲击，2013，32(8)：48-67.

[6]陶海亮，左志涛，高庆，等.基于时频分析的裂纹转子碰摩故障特征研究[J].推进技术，2013，34(4)：520-528.

[7]柴山，张耀明，赵又群，等.汽轮机非线性间隙气流激振力分析(Ⅰ)——相对进气速度沿叶高不变[J].非线性动力学学报，2000，7(1)：25-32.

[8]Chai Shan,Zhang Yaoming,Zhao Youqun,et al.An analysis on the non-linear air exciting-vibration force caused by clearance[J].Journal of Nonlinear Dynamic in Science and Technology,2000,7(1):25-32.

[9]H.S.Kim.Stability analysis of a turbine rotor system with Alford forces[J].Journal of Sound and Vibration,2002,258(4):777-790.

[10]辛晓辉，曹树谦，丁千.汽轮机转子在气流力和油膜力作用下的非线性动力学特性[J].非线性动力学学报，2005，12：45-52.

[11]吴敬东，张旭东，鄢利群，等.气流激振力作用下转子的非线性特性研究[J].沈阳化工大学学报，2011，25(4)：343-348.

[12]瓮雷，杨自春，曹跃云.汽轮机非线性间隙气流激振力作用下转子系统的分岔研究[J].海军工程大学学报，2015，27(5)：52-57.

[13]瓮雷，杨自春，曹跃云.汽轮机非线性间隙气流激振力作用下含裂纹转子的振动特性研究[J].振动与冲击,2016,35(5):89-95.

Dynamic Analysis for Rotor System with Rub-impact of A Steam Turbine Under the Air-exciting Force

WENG Lei1YANG Zichun1CHEN Guobing1CAO Yueyun2JIANG Shang3

(1.Institute of High Temperature Structural Composite Materials for Naval Ship，Naval University of Engineering,Wuhan430033)(2.Electronic Engineering College,Naval University of Engineering,Wuhan430033)(3.No.92351 Troops of PLA,Sanya572016)

The dynamic model of a rub-impact rotor bearing system with under the air-exciting force of steam turbine was established and the corresponding equations motion were derived.Nonlinear method was adopted to investigate the nonlinear dynamic response of the system.The dynamic characteristics of the system with or without the air-exciting force were compared and discussed.Simulation results showed that the chaotic motion region of the system decreases when considering the air-exciting force of the steam turbine.The spectrum was composed of continuous and broad band frequencies.The rotor mass eccentricity was also studied and obtained some useful conclusions.It was indicated that this study may contribute to further understanding of failure mechanism of such a rotor-bearing system.

rotor,air-exciting force of steam turbine,rub-impact,chaos

2016年3月22日,

2016年4月28日

国家自然科学基金项目(编号：51509254)；武器装备预研基金项目(编号：9140A27030514JB11449)；海军工程大学自然科学基金项目(编号：HGDQNJJ13013)；国家部委基金项目(编号：010502010261002)资助。

瓮雷，男，博士研究生，研究方向：舰船动力及热力系统的科学管理。

TH311；O322DOI：10.3969/j.issn.1672-9730.2016.09.023