轻型夯法工艺对桥基变形的影响及离散元分析*

杨丰春，马宗源，党发宁

(西安理工大学 土木建筑工程学院，西安 710048)



轻型夯法工艺对桥基变形的影响及离散元分析*

杨丰春，马宗源，党发宁

(西安理工大学 土木建筑工程学院，西安 710048)

旨在分析台背回填施工中轻型夯法工艺对桥基水平位移变形(简称水平位移)的影响.利用颗粒离散元方法分析了桥基在不同碎石土接触刚度、夯击点距结构边缘水平间距(简称夯击间距)、夯击次数、夯锤落高与重量及不同夯锤与路基接触面形状(简称接触面形状)下的水平位移规律.与现场实测值及静止土压力作用下的理论水平位移值进行了比较.结果表明：夯击间距与接触面形状较其他参数对桥基水平位移的影响程度更大；相同夯击能级下，“轻锤高落”比“重锤低落”引起桥基产生的水平位移量值小；有、无夯击垫板情况下桥基产生的最大水平位移为仅在静止土压力作用下的2.65 倍、3.56 倍.

离散元；桥基变形；轻型夯法；夯击能级

tamping energy level

快速液压轻型动力夯实法(简称轻型夯法)作为解决公路中“桥头跳车”等问题的有效方法，在公路桥台背侧回填(简称台背回填)加固施工中得到广泛应用.但此法同时又不可避免的会对桥台结构产生不利影响，如局部开裂甚至整体倾覆.作为一种较新的施工工艺，轻型夯法针对不同工况的施工参数有待论证.如在固定锤重及落高情况下为控制对临近结构的不利影响，如何选取施工的最小安全距离[1-4].当前研究中常以速度、加速度[5-6]及应力等量值作为施工对周围环境结构物产生影响的研究对象，但得到的结果有限且突变性较大，同时实验造价高，较难还原对结构的真实影响，尤其是结构内部应力最大值及位置等的判断.位移变形量作为衡量夯击对结构影响程度最直观的指标，使用位移检测计和应变片测量能够较可靠的记录结构的变形量值.

颗粒流离散元方法适于模拟散体颗粒组成的非连续性、无粘性和大变形等性质材料(如公路路基碎石土)以及具有脆性破坏的特性的材料(如桥基混凝土).文献[7]利用颗粒离散元法研究孔隙率受不同夯击参数的影响，模拟出了碎石土在动力夯实过程中的大变形、大孔隙及非线性的动应力应变关系等特性.针对挡土墙背侧冲击作用对结构物的影响，文献[8-9]结合Boussinesq解,推导并给出了冲击荷载作用时挡土墙上所受土压力的实用计算公式，采用有限元法研究了冲击荷载作用下对结构位移变形的影响，结合实际论证其正确性.

本文以轻型夯法工艺为背景并以桥基不同位置处的水平位移作为变形研究对象，利用PFC2D离散元程序模拟动力夯实过程，研究各因素对桥基水平位移规律的影响大小，论证此方法针对动力夯击过程中碎石土的特性、碎石土与结构相互作用特性模拟的适用性，为桥基工程提供参考.

1　颗粒流离散元理论及模型建立

1.1颗粒流离散元理论

颗粒流离散元方法(Particle Flow Code，PFC)是研究圆形颗粒体运动及其相互作用的方法，最早由Cundall和Strack[10]提出其计算基本框架，主要适用于分析离散性较强的不连续介质如破碎岩石、砂土及混凝土等的运动形态及力学行为.当前颗粒离散元法中粒子之间接触的物理状态[11]包括多种，其中颗粒接触模型反映块体或散体颗粒在接触点或接触面所作用的挤压和摩擦作用，同时其可模拟大变形、非线形等特性.文中考虑球体间的摩擦及阻尼的线弹性的接触模型，采用程序PFC2D来模拟砂、卵砾石及碎石土的力学行为.线弹性接触关系的表达式为

ΔFn=knΔUn,ΔFs=ksΔUs,ΔFs=μΔFn

(1)

式中：kn,ks分别为颗粒间法向及切向接触刚度；μ为摩擦系数；ΔUn,ΔUs分别为颗粒间法向、切向相对位移；ΔFn,ΔFs分别为颗粒间法向、切向作用力.其中考虑到夯击过程中的循环荷载产生的动力滞回效应，加卸载刚度相应取得不同的分段线性的回路曲线形式.

在颗粒离散元法中，颗粒静力平衡遭到破坏时，粒子就会发生运动(平动及转动).即每一个颗粒单元在任意时刻都满足运动方程(即牛顿第二定律)，这也限制程序PFC2D研究对象的自由度只能与位移和力有关.颗粒的坐标根据颗粒平动与转动方程解得速度并随计算步的改变实时更新.由各球的新位置坐标可判定相邻的颗粒是否接触或者原接触点是否脱离，若相互接触的球会改变球间重叠量，再由不同接触模型公式(如线弹性接触模型)更新接触力，如此反复迭代运算直到颗粒平衡力满足要求，计算循环如图1所示.

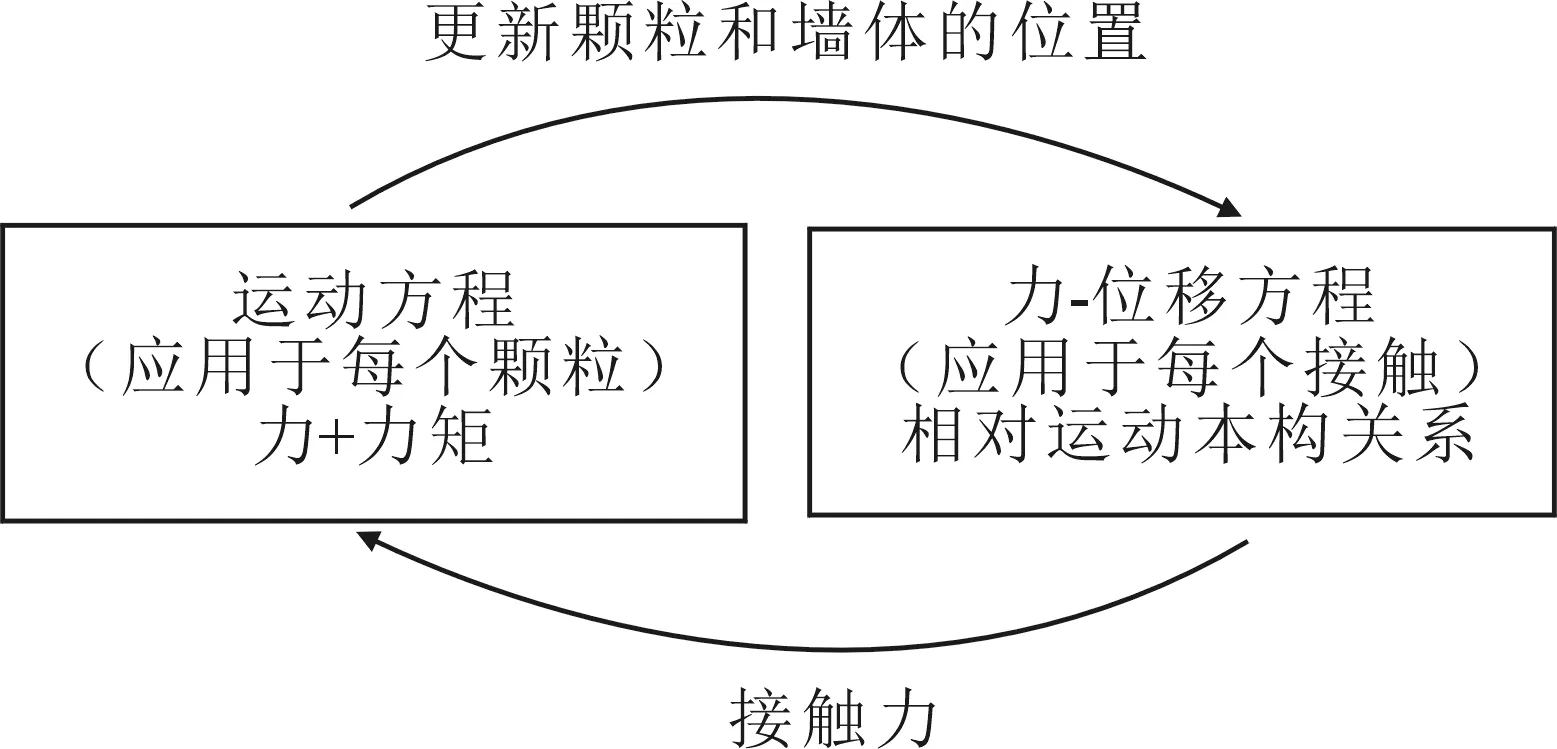
图1　颗粒流离散元法中的计算循环

1.2现场位移测量与模型建立

以某在建高速公路桥基结构背侧回填工程的动力夯实为背景.桥基总高10 m，桥基宽1 m，长21.5 m，距桥基底部3 m以上部分仅在桥基一侧回填碎石土，回填高度为5 m，并在此侧距离桥基边缘一定夯击间距进行夯击，具体工程尺寸如图2所示,R为夯锤半径.桥基采用现浇钢筋混凝土结构，混凝土材料为C30级.路基回填材料为就近开山破碎的筛分碎石与土混合的碎石土，碎石土筛分试验结果：试样中石料最大粒径小于200 mm，碎石含量大于60%.标准击实试验结果：试样中粒径小于38 mm的最大干密度为2.44 g·cm-3.

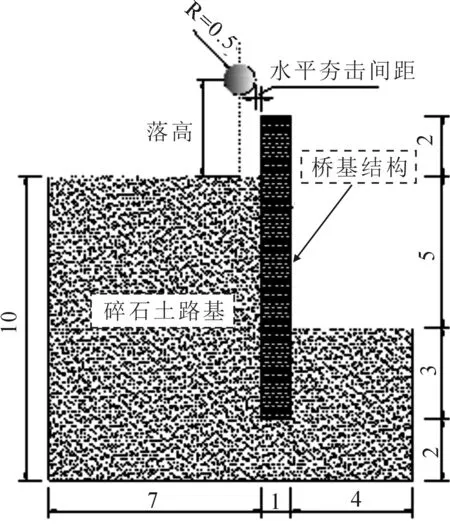
图2　夯实模型尺寸图(m)

动力夯击设备采用HHT-3型快速液压夯实机，设备具体参数：夯实机的总质量为20.0 t，液压系统工作压力为16 MPa；夯锤是工作装置,锤重G=3.0 t并与油缸的活塞杆相连，在重力与液压蓄能器的作用下加速下落冲击路基，快速的上下往复运动实现对路基单点或多点的连续夯击；夯锤最大行程即落高h=1.2 m，根据不同的作业要求,可

选择不同的下落高度.

1) 现场水平位移变形量

试验用到的设备为位移传感器和数据采集仪，当快速液压夯实机工作时，结构物受到冲击作用下发生位移变形，从而使位移传感器产生的电信号传输到数据采集仪，并在显示窗口显示数据.为了保护测试装置避免施工过程中破坏，位移传感器、数据采集仪等装置均布设在桥基未填土一侧(即右侧)的中轴线从下向上纵向间隔1.0 m布置.离散元模型中选取桥基上不同深度处的颗粒单元作为“位移观测点”并记录其夯击过程中的水平位移变化量.

2) 模型建立

二维颗粒流离散元计算程序PFC2D基于微观颗粒的接触本构关系反映宏观材料的力学行为.其中离散元模型以刚性“墙”为边界，考虑了碎石路基土的离散特性，在规定区域内按高斯分布以一定的粒径范围生成路基碎石土颗粒并在重力下固结；在规定位置处按规则紧密交错方式生成桥基结构物和夯板.

由于现实工程中桥基深度较大，一般不会发生沉降或者水平移动等问题，故约束桥基模型底部位移但不限制其转动，模拟其大变形及倾覆的可能.根据现场材料，模型材料参数见表1，建立离散元模型如图3所示.

表1　材料参数Tab.1　The material parameter

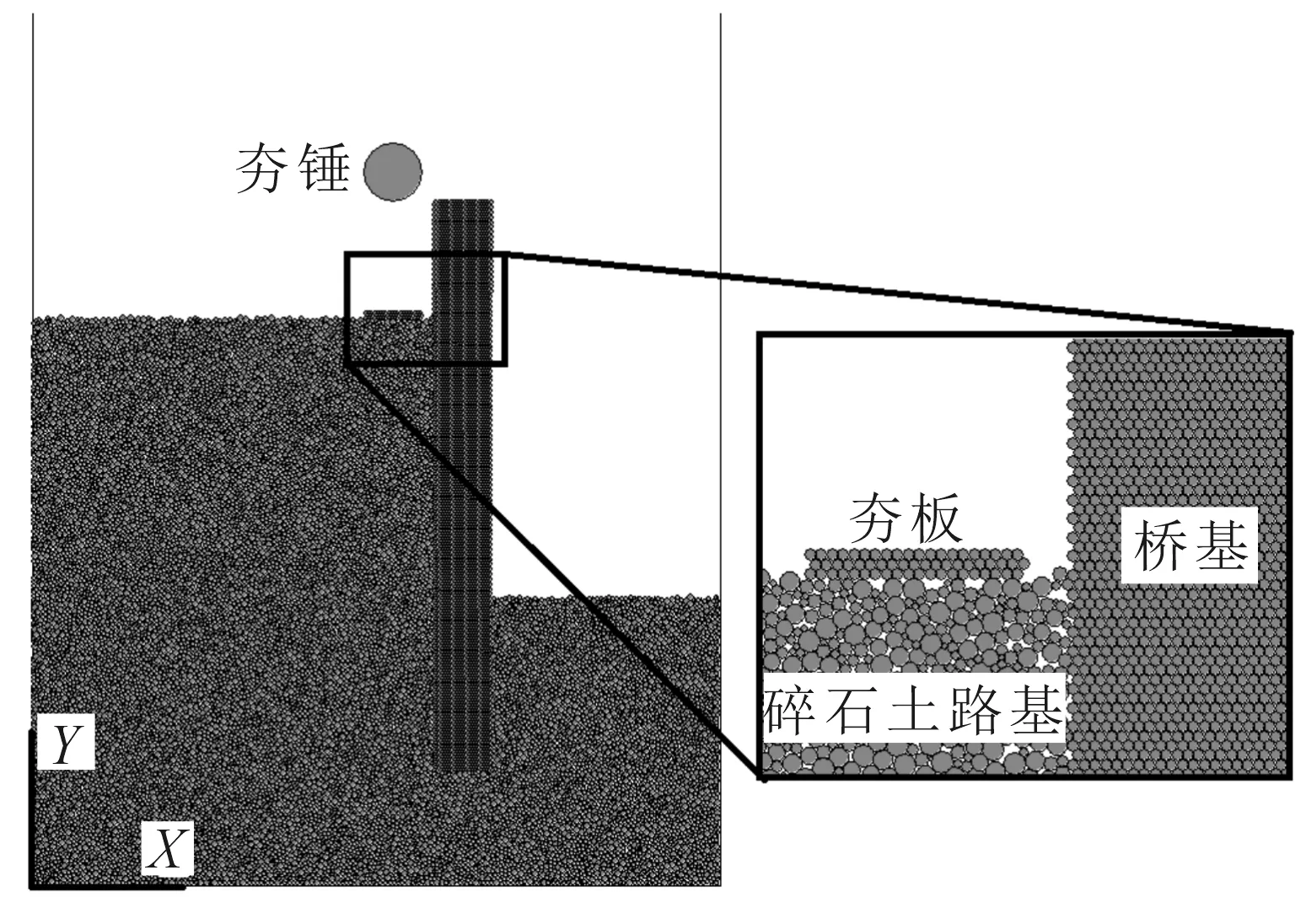
图3　离散元法计算模型示意图

碎石土粒径设置中，因离散元粒径大小直接影响颗粒之间接触点个数从而影响其力学性质，因此如何生成与现场填料相似的颗粒是模拟碎石土相关的力学性质首要解决的问题.现场碎石土粒径跨度的最大粒径约200 mm，最小粒径小于0.075 mm，但现场筛分实验得粒径超过50 mm和小于2 mm的颗粒质量含量较少.软件PFC2D计算中的计算时间增量步长与颗粒最小质量呈平方根关系，颗粒粒径过小严重影响计算速度，故本颗粒流离散元研究中选择生成粒径范围为10～50 mm.

2　计算结果与分析

动力夯实对周围结构影响的主要因素有碎石土的接触刚度、夯击间距、夯击次数、落锤高度、锤重以及夯锤与路基接触形状等，各参数对结构位移作用机理与影响大小也不尽相同.同时轻型夯法设备的应用仍处于初步探索阶段，其施工参数设计缺乏理论论证.为解决部分参数引起的位移量变化难以测量这一问题，采用部分现场实测结果(如关于夯击间距影响下的位移测量)与软件PFC2D离散元数值模拟相对比的方式对各参数进行论证.参数选取如下：① 刚度的选取.离散元法从微观建立模型，颗粒单元间的接触刚度会直接影响碎石土与桥基结构的相互作用机理，进而影响桥基结构的水平位移大小.PFC2D离散元程序采用动力显式计算中若选择刚度过大，则导致为了让各颗粒间的不平衡力满足要求所需的计算时间大大增加；若刚度过小则引起颗粒间的重叠量过大，直接影响到颗粒力学性质以及工程的真实性如使孔隙率过小.法向刚度值的变化幅值在1×106～1×109N·m-1量级之间位移具有较好的收敛性[12]，法向与切向刚度比值选取在1～3之间比较合适[10].故设置法向与切向刚度比值选取为1情况下碎石土的接触刚度参数为2.5×106，5×106，7.5×106，1.0×107，2.5×107，5×107和1×108N·m-1共7组数据，来对比分析碎石土接触刚度对桥基位移的影响.② 不同夯击参数的选取.实际工程中常选取夯击间距为0.3 m，故设置夯击间距为0.1,0.3,0.5和1.0 m，对比夯击间距对桥基位移的影响；此外锤重与落高共同决定夯击能的大小，为与强夯法[1]落高及夯锤重量相区分,结合HHT-3型快速液压夯实机具体参数，将离散元模型中取3 t、5 t、8 t和10 t；考虑到快速液压蓄能器对夯锤的加速效果，落高取3,5,8和10 m.建立相应的模型，从以下几个方面分析各因素对桥基水平位移的影响.

2.1碎石土接触刚度对桥基水平位移的影响

为分析碎石土不同接触刚度对桥基水平位移的影响，将锤重5.0 t、落高5.0 m及夯击间距0.3 m时不同接触刚度情况下，桥基上高度8.0 m位置处12 次夯击后的累计水平位移值，如图4所示，其中x轴取对数坐标，y坐标为动力夯击荷载作用引起的变形量(以下未说明情况下水平位移均为动力夯击荷载引起).

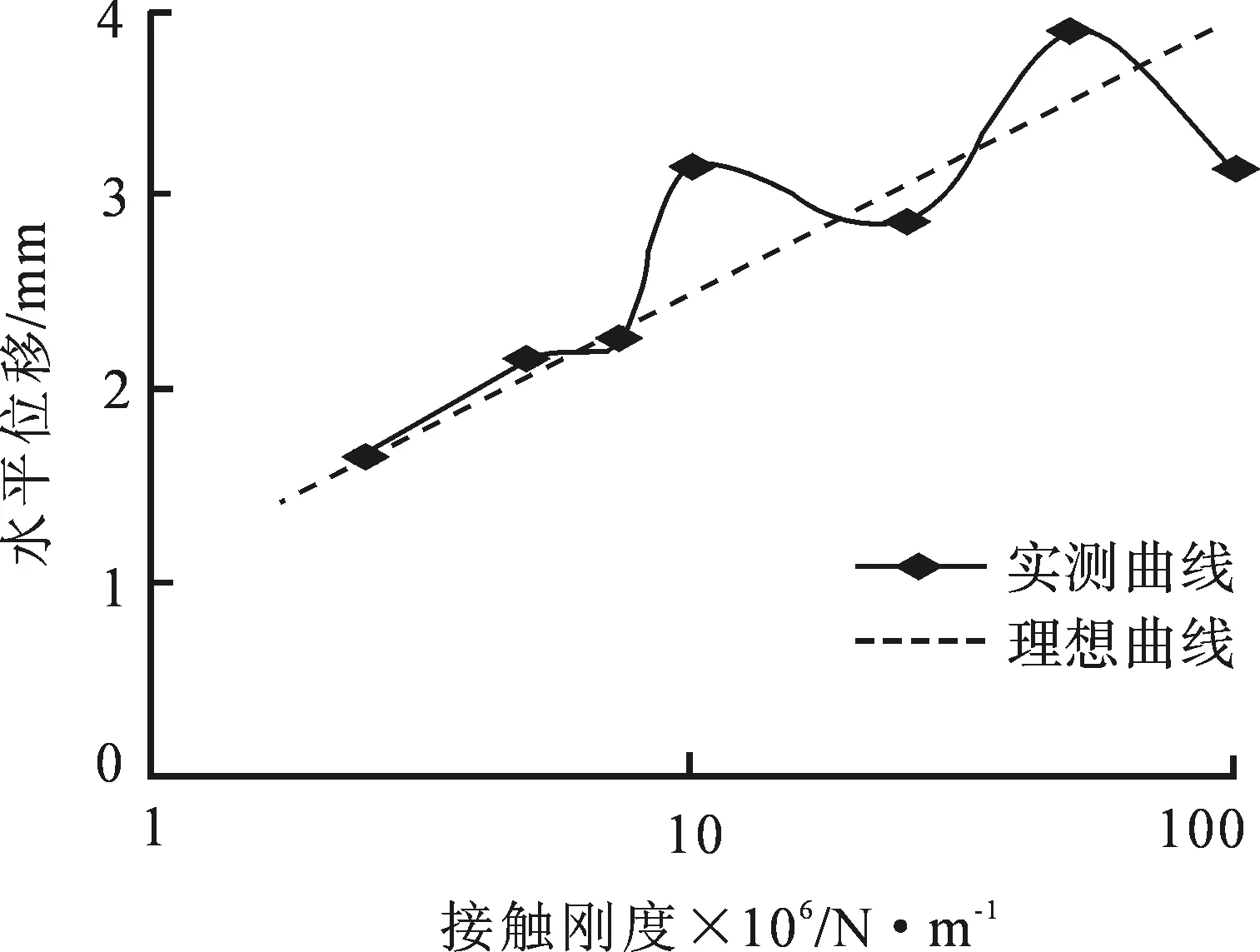
图4　桥基累计水平位移随碎石土接触刚度变化曲线

由图4知，桥基水平位移与碎石土接触刚度的对数值大致呈正比关系.这源于碎石土接触刚度的增大使冲击应力传递效率增加致使更多能量传递到桥基结构上，从而发生更大水平位移；桥基位移变化受接触刚度影响较小，接触刚度为2.5×106～1×108N·m-1，结构水平位移量从1.7 mm增加到3.8 mm；当接触刚度较小时(2.5×106～7.5×106N·m-1)，结构水平位移随着接触刚度稳定增加，而接触刚度较大时(7.5×106～1×108N·m-1)，水平位移量在正比关系线附近发生较大浮动，这说明碎石土接触刚度反映路基土的软硬程度，路基越硬对桥基的位移影响更大；相同工况下的实际水平位移测量为2.7 mm，这与图4中位移值最接近，对应的接触刚度为2.5×107N·m-1，故建议此类工程的接触刚度为2.5×107N·m-1.

2.2夯击间距对桥基水平位移的影响

比较锤重5.0 t、落高5.0 m时不同夯击间距下桥基结构在12次夯击后的累计水平位移的实测值与颗粒离散元法得到的结果，如图5所示，两者位移值的测量点均为桥基上高度8.0 m处.由图5知，实测值与离散元数值模拟的水平位移累计值均随夯击间距的增加呈非线性减小趋势.实测结果在夯击间距0.1 m情况时，取得最大值为3.02 mm.离散元数值计算在0.1 m夯击间距下的最大值为3.2 mm.现场测量值比离散元数值模拟结果小，这是由于实际工程中为减小桥基向临空方向(图3中桥基右侧)产生较大位移而设置了支挡结构，但在本模型中未能考虑此部分支挡结构.

在相同工况下，单次夯击引起水平位移增量的最大实测值和离散元结果对比，如图6所示.由图6可得，两种结果的单次最大水平位移均随夯击水平间距增加呈非线性减小趋势.当夯击间距小于0.5 m，两结果值相差较大且实测值比离散元结果小，在夯击间距大于0.5 m时，实测值与离散元结果曲线近乎重叠.这与现场夯击测试的众多不可控因素有关，如动力冲击荷载的突变性、大碎石颗粒与涵背接触应力集中等.对比图5与图6，说明距桥基的夯击间距是较大影响因素.

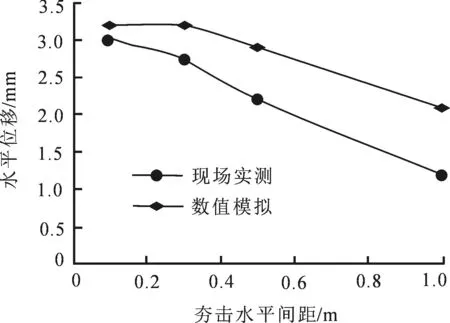
图5　桥基的累计水平位移随不同夯击间距变化曲线

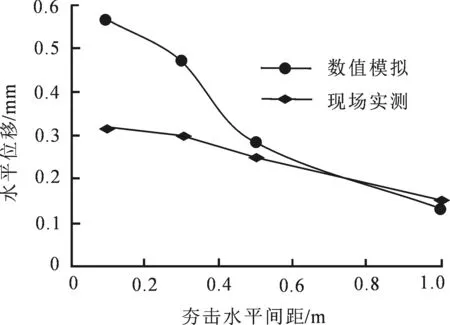
图6　单次夯击桥基水平位移最大值

2.3夯击次数对桥基水平位移的影响

为研究夯击次数对桥基水平位移的影响，锤重5.0 t、落高5.0 m及夯击间距0.3 m时，桥基不同深度处的水平位移随夯击次数变化，如图7所示.桥基整体变形量随夯击次数的增加呈现震荡增加的趋势；随结构深度的增加，位移震荡的剧烈程度和位移累积量均逐渐减弱.

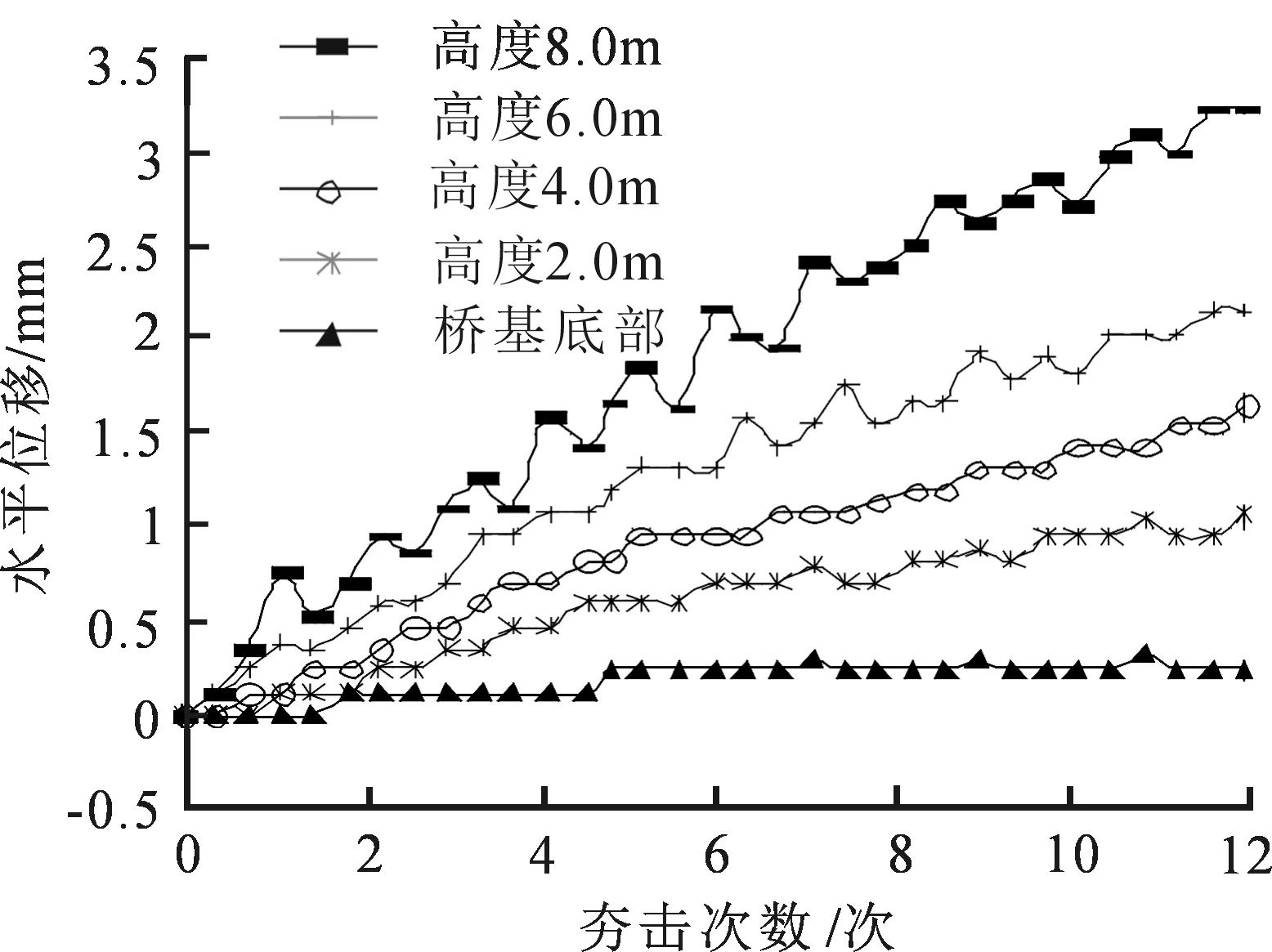
图7　桥基水平位移随夯击次数的变化曲线图

2.4落高与锤重对桥基水平位移的影响

锤重与落高两个因素共同决定着夯击能级的大小和桥基水平位移量.不同锤重与落高对桥基水平位移影响分为三种情况进行分析：① 固定锤重，改变落高；② 固定落高，改变锤重；③ 相同能级情况下的不同锤重.夯击间距为0.3 m，取12次夯击后桥基上高度8.0 m处的累计水平位移量为分析对象.

锤重5.0 t，落高3，5，8，10 m情况下，12次夯击后的累计水平位移量，如图8所示.落高固定为5 m并将锤重设置为3.0，5.0，8.0，10.0 t时，12次夯击后的累计水平位移量如图9所示.由图8～9可知，锤重和落高共同影响夯击能量，说明两者对周围环境的影响机理相似.

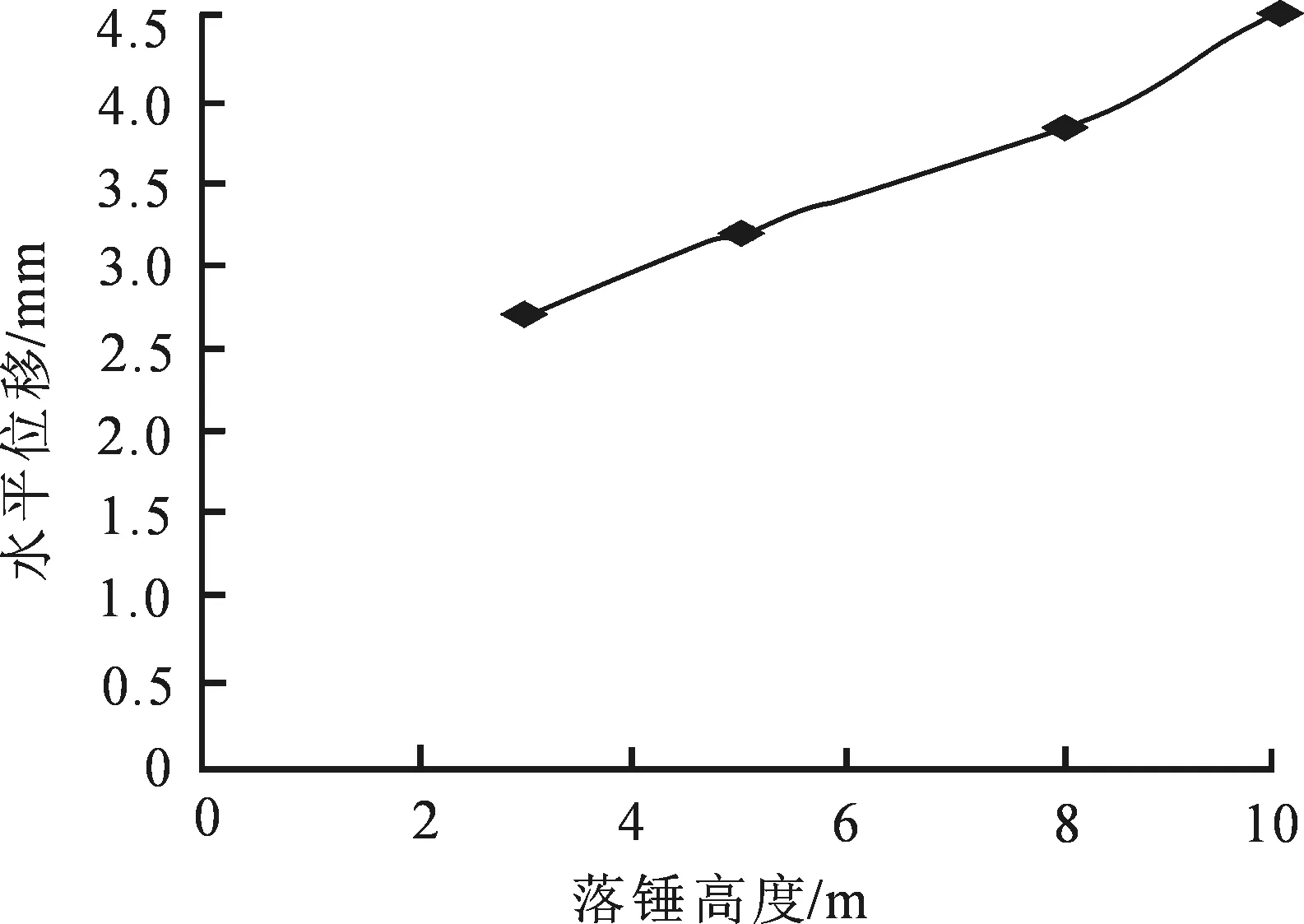
图8　 桥基结构累计水平位移随落锤高度的变化曲线图

为对比同能级下“轻锤高落”和“重锤低落”对水平位移的影响，相同夯击能级下不同锤重时的累计水平位移量见表2.其中夯击能级为150 kJ，位移测点取桥基上高度8.0 m处.

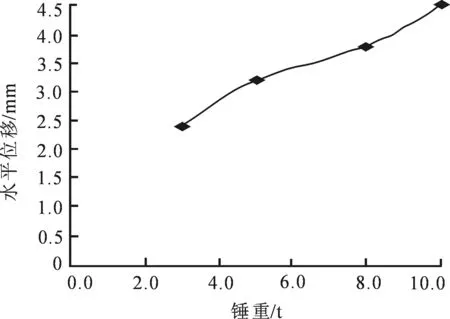
图9　桥基累计水平位移随锤重的变化曲线

表2　相同夯击能级下累计水平位移量随不同锤重的变化Tab.2　Cumulative horizontal displacement under same tamping energy changing with different hammer weight

由表2可见，同能级不同锤重时结构水平位移随锤重增大而增大，说明夯击能级并不是影响位移发展的因素.同能级下“重锤低落”情况，夯锤与土体接触的瞬时速度比“轻锤高落”的结果更小，对结构的影响更为明显.从动量角度分析，同能级下“重锤低落”夯击接触土体的瞬间产生的动量更大，这使颗粒间动量传递向桥基结构，从而对结构产生更大影响.由此可见，动量是影响桥基变形的关键因素，为有效利用夯击能量，建议选用较大的锤重.

“重锤低落”土体在动态状态下所受到的振动持续时间长，这与瑞利波的作用成分占较大比例有关，同时“轻锤高落”对路基的冲切作用更明显，即压缩波和剪切波起到主要作用，后续研究可针对冲击应力波的作用机理对结构水平位移的影响做进一步研究.

2.5接触面形状对桥基水平位移分布的影响

为研究不同夯锤与路基接触面形状对桥基水平位移的影响，如平面和圆面，将是、否放置夯击垫板时，锤重5.0 t、落高5.0 m及夯击间距0.3 m条件下水平位移沿深度分布进行对比.为多方面论证此问题合理性，静止主动土压力作用下的桥基水平位移沿深度方向分布情况，如图10所示.此处x轴为考虑静止土压力作用的总水平位移量.

由图10可知，相同夯击参数情况下，无夯板的圆形接触面的位移量较有夯板更大，这源于圆形夯锤冲击对结构的侧向应力较有夯板时大.有、无夯板时桥基高度8.0 m处的最大水平位移分别为4.1 mm和5.5 mm，表明夯击垫板可使能量较均匀的向下传递并减小对结构物的影响，故工程中建议距结构较近位置的加固施工选择添加垫板方式.

对比分析桥基在理论静止土压力作用下水平位移沿深度分布，结果表明：桥基水平位移量沿深度大致呈分段线性分布，距桥基底部高度2.0 m处为突变点.这是由于距桥基底部高度2.0 m处以上部分恰好为“悬臂”结构；距桥基底部高度8.0 m处的最大水平位移为1.544 mm，此处在有、无夯击垫板时的最大水平位移量分别为理论静止土压力作用下的2.65倍、3.56倍，说明在夯锤的循环冲击荷载作用下增加了桥基结构的水平位移量.

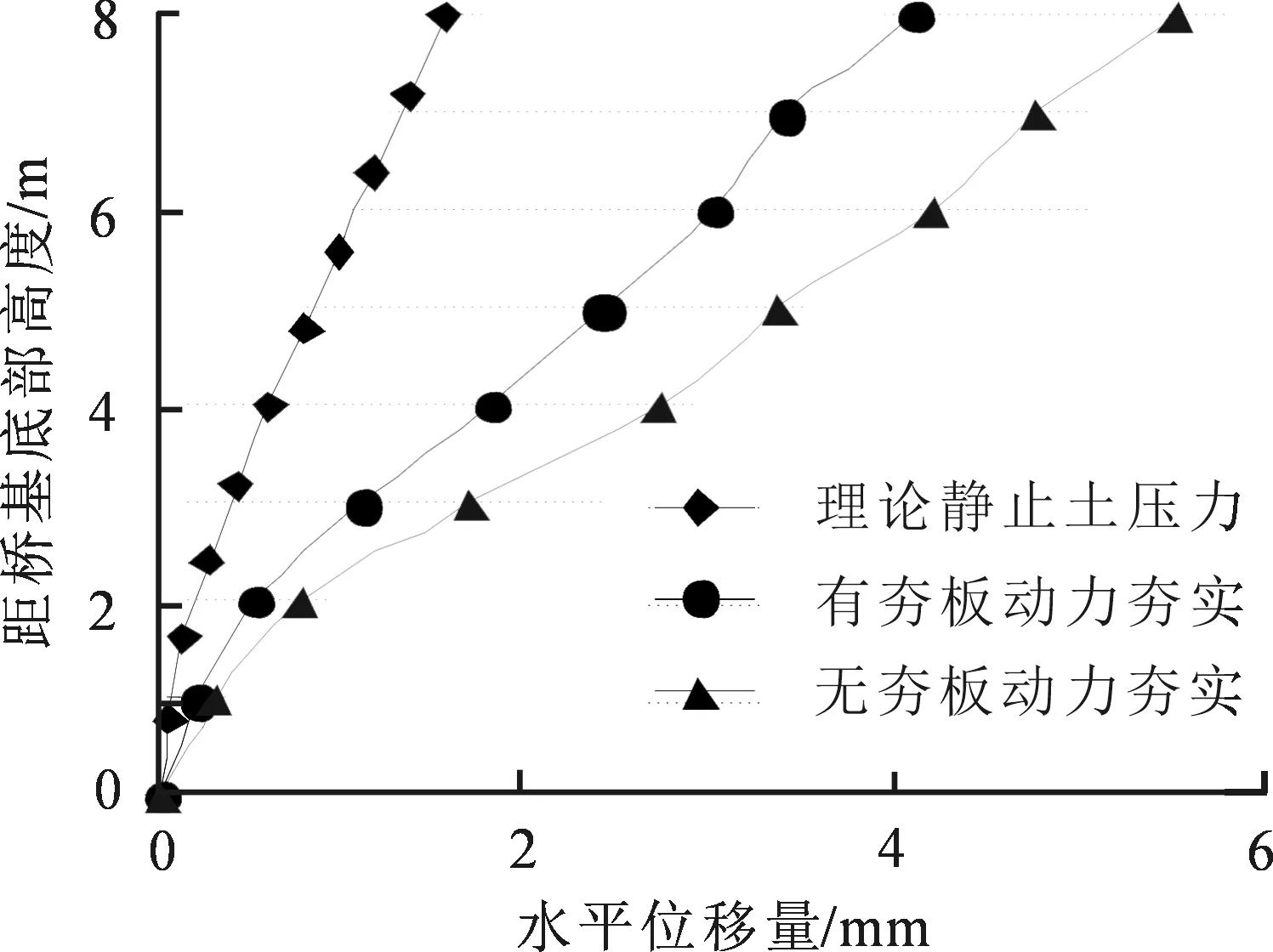
图10　离散元法动力夯实与理论静止土压力下水平位移随深度变化对比

3　结 论

考虑碎石土动力特性，通过离散元软件PFC2D数值模拟桥背回填中动力夯实引起桥基位移的变化规律，对比现场实测值与静止土压力作用下的理论变形值得出结论为

1) 对比分析各种夯击参数对桥基结构水平位移量的影响，夯击间距及接触面形状对桥基结构水平位移量影响较大.相同能级动力夯实条件下，“重锤低落”较“轻锤高落”对桥基结构位移影响大；动量为引起桥基结构水平位移的重要因素.

2) 碎石土接触刚度反映路基土的软硬程度，路基越硬对桥基的水平位移影响越大.桥基水平位移受接触刚度影响不大，且水平位移与碎石土接触刚度的对数值大致呈正比关系.

3) 轻型夯法施工不能忽视动力夯击荷载的循环效应对结构位移发展的影响.动力冲击的不同类型应力波对桥基结构的位移发展作用机理不同，故后续可针对动力夯击荷载的循环效应对桥基结构水平位移的影响及冲击应力波的作用机理做进一步研究.

[1]中国有色金属工业西安勘察院.强夯地基技术规程：YSJ 209—1992[S].北京:中国计划出版社,1995.

Xi’an Engineering Investigation and Design Research Institute of China National Non-Ferrous Metals Industry.Technical Specification of Dynamic Consolidation to Ground Treatment:YSJ 209—1992[S].Beijing:China Planning Press,1995.(in Chinese)

[2]中交路桥技术有限公司.公路工程抗震设计规范:JTG B02—2013[S].北京:人民交通出版社,1990.

CCCC Road and Bridge Consultants Co.，Ltd.Specification of Seismic Design for Highway Engineering:JTG B02—2013[S].Beijing:China Communication Press,1990.(in Chinese)

[3]中华人民共和国机械工业部.地基动力特性测试规范:GB/T 50269—1997[S].北京:中国计划出版社,1998.

Ministry of Machinery Industry of the People’s Republic of China.Code for Measurement Method of Dynamic Properties of Subsoil:GB/T 50269—1997 [S].Beijing:China Planning Press,1998.(in Chinese)

[4]方磊，经绯，刘松玉．强夯振动影响与构筑物安全距离研究[J]．东南大学学报(自然科学版)，2001，31(3):29．

FANG Lei,JING Fei,LIU Songyu.Influence of Vibration Caused by Dynamic Compaction and Safe Distances for Buildings[J].Journal of Southeast University(Natural Science Edition)，2001，31(3):29．

(in Chinese)

[5]朱荣彬，黄亦斌，徐通，等.强夯振动对周边环境影响的监测试验[J].电力建设,2011,32(12):41.

ZHU Rongbin,HUANG Yibin,XU Tong,et al.Monitoring Experiment of Influence of Dynamic Compaction Vibration on Environment[J].Electric Power Construction,2011,32(12):41.(in Chinese)

[6]吴益萍，张天林，王继成.强夯振动数值模拟与现场实测[J].施工技术,2013,42(21):78.

WU Yiping，ZHANG Tianlin，WANG Jicheng.Numerical Simulation and Field Measurement on Vibration of Dynamic Compaction[J].Construction Technology,2013,42(21):78.(in Chinese)

[7]马宗源,徐清清,党发宁.碎石土地基动力夯实的颗粒流离散元数值分析[J]．工程力学,2013,30(S1):184.

MA Zongyuan,XU Qingqing,DANG Faning.Numerrical Study of Dynamic Compacted for Gravel Foundation Using Particle Flow Method[J].Engineering Mechanics,2013，30(S1):184.(in Chinese)

[8]王广月,王登杰,刘健.冲击荷载作用下挡土墙的位移与应力计算[J].山东大学学报(工学版),2002,32(5):437.

WANG Guangyue,WANG Dengjie,LIU Jian.Displacement and Stress of Retaining Wall under the Impact Load[J].Journal of Shandong University (Engineering Science),2002,32(5):437.(in Chinese)

[9]王广月,王登杰.冲击荷载作用下挡土墙上的附加土压力[J].应用基础与工程科学学报,2002,10(2):156.

WANG Guangyue,WANG Dengjie.The Additional Earth Pressure of Retaining Wall under Impact Load[J].Journal of Basic Science and Engineering,2002,10(2):156.(in Chinese)

[10]CUNDALL P A,STRACK O D L.A Discrete Numerical Mode for Granular Assemblies[J]. Géotechnique,1979,29(1):47.

[11]Itasca Consulting Group.Particle Flow Code in 2 Dimensions,Version 3.1,User’s Manual[M].Minneapolis:Itasca Consulting Group,Inc，1998.

[12]魏群.散体单元法的基本原理数值方法及程序[M].北京：科学出版社,1991.

WEI Qun.The Basic Principle,Numerical Method and Program of Symmetrical Dispersed Element Method[M].Beijing:Science Press,1991.(in Chinese)

(责任编辑、校对张超)

Distinct Element Analysis on Bridge Foundation Deformation Caused by Light Dynamic Compaction

YANGFengchun,MAZongyuan,DANGFaning

(School of Civil Engineering and Architecture,Xi’an University of Technology,Xi’an 710048,China)

The impact of light tamping method on the backfill of construction on the deformation of bridge foundation is analyzed.By using the distinct element method,the impact on the horizontal displacement of bridge foundation under different factors,such as the gravel soil contact stiffness,the weight of hammer,the height of hammer,the horizontal spacing of hammer is simulated,and the change rules are found.The measured values of horizontal displacement of bridge foundations during the process of dynamic tamping are compared with the theoretical values under static backfill earth pressure.The result show:The horizontal spacing of hammer has greater effect on the displacement of bridge foundation;Under same tamp energy,“light hammer at lower height” achieves a smaller horizontal displacement than “heavy hammer at higher height”.The maximal displacement deformation of bridge foundation under the action of tamping with or without a tamping plate is 2.65 or 3.56 times of that under static backfill earth pressure,respectively.

distinct element;deformation of bridge foundation;light dynamic compaction;

10.16185/j.jxatu.edu.cn.2016.08.006

2016-04-20

国家自然科学基金(51279155)

杨丰春(1989-)，男，西安理工大学硕士研究生.

马宗源(1980-)，男，西安理工大学讲师，主要研究方向为岩土力学.E-mail:mzy_gogo@hotmail.com.

�

A

1673-9965(2016)08-0634-07