数字矿山技术进展

王李管，陈 鑫



数字矿山技术进展

王李管1, 2，陈 鑫1, 2

(1. 中南大学资源与安全工程学院，长沙410083；2. 中南大学数字矿山研究中心，长沙410083)

数字矿山概念作为国家战略“两化融合”在矿产资源行业的应用，对新常态下矿山企业发展影响越来越深。本文结合矿山企业生产过程的特点，给出数字矿山的具体概念，并以数字矿山领先技术和应用为线索，概述了矿山资源评价与建模、开采规划与优化、数字化采矿设计，以及生产管理与安全管控的新技术与新发展，指出信息化智能化发展的技术革新以及应用前景，对矿山企业的未来发展提供了富有成效的建议。

数字矿山；三维可视化；资源模型；规划与优化；数字化设计；智能管控

矿业是国民经济发展的支柱产业，自20世纪90年代中期以来，我国矿产资源产量与GDP保持正相关同步增长。随着经济的持续发展，产业结构的深度优化，资源再利用水平的逐步提高，未来数十年中，我国原生矿产资源的消耗强度将达到最高峰，随后将缓慢降低并维持在一定水平。由于我国主要金属矿产资源总体赋存条件差、单体资源规模小、品位低，再加上近十年来以投资和价格拉动为主要特征的经营模式，导致矿山开采技术并未取得实质性的突破。目前，在市场价格低迷的情况下，我国矿业行业面临产能过剩、效益低下，安全和环保形势严峻。

从发达国家采矿业的发展历程来看，采矿技术进步起始于作业工具的机械化，发展于单台设备的自动化、独立系统的自动化，完成于整个矿山生产过程的自动化[1]。从1892年以来，对不同采矿技术条件下劳动生产率的统计结果表明，从人工生产到全自动化生产演变过程中，全员人均劳动生产率从1000 t/a将增长到7500 t/a。毋庸置疑，采矿工具与技术的变革是我国矿山企业升级转型的必经之路。

近年来，尽管政府、企业、大学和各类研究机构在数字矿山技术领域开展了大量的研究工作，并取得了可喜的进展，但从系统性、实用性等方面来看，仍处于起步阶段[2]。数字矿山技术从资源评价与建模上着重研究结构建模、属性建模和模型更新关键技术，从开采规划与优化上涵盖开采单元优化布置、境界优化、中长期计划和短期计划优化，从数字化采矿设计上主要解决损失贫化控制和数字化开采设计，从生产管理与智能管控上沿着按需通风与调控、虚拟管控、生产执行和智能调度的轨迹提升，以改变企业的运营模式，实现行业的技术转型与升级。

1 数字矿山体系结构

与加工制造行业相比，矿山企业生产过程具有如下特点[3]：第一，对生产对象(资源)的认识是一个循序渐进的过程，矿石资源的空间形态、品位分布、控制程度、市场价格等对企业的生产过程和经济效益具有重大的影响；其次，生产场地分散、生产工序繁多、作业过程不连续，新的作业点不断形成的同时老的作业点也在不断消失，危险源分布范围广、风险高、突发事件难以预测，经济效益和生产安全之间的矛盾十分突出；最后，开发过程产生的废料多，无害化处理难度大，开采本身对环境造成的破坏难以避免，环保风险高。

矿山企业生产过程的独特性，决定了矿山信息化过程的复杂性和难度，也衍生出了矿山信息化的专有概念—数字矿山。数字矿山是指以矿产资源开采过程相关数据为基础，对资源、规划、设计、生产和管理进行数字化的建模、仿真、评估和优化，并持续应用于矿山生产全过程的新型矿山技术体系和生产组织方式。

数字矿山综合考虑矿山地质、测量、采矿等生产环节的技术特点，借助地质统计学理论、最优化方法、可视化仿真技术、软件技术、网络技术和自动化技术，构建三维地质模型和资源价值模型，优化开采方案、采矿设计和生产计划，监控和管理采矿生产过程，保障矿山生产安全，降低矿山经营风险，提升矿山综合竞争力。数字矿山的出现给矿山的生产技术和管理模式注入了新的活力，带动了技术规范、标准、流程和方法的革新。

2 资源评价与建模

2.1 结构建模技术

数字化采矿设计系统中，结构建模主要对地表、矿体、井巷和空区等实体进行几何建模，以准确表达实体的外部轮廓边界、表达实体间空间关系，从而做到准确设计、精确出图的目的。结构建模涉及到的关键技术与算法主要有DTM建模技术、轮廓线拼接建模技术、体数据等值面建模技术、基于中心线—断面三维构模技术和基于点云数据三维表面重建技术等。通过以上一种或几种算法和技术的综合应用可以解决矿山三维表面模型构建的绝大部分问题，如地面模型建立、复杂矿体建模、井巷工程建模、岩层建模、断面建模、露天矿坑建模，及采场和采空区建模等。

约束Delaunay三角剖分(CDT)是实现DTM建模的基本算法，CDT是指对点集进行剖分时，应满足某种约束条件，如对象重建中的模型边界、地表模型中的山脊线、山谷线、断裂线等。构建CDT的算法通常采用两步法：第一步构建常规DT剖分，第二步再将约束边强行嵌入到三角剖分中。JONATHAN等[4]采用连续的对角线交换算法实现约束边的嵌入；PAUL等[5]提出的算法是在所有点Delaunay三角化完成后，对约束边通过的三角形进行调整，使之满足约束Delaunay三角形的条件；JOACHIM等[6]采用增量式方法构建三角网，然后对“受影响”三角形区域进行三角形重构，实现约束Delaunay三角剖分。综合各算法的技术特点，可归纳出其建模步骤主要包括增量式Delaunay三角剖分、恢复约束边和建立地性特征线约束，建模效果如图1所示[7]。

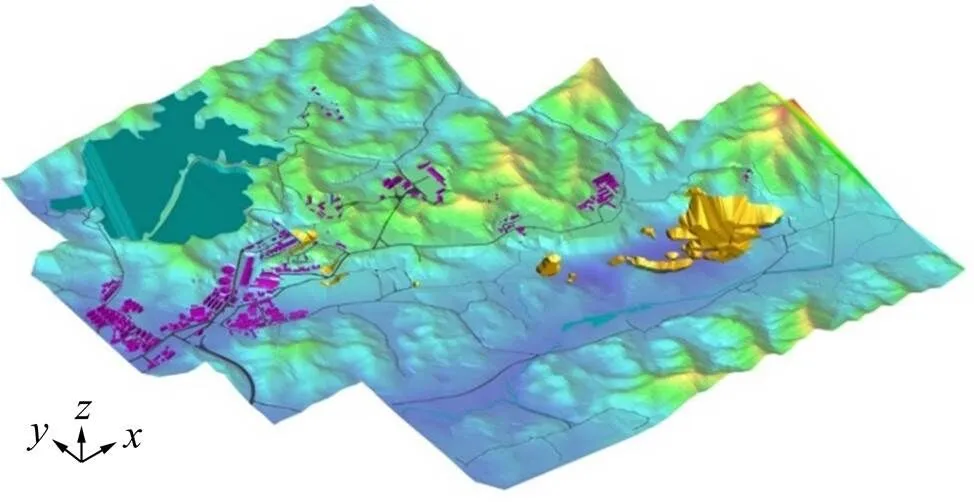
图1 DTM建模效果图[7]

矿体建模算法主要包括轮廓线拼接法和体数据等值面法。轮廓线拼接法通过轮廓线关键点为顶点的三角面片，将每层轮廓线连接起来，拼接出物体的表面[8]。该方法首先遇到的问题是轮廓线对应问题，即确定相邻层面上的轮廓对应关系。由于约束不足，轮廓对应存在很大的任意性。当相邻层面上轮廓之间的错位很大时，对应问题就变得愈发难以解决，轮廓拼接的关键在于确定对应轮廓线上点之间的对应关系，该对应关系主要包括两类形式，一类是对应轮廓线上每个点的出度与入度均为1，如图2(a)所示；另一类如图2(b)所示，即对应轮廓线上某个顶点的出度与入度不为1，其他各顶点的出度与入度均为1。大多数应用中一般只接受第一类对应关系，对应关系确定后用三角形面片拼接表面。

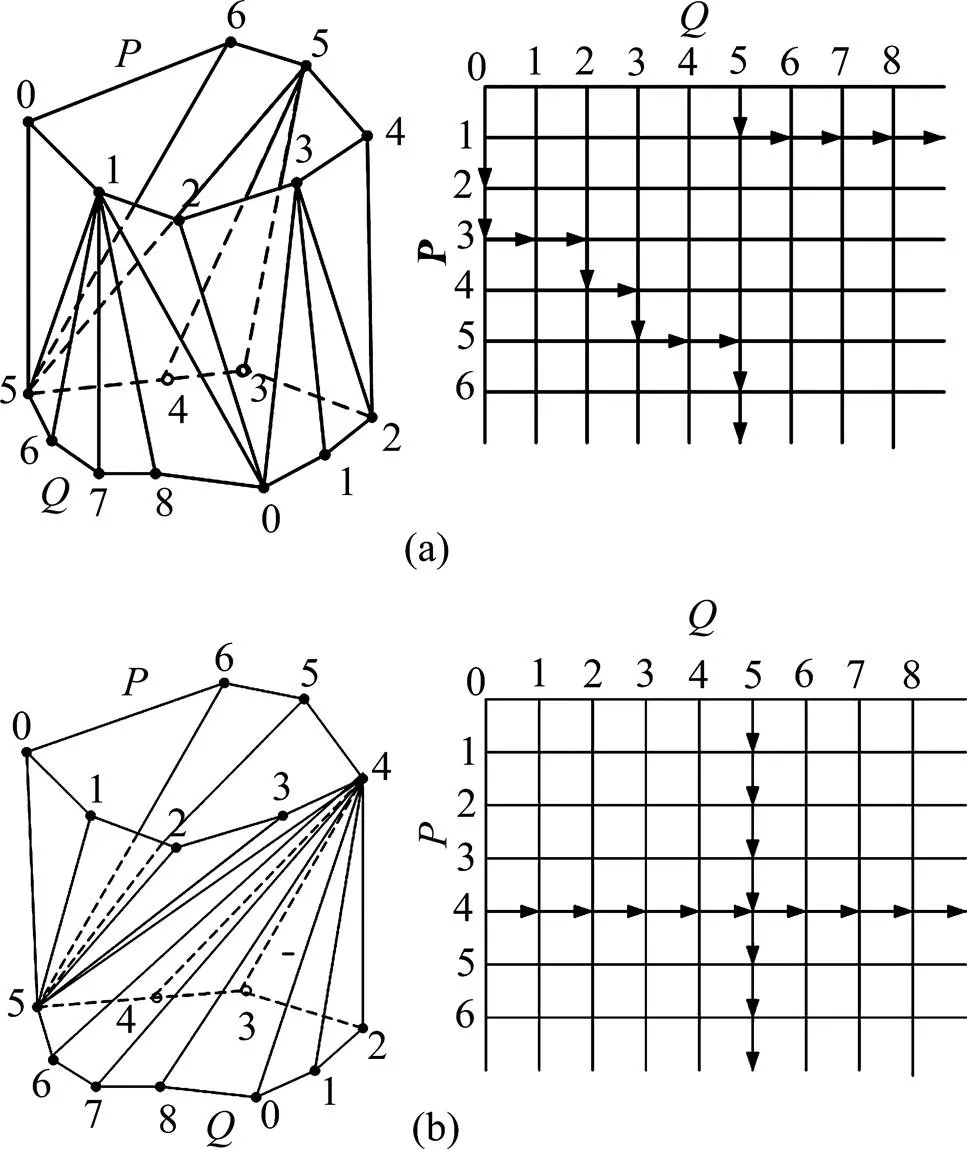
图2 轮廓线顶点对应关系

轮廓线拼接法对于较为复杂的矿体轮廓线都可以得到较为理想的结果，并且可以与轮廓线严格吻合。但这种方法每次都是通过两两轮廓线重建表面模型，没有从整体上把握矿体的形态；而且在处理不同层面上的轮廓线之间的对应问题和分支复合问题大都通过人工交互的方式进行，比较费时，且随意性很大，难以实现自动三维表面重建。GLANZING等[9]提出的体数据等值面法，将轮廓线间的表面重建问题转化为体数据中的等值面构造问题，得到的重建表面能精确地呈现相邻层面间对应轮廓线的形状的渐变；而且该算法可以避免轮廓对应、分支关系的判断；其缺点是数据量和计算量较大，在轮廓线突变出不能很好吻合。在实际应用中，如果对矿体表面的重建精度要求较高、相邻层面上的轮廓形状相差比较大、分支复合的情况较多时，或者要求自动三维表面重建时，可以采用体数据等值面法来完成表面重建。

通过等值面和场函数实现地质体自动建模技术，解决分支复合比较严重的复杂地质体自动建模难题，基本建模步骤为：通过轮廓线和场函数构造体数据；基于体数据构建规则体数据场，并提取规则体数据场等值面；根据等值面建模形成最终三维表面模型。针对其计算量较大、表面重建速度慢的缺点，在分析产生这些缺点原因的基础上，采用距离函数作为场函数，并采用距离变换中的构造体数据，通过扫描法及距离传递加快计算速度，同时采用分治法满足轮廓线间距不一致的特点，以及降低内存需求，选择移动立方体算法进行等值面构造，并对重建的表面模型通过边折叠算法进行简化处理。

由于每个体素有8个顶点，每个顶点可能有0、1两个状态，分别表示顶点为于等值面外和位于等值面内，因此每个体素按其8个顶点的0、1分布而言，共有256个不同的状态。分析立方体体素两种不同的对称性，可以将256种不同的情况简化为15种，如图3所示[10]。

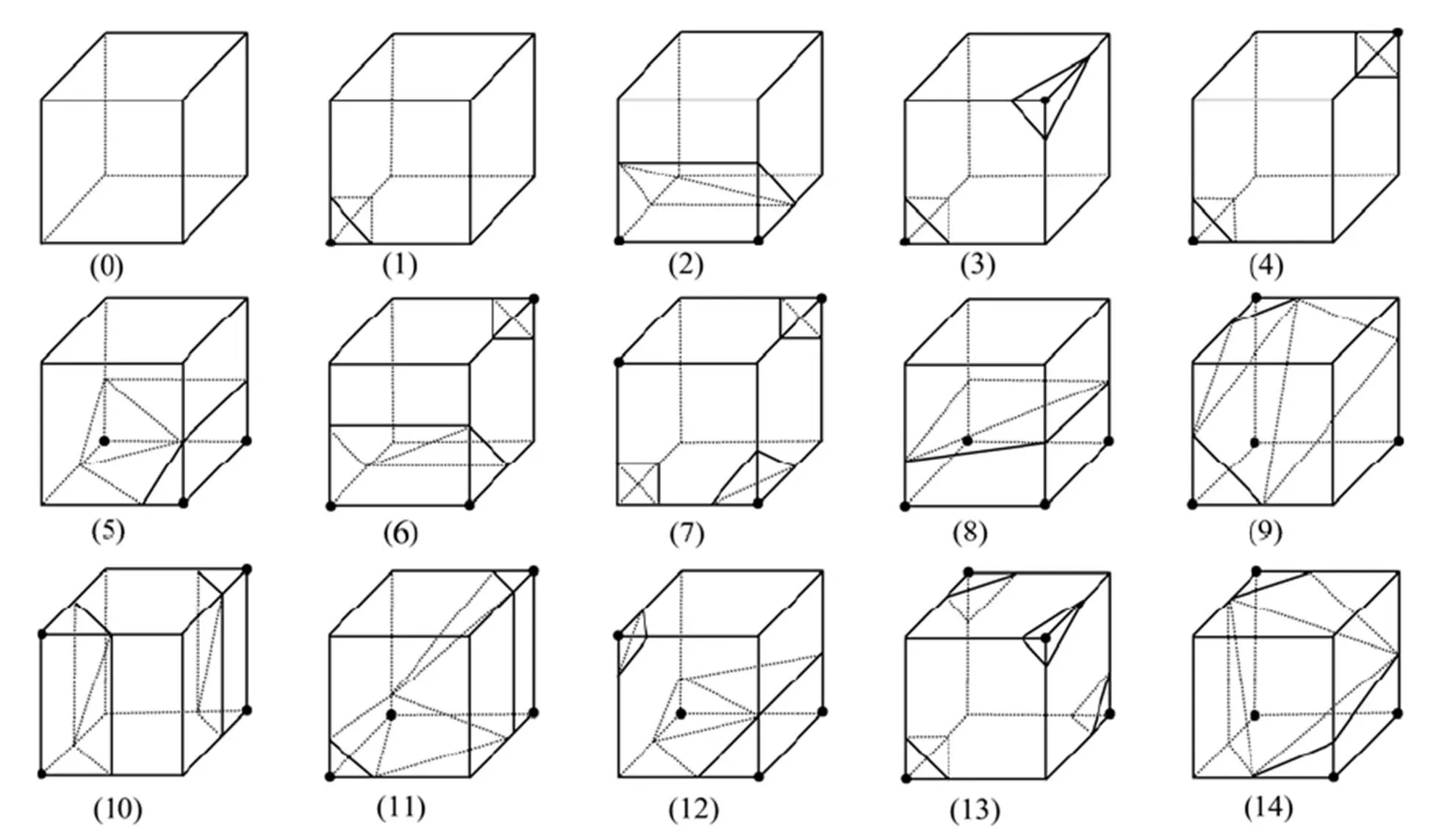
图3 体素中等值面的15种基本构型[10]

CONGOTE等[11]]通过分析基本体元状态模型，提出在立方体的一个面上，如果位于等值面内外的顶点分别分布在对角线的两端，就存在两种连接方式；当相邻的两个立方体在公共面上采取不同的连接时，就会出现孔洞。相邻的两个体元，它们的邻接面存在二义性，如果在各自体元内，面与等值线的交线不一致，所构造的等值面会出现孔隙。

四面体剖分算法能够解决拓扑二义性，但CIGNONI等[12]提出四面体剖分算法中等值面的构造与剖分方式有关，如果相邻立方体单元剖分不一致同样会产生裂缝。另外，在立方体内的等值面没有二义性时，立方体也会被剖分处理，大大增加了算法的时间复杂度，因此较少应用。

NIELSON等[13]提出使用双曲线渐近线算法来解决面上的二义性，等值面与立方体某一面的交线是一组双曲线或者其中的一支。当两支双曲线都与立方体表面相交时，就会出现二义性，此时两支双曲线将立方体表面分成3个区域。可以证明，双曲线渐近线的交点总是和其中一对交点落在同一个区域，比较渐近线交点和等值面的标量值，若渐近线交点的标量值大于等值面的标量值，则标量值大于等值面标量值的一对顶点与该交点落在同一个区域；反之亦然。基于体数据等值面法建模效果如图4所示[14]。

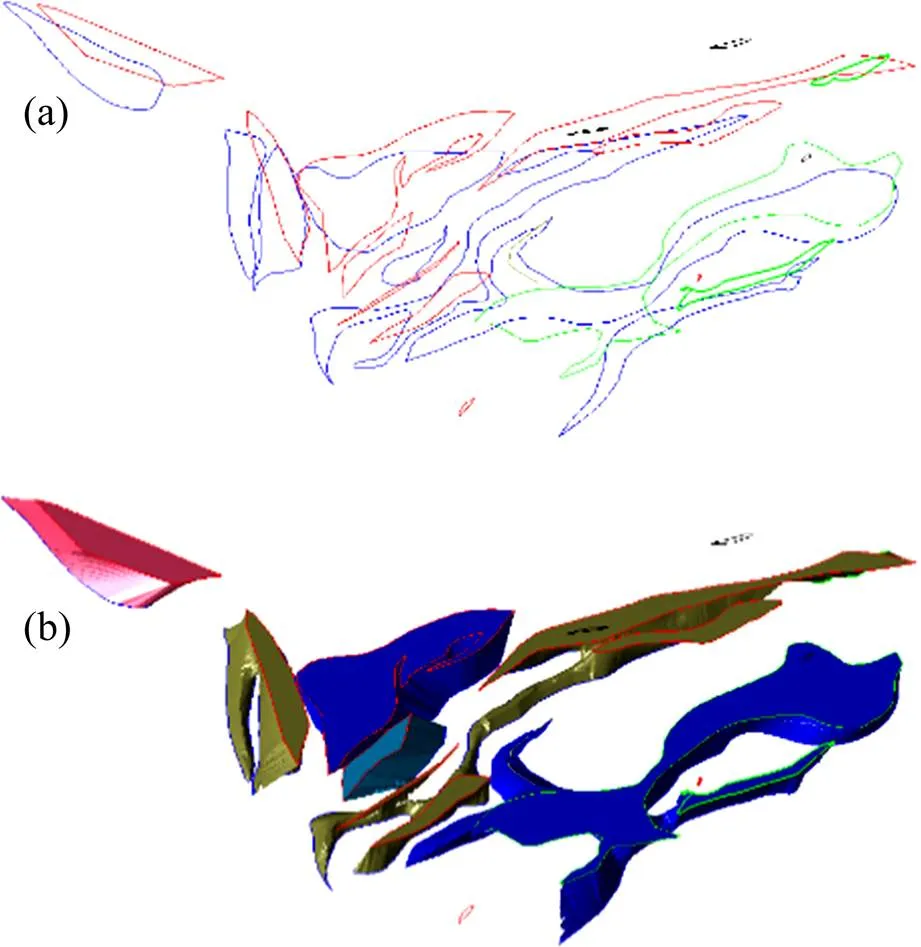
图4 体数据等值面法建模[14]

计算机图形学领域有一类物体，可通过一系列的轮廓线来建模，这一系列的轮廓线每个都有自己的变换，并逐个连线框形成管状的三维实体，该理论奠定了井巷工程建模的基础。如图5所示，沿中心线在每个选中的点上建立局部坐标系：局部轴指向沿着中心线方向，局部轴和局部轴指向与轴垂直。轮廓线在平面上，需要确定每个轮廓线的顶点。采用局部坐标系和空间坐标系转换的方法，其关键是计算局部坐标系到空间坐标系的变换矩阵。

图5 沿中心线建立局部坐标系

当中心线上控制点处轮廓线生成好后，就可以将这些断面轮廓线拼接为不规则三角网。由于巷道的断面形状比较规则，因此，生成断面轮廓线之间的三角网格相对比较简单。

地下巷道建模的难点在于交叉处的处理，如图6所示，交岔点的平面尺寸主要根据运输设备的类型、线路的布置及人行安全等要求确定，在设计前，各分支巷道断面及主巷与支巷的关系已经确定。因此，交岔点平面尺寸的已知条件应为：所选道岔的参数、、、，支巷对主巷的转角，各分支的净宽度1、2、3及其轨道中心线至柱墩一侧边墙的距离2、3等值，采用固定斜墙斜率的方法确定扩大部分墙的位置。

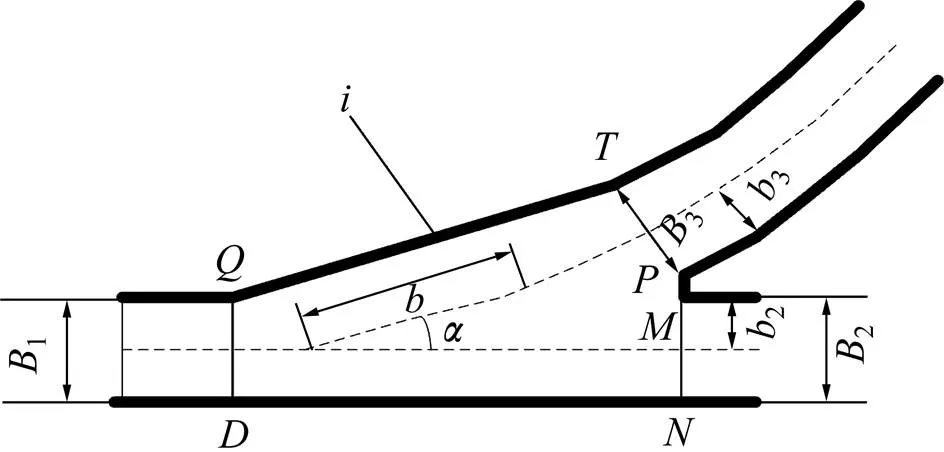
图6 巷道分岔点示意图

交叉处建模关键过程为：根据中心线的断面属性，获取断面的墙高、拱高/底宽比，并以、、、为底边，建立断面轮廓线0、1、2和3；采用单一巷道实体的建模方法，生成轮廓线0和1之间的巷道实体，效果示意图见图7；连接，分别对多边形、和实现快速多边形网格三角化；合并所有的三角网格，生成交岔点三维实体模型。

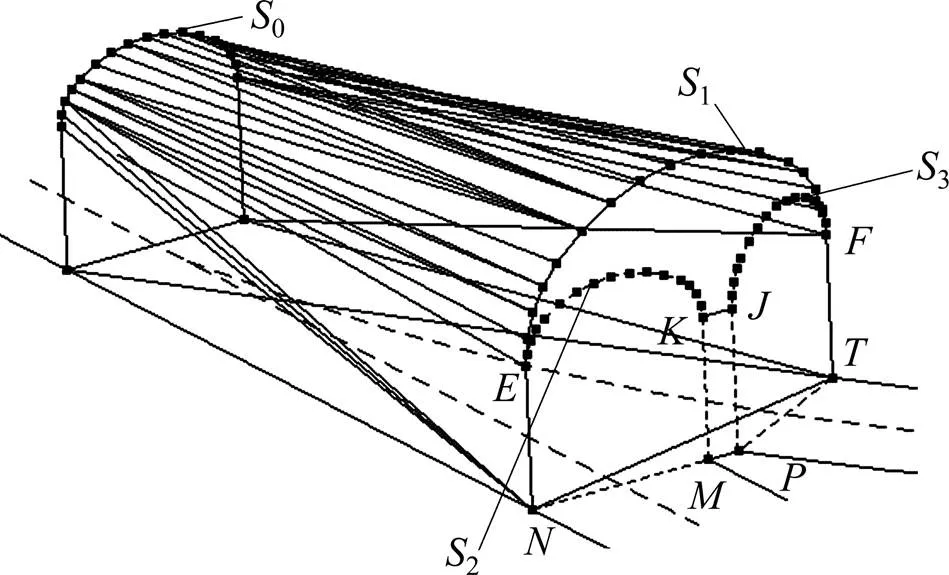
图7 巷道交岔点三角化

近年来，随着激光测距技术的发展，三维激光扫描技术也逐步应用于矿山领域，它是一种采用非接触式的高速激光测量方式，以点云形式获取被测对象表面的阵列式几何图形的三维数据，针对矿山采空区的探测，三维激光扫描仪扫描的结果只是采空区表面的点云数据，在应用中需要更具有实际意义的三维实体表面模型，点云数据的直接建模算法主要分为三类：隐式曲面法[15]、区域生长法[16]和Delaunay三角剖分法[17]，直接建模算法由于未考虑扫描点云数据的特性，故在实际应用中效率较低。

结合三维激光扫描的特性来研究间接的点云数据建模算法，郑顺义等[18]提出了将局部邻近点投影到切平面进行建模，再拼接成整体，该方法的结果依赖于邻域大小的选取，且容易造成表面空洞和面片重叠等构网错误；张帆等[19]提出了基于球面投影的构网算法，将点云数据投影在球面上对其构网，该方法实现复杂且时效性有待改进，本文作者[20]提出了一种基于半球面-平面联合投影的激光扫描点云数据建模算法，可较好的解决空区扫描点云数据建模问题，其算法流程及建模效果如图8和图9所示。

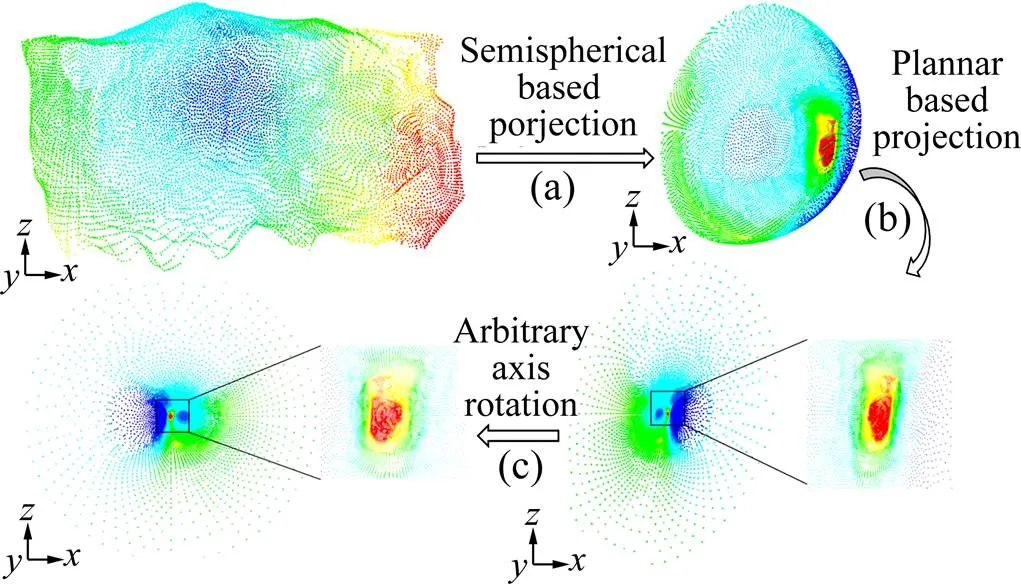
图8 半球面−平面联合投影

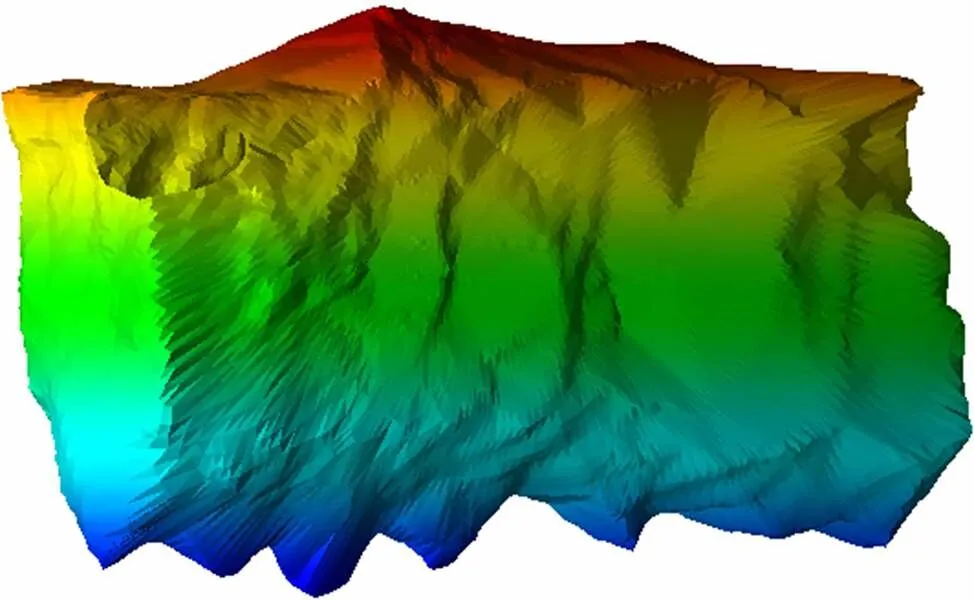
图9 采空区建模效果图

2.2 属性建模技术

属性模型通过体元记录矿山地质体内部物化信息，体元模型的数据量与其分辨率成正比，数据量大及处理时间长是体元模型的共有特征。地学领域的研究范围或对象都比较大，分辨率高，而且属性分布不均匀，通常采用八叉树模型进行结点合并与压缩，其结点数量十分庞大，因此，海量数据是真三维地学建模遇到的关键问题之一。近年来，随着三维地学属性数据获取与生成手段的快速发展，海量数据问题日益突出。八叉树模型一般在内存中构造，将指针概念推广到外存，采用外存指针对海量八叉树结点数据进行组织和管理。属性建模技术主要研究外存八叉树模型的构建技术、基于属性模型的结构模型的快速栅格化算法、属性模型的查询技术、属性模型的可视化技术，其中属性模型的构建算法与结构模型的栅格化算法实现结构模型与属性模型之间的转换。

基于八叉树的块段模型不同于传统块段模型，其建立过程中不需要对原型进行初始栅格化，只是对三维目标的空间位置进行栅格化，这样可以大大避免冗余数据的产生，同时没有基本单元块的限制，这样不同的地质目标可以有不同的体元粒度，实现多分辨率的要求。构建过程分为构造原型和目标赋属性两个步骤，如图10所示[21]，其中目标赋属性就是对属性模型中目标范围内的三维空间栅格化，对每个体元赋上相应的属性，体元的大小可以根据目标的规模以及属性记录的精度要求而定。

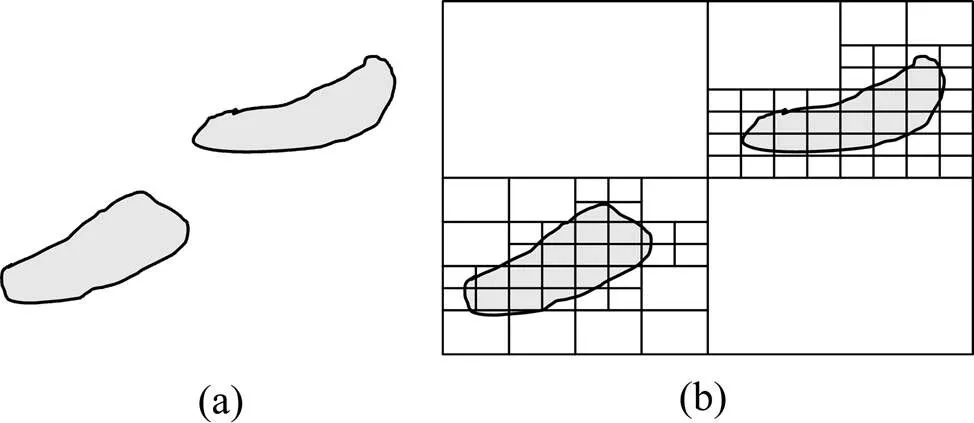
图10 基于外存八叉树的属性模型[21]

基于属性模型的结构模型栅格化是区域属性查询的基础算法，也是属性模型可视化表达的重要手段。在数字采矿软件实际应用中涉及到大量的属性查询及可视化表达，对于数据量可能达到TB级的属性模型，速度、内存及正确性是应该重点考虑的问题。

结构模型栅格化源于多面体离散化，所谓离散化就是用有限个三维单元体将多面体完整的充填起来。根据采用的单元体不同，目前常用的充填方法有六面体充填和四面体充填，分别称为六面体化与四面体化。为了很好的拟合结构模型的边界和表达属性模型的属性值，可以将六面体规格取得很小，但这样会大大增加数据量，实际上在模型内部可能存在相邻体素属性值一样或在某一个较小容差范围之内，因此可以将它们合并处理，从而减少数据量；另外，如果一个结构模型所表示的矿体范围很大，则栅格化以后六面体个数很多，如果用传统的六面体表示法，每个六面体用8个坐标点表示，需要大量内存空间。基于以上原因，为了能够有效地进行合并处理及降低结果数据量，毕林等[22]提出自适应虚拟八叉树的概念并引入一种新的三维数据类型−半结构化格网，六面体尺寸分别为4 m×4 m×4 m、2 m×2 m×2 m和1 m×1 m×1 m时，栅格化耗时相应为2.51、5.95及32.59 s，不同尺寸栅格化效果如图11所示。

图11 基于属性模型的结构模型栅格化[22]

2.3 模型更新技术

由于采矿对资源的认识是一个循序渐进的过程，伴随着开采过程中获取的更加精确的资源分步信息，需要将其更新至已有工程，从而保障信息的一致性及实时性。

井巷工程的模型更新方法主要有步距法、断面法和双线法。采用步距法测量巷道时，首先以具有精确三维坐标的两点布设工程的施测主线，然后在不同主距刻度上以垂直主距方向量取左、右帮距的测图方法，对于工程交叉位置，量取一边帮距，另一边帮距沿用上一步距同边帮距。在能得到测量主距起止坐标的工程一般多采用步距法。根据步距法实测数据建立地下巷道三维模型的基本原理是：两测点以及两测点的连线确定了巷道的走向，通过左帮、右帮距离、巷道高度以及提供的断面属性信息，拟合出各断面轮廓线，然后采用单一巷道体建模方法实现实测巷道的三维建模，如图12所示[23]。

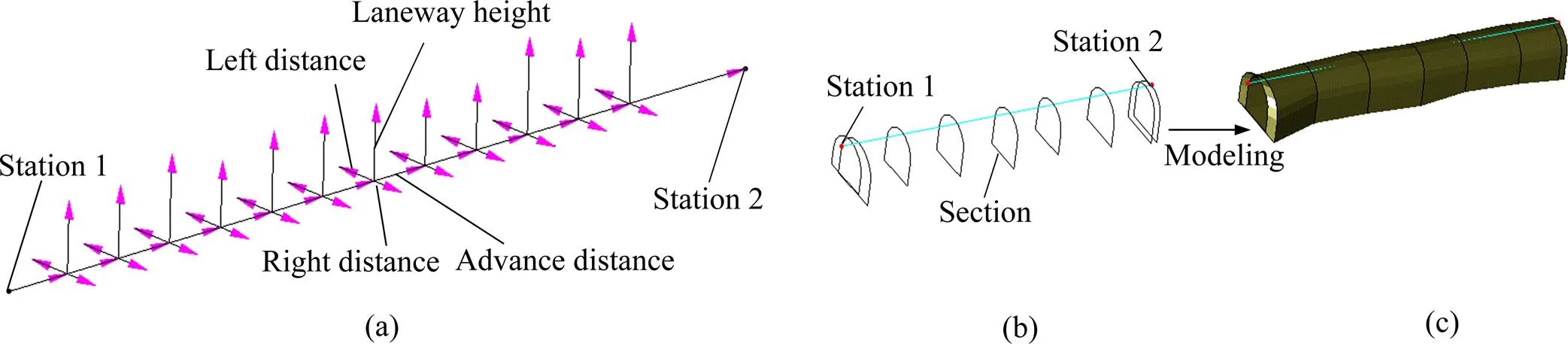
图12 步距法示意图[23]

采用断面法进行巷道测量时，将全站仪放置在巷道不同位置，测量各断面轮廓线上的点。断面法测量巷道过程见图13，图中黑点表示测量的点。根据断面法实测数据建立地下巷道三维模型的基本原理是：判断哪些实测点处于同一断面上，并根据同一断面上的实测点建立断面轮廓线，然后采用单一巷道体建模方法，实现实测巷道的三维建模。

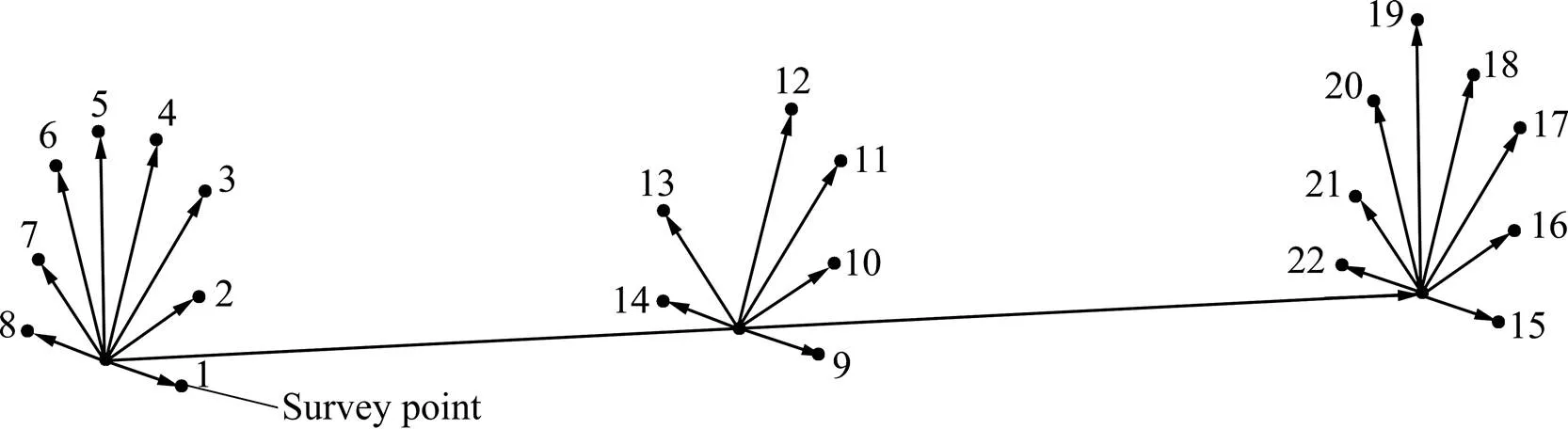
图13 断面法示意图

双线法是多数金属矿山较常采用地下巷道测量方法，通过测量巷道底板边界线，来形象描述各中段巷道底板宽度信息和巷道间的贯通情况，基于实测底板边界线的巷道三维建模更接近实际情况，建模相对复杂且更具一般性。谭正华等[24−25]采用约束三角剖分的方法生成巷道模型的上下底盘面，利用两段成面法生成巷道模型的侧面，最后将这些面组合成巷道模型，该方法难以解决常见的圆弧拱、三心拱等断面的巷道建模问题，在此基础上设计了一种基于实测底板边界线和断面形状三维巷道实体建模算法。巷道的边界将所在的中段面划分为若干封闭区域，如图14(a)所示。采用区域树形式化表达和存储底板边界所划分的区域，区域树的每个结点代表一条有方向的多边形；然后采用约束三角剖分的方法将各区域网格三角化，如图14(b)所示，提取三角形中表示出口和断面底板的边，根据给定断面生成断面轮廓线，然后均匀离散化各断面轮廓线，生成表示实体巷道的特征点，最后分层提取特征点，生成巷道实体的分层轮廓线，并对相邻轮廓线和顶、底轮廓线分别网格三角化，如图14(c)所示。

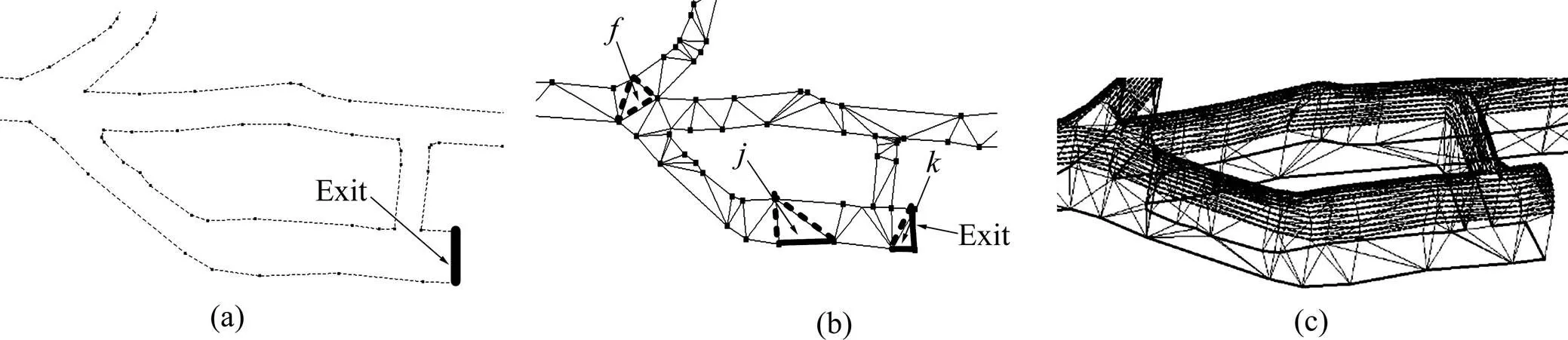
图14 基于实测底板边界线和断面形状三维巷道实体建模

矿体模型主要通过平剖面轮廓线信息实现模型更新，通过平剖面轮廓线网格划分、网格曲面构建和网格曲面拼接等技术，可解决基于生产勘探数据的地质体自动建模与更新，基本建模步骤为：计算轮廓线质心和法向量，确定轮廓线剖面；建立轮廓线包围盒，使用轮廓线剖面切割包围盒得到若干切割体，提取各切割体上附着的轮廓线作为网格；使用CONS曲面或NULLBS曲面技术实现单个网格的建模；将各建模后的网格拼接形成最终三维表面模型，如图15所示[26]。

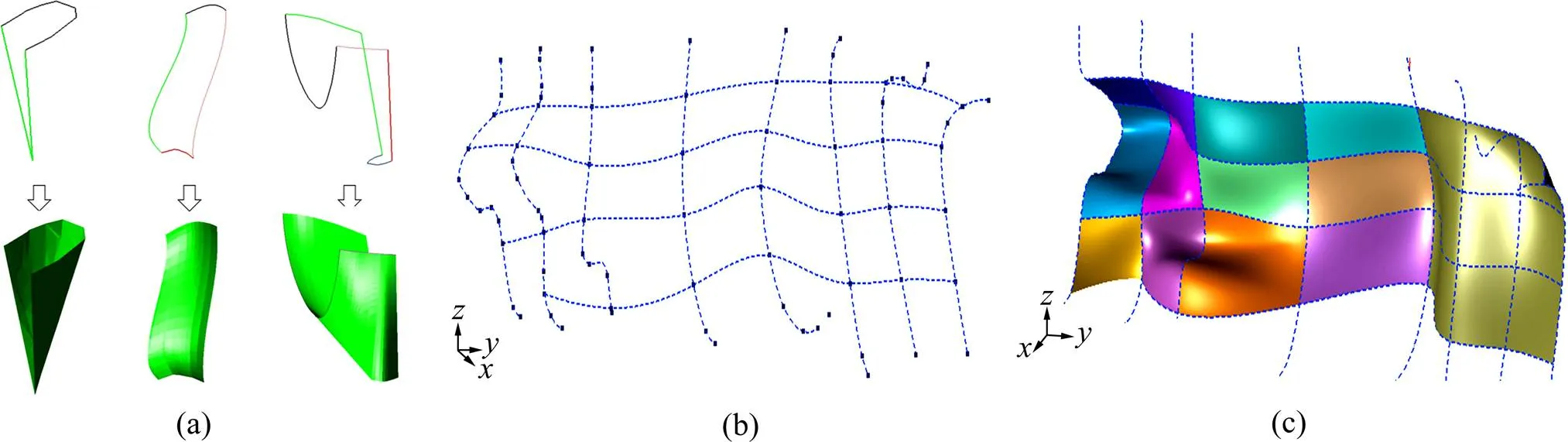
图15 基于网格的矿体模型更新[26]

3 开采规划与优化

3.1 开采单元优化布置

开采单元是指矿床开采方案优化时，将矿床在空间上按垂直方向和水平方向划分成离散的单元。从几何层面上，开采单元是按一定的尺寸粒度在空间上对矿床的离散化；从属性层面上，开采单元承载着矿岩性质、矿量、岩量、品位、开采价值和成本等信息；从经济层面上，开采单元是矿山开采进行规划和优化的基本单元。

地下开采过程中开采单元布置的合理与否，不仅影响着矿山生产系统的合理性，还影响着矿山生产规模、贫化损失指标、采矿效率等方面的效益。对开采单元进行优化布置，以实现资源有效利用、提高经济效益的过程。刘佳等[27]提出的地下采场布置优化的实现步骤如下：

1) 地下采场布置优化设计基础数据的准备，包含矿体模型、品位模型，它们主要用于计算经济技术指标参数；

2) 确定矿体走向、倾向等参数；

3) 定义地下采场布置优化设计的开采水平和分段高度信息，设置最小开采单元的尺寸；

4) 定义采矿单元布置的起始基准点，根据自定义的采矿单元详细参数快速布置，根据划分情况自动快速生成采矿单元布置图，如图16所示；

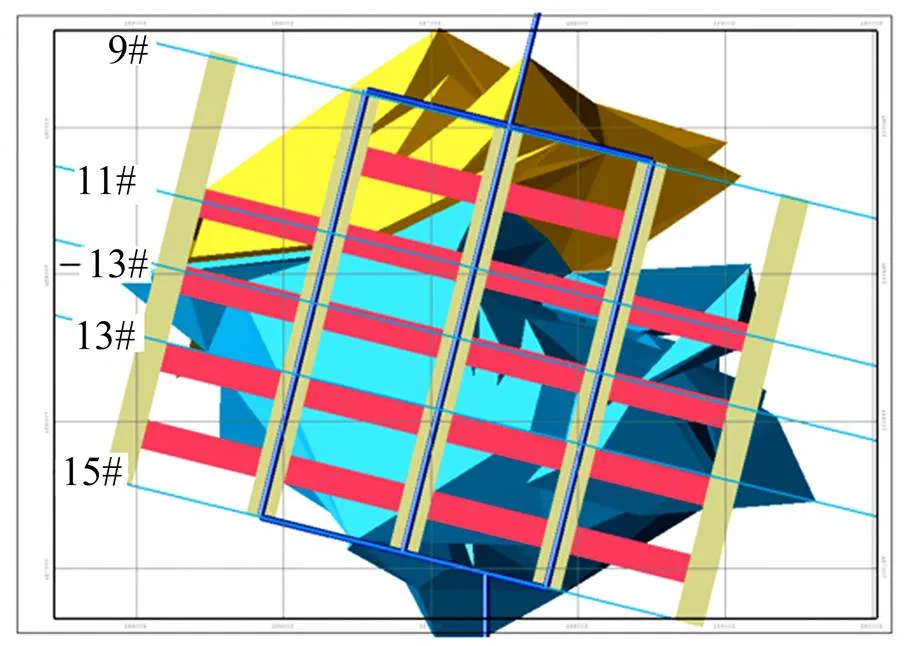
图16 开采单元布置

5) 根据采矿单元布置情况，快速建立矿房、矿柱三维实体模型，在生成采矿单元三维模型过程中，使用块段模型进行矿石量、金属量、岩石量和出矿品位等指标计算，并将结果存储到模型属性中；

6) 以初始基准点作为起始点，以指定的步距为单位向主轴或次轴方向偏移形成多个采矿单元布置方案；

7) 拟合形成各种方案的经济效益趋势，根据趋势选择出最佳采场布置方案，如图17所示。

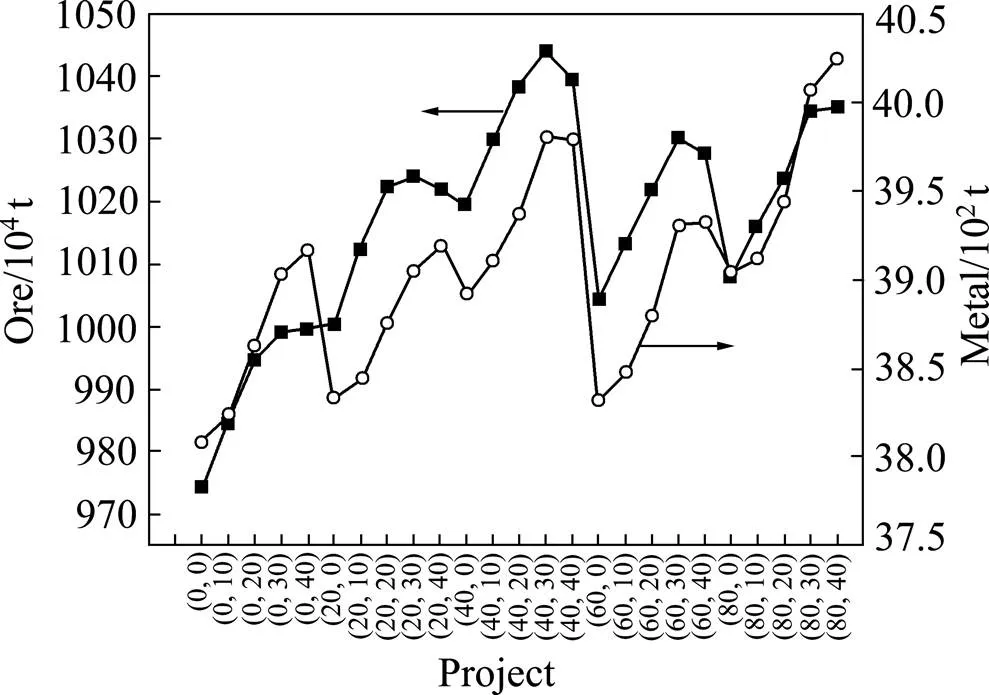
图17 开采方案经济效益趋势

3.2 境界优化

境界优化指在露天矿山实体模型、块体模型和相应经济参数的基础上、运用运筹学理论或最优化方法方法进行最终境界优选的过程。由于露天开采的对象是复杂多变的地质岩体、无序的品位分布及多变的经济参数等一系列非线性动态问题，从而提出露天境界优化理论。露天境界优化方法主要包括：浮动圆锥法、动态规划法、LG图论法和网络最大流法等。

1951年，BELLMAN等[28]提出解决多阶段决策问题的动态规划理论和方法；20世纪60年代起，动态规划广泛应用于矿山系统工程。动态规划确定最优开采境界的思路为：将露天矿分割为许多开采块段，然后将每个开采块段视为决策过程的阶段，进行多阶段决策；在决策序列中求的总盈利最大的最优策略，即最优开采境界。

LG图论法是LERCHS和GROSSMAN最初在1965年提出的[29]，是具有严格数学逻辑的最终境界优化方法，从露天开采的角度，构成一个可行的开采境界需满足几何约束条件，即从被开采节点出发引出的弧的所有节点也属于被开采之列。形成可行的开采境界的子图称为可行子图，也称为闭包。以闭包内任一节点为始点的所有弧的终点节点也在闭包内。最大闭包是具有最大开采价值的开采境界，因此求最优开采境界实质上就是在价值模型所对应的图中求最大闭包，如图18所示。

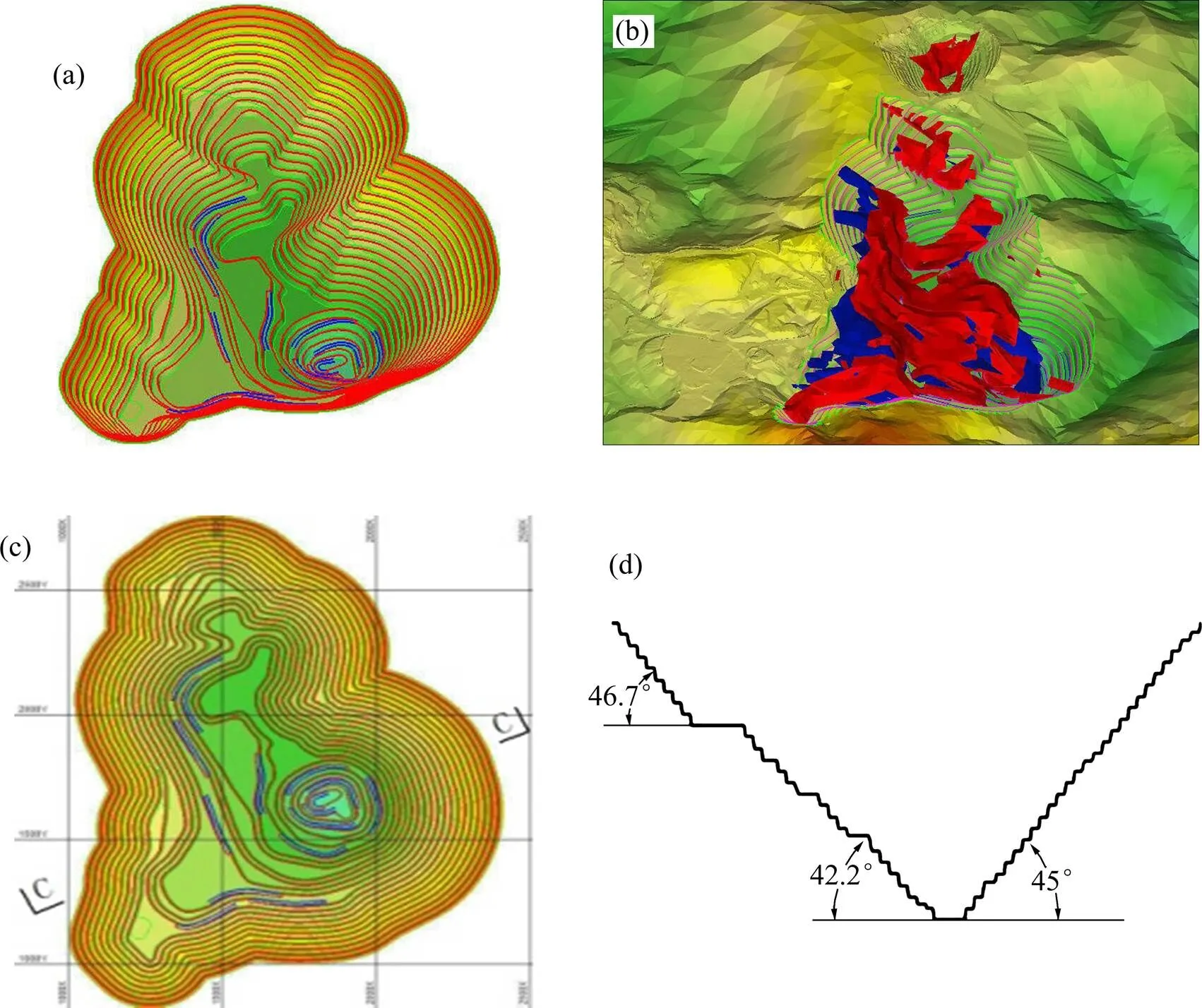
图18 LG图论法露天境界优化

1956年，FORD和FULKERSON指出最大流的流值等于最小割集的容量，并根据这一原理设计了用标号法求最大流的方法[30]；20世纪60年代以来，网络最大流方法开始应用于露天最优境界圈定。使用网络最大流法求解最优开采境界的方法为：根据矿床经济模型将露天矿离散为矿岩块段模型；构建矿岩网络图，利用网络最大流算法寻找盈利最大的块段组合，即最优开采境界。

上述境界优化算法均属于静态经济计算方法，未能考虑价值的时间因素，其结果在实际应用中未必能使企业获得最大利润，且企业无法对其投资的风险进行有效评估，在境界优化的过程中考虑价值的时间因素，对影响境界优化的各因素进行敏感性分析等，以确定最经济合理的露天境界，如图19所示[31]。在实际应用中考虑时间因素的动态方法较静态方法更具适用性。

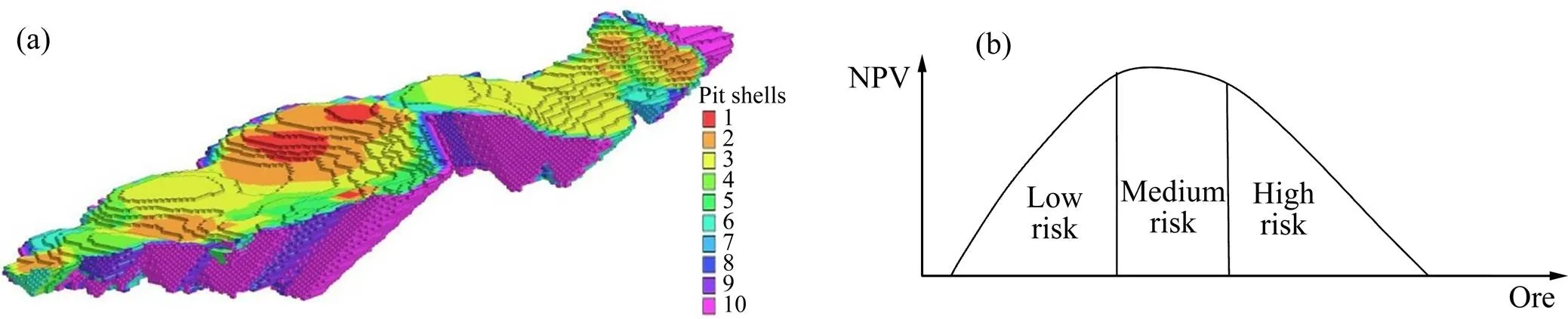
图19 最优境界敏感性分析[31]

3.3 矿山中长期计划

矿山开采中长期计划是指确定一个技术上可行，能够使矿床开采的总体经济效益达到最大的，贯穿整个矿山开采周期的开采顺序。露天采剥计划优化方法主要包括地质最优开采体序列法和运筹学方法。地质最优采场序列的生成采用浮锥排除法，构造一个锥面倾角等于工作帮坡角的正锥体，将锥顶点置于经济块段模型最底层上，计算锥体的总体积、金属量、剥离量和剥采比，如果总体积小于或等于预先设定的境界增量Δ，则将锥体按照剥采比从大到小的顺序放入一个锥体数组中，否则不做任何处理；将锥顶点移至上一层，重复上述处理，直至考虑完经济块段模型的所有层，就得到一个锥体序列数组。从该数组中选出满足锥体联合体总体积接近或者等于境界增量Δ的前个锥体，删除这些锥体，将受锥体影响的经济块段模型的底部标高提升到锥面最高的标高处，得到的一个新的采场体积比上一个采场小Δ。重复上述方法，直至得到的新的采场体积等于或者接近预先设定的最小采场，就得到了一个满足要求的地质最优开采序列，如图20所示[32]。

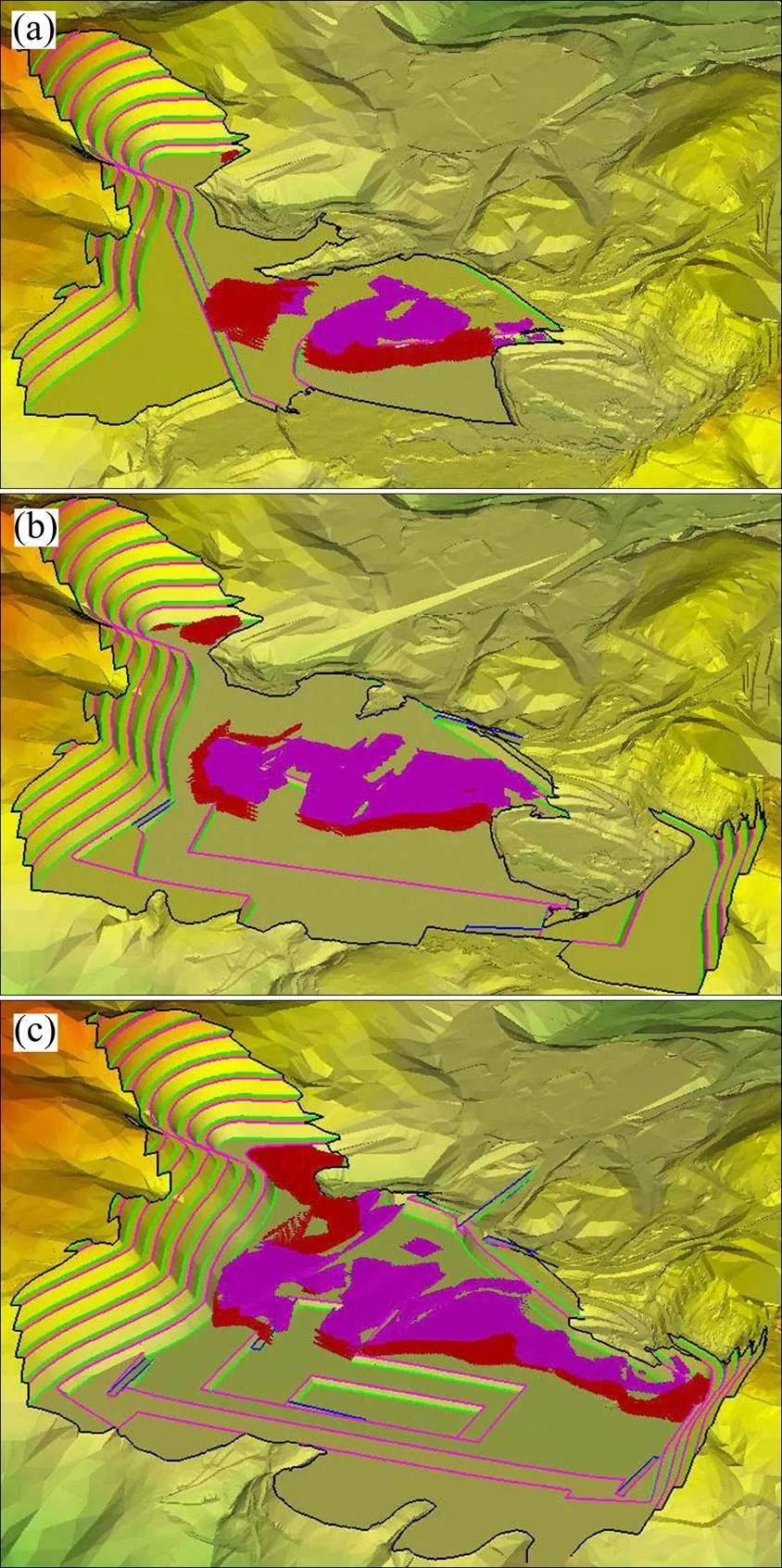
图20 露天矿生产计划优化[32]

运筹学方法主要是运用线性规划法建立露天采剥计划优化数学模型，从而求解得到最优计划。运筹学方法[33−34]也是地下矿采掘计划优化的主要方法，中长期计划优化数学模型内容包括：1) 集合，主要包括经济块段的集合和开采周期的集合；2) 参数，包括在时期开采矿块的经济价值、矿块中所包含的矿石量和周期时的开采能力范围等；3) 决策变量，即若矿块在周期时被开采，则取值为1；否则取值为0；4) 目标函数，即实现矿山开采的净现值最大化；5) 约束条件，主要包括空间位置约束、生产能力约束和选场处理能力约束等。

3.4 矿山开采短期计划

短期计划通常指编制月、周或日计划，其中配矿计划是短期计划中研究的核心问题，随着市场竞争加剧，矿山已由粗放式生产管理向精细化生产管理模式转变，传统的配矿模式远远不能满足矿山的需求。为了提高配矿效率，运筹学优化的思想开始广泛运用于配矿研究中来。王克让等[35]提出了基于0−1整数规划的配矿优化模型，以实现对各矿点矿堆的整体取舍，简化配矿和运输的管理；杨珊等[36]建立了堆积型铝土矿的配矿LP数学模型，并引入了运筹学优化软件Xpress-MP对数学优化模型求解，能较快速得到配矿结果；GU等[37]根据抛掷爆破下各排炮孔矿岩的覆盖规律，建立了爆堆品位分布的预测模型，以此为基础结合配矿优化模型，计算出电铲的作业点和产量，上述各方法在实际配矿生产中，均存在不适用性，主要原因在于将各爆堆或出矿点看作品位均匀的优化对象，对爆堆内矿石品位难以精确预知，难以保证配矿结果的准确性，此外，当选厂品位要求比较苛刻时，而实际参与供矿爆堆品位达不到标准时，数学模型难以收敛，得不到近优的配矿方案，HUANG等[38]提出了一种基于目标规划的自动化配矿方案，将爆堆划分成若干个离散单元块，然后根据炮孔岩粉数据进行地质统计学估值，然后以品位波动最小为目标函数，建立基于目标规划的露天矿配矿优化数学模型求解，配矿效果如图21和表1所示。

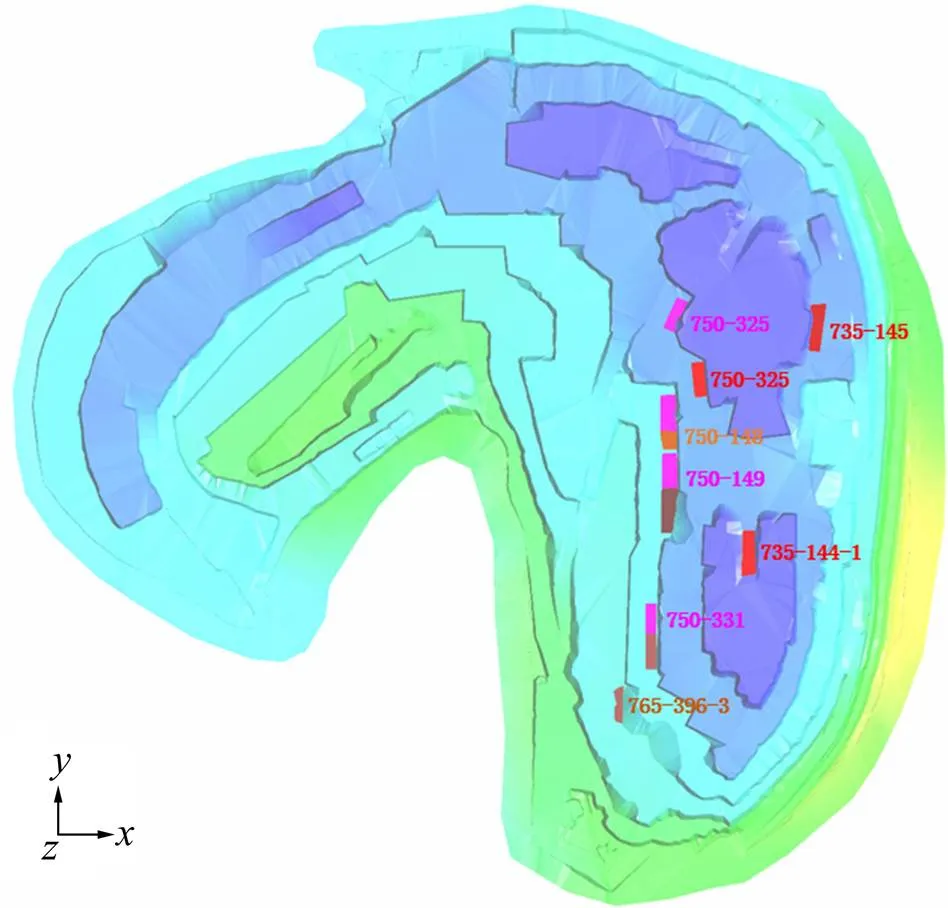
图21 自动化配矿效果

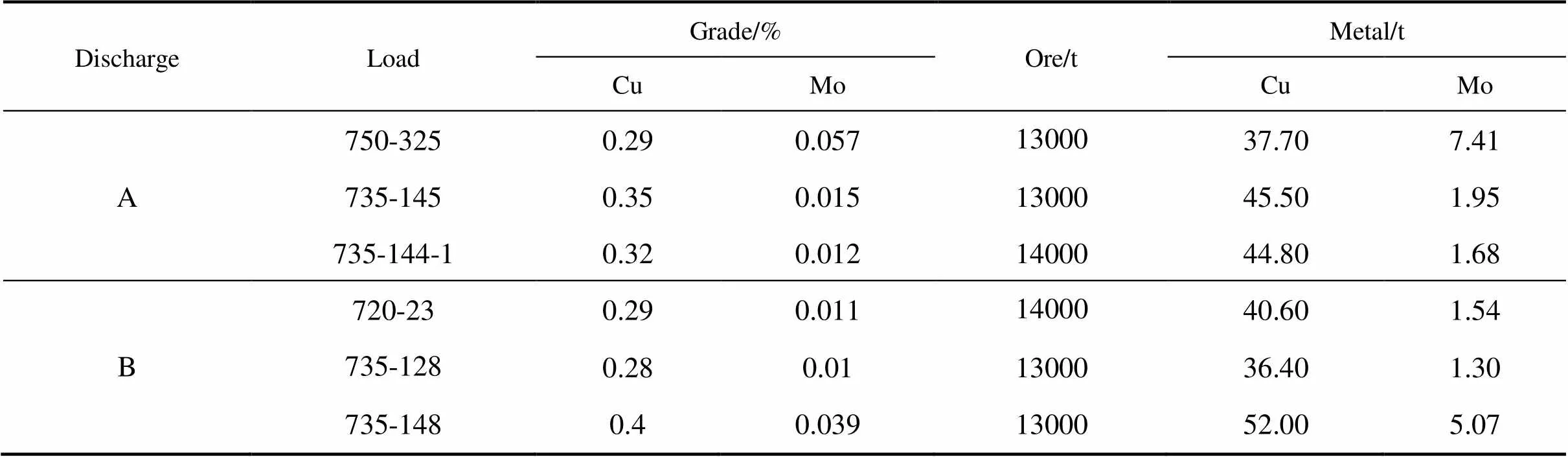
表1 自动配矿结果

4 数字化采矿设计

4.1 损失贫化控制

矿床开采始终伴随着损失贫化，尤其是工程进行至矿岩分界处，损失贫化对矿山的经济效益影响较大，主要体现在露天台阶爆破设计矿岩分界处的后冲线位置确定和地下进路炮排设计矿岩分界处的首排炮位置确定，两者原理基本类似。

露天台阶爆破设计中，在矿岩分界处通常采用分爆分采的方式，在矿体一侧布置炮孔时，需要先确定爆破后冲线的位置，然后根据后冲距离确定最后一排炮孔的位置，因此爆破后冲线位置的设定直接关系到爆破设计的损失率和贫化率，从而影响着矿山的经济效益。在露天爆破中，根据爆破后冲线位置和爆破漏斗原理，产生的爆破缓冲面是一个具有一定倾角的斜面，结合矿体边界的空间形态，分析出爆破损失的矿石和混入的废石情况，如图22所示。在此基础上计算损失率和贫化率，并判断爆破后冲线在该位置时是否满足损失贫化要求，若不满足，调整爆破后冲线位置重新计算，直至满足要求。因此矿岩分界处爆破后冲线位置的确定是个非常复杂的过程。

图22 矿岩交界面与爆破缓冲面不同空间位置类型

为实现三维空间下的损失贫化计算，建立露天坑及矿体三维模型。在矿岩交界处的爆破区域内布置炮孔设计时，需要进行损失贫化控制。李金玲等[39]提出露天台阶爆破矿岩交界处损失贫化控制系统，爆破后冲线初始位置及采样集如图23所示；三维空间中计算各采样位置下的损失贫化如图24和25所示。在此基础上，对爆破后冲线位置及其相应的指标进行最小二乘法拟合，根据损失贫化变化趋势及爆破设计要求决策最佳爆破后冲线位置。

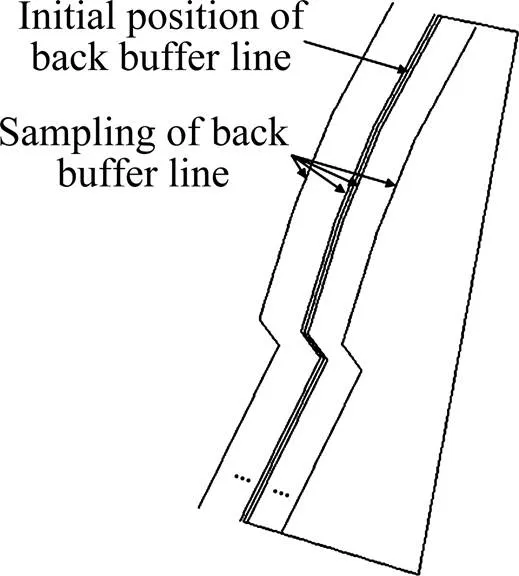
图23 爆破后冲线初始位置

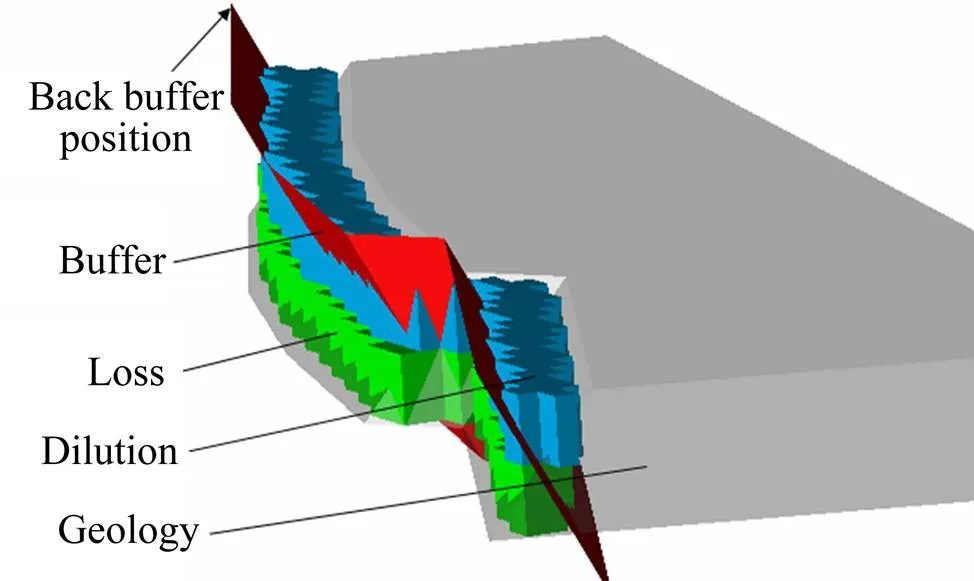
图24 矿岩交界处爆破设计损失贫化

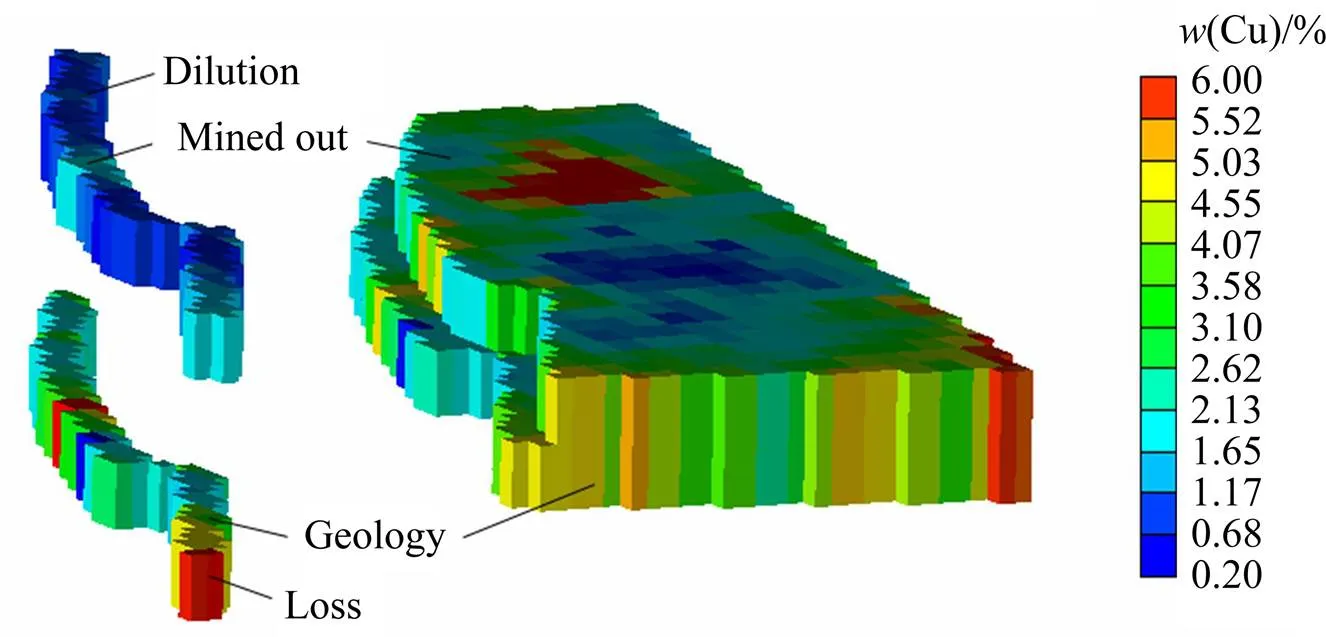
图25 动用地质矿石及采出矿石品位分布

4.2 开采设计

数字化开采设计以矿床地学数字化模型为基础、三维可视化软件为工具、计算机模拟为手段、安全高效低成本实现资源的开采为目标，进行矿山开采系统优化设计的过程。地下矿山数字化开采设计主要内容有：井巷工程设计、单体设计和回采爆破设计；露天矿山数字化开采设计主要包括以下4个方面：露天开采境界设计、露天开拓设计和穿孔爆破设计等，效果如图26所示[9]。

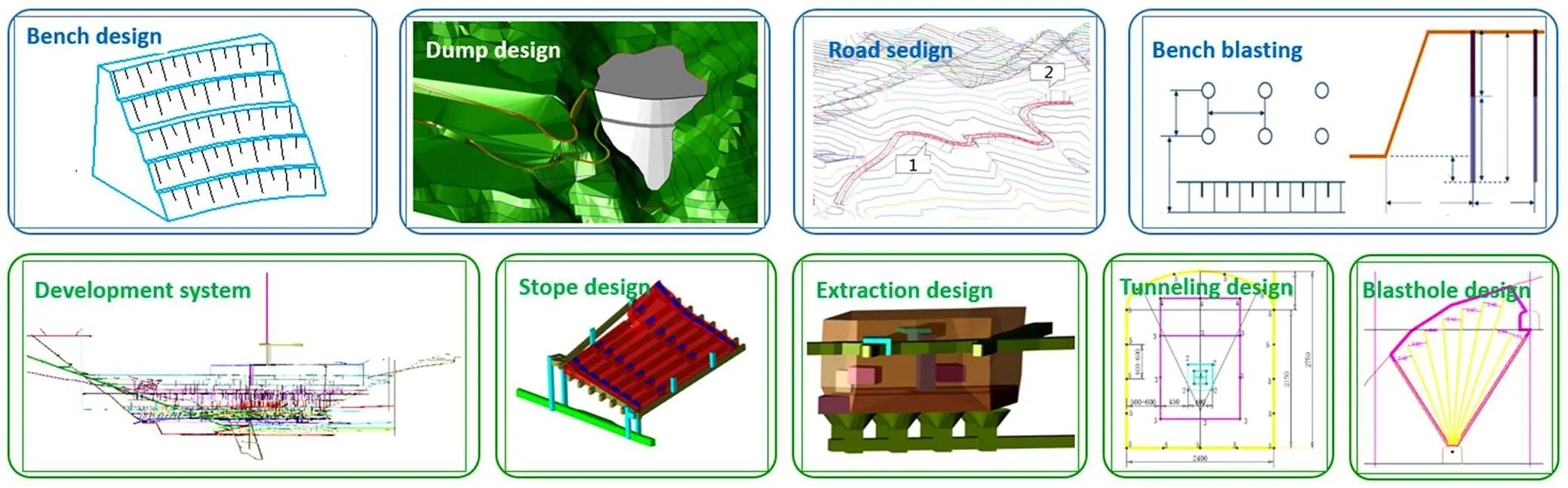
图26 数字化开采设计效果图[10]

矿山开采设计是一个充分发挥专家经验和主观能动性的创造性活动。数字化是将许多复杂多变的信息转变为可以度量的数字、数据，建立起适当的数字化模型，进行统一处理的客观而具有科学性的过 程。数字化开采设计是两者的融合与统一，是采矿技术、计算机技术、网络技术与管理科学的交叉、融 合、发展与应用的结果，与传统设计模式相比，其在过程、方法、效率和效果等方面将发生巨大的改变和提高。

5 生产管理与安全管控

5.1 按需通风与调控

通风网络解算是指根据建立的通风网络模型及其基础参数，模拟计算风量分配情况以及主要通风机工况点的过程，其实质是求解一组大型非线性方程组的解。通风网络解算可分为自然分风解算和按需分风解算。矿井通风研究时一般将复杂的矿井通风系统抽象为通风网络，对通风网络进行分析可以揭示网络内部各种内在关联关系，为网络设计和网络优化提供理论基础。网络解算的基本原理都必须遵循风流流动的三个基本定律：风量平衡定律、风压平衡定律和矿井通风阻力定律。通风网络解算作为矿井通风网络最核心的理论，一直受到通风研究工作者的普遍关注。以模拟法、试算法、解析法、图解法、等效法和渐近法(数值法)等为代表，其中尤以渐近法为代表的数值模拟方法为最重要的通风网络解算方法。

目前通风网络解算采用数值法[40]比较多，尤其是牛顿法、节点风压法、Scot-Hinsley法、线性代换法等几种方法，它们又可归纳为三类：迭代法、斜量法和直接代入法。其中Scot-Hinsley法属于迭代法；拟牛顿法是近似的牛顿法，采用一阶导数来近似牛顿法的二阶导数，属于斜量法；平均风量逼近法则属于直接代入法。各种解算方法之间既有联系又有区别，其区别主要体现在两方面，一是选取的基本未知量不同；二是求解非线性方程组的迭代计算方法不同。回路风量解算法和节点风压解算法分别是风量法和风压法这两大类算法中的代表，结算结果如图27所示[41]。

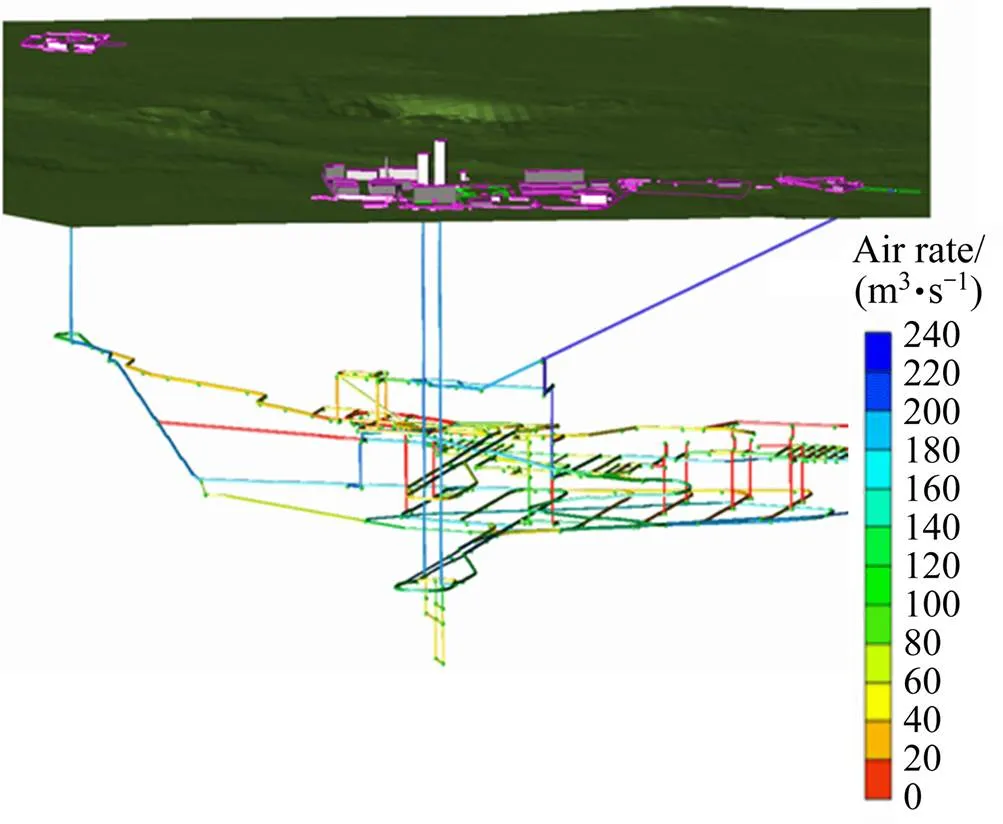
图27 三维通风网络解算[41]

为了满足采、掘工作面和硐室等需风地点需风量，通过增减通风构筑物、调节风机运转参数等措施调节风量分配情况，实现矿井按需分风的手段。具体调节方式包括风窗调节、风门调节和风机调节等。当自然分配风量小于需风量时，对该分支或其串联分支进行降阻或增压调节，或对该分支的并联分支进行增阻调节；相反，当自然分配风量大于需风量时，则在该分支及其串联分支上进行增阻调节，或在其并联分支上进行降阻或增压调节。

通风网络调节方法[42]分为定流法调节、回路法调节和通路法调节，以及非线性规划等方法。从宏观的角度看，定流法调节直接在设置固定风量的分支上进行调节，具有很多的局限性；回路法主要是局部回路中的调节，实现矿井按需分风，从而无法控制其对其他通风网络以及整个通风网络的影响；通路法则是从通风网络全局的角度出发，可根据通风巷道的客观条件和能耗情况，选择合适的调节点位置与调节点数量进行调节。

5.2 虚拟管控

虚拟管控是指以矿山安全、高效生产为目标，通过地理信息系统、虚拟现实技术以及物联网等技术，对矿山安全六大系统、通风系统、排水系统、称重计量系统等系统的数据实时接入，在此基础上进行可视化展示、查询分析、预警决策、培训演练等应用，从而实现透明、集中的可视化管控。

矿山生产可视化管控系统目标包括[43]：

1) 实现地下矿山的三维可视化。地下矿开采环境危险恶劣，生产系统多，通过信息化技术提高安全生产的水平是矿山的必由之路。安全管理的基础是对井下现场情况的了解，包括环境状况、设备工况、人员工作地点等等信息，这些也是调度指挥和生产管理的基础，只有清楚掌握井下情况了，才能有效的预防事故、指挥生产，即“可视才能可控”。

2) 高度集成的虚拟开采环境及模型为安全生产、调度决策提供基础信息服务。矿山开采是人类在复杂环境进行的复杂生产活动。生产的空间环境、生产设备、生产的规则和管理措施都有其独特之处。随着矿山调度管理工作信息化水平的提高，各种辅助决策功能将为管理者所需要，其中大部分功能都将要利用基于空间数据模型的空间分析功能。

3) 实现可视化管控系统与实际矿山的信息同步。作为“人工矿山系统”的可视化管控系统，它管理的所有对象要与实际矿山保持一致，通过它能查询矿山开采状况、生产状态和人员设备信息。同时，利用可视化管控系统辅助制定调度指挥策略，通过各种通讯手段下达命令或者报警信息，调节实际矿山系统内的生产活动。

在此技术构架上的露天矿卡车调度系统和地下矿安全避险六大系统应用效果如图28和29所示[44]。

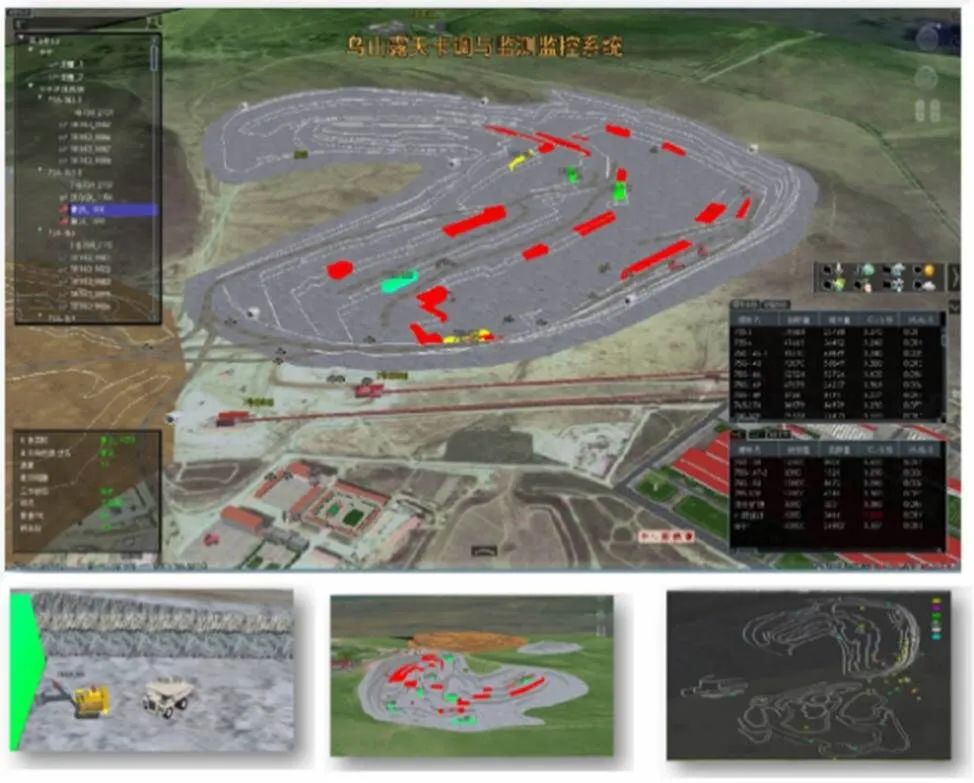
图28 三维露天矿山卡车调度系统[44]

图29 三维地下矿山生产安全监控系统[44]

5.3 生产执行

生产执行是指以生产计划为依据，采集和收集采矿、选矿、冶炼生产过程的实时工艺信息和设备运行状态信息，提供计划执行与修正、资源合理利用、产量与质量统计分析、平衡工况的优化调度、异常工况的动态调度、辅助生产调度决策等一体化解决方案的信息化系统。

生产制造执行系统[45]是美国AMR公司在20世纪90年代初提出，使用了MES概念，AMR倡导用三层模型表示制造业信息化，逐步形成两库(实时数据库、关系数据库)、三层(ERP、MES、PCS)的体系结构，MES是位于上层的计划管理系统与工业控制系统之间的面向车间层的管理信息系统。MES系统已在石化、化工、食品、制药、炼钢、造纸等行业得到了广泛的实施与应用，并逐步应用到矿山企业。

矿山生产执行系统是以采掘计划、技术经济指标计划为线索管理采矿、选矿、冶炼、质检、调度等矿山生产的原始数据，实现设备工况、材料能源、安全环保、计质量、生产调度、现场作业、生产统计与分析的协同管理，并实时监管DCS生产监控系统的生产工艺信息和设备运行状态信息，经过分析处理，形成管理中需要的各种报表及分析结果。

生产执行系统贯穿于整个矿山生产的全过程，做到“实时监控、平衡协调、动态调度、资源优化”，从而最大化的规避安全风险，挖掘设备的生产潜力，降低生产成本，改善企业生产状况，持续提高生产力和劳动生产率，实现精益生产，为企业的生产组织和管理工作带来全面提升、增添新的价值。

5.4 智能调度

采矿生产过程的各种参数，如设备的工况、状态、采场的道路情况、天气情况、矿石废石的性质等因素，都对生产效率的发挥，及生产目标的实现起着制约作用，如何在众多的约束下，取得最高的设备作业效率，就需要每时每刻实时地对整个参加生产的设备的搭配进行调整，使之最大限度地发挥作用，提高整个采矿作业的台时效率，这就是一个动态控制过程，实际应用中的主要包括露天卡车调度和地下矿列车运行调度。

实时调度[46]是卡车调度的核心问题，它是在车流规划的基础上，针对露天矿当前作业状态变化，对收到的卡车分派请求，进行实时优化调度决策，将最佳卡车分配到最需车的电铲线路上去。从而以最高的设备作业效率，实现计划生产目标，卡车调度系统如图30所示。国内外许多专家学者作了大量的研究工作，提出了一些实时调度准则和方法。按照优化调度准则所追求的目标不同，可将现有的实时调度划分为两大基本类型：第一类主要以提高电铲、卡车的效率从而提高全矿产量为主要目标。主要包括最早装车法、最大卡车法、最大电铲法、最小饱和度法。第二类实时调度准则所追求的目标是尽可能实现货流规划的结果为主要目标，主要有两阶段算法、最小比值方差算法、比率法等。

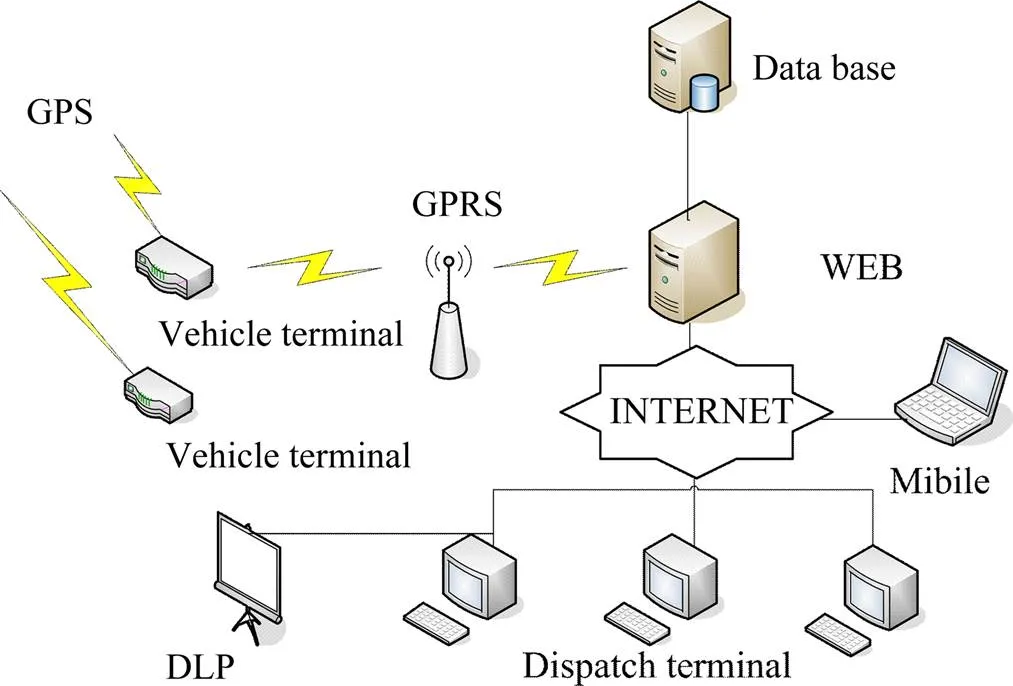
图30 卡车调度系统图示

运行图[47]是地下矿轨道运输计划编制和行车组织安排的基础，规定了机车不同时刻在区间的位置、在装载点的装载作业时间、在卸载点的卸载作业时间、在节点的等待时间以及在区间的运行时间和机车的交路情况。机车运行图实质上是矿山企业进行运输工作的生产计划，它规定了每辆机车需要前往的装载点以及卸载点。地下矿运输的过程相当复杂，需要轨道、道岔、信号、供电、通讯以及监控等各部分相互配合；机车运行图详细标明了机车前往的装载点、卸载点、以及运行路径、时刻、次数，如图31所示，为人工编制运输计划提供了一定的依据，也为企业从事运输工作的管理者节约了大量的编制机车运输计划的时间；对指导矿山实际运输工作具有重要的现实意义。

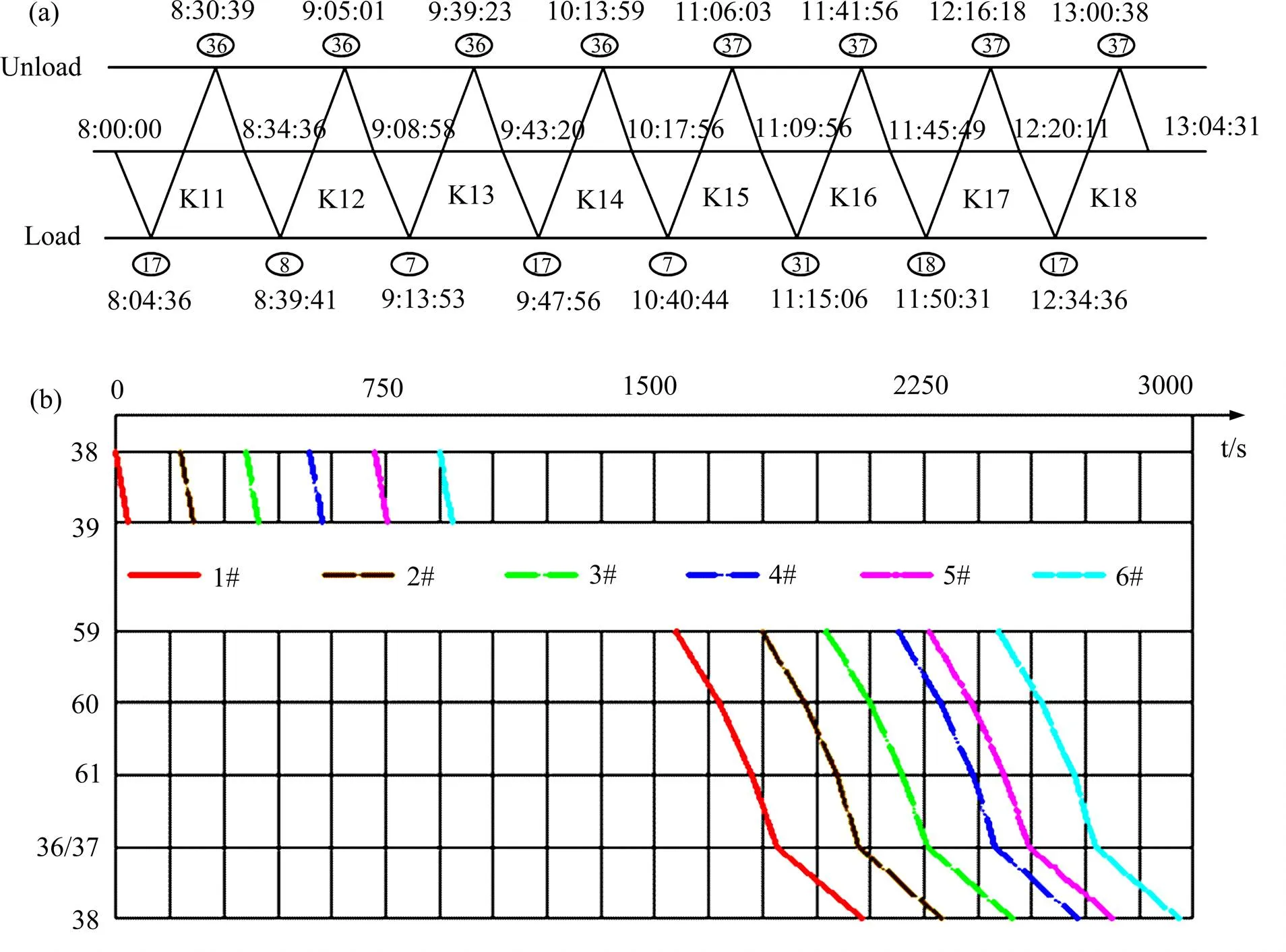
图31 地下矿列车运行图

6 结语

矿业是一个古老而具有传统的行业，观念的革新是行业进步的基础。随着国家经济结构的深度调整，矿业行业所面临的“低增长、低效益、低价格和高压力”将成为未来一段时期的新常态，也使其生存和发展面临挑战。从长远的角度来看，只有在理念、商业模式、管理、技术等方面实现转型与创新，才能使矿山企业走出困局。最近国家连续推出的“中国制造2025”、“互联网+”和“一带一路”等新政策为矿山企业转型提供了强大的政策支持，信息技术和制造技术的快速发展，为矿山企业加速技术革新提供技术保障，给矿山企业创新发展带来了前所未有的机遇。

无论再过多长时间，我们拥有的资源条件都不会发生根本性的变化，而市场和需求却永远在变。当市场价格高涨时，无论采用何种工具和技术，企业都可能盈利，这时技术看上去只是锦上添花。而当市场价格低迷时，我们即使竭尽全力也常常会在盈亏平衡点附近徘徊，这时只有创新的技术才能给我们雪中送炭。加工制造业可以通过不断地创新和新产品开发来平衡市场价格的变化对企业效益的影响，而矿山企业只能通过生产工具的进步和技术与管理模式的创新来提高生产效率、降低生产成本、减小价格波动对企业经济效益带来的影响。尽管目前我国的数字矿山技术还不能彻底解决矿山企业所面临的困境，但行业的共同努力一定会缩短矿山企业摆脱困境、迈向成功的时间。

REFERENCES

[1] TRUDEL B, NADEAU S, ZARAS K, DESCHAMPS I. Managing equipment innovations in mining: A review[J]. Work, 2015, 51(4): 731−746.

[2] 吴立新, 殷作如, 钟亚平. 再论数字矿山: 特征、框架与关键技术[J]. 煤炭学报, 2003, 28(1): 1−7. WU Li-xin, YIN Zuo-ru, ZHONG Ya-ping. Restudy on digital mine: characteristics, frame work and key technologies[J]. Journal of China Coal, 2003, 28(1): 1−7.

[3] Darling, Peter. SME mining engineering handbook[M]. Englewood, Colo: Society for Mining, Metallurgy, and Exploration, 2011, 0−1840.

[4] JONATHAN R S, BRIELIN C B. Fast segment insertion and incremental construction of constrained Delaunay triangulations [J]. Computational Geometry, 2015, 48(8): 554−574.

[5] PAUL M, JU J Z. Triangle refinement in a constrained Delaunay triangulation skeleton[J]. Pattern Recognition, 2007, 40(10): 2754−2765.

[6] JOACHIM G, HERMAN J H, MARC V K. Constrained higher order Delaunay triangulations[J]. Computational Geometry, 2015, 30(3): 271−277.

[7] 毕 林, 王李管, 陈建宏, 徐志强. 基于CDT与布尔运算的露天矿三维建模[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(4): 529−532. BI Lin, WANG Li-guan, CHEN Jian-hong, XU Zhi-qiang. A 3D model of surface mine based on CDT and Boolean operation[J]. Journal of Liaoning Technical University (Natural Science), 2009, 28(4): 529−532.

[8] 陈学工, 黄 伟, 季 兴, 李 楠. 一种由轮廓线重建物体表面的方法[J]. 计算机工程与应用, 2011, 47(14): 157−159. CHEN Xue-gong, HUANG Wei, JI Xing, LI Nan. Solution to surface reconstruction from contours[J]. Computer Engineering and Applications, 2011, 47(14): 157−159.

[9] GLANZING M, MALIK M M, GROLLER M E. Locally adaptive marching cubes through iso-value variation[C]// Proceedings of 17th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Tschechien: Eurographics Association, 2009: 33−40.

[10] 毕 林. 数字采矿软件平台关键技术研究[D]. 长沙: 中南大学, 2010. BI Lin. Study of key technology of platform of digital mining software system[D]. Changsha: Central South University, 2010.

[11] CONGOTE J, MORENO A, BARANDIARAN I. Extending marching cubes with adaptative methods to obtain more accurate iso-surfaces[J]. Communications in Computer and Information Science, 2010, 68(1): 35−44.

[12] CIGNONI P, GANOVELLI F, MONTANI F, SCOPIGNO F. Reconstruction of topologically correct and adaptive trilinear isosurfaces[J]. Computers & Graphics, 2000, 24(3): 399−418.

[13] NIELSON G M. On marching cubes[J]. IEEE Transactions on Visualization and Computer Graphics, 2003, 9(3): 283−297.

[14] 杨鸿翼, 刘亮明, 赵义来. 基于Kriging和Marching cube算法的地学3维形态模拟[J]. 中国图象图形学报, 2008, 13(3): 531−535. YANG Hong-yi, LIU Liang-ming, ZHAO Yi-lai. 3D geological modelling based on Kriging and Marching cube algorithm[J]. Journal of Image & Graphics, 2008, 13(3): 531−535.

[15] HOPPE H, DEROSE T, DUCHAMP T. Surface reconstruction from unorganized points[C]// Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH. Chicago:Chemical Rubber Company Press, 1992: 71−78.

[16] DAVID C S. A greedy Delaunay based surface reconstruction algorithm[J]. The Visual Computer, 2004, 20(1): 4−16.

[17] GRAZIELA G, MICHAEL M H. Surface reconstruction using Delaunay triangulation for applications in life sciences[J]. Computer Physics Communications, 2011, 182(4): 967−977.

[18] 郑顺义, 苏国中, 张祖勋. 三维点集的自动表面重构算法[J]. 武汉大学学报(信息科学版), 2005, 20(2): 154−157. ZHANG Shun-yi, SU Guo-zhong, ZHANG Zu-xun. Automatic reconstruction of 3D surface model with 3D irregular points based on projection constrain[J]. Geomatics and Information Science of Wuhan University, 2005, 20(2): 154−157.

[19] 张 帆, 黄先锋, 李德仁. 基于球面投影的单站地面激光扫描点云构网方法[J]. 测绘学报, 2009, 38(1): 48−54. ZHANG Fan, HUANG Xian-feng, LI De-ren. Spherical projection based triangulation for one station terrestrial laser scanning point cloud[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 48−54.

[20] 陈 鑫, 王李管. 矿山采空区单站激光等距扫描与高效三维重建方法[J].中国矿业大学学报, 2016, 45(4): 1−7. CHEN Xin, WANG Li-guan. 3D laser equidistant scanning method from single station and efficient modeling algorithm for mine goaf[J]. Journal of China University of Mining & Technology, 2016, 45(4): 1−7.

[21] 荆永滨, 王李管, 毕 林, 陈建宏. 复杂矿体的块段模型建模算法[J]. 华中科技大学学报(自然科学版), 2010, 38(2): 97−100. JING Yong-bin, WANG Li-guan, BI Lin, CHEN Jian-hong. Robust creation of block model from complex orebody model[J]. Journal of Huazhong University of Science & Technology, 2010, 38(2): 97−100.

[22] 毕 林, 王李管, 陈建宏, 冯兴隆. 基于八叉树的复杂地质体块段模型建模技术[J]. 中国矿业大学学报, 2008, 37(4): 532−537. BI Lin, WANG Li-guan, CHEN Jian-hong, FENG Xing-long. Study of octree-based block model of complex geological bodies[J]. Journal of China University of Mining & Technology, 2008, 37(4): 532−537.

[23] 谭正华. 三维可视化环境下采矿设计与生产规划关键技术研究[D]. 长沙: 中南大学, 2010. TAN Zheng-hua. Study on key technology of mining design and production planning based on 3D visualization system[D]. Changsha: Central South University, 2010.

[24] 谭正华, 王李管, 熊书敏, 刘任任. 基于实测边界线的地下巷道三维建模方法[J].中南大学学报(自然科学版), 2012, 43(2): 626−631. TAN Zheng-hua, WANG Li-guan, XIONG Shu-min, LIU Ren-ren. 3D modeling method for laneway entities based on measured boundary lines[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 626−631.

[25] 谭正华, 王李管, 毕 林, 陈建宏. 平面连通巷道三维实体分层建模方法[J]. 武汉大学学报(信息科学版), 2010, 35(3): 360−364. TAN Zheng-hua, WANG Li-guan, BI Lin, CHEN Jian-hong. A hierarchical modeling method for plane connected three-dimensional laneway entity based on media curves[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 360−364.

[26] 杨 洋, 潘 懋, 吴耕宇, 孙 颖, 李魁星. 一种新的轮廓线三维地质表面重建方法[J]. 地球信息科学学报, 2015, 17(3):253-259. YANG Yang, PAN Mao, WU Geng-yu, SUN Ying, LI Kui-xing. High quality geological surface reconstruction from planar contours[J]. Journal of Geo-Information Science, 2015, 17(3):253−259.

[27] 刘 佳, 王李管, 朱利晴. 金属矿山采矿单元布置多方案优化设计[J]. 黄金科学技术, 2016, 24(2): 14−20. LIU Jia, WANG Li-guan, ZHU Li-qing. Optimization design of metal mine’s multi-layout program[J]. Gold Science and Technology, 2016, 24(2): 14−20.

[28] 蒋中一, 曹 乾. 动态最优化基础[M]. 北京: 中国人民大学出版社, 2015: 28−37. JIANG Zhong-yi, CAO Qian. Elements of dynamic optimization[M]. Beijing: Renmin University of China Press, 2015: 28−37.

[29] LERCHS H, GROSSMANN I F. Optimum design of open-pit mines[J]. Transactions of The Institution of Mining and Metallurgy, 1965, 68(1):17−24.

[30] 甘应爱, 田 丰, 李维铮. 运筹学[M]. 北京: 清华大学出版社, 2005: 268−276.GAN Ying-ai, TIAN Feng, LI Wei-zheng. Operations research[M]. Beijing: Tsinghua University Press, 2005: 268−276.

[31] GHOLAMNEJAD J, MOJAHEDFAR A R. Determination of the largest pit with the non-negative net profit in the open pit miners[J]. Journal of Mining and Environment, 2010, 2(1): 45−52.

[32] 黄俊歆, 郭小先, 王李管, 谭正华, 毕 林, 李 德, 陈建宏. 一种新的用于编制露天矿生产计划开采模型[J]. 中南大学学报(自然科学版), 2011, 42(9): 2819−2824. HUANG Jun-xin, GUO Xiao-xian, WANG Li-guan, TAN Zheng-hua, BI Lin, CHEN Jian-hong. A novel mining model for open-pit mine production scheduling[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2819−2824.

[33] 高永涛, 吴顺川. 露天采矿学[M]. 长沙: 中南大学出版社, 2008: 320−325. GAO Yong-tao, WU Shun-chuan. Open-pit mine engineering[M]. Changsha: Central South University Press, 2008: 320−325.

[34] ALEXANDRA M N. ENRIQUE R. RODRIGO C, ANDRÉS W. KELLY E. A review of operations research in mine planning[J]. Interfaces, 2010, 40(3): 222−245.

[35] 王克让, 陆厚华, 杜雅君. 利用0−1整数规划法进行原矿配矿[J]. 轻金属, 1997(12): 13−15. WANG Ke-rang, LU Hou-hua, DU Ya-jun. Using 0−1 integer programming for ore mine[J]. Light Metal, 1997(12): 13−15.

[36] 杨 珊, 陈建宏, 杨海洋, 刘 霁, 永学艳. 基于Xpress-MP堆积型铝土矿堆场配矿优化研究[J]. 金属矿山, 2010, 39(3): 9−11. YANG Shan, CHEN Jian-hong, YANG Hai-yang, LIU Ji, YONG Xue-yan. Optimization research of accumulated bauxite ore blending in yard based on Xpress-MP[J]. Metal Mine, 2010, 39(3): 9−11.

[37] GU Qing-hua, LU Cai-wu, LI Fa-ben, WAN Chang-yong. Dynamic management system of ore blending in an open pit mine based on GIS/GPS/GPRS[J]. Mining Science & Technology, 2010, 20(1): 132−137.

[38] HUANG Jun-xin, WANG Li-guan, XIONG Shu-min, XU Shao-you, TAN Zheng-hua, WANG Hai-qiao. Circle geometric constraint model for open-pit mine ore-matching and its applications[J]. Journal of Central South University, 2012, 19(9): 2598−2603.

[39] 李金玲, 王李管, 陈 鑫. 露天台阶爆破矿岩交界处损失贫化控制系统[J]. 黄金科学技术, 2016,24(3):14−20. LI Jin-ling, WANG Li-guan, CHEN Xin. Ore loss and dilution control system at ore-rock border for open pit bench blasting[J]. Gold Science and Technology, 2016, 24(3):14−20.

[40] CHEN K, SI J, ZHOU F B, ZHANG R W, SHAO H, ZHAO H M. Optimization of air quantity regulation in mine ventilation networks using the improved differential evolution algorithm and critical path method[J]. International Journal of Mining Science and Technology, 2015, 25(1): 79−84.

[41] 钟德云, 王李管, 毕 林, 王晋淼, 朱忠华. 基于回路风量法的复杂矿井通风网络解算算法[J]. 煤炭学报, 2015, 40(2): 365－370. ZHONG De-yun, WANG Li-guan, BI Lin, WANG Jin-miao, ZHU Zhong-hua. Algorithm of complex ventilation network solution based on circuit air-quantity method[J]. Journal of China Coal Society, 2015, 40(2): 365－370.

[42] ACUÑA, ENRIQUE I, LOWNDES, IAN S. A review of primary mine ventilation system optimization[J]. Interfaces, 2014, 44(2): 163−175.

[43] 熊书敏. 地下矿生产可视化管控系统关键技术研究[D]. 长沙:中南大学, 2012. XIONG Shu-min. Study on key technologies of underground mine production 3D visual management and control system[D]. Changsha: South Central University, 2012.

[44] 熊书敏, 王李管, 黄俊歆, 陈建宏. 地下矿可视化生产管控系统参数化数据模型[J]. 中南大学学报(自然科学版), 2012, 43(1): 272−277. XIONG Shu-min, WANG Li-guan, HUANG Jun-xin, CHEN Jian-hong. Parametric data model for underground mine 3D visual production management and control system[J]. Journal of Central South University(Science and Technology), 2012, 43(1): 272− 277.

[45] 沈清泓. 企业制造执行系统和关键性能指标评估技术研究[D]. 杭州: 浙江大学, 2013. SHEN Qing-hong. Research on manufacturing execution system and key performance indicator evaluation technology of enterprise[D]. Hangzhou: Zhejiang University, 2013.

[46] SOUZA M J F, COELHO I M, RIBAS S, SANTOS H G, MERSCHMANN L H C. A hybrid heuristic algorithm for the open-pit-mining operational planning problem[J]. European Journal of Operational Research, 2010, 207(2): 1041−1051.

[47] 谭期仁, 王李管, 钟德云. NSGA-Ⅱ算法在井下多目标运输路径优化中的应用[J]. 黄金科学技术, 2016, 24(2): 95−100. TAN Qi-ren, WANG Li-guan, ZHONG De-yun Application of NSGA-II in multi-objective route optimization of under-ground mine’s transportation[J]. Gold Science and Technology, 2016, 24(2): 95−100.

Advancing technologies for digital mine

WANG Li-guan1, 2, CHEN Xin1, 2

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. Research Center of Digital Mine, Central South University, Changsha 410083, China)

The application of "digital mine" as the national strategy of the two fusion in the mineral resources industry, influenced the new normal development of mine enterprises increasingly. Combined with the characteristic of the mining enterprise production process, the concept of digital mine was proposed. With the advancing technologies and application clues, the new technologies and development of mine resource evaluation and modeling, production planning and optimization, digital mine design, production management and safety control were introduced, and the technical innovation and application prospect of informatization and intelligentization, which provided fruitful suggestions for the future development of mining enterprises, were pointed out.

digital mine; 3D visualization; resource model; production planning and optimization; digital design; intelligent management and control

Project(2016zzts090) supported by the Fundamental Research Funds for the Central Universities of Central South University; Project(2015CX005)supported by Innovation Driven Plan of Central South University

2016-02-28; Accepted date:2016-06-25

WANG Li-guan; Tel: +86-13808478410; E-mail: liguan_wang@163.com

1004-0609(2016)-08-1693-18

P208

A

中南大学中央高校基本科研业务费专项资金资助(2016zzts090)；中南大学“创新驱动计划”项目资助(2015CX005)

2016-02-28；

2016-06-25

王李管，教授，博士；电话：13808478410；E-mail: liguan_wang@163.com

(编辑 何学锋)