PageRank 大规模实现中的存储问题研究

史倩，张家健，张伟

（1.河海大学商学院，江苏南京210000；2.江苏省邮电规划设计院有限公司江苏南京210000）

PageRank 大规模实现中的存储问题研究

史倩1，张家健2，张伟2

（1.河海大学商学院，江苏南京210000；2.江苏省邮电规划设计院有限公司江苏南京210000）

基于PageRank模型扩展到网络大小的规模时会面临诸如如何存储矩阵、PageRank的解的精度、收敛准则、悬挂节点如何处理等问题，本文通过对链接分析算法的数学内容分析，研究了PageRank部分的数学元素的存储问题、悬挂结点以及后退按钮建模的算法和优缺点，在此基础上，对压缩邻接链表信息的两种方法进行对比分析，总结出不同方法的使用条件。选择新的算法以恢复每个悬挂结点各自的评分并去除排名中的有偏性，并对后退按钮建模的回弹模型进行分析。

PageRank；存储问题；悬挂结点；后退按钮建模

PageRank模型扩展到网络大小的规模时会面临诸如如何存储矩阵、PageRank的解的精度、收敛准则、悬挂节点如何处理等问题。搜索引擎需要巨量的存储设施，以将网页及其位置、倒排索引和图像索引、内容评分、PageRank评分以及超链接图等信息加以存档。同时，开始进行PageRank的大规模实现时，必须在设计方面做出决策以确定如何处理悬挂结点问题，与悬挂结点相关的便是后退按钮的问题，这些问题得到研究者越来越多的重视，并从不同研究角度给出了有效的研究方法。

表1　PageRank问题的存储需求

1　存储问题

设计表1中的项目以计算PageRank向量，其中nnz（H）是H中的非零元素的个数，是悬挂结点的个数，而n是网络图中网页的数量。当个性化向量vT为均匀分布向量（vT= eT/n）时，其存储不需要任何空间。以平均计算，每个页面包含约10条出链，因此nnz（H）约为10 n，由此可知表1所开列的项目中，稀疏的超链接矩阵H需要最大的存储空间。

进一步分析的存储问题，对于万维网的小规模子集，当H矩阵能够被存放在主存中时，PageRank向量的计算可以用常规方式来计算。但是，当H矩阵不能被容纳在主存中时，当一个大的超链接矩阵超出了机器的内存容量时，可以采取如下方法：1）对所需的数据进行压缩，使得数据的压缩表达能够被容纳在主存中，然后实现一个应用于压缩表达上的PageRank的改进版本；2）保持数据的未压缩形式不变，进而专门针对大规模未压缩数据计算的高效实现开发出I/O。当超链接矩阵H是中等网络规模并且能够被容纳在主存时，1）对于随机上网者模型，H矩阵可以被分解为对应于结点出度的对角阵D的逆与元素值为0或1的邻接矩阵两者的乘积。首先，进行简单的分解H=D-1L以节约存储空间，其中，当i为非悬挂结点时［D-1］ii=1/dii，否则为0。可知，与存放nnz（H）个双精度浮点型的实数相比，可以存储n个整数和nnz（H）个整数，此时整数比双精度浮点数需要的空间更少；其次，H=D-1L减少了每次PageRank幂法迭代中的计算量，此时的幂法迭代以如下方式进行：

其中，计算量最大的部分是向量-矩阵乘法π（k）TH，需要nnz（H）次乘法和nnz（H）次加法。利用向量diag（D-1），π（k）TH的计算可以按π（k）TD-1L=（π（k）T）.*（diag（D-1））L的方式完成，其中.*表示两个向量的逐元素乘法。第一个部分（xT）.*（diag（D-1））需要n次乘法。由于L是一个邻接矩阵，（π（k）T）.*（diag（D-1））L只需要n次乘法和nnz（H）次加法；2）对于智能上网者模型，可以使用行压缩存储或列压缩存储等其他的紧凑存储方案，需要注意的是，对于每种压缩格式，在节省了一定存储空间的同时，在进行矩阵运算时需要更多额外的计算量［1］。

PageRank模型将H或L矩阵存放于矩阵各列中的元素所对应的邻接链表中［2］，为了计算PageRank向量，PageRank幂法需要在每次迭代k中计算向量-矩阵乘法π（k）TH［3］，因此，需要加速算法以实现对矩阵H或L的列的迅速访问［4］。

压缩邻接链表信息的方法：

1）间隔法。间隔法利用了通过超链接连在一起的文档之间所具有的局域性，其中，局域性所指向的事实即通过某个超链接联系起来的原页面和目标页面，其页面序数通常是比较接近的［5］。编号100的页面常常拥有一些序数接近的入链，这些入链更可能来自页面112、113、116和117，并非来自页面924和4 931 010。由此可知，页面100对应的邻接链表中的信息可按以下方式存储，如表2。

表2　页面100对应的邻接链表

页面100的第一个入链页面的编号——即112——被保存下来，而在它之后，仅保存后续的入链页面编号与前一个页面编号之间的间隔。由于这些间隔通常都是较小的整数，因此保存它们只需要较少的存储时间。

2）压缩方法。压缩方法利用网页之间的相似性，如果页面Pi和Pj具有相似的邻接链表，那么就可以利用邻接链表Pi中的项来表示邻接链表Pj，从而达到压缩的目的此时Pi称为Pj的参考页。例如图1。

图1　邻接链表Pi对邻接链表Pj的表示

Pj页面的邻接链表与Pi的邻接链表相似，两个页面均具有指向页面5，12，101和190的出链，因此，需要构造一个有1和0构成的共享向量和一个整型的差异向量以利用该重复性。二值得共享向量的大小和Pi的邻接链表的大小相同，如果的Pi邻接链表中的第k个条目出现在了Pj的邻接链表中，则共享向量的第k个位置上的值为1；参考编码中的第二个向量则是Pj的邻接链表中没有出现Pi的邻接链表中的那些条目所构成的链表。需要指出，Pj的共享向量的存储开销将少于Pj的邻接链表，因此，压缩方法的有效性依赖于差异页面的多少。如果Pi和Pj的邻接链表中页面的重复率很高，则差异向量将很短，Pi有可能是Pj的一个有效参考页面。但是需要注意，为索引中的每个页面都确定一个参考页面的难度较高［6-7］。

2　悬挂结点算法

对于大部分的悬挂结点而言，其相似度较高，其对应的H以及S和G中的行是相似的［8］。同时，一旦随机上网者到达了一个悬挂结点，那么其行为方式总是相同的，不论其是处于哪个特定的悬挂结点，该上网者总是立即跳转到一个新的页面［9］。其中，如果vT=eT/T，即为随机跳转，如果vT≠eT/T，则根据相应的跳转概率跳转。由此可知，如果把所有单个的悬挂结点汇聚成一个新的转跳状态，将极大缩小悬挂结点问题的规模，特别是当悬挂结点所占的比例很高时。但是，当系统较小时该做法会面临新的问题：1）排名评分只能对非悬挂页面加上一个归总的跳转状态来给出；2）这个较小的排名集合是有偏的。在此本文选择新的算法以恢复每个悬挂结点各自的评分并去除排名中的有偏性［10］。

假设H的行和列的下标均被重新排序，使得对应于悬挂结点的行处在矩阵的底部。

该式中，ND是非悬挂结点的集合，而D是悬挂结点的集合。此时，稀疏线性系统形式πT（I-αH）=vT，且πT=X/XTe中的系数矩阵变为：

它的逆为：

因此，未归一化的PageRank向量的πT=vT（I-αH）-1可以写为:

该式中，个性化向量vT被相应地划分为非悬挂部分（）和悬挂部分（）。

该计算PageRank向量的算法利用了悬挂结点调整的秩一结构以及可聚性，从而可以仅使用网络中的非悬挂部分来完成计算，该算法较为简单。对于在H的子矩阵中找到更多的0T行，可以通过将定位全零行的过程递归地重复应用于H的趋于小的子矩阵之上，直至获得一个没有任何全零行的子矩阵位置。小的子系统XT1（I-αH）=vT可使用直接法或迭代大求解。该悬挂结点PageRank算法具有渐进收敛率，由于其运行于一个规模较小的问题之上，因此所需的时间少于标准的PageRank幂法。

3　后退按钮建模

与悬挂结点相关的便是后退按钮的问题。对网络浏览器上的后退按钮进行建模，可以在PageRank模型中对后退按钮进行有限度使用，同时保持马尔可夫框架［11-12］。在整个模型中，一旦随机上网者到达悬挂结点，他将立刻回到他所来自的那个页面，这个回弹式的特性尽在悬挂结点上对后退按钮进行建模，因此需要为指向每个悬挂结点的每条入链增加一个新的结点［13-14］，可以通过以下例子分析该回弹模型，图2对应的超链接矩阵H为：

图2　后退按钮模型中原来的6结点图

图3　后退按钮模型中原来的6结点图

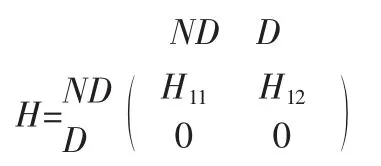
对每个指向悬挂结点的入链，生成一个回弹结点。将有nnz（H12）个这样的回弹结点，而不是悬挂结点集合中的个结点。如果每个悬挂结点都有不止一条入链，在存在很多悬挂结点的前提下，将极大增加矩阵的规模［15］。回弹超链接矩阵的分块形式：

4　结论

PageRank模型扩展到网络大小的规模时面临的问题的研究已经展现其有效性，研究方法和思路更加追求创新和效率，但是无论存储矩阵、PageRank的解的精度、收敛准则、悬挂节点等问题，目前的研究都还不尽完善。由于不同算法给出的列表彼此之间存在明显差别，因此未来的研究工作可以将多个相互独立的算法的结果加以融合。

［1］Barrett R，Berry M.Templates for the Solution of Linear Systems:Building Blocks for Iterative Methods［M］.SIAM，Philadephia，2nd edition，1994.

［2］Sriram Raghavan and Hector Garcia-Molina.Compressing the graph structure of the Web［M］.In Proceedings of the IEEE Conference on Data Compression，2001：211-215.

［3］Cleve B.Moler.Numerical Computing with MATLAB［M］.SIAM，2004.

［4］Sriram Raghavan and Hector Garcia-Molina.Representing web graphs［C］11In Proceedings of the 19th IEEE Conference on Data Engineering，Bangalore，India，2003.

［5］Krishna Bharat，Andrei Broder.The connectivity server:Fast access to linkage information on the Web［C］//In The Seventh WorldWideWebConference，Australia，1998：467-51.

［6］Paolo Boldi and Sebasiano Vigna.The WebGraph framework:Codes for the World Wide Web［R］.Technical Report 291-96，Universita di Milano，Dipartimento di Scienze dell' Informazione Engineering，2003.

［7］Paolo Boldi and Sebasiano Vigna.The WebGraph framework: Compression techniques［C］11 In The Thirteenth International World Wide Web Conference，New York，2004：590-610.

［8］William J.Stewart.Introduction to the Numerical Solution of Markov Chains［M］.Princeton University Press，2014.

［9］Grace E.Cho and Carl D.Meyer.Aggregation/disaggregation errors for nearly uncoupled Markov chains［R］.Technical report，NCSU Tech.2013.

［10］Chris Pan-Chi Lee and Gene H.Golub.A fast two-stage algorithm for computing PageRank and its extensions［R］.Technical Report SCCM-2009-15，Scientific Computation and Computational Mathematics，Stanford University，2009.

［11］Ronald Fagin and Anna R.Random walks with”back buttons”［C］//In 32nd ACM Symposium on Theory of Computing，2000.

［12］GraceE.ChoandCarlD.Meyer.Aggregation/ disaggregation errors for nearly uncoupled Markov chains［R］.Technical report，NCSU Tech.Report.2013.

［13］Carl D.Meyer.Matrix Analysis and Applied Linear Algebra［C］//SIAM，Philadelphia，2000.

［14］Michael W.Berry and Murray Browne.Understanding Search Engines:Mathematical Modeling and Text Retrieval［J］.SIAM，Philadelphia，2005（16）:78-93.

［15］PaoloBoldiandSebastianoVigna.TheWebGraph framework II.Codes for the World Wide Web［C］//Technical Report286-03，UniversitadiMilano，Dipartimento diScienze dell'Informazine Engineering，2013.

The study of PageRank mass storage problems

SHI Qian1，ZHANG Jia-jian2，ZHANG Wei2
（1.Business School of HOHAI University，Nanjing 210000，China；2.Jiangsu Posts&Telecommunication Planning and Designing Institute Co.Ltd，Nanjing 210000，China）

PageRank model is expanded to the size of the network size when faced with how to store solution accuracy，convergence criteria of the matrix，hanging nodes.Search engine will require a huge amount of storage facilities to archive the web and its location，inverted index and image index，content，grading，PageRank score and hyperlink graph information.At the same time，PageRank large-scale implementation must make decisions on design to determine how to deal with hanging nodes problem.In this paper，we study mathematics content of link analysis algorithm and the mathematical elements PageRank part of storage，hanging nodes and modeling problem of the back button.

PageRank；storage problem；hanging nodes；modeling problem of the back button

TN0

A

1674－6236（2016）17-0004-03

2016-02-26稿件编号：201602157

江苏省社科联研究基金（201035）；中央高校基本科研业务费项目（2010B10714）

史倩（1987—），女，江苏南京人，硕士。研究方向：企业管理、技术经济。