基于SIMULINK的车辆防抱死制动系统控制研究
李振兴 周晶晶

摘要: 利用Simulink软件建立车辆防抱死制动系统的仿真模型;基于PID控制原理设计以车轮滑移率为控制对象的防抱死制动系统控制器,对防抱死制动控制系统进行仿真。将普通制动系统与防抱死制动系统仿真结果进行对比,结果表明PID控制的防抱死制动系统能有效提高车辆的方向操纵性和制动效能。
Abstract: Firstly, the simulation model of Anti-lock braking system is established by the software of simulink; Secondly, this paper designs a kind of Anti-lock Braking System(ABS) controll system and targeted at the wheel slip ratio based on the PID control strategy, which simulated the system of ABS and analysed the result. The simulation results of the ordinary brake system is contrasted with the Anti-lock braking system, and the results show that PID control ofAnti-lock braking system can effectively improve the direction of the vehicle maneuverability and braking performance.
关键词: 防抱死制动系统;PID;仿真
Key words: anti-lock brake system;PID;simulation
中图分类号:U463.33 文献标识码:A 文章编号:1006-4311(2016)07-0102-03
0 引言
汽车防抱死制动系统是提高车辆行驶安全的重要装置[1]。它能防止车辆在制动时车轮抱死滑移,保障车辆的行驶稳定性和转向操纵性,同时能有效地缩短制动距离,减少交通事故的发生。
防抱死制动系统中最重要的部件是防抱死制动控制器,它决定了防抱死制动系统系统的性能,而控制器的核心是控制算法的选择。目前大部分车辆上采用的是基于经验的逻辑门限控制方法,它的方法简单实用,但调试比较困难,采用经验的方法,不同的车辆需要不同的匹配技术,需要比较多的道路试验加以验证,算法实施复杂而且鲁棒性不强。PID控制算法原理简单,使用方便;适应性强;鲁棒性强。因此,应用PID控制理论,在SIMULINK中仿真研究防抱死制动系统的控制策略及其控制效果。
1 系统模型建立
1.1 单轮车辆模型
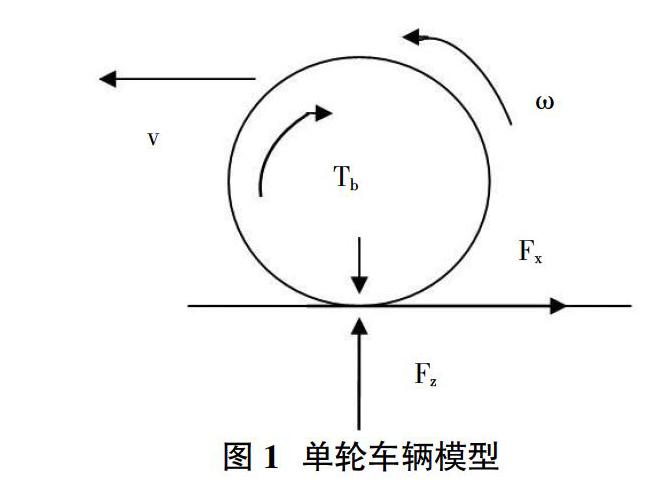
为简化研究问题,采用单轮车辆系统模型如图1所示,忽略空气阻力和车轮滚动阻力;车辆质量均匀分布在每个车轮上,轮胎的机械特性相同;车辆在水平公路上行驶[2]。
根据图1,得到车辆动力学方程:
式(1)~(3)中:m为1/4车辆质量;v为车辆纵向速度;Fx为车轮纵向附着力;I为车轮转动惯量;?棕为车轮转动角速度;R为车轮半径;Tb为制动力矩;?滋为车轮与地面间的附着系数;Fz为地面对车轮支撑力。
1.2 车轮轮胎模型
轮胎模型是指车辆在制动过程中,附着系数和各相关参数之间的函数关系[3]。轮胎的附着系数受多种因素影响,除了滑移率,还有轮胎的花纹、材料及路面的状况等。在实际情况下,人们在建立轮胎模型时很难将所有的影响因素都考虑进去,只考虑了对附着系数影响大的因素。目前,人们常用的轮胎模型有魔术公式轮胎(经验公式模型)和双线性公式模型(半经验公式模型)两种[4]。
采用双线性公式模型,其拟合精度较高,计算方便,比较适合用于模拟仿真研究。
表达式如下:
滑移率的表达式如下:
滑移率常用来衡量制动时车轮的滑移程度,车轮在纯滚动时滑移率为0;车轮抱死在纯滑动时滑移率为100%;车轮边滚动边滑动时滑移率在0~100%之间。实验证明,滑移率在15%~20%时附着系数最大,制动效果最佳。
1.3 车辆制动系統模型
制动系统模型包括传动机构模型和制动器模型两部分。采用液压传动机构,为简化模型,忽略压力传送的延迟因素和电磁阀环节,液压传动系统简化为一阶惯性环节和一个积分环节[6]。由于电磁阀的响应时间通常小于等于10 ms,所以液压传动系统的一阶惯性环节的传递函数为:
制动器模型指的是制动器力矩和制动液压之间的关系的模型,建模前假定制动器为理想的元件,理解为其非线性特性比较弱且不计其滞后所产生的影响。制动器表达式如下:
2 PID控制器设计
PID控制器是一种线性控制器,是根据设定值与实际输出值的偏差作为控制器的输入信号。PID的控制算法如下式:
式(8)中,Kp为比例放大系数,比例系数增大,控制系统的余差减小,但振荡加剧;Ki为积分系数,其数值过大,降低控制系统的稳定性;Kd为微分系数,其数值增大,减小系统的超调量,减小调节时间,但过强会导致系统稳定性降低。
设计的PID控制器是以车轮滑移率为控制目标,通过传感器采集汽车行驶过程中的车速和轮速信息,计算出车轮的实际滑移率。车轮的实际滑移率与期望滑移率之间的差值即为PID控制器的输入,输出为制动器压力。控制策略如图2所示。
比例系数、积分系数和微分系数的参数选择决定了PID控制器的控制效果。按照先比例,再积分,最后微分的顺序进行参数的设定。经多次调试后的PID控制器的参数为Kp=230,Ki=200,Kd=3。期望滑移率为0.2。根据上述控制策略和参数,设计PID控制器仿真模块如图3所示。
3 控制系统仿真
根据上述车辆模型数学表达式及设计的PID控制器,在SIMULINK软件中建立防抱死制动控制系统仿真模型,模型如图4所示。
选取某轿车为研究对象,主要仿真参数如下:1/4车辆质量=390kg;车轮半径R=0.268m;车轮转动惯量I=1.4852kg·m2;初始车速v=20m/s;路面参数选择高附着系数。求解器选取变步长模式ode45s,仿真时间设定为3秒。
4 仿真结果与分析
制动系统的性能评定指标有:制动距离、制动时间、车轮滑移率、制动减速以及制动时地面的附着系数等。
在仿真结果中选取车轮滑移率与时间关系曲线;制动减速度与时间关系曲线;地面附着系数与时间关系曲线;车速&轮速与时间关系曲线以及制动距离。对比普通制动系统与有PID控制的防抱死制动系统的仿真结果,如图5~9所示。
从图5~9可以看出,在没有防抱死制动控制的普通制动情况下,车速从20m/s到车辆完全停止经过了2.97秒,而轮速经过0.22秒后就下降到0,同时滑移率为1,车轮出现抱死状况。制动距离为30.29m,制动减速度在6.85左右,同时地面的附着系数为0.7。加入PID防抱死制动控制环节后,车辆由初始速度20m/s到车辆停止用时为2.65秒,整个制动过程中,车轮转速没有迅速下降到0,而是随着车速一起变为0,车轮没有出现抱死状况,并且车轮滑移率始终在期望值0.2附近。制度距离为27.45m,制动减速度在7.85左右,同时地面的附着系数为0.8。由此可见PID控制下的防抱死制动系统具有良好的控制效果,与常规制动相比,制动时间缩短了10.7%,制动距离减少了9.4%,同时滑移率在期望值附近,并且在整个过程中无较大波动情况,稳定性较好。
5 结语
在制动系统车辆模型的基础上,运用PID控制理论,基于SIMULNK平台研究以滑移率为控制目标的车辆防抱死制动系统。通过仿真对比分析,PID控制的防抱死制动系统能有效的提高车辆制动时的方向操纵性和制动效能。
参考文献:
[1]余志生.汽车理论[M].北京:机械工业出版社,2000.
[2]喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2004.
[3]程军.汽车防抱死制动系统的理论与实践[M].北京:北京理工大学出版社,1999.
[4]叶磊,尹作发.基于Matlab/Simulink的车辆制动过程分析[J].公路与汽运,2006(6):5-7.
[5]M.Gavas, M.Izciler. Deep drawing with anti-braking system(ABS)[J]. Mechanism and Machine Theory, 2006,Vol41(12):1467-1476.
[6]程軍.汽车防抱死制动系统的控制方法分析[J].汽车技术,1992(10):1-8.

