基于Matlab的PE—600*900复摆颚式破碎机破碎腔优化设计
王晓敏 张高青 孟彩茹
摘 要:颚式破碎机广泛应用于矿山、建筑、交通等多种行业中,这是由于颚式破碎机机构结构简单、机型比较齐全且已经大型化、通用化。虽然颚式破碎机的机构已经日趋完善,但是随着社会的飞速发展对破碎的要求及产品的质量要求也在不断提高,破碎机的现有机型已经不能满足发展要求。而破碎机破碎腔的结构、尺寸对破碎能力和质量有着关键性的影响。文章设计的内容是PE-600*900复摆颚式破碎机的破碎腔优化设计,着眼于动颚板的轨迹曲线,从而计算出破碎腔的变化。首先计算出有效破碎空间的体积,将其作为目标函数在Matlab进行优化设计,得到其分布合理、生产能力高的相关参数等。
关键词:复摆颚式破碎机;破碎腔;Matlab;优化设计
引言
复摆颚式破碎机是一种非常简单的结构,可靠,易于制造,维修方便,故此,复摆颚式破碎机目前被广泛使用在冶金,建材,化工,煤炭等行业,并致力于破碎一直在使用的碎石及其他工业原料[1]。然而,其缺点是非连续性破碎、效率较低,破碎比较小,给矿不均匀引起颚板磨损不均匀等[2]。针对其缺点,文章将优化动颚板运动轨迹改进破碎腔型,以增大破碎比,提高破碎效率,减少磨损,降低能耗。
1 破碎机机构分析
1.1 复摆颚式破碎机结构
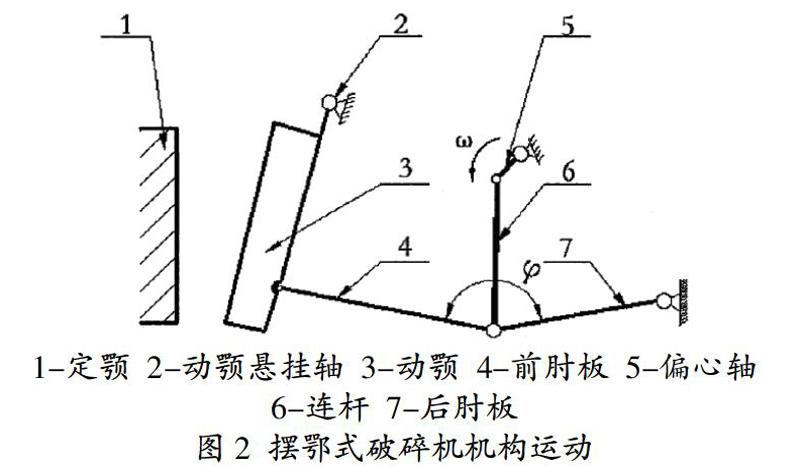
颚式破碎机的结构主要由机架、偏心轴、大皮带轮、飞轮、动颚板、定颚板、肘板、肘板后座、调隙螺杆、复位弹簧等组成[3]如图1所示,其中肘板还起到保险作用。
1.2 破碎腔有效破碎空间
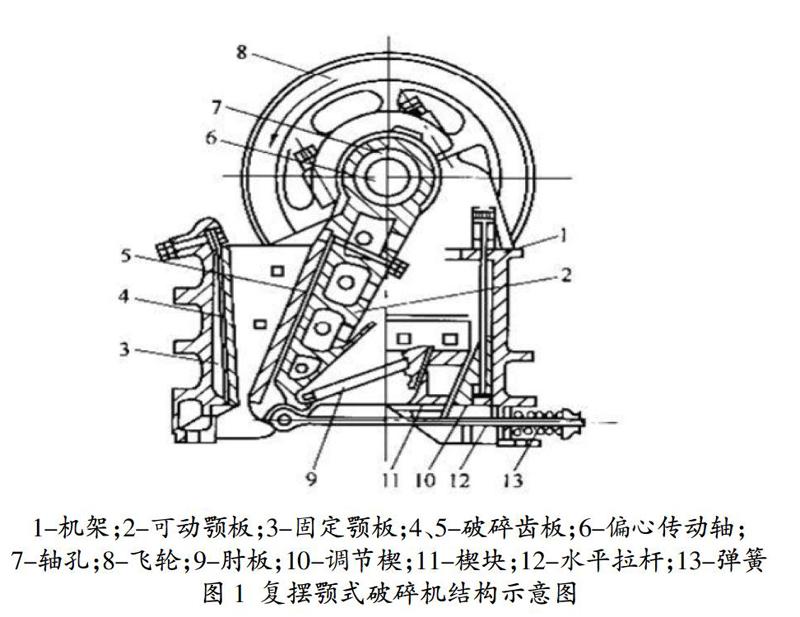
如图2所示,电动机的动力通过皮带传动偏心轴5传递,偏心轴的转动使连杆6上下往复运动。当与偏心轴连杆向上转动,角度会逐渐变大,从而拉动动颚3,并使它靠近定颚1。此时在破碎腔中,定颚之间的空间会逐渐减小,破碎材料进行挤压破碎。当与偏心轴连杆向下转动,角度会逐渐变小,从而拉动动颚,并使它远离定颚。此时在破碎腔中,定颚之间的空间会逐渐增加,破碎材料易于从粉碎腔的排出口排出。由此可见,动颚作周期性往复运动,动颚与定颚之间的间距发生变化,破碎腔也发生变化[4]。
从上面的分析可知,在动颚运动过程中不是整个破碎腔同时破碎和同时排料,而是部分破碎腔产生破碎,另一部分不破碎。有效破碎空间即是破碎腔中进行实际破碎的空间。下面通过分析动颚的运动状态来研究有效破碎空间的变化规律。
2 有效破碎空间理论计算
2.1 动颚速度瞬心方程式建立
由平面图形速度瞬心定理知,动颚绝对速度瞬心位置随曲轴(即曲柄)旋转角度的变化关系没曲柄的回转中心为坐标原点,建立的直角坐标系及机构简图如图3所示。
动颚的速度瞬心从右边间断点向左边间断点连续变化,经O1点到B点,再向左直到左边间断点;紧接着又从右边间断点开始向左连续变化直到左边间断点,如此往复循环[5]。
可以看出,动颚的平面运动使其上下端点并非时刻同步运动只有当曲柄转至与摇杆平行位置时,动颚才有斜向左或斜向右平移的趋势。除此之外,连杆都绕速度瞬心作回转运动,即上端点远离定颚,下端点靠近定颚;上端点靠近定颚,而下端点原理定颚;或上端点和下端点同时靠近或原理定颚,但速度方向不同。
已知曲柄OA=L1,连杆AB=L2,摇杆BO1=L3,机架OO1=L4,点O1的坐标为x=-r,y=-h,机架与y轴的夹角为α,假定曲柄从x轴正向出发,逆时针转过角度Ф时,则曲柄质心方程为:
y=xtan?准 (1)
由图3可知, ,分别过点A、B作y轴的平
行线O1F,过A作AP平行于OO1,并连接AO1,由此得出:
(2)
因此摇杆BO1的方程式为:
由三心定理可知,OA与O1B两直线的焦点即为动颚AB的速度瞬心,因此连立(2)和(3)式可得动颚速度瞬心随曲柄旋转角变化的方程式:
(4)
2.2动颚齿板上下端点运动坐标方程式
以PE-600*900行复摆颚式破碎机为例进行分析。该破碎机动颚的运动状态如图2所示,摇杆水平位置时,复摆颚式破碎机的破碎运动达到破碎运动的极限位置,破碎运动结束;当曲柄OA继续转动,带动摇杆BO1继续向下摆动,同时连杆AB的速度瞬心从无穷远沿着BO1的延长线逐渐向O1靠近,此运动为排料运动;直到曲柄OA与连杆重合的时刻,排料运动结束。
根据图2和图3 可求动颚上下端点的运动方程式:
(5)
由此可得连杆AB的方程式为:
2.3破碎机有效破碎空间的大小
有效破碎空间是衡量破碎腔大小的标志量,也是计算破碎机破碎力的重要依据。因此需要运用解析几何的知识计算出复摆颚式破碎机有效破碎空间的具体计算公式。
假设破碎腔为一个以梯形为底,以动颚宽为高的一个类梯形的体积来求解。
设k是AB的中点由(5)式可以得出:
(7)
梯形的面积为: (8)
所以这个破碎腔的体积可以是:
V=F(k)*h*B (9)
由破碎机参数可知:h=1440mm,B=800mm,L1=12mm,L2=1337mm。
3 破碎空间的优化设计
3.1 优化模型
当摇杆水平位置时,动颚恰好处于破碎过程恰好结束时,此时的破碎腔空间出现最小值,此时的 ,当摇杆和连杆共线时,此时的破碎空间出现最大值,此时 。
当破碎腔体积出现瞬时最小时,
当破碎腔体积出现瞬时最大时,
设目标函数为:
自变量为:ɑ。
3.2 Matlab优化仿真
利用Matlab优化工具箱进行编程仿真,结果如图4所示。
仿真结果显示,ɑ=23.2174°时,有效破碎空间取最大值,最大有效空间为:
ΔVmax=1.4867*107mm3
4 结束语
文章在现有PE-600*900颚式破碎机的基础上进行优化设计,选取变量α并经过计算得出目标函数,最终在MATLAB中进行计算,绘制图谱,得出最优解。研究表明,倾角α的变化对有效破碎空间的影响很大,并求出了α的最优解,达到本次設计的目的与要求。
参考文献
[1]周素琴.基于运动学和有限元分析的颚式破碎机结构改进的研究[D].昆明理工大学,2014.
[2]赵月.复摆颚式破碎机强度的有限元分析[D].浙江大学,2013.
[3]刘长福.颚式破碎机的运动学及动颚的机架的仿真与优化[J].太原理工大学,2002.
[4]李磊.颚式破碎机能耗和齿板结构参数研究[D].中南大学,2009.
[5]陈建中,沈丽娟,赵跃民.选矿机械[M].中国矿业大学出版社,2012.

