从一个电路的多种解法探讨电路的分析方法

陈寨群

摘要：电路是物理教学中的重要内容，其中涉及到大量的物理专业知识，是对自然界中电力学知识点的探究与学习。在同一个电路之中，电路分析思维、角度的不同，会产生多种不同的解法。通过对线性电阻电力运行情况的基本分析，了解到多种解法的分析都存在着联系，每个思维方式与动态、稳定的电路系统都是相互适用的。为此，本文就从一个电路的多种解法谈电路的分析方法进行了分析与探究。

关键词：电路；多种解法；计算

在线性电阻电路系统之中，元件的相关参数、电路系统结构等是重要前提，在此状态下进行激励，定会产生一定的影响，是当前电路分析的重要突破口。通常意义上，电路分析的方法主要包括支路电流法、等效变换法、叠加原理、网孔电流法、节点电压法、戴维南定理、诺顿定理七种，在本文中挑选了其中五种进行分析[1]。在电力学领域都得到了广泛的应用。在学习这些电路分析法时，由于思维抽象，电路相关参数计算复杂，成为学生学习的重要阻力。因此，以下就这些方法进行具体的分析。

如图1所示，此为线性电路，其中各部分元件所对应的参数已知，对1Ω电阻上所存在的电流参数进行求解。在图1中，设置了足够的电流源与电压源，虽然从表面上看难度不大，但是这是无法利用欧姆定律来进行求解的，该电路相对复杂，可选择很多方式进行求解。

1、 支路电流法

支路电流法是将支路电流作为未知量而展开的电路分析，对电路系统中电压与电流的关系予以了解，还要对电路系统中回路的KVL与支点部分的KCL约束关系进行控制。此外，还应设立方程组，可对各个支路部分的电流进行合理的计算。如图1所示，若电压为12V的电压源与电阻值为2Ω的电阻进行串联，电流的参考方向为I1，在那两个节点处列出KCL方程：I1+3=I，与此同时，在左边应列KVL方程：2I1+1I-12=0[2]。将列出的这两个方程进行联立，最终求解出电流值为I=6A。在使用支路电流法时，必须及时掌握网孔、节点与支路的个数，保证支路的数量与支路电流参数个数的一致性，若节点为n个，KCL方程的数量为n-1，若网孔的数量为m，KVL方程的数量就为m个。通过此方式所罗列出的方程数量与未知量的数量一致，最终将结果求解出来即可。若在求解的过程中，遇到该电路中存在一定的电流源，也就确定了某支路的电流，在列KVL方程时必须要将电流源的回路进行避开处理，运用此方式保证未知量的数量不会增加，计算更为简便。

2、 等效交换法

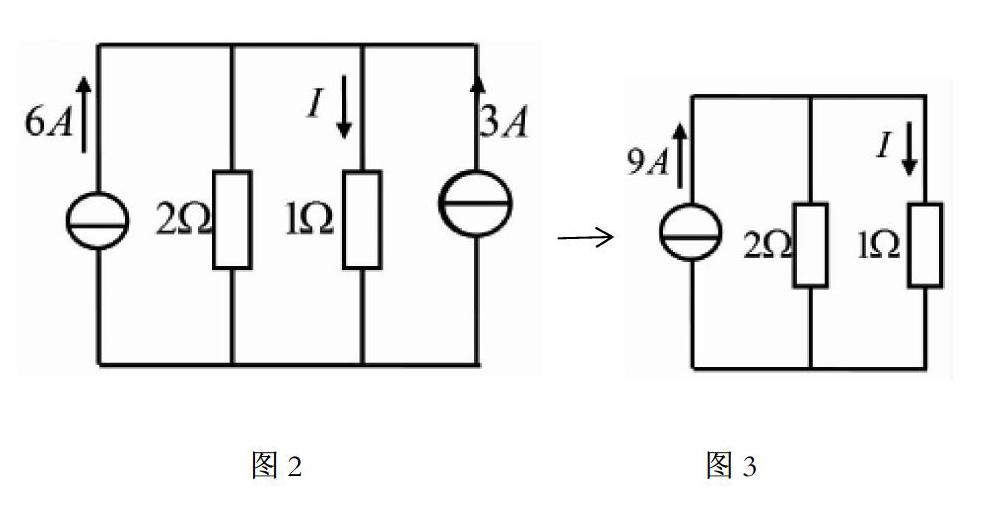
对于所有实际存在的电源而言，其可使用内阻理想电压源串联与并联的模型进行表示。由此可见，若同属一个电路，实际电流与电压源能实现等效交换，一个电流源和电阻的并联与一个电压源和一个电阻的串联是相互等效存在的[3]。将图1中电压为12V的电压源与电阻值为2Ω的电阻串联，与方向向上的6A电流源和电阻值为2Ω的电阻的并联进行等效，等效连接如图2所示。其次，应将两个并联在一起的电流源进行合并处理，合并后电流方向为向上，电流值为9A，如图3所示。对图3进行分析，以计算出电流值 I=9×2/（2+1）=6A。为了保证电流值的有效计算，应及时画好等效图，在电压源和电流源变换的前后处，应注意电路模型在参考方向上的设置，应始终保持相反的状态。

3、叠加原理

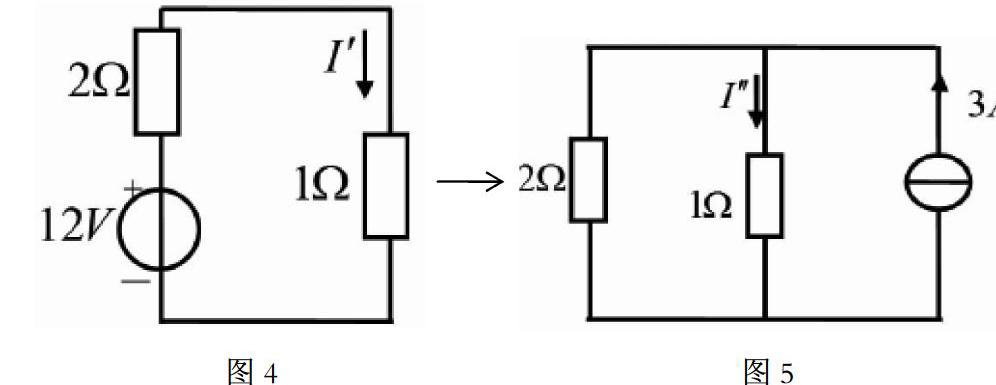
叠加原理是指在线性电路中，在同一电路中存在多个电源，这些电源会作用在电压或电流之上，运用此方式也等同于电源分别单独作用在该支路上所产生的电压或电流的代数和[4]。若12V的电压源单独运行时，进而产生等效图4，I′=12/（2+1）=4A；若3A电流源进行单独运行时，会产生等效图5，I"=3×2/（2+1）=2A。最终，将这两个进行叠加，I=I'+I"=4A+2A=6A。不过，此方法仅仅能用来计算现行电路中所产生的电流与电压，无法对功率进行计算。叠加操作时，要对电压与电流的参考方向进行确定，并最終求出代数和。若电流或电压的参考方向与原电路的参考方向一致，电压或电流的参数应取正值，反之，则取负值，在对参数进行计算时，必须保持严格、谨慎的态度，以达到理想的计算效果。

4、 网孔电流法

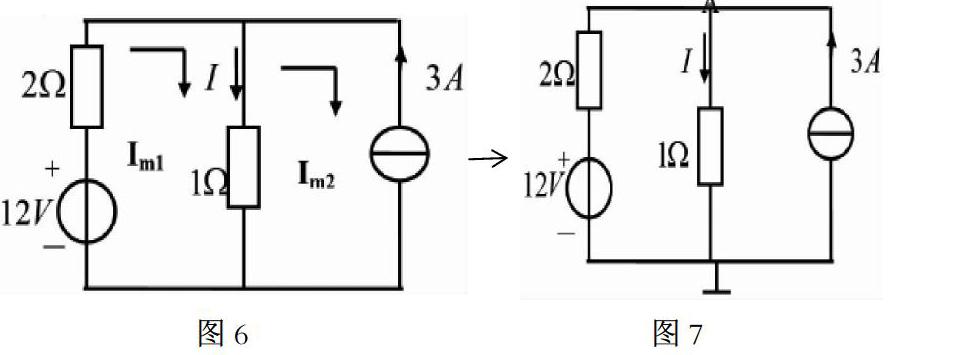
网孔电流法是将拟定的网孔电流作为重要的未知量，采用KVL来列写电压方程，进而实现对电路分析的一种重要方法。在图6中，存在两个网孔，拟定这两个网孔的电流分别为Im1、Im2，顺时针方向进行循环，左边的网孔中，若将电流Im1设定为正向，在2Ω的电阻上电流的数量为1个，即Im1，1Ω电阻上电流数量为2个，一个为正电流Im1，一个为负电流Im2，列出KVL方程2×Im1+1×Im1-1×Im2=12。在右边的网孔中，若将电流Im2设定为正向，则Im2=-3A。对这两个方程组进行联立，最终得出Im1=3A，进而得出I=Im1-Im2=3-（-3）=6A。

图6 图7

5、节点电压法

节点电压法的实施，要先选择好的参考点，除了该参考点外要将其它位置的节点进行标注，将节点的电压设定为未知量，以欧姆定律为重要依据来对各支路的电流进行求解。图1中，若设置参考点，必须保证其接地，如图7中所示，应及时列出方程：VA/1+VA/2=3+12/2，由此可得VA=6A。节点电压法适用于节点相对较少的电路，在对方程进行设定时应及时做好正负号的转换。

结束语：

综上所述，通过对电路分析方法的了解，意识到在同一个电路系统中，其分析方法呈现多元化的趋势，当然必须是建立在分析方法与电路相适应的基础之上，这样会大大减少计算量，进而提高解题质量。由此可见，当对一个电路图进行分析时，不可立即进行计算，而是要找寻电路中的线索，从待求参数着手，以电路图提供的已知条件为重要前提，进而开展推理工作，最后从中筛选出最为简单的方法进行解题。

参考文献：

[1]刘显奎，方志聪.从一个电路的多种解法谈电路的分析方法[J].西昌学院学报（自然科学版），2011，4（4）：37-72.