汽车控制臂焊接应力变形的分析和控制

李卓明 熊璐

摘 要：本文采用有限元软件ANSYS对某款汽车控制臂的焊接应力变形进行分析研究，建立焊接应变和焊接尺寸之间的关系，并通过优化焊接顺序和焊接方向寻找控制应力变形量的最优解。仿真及试验结果表明，长焊缝的焊接顺序布置在短焊缝之间对焊接后变形量的影响相对最小，且当两侧焊接方向异向时效果最佳。

关键词：控制臂；有限元分析；焊接應力变形

汽车控制臂是悬架系统的重要焊接结构部件之一，对汽车的行驶平顺性和操纵稳定性有很大的影响。焊接作为其主要的加工工艺，在保证产品尺寸精度、强度要求的过程中扮演着举足轻重的角色。而焊接变形又是影响结构设计完整性、制造工艺合理性和结构使用可靠性的关键因素。因此，对汽车控制臂在焊接过程中所产生应力变形的预测及控制的研究显得尤为重要。

本文利用有限元软件ANSYS模拟分析某款汽车控制臂的焊接应力变形情况，然后通过控制臂在不同方向上的应变值及尺寸、形位公差的定义建立焊接应变和焊接尺寸之间的关系，最后再利用有限元法模拟焊接顺序和焊接方向对焊接尺寸的影响，并通过方案对比和试验验证寻求最优解。

1 控制臂焊接应变分析

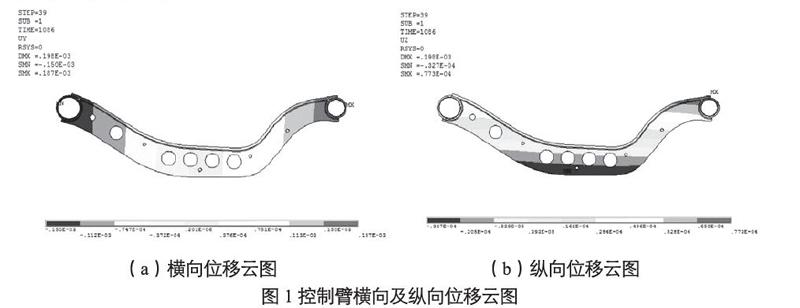
控制臂在产生焊接残余应力的同时还将发生应力变形，通过ANSYS中Contour Plot功能可以获得横向（Y向）及纵向（Z向）的位移云图，见图1。

（a）横向位移云图 （b）纵向位移云图

图1 控制臂横向及纵向位移云图

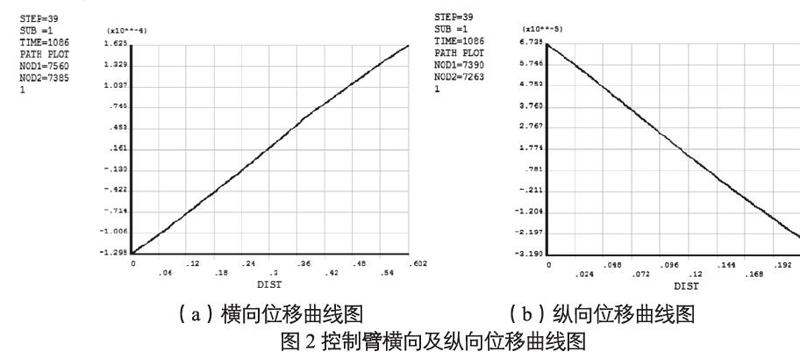
为进一步了解控制臂横向和纵向各个截面上的位移分布情况，在控制臂连接片横向和纵向上分别设置一条路径，然后计算各条路径上的位移值，见图2。

（a）横向位移曲线图 （b）纵向位移曲线图

图2 控制臂横向及纵向位移曲线图

从各条路径的位移曲线上能看出，控制臂在横向和纵向上的位移和路径之间有着一定的规律，即控制臂左端至右端的横向位移从最大负位移逐渐转换到最大正位移，且右端比左端有更大的位移；控制臂上端至下端的纵向位移从最大正位移逐渐转换到最大负位移，且上端比下端有更大的位移。

2 焊接应变及焊接尺寸关系建立

要把焊接应变与焊接尺寸准确合理地统一起来，必须先了解总成焊件下线后的检测状态，并根据理想状态的焊件检测时的主定位建立基准坐标系再由各个方向上的焊接应变值通过计算后转变为焊接尺寸值。由于该焊件的主定位为控制臂大套筒处的定位小孔，因此先将焊接理想状态下控制臂的定位小孔的中心设定为基准坐标系的原点，再分别根据控制臂焊接的主要尺寸要求结合其Y、Z方向上的残余应变值进行求解转换，如下：

2.1 大小套筒中心距离：562.5±0.5mm

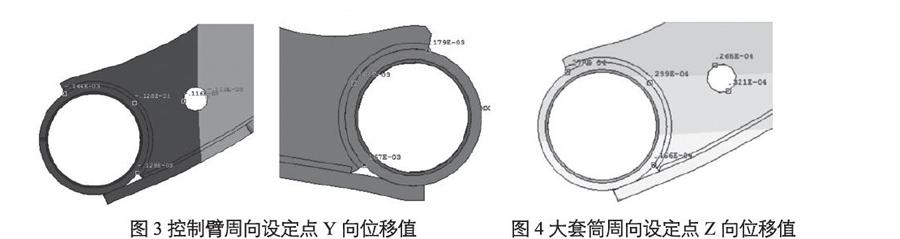
分别在大套筒的周向上设定3个点；在定位孔的周向上设定2个点；在小套筒的周向上设定3个点，如图3所示。大套筒周向3个节点的Y向位移平均值为-0.133mm；定位孔周向2个节点的Y向位移平均值为-0.113mm；小套筒周向3个节点的Y向位移平均值为0.171mm。按照基准坐标系进行转换：大套筒Y向平均位移为-0.02mm；小套筒Y向平均位移为0.284mm。因此，大小套筒中心位移为0.304mm。

2.2 大套筒位置度：

分别在大套筒的周向上设定3个点；在定位孔的周向上设定2个点，如图4所示。大套筒周向3个节点的Z向位移平均值为0.035mm；定位孔周向2个节点的Z向位移平均值为0.029mm。按照基准坐标系进行转换：大套筒Z向平均位移为0.006mm，由于大套筒Y向平均位移为-0.02mm，因此，大套筒位置度为0.042。

图3 控制臂周向设定点Y向位移值 图4 大套筒周向设定点Z向位移值

2.3 大套筒端面与连接片表面距离：7.5±0.5mm

分别在大套筒的端面上设定2个点；在定位孔的端面上设定2个点，如图5所示。大套筒端面2个节点的X向位移平均值为0.002mm ；定位孔端面2个节点的X向位移平均值为-0.001mm。按照基准坐标系进行转换：大套筒端面与连接片表面距离为0.003mm。

2.4 小套筒端面与连接片表面距离：7.5±0.5mm

在小套筒的端面上设定2个点，如图6所示。小套筒端面2个节点的X向位移平均值为0.003mm。按照基准坐标系进行转换：小套筒端面与连接片表面距离为0.004mm。

图5 大套筒端面设定点X向位移值 图6 小套筒端面设定点X向位移值

从实际检测上来看，大套筒Y向实际检测转换值为-0.158mm；Z向实际检测转换值为-0.075mm；小套筒Y向实际检测转换值为0.392mm；大套筒端面与连接片表面X向距离的实际检测转换值为-0.18mm；小套筒端面与连接片表面X向距离的实际检测转换值为-0.11mm。由于上述各项尺寸的实际检测转换值和计算机模拟转换值之间的差异均小于焊接尺寸公差的20%，还要考虑焊接热辐射、熔池流体流动等综合因素的影响，因此，本文认为该差异在合理的范围内。

3 焊接顺序和方向优化对焊接尺寸的影响

在本次研究中，按照变位机的工作原理和焊接就近原则主要选择了6个不同焊接顺序和方向的方案进行模拟仿真计算。控制臂具体焊缝位置如图7所示。

图7 控制臂焊缝位置图

一般而言，由于焊件的长焊缝所引起的焊接残余应力及变形最为显著，因此根据控制臂的长焊缝3L、3R处于的不同焊接顺序位置，将以上6个不同的方案分为3组进行后续的对比研究。表1为6套方案经过焊接模拟仿真计算后的焊接尺寸数据对比表。

表1 控制臂焊接方案结果对比表

从中可以看出，此款控制臂焊接顺序和方向的变化主要影响的焊接尺寸是大小套筒中心距离，对大小套筒端面与连接片表面距离以及大套筒位置度的影响可以忽略不计。此外，第一组方案得到的大小套筒中心距离的公差值最小，即长焊缝的焊接顺序布置在短焊缝之间对焊接后变形量的影响相对最小，且当两侧焊接方向异向时效果最佳。

4 结语

本文建立了汽车控制臂焊接应变及焊接尺寸之间的转换关系，并在这基础上进一步探讨了焊接顺序和方向对焊接尺寸的影响，不仅为提升焊接尺寸符合率提供了可靠的理论依据和指导，同时也促进了有限元分析技术在汽车零部件焊接应力变形的预测和优化方面的工程应用。

参考文献：

[1] 张海波，张瑞军，常影.基于ANSYS的汽车悬架控制臂有限元分析[J].组合机床与自动化加工技术.2014（03）：150-151.

[2] 周方明，王华杰，赵永昌，等.基于有限元法的底盘结构件焊接变形预测及优化[J].江苏科技大学学报： 自然科学版.2012（04）：337-340.

[3] 杨建奎，江克斌，翟可为.基于ANSYS的辐射和相变对焊接温度场的影响研究[J].机械工程与自动化.2012（01）：60-62.

[4] 祝小元，方宗德，申闪闪，等.汽车悬架控制臂的多目标拓扑优化[J].汽车工程.2011（02）：138-141.

[5] 上官文斌，田子龙，王小莉，等.汽车悬架系统中的橡胶-金属元件[J].现代零部件.2009（06）：86-88.

[6] 刘新田，姚颂氢，黄虎，等.后双横臂独立悬架的下控制臂有限元分析[J].上海工程技术大学学报.2009（03）：191-193.

[7] 蒋振辉，范灏，许黎明，等.汽车悬架控制臂前衬套自动化压装原理与实现方法[J].制造技术与机床.2015（10）：34-36.

[8] 王培岗.汽车悬架系统控制器的优化设计[J].电子世界.2014，（04）：97.