内含报酬率的求解及多解问题分析

冀聪慧

摘要：内含报酬率（IRR）作为投资项目评价的重要指标，应用比较广泛。传统求解IRR的方法计算复杂、精确度不高；而财务中常用的软件Excel操作简单、结果准确，但对于多解问题没有比较普及的求解方法。文章分别介绍了常规项目和非常规项目的IRR在Excel中的求解方法，并在非常规项目IRR的多解问题上，从其经济内涵出发提出了排除方法。

关键词：内含报酬率 Excel 多解问题

中图分类号：F234 文献标识码：A 文章编号：1002-5812（2016）15-0087-02

内含报酬率（IRR）是项目投资决策中一个重要的动态评价指标，将它与资金成本率比较，可以反映出该项目的可行性，相比于一些绝对量指标更能直观地评价投资项目；另外，内含报酬率在不需要基准折现率的情况下就能求解出来，其值的大小不受外部参数的影响而完全取决于项目本身的现金流量，因此在财务领域被广泛应用。众所周知，内含报酬率是指投资项目的净现值等于零时的贴现率，计算公式为：

其中：IRR为内含报酬率，CFt为第t年的现金流量，n为项目的存续期。对于单一的投资方案，若求得的内含报酬率高于企业的资金成本率，则可以接受该投资方案，否则，应该拒绝该投资方案；在进行多个互斥的投资方案决策时，应该选择内含报酬率最大的投资方案。

一、传统求解方法的缺陷

对于内含报酬率的求解，传统方法为插值法，若要使计算结果贴近IRR的真值，必须使所取的插值区间尽可能地小，所以确定插值区间是插值法的关键。确定插值区间的一般做法是：当投资项目每年的现金流量相等时，采用“查表法”，计算出投资项目的年金现值系数，查年金现值系数表，找出对应的折现率区间即为插值区间；当每年的现金流量不相等时，采用“逐次测试法”，通过试误，找到使净现值出现一正一负的两个值。

然而，传统方法在应用过程中存在明显的缺陷。其一，在确定插值区间时，“查表法”要求投资项目每年的现金流量相等，条件苛刻，这样的投资项目在现实生活中几乎不存在；若采用“逐次测试法”，计算复杂、手工计算量大，尤其当各期净现金流的数量较多时，若第一次测试用的折现率远离目标利率，还会增加测试工作量。其二，“插值法”本身准确度不高，它是一种“以直代曲，按比例计算”的方法，无法得出准确的值，由于净现值曲线是与水平线渐近的曲线，确定直线的两点分别在横轴的两侧，所以用“插值法”计算出的内含报酬率的近似值大于内含报酬率的真实值，这种误差如果不加以有效控制甚至可能影响决策的正确性，因此要提高内部收益率评价的效果和准确性，就要寻求新的计算方法。

二、Excel求解方法

鉴于传统求解方法的不足，下面对在Excel中求解IRR进行举例说明：

（一）常规项目的IRR求解。

例1：假设某公司将200万元用于某项六年期的投资，第1—6年的净现金流量分别为45万元、50万元、60万元、70万元、65万元、55万元。试计算此方案的内含报酬率。

1.IRR函数法。（1）选定一张Excel工作表，在A1—A7单元格依次输入初始投资额及各年的现金流量，即： -200，45，50，60，70，65，50（注：初始投资额用负数表示）。（2）在单元格B1输入“=IRR（A1∶A7）”，并“回车”，即可得到内含报酬率的值：16.81%。

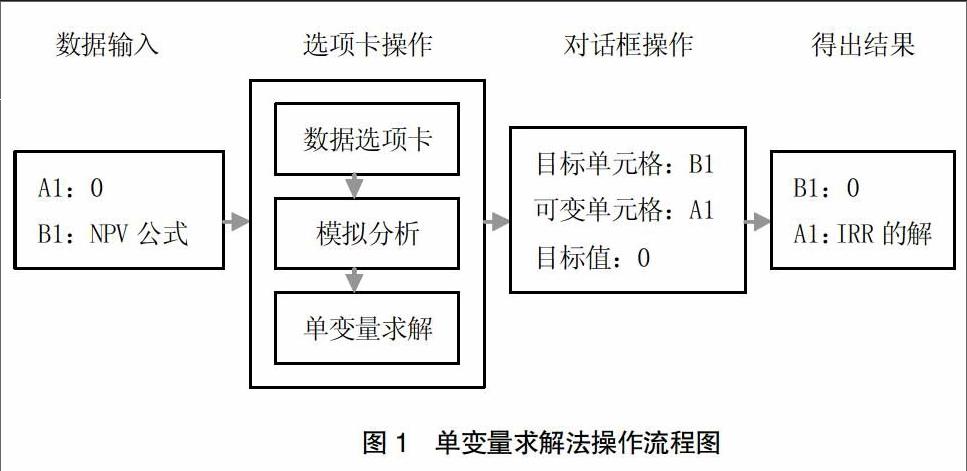
2.单变量求解法。（1）选定一张Excel工作表，在单元格A1输入0，在单元格B1输入净现值NPV公式“=NPV（A1，45，50，60，70，65，50）-200”。（2）单击“数据选项卡”→“模拟分析”→“单变量求解”，弹出“单变量求解”对话框。其中，“目标单元格”选择“B1”，“可变单元格”选择“A1”，目标值输入0，点击“确定”，显示单变量求解状态，当B1单元格值为0时，A1单元格的值16.81%就是解。操作过程如图1所示。

例1是一个常规项目，常规项目是指投资发生在初期、以后各年发生连续的净现金流入的项目。对于常规项目来说，IRR最多有一个解；而非常规项目的现金流符号变化两次或两次以上，根据笛卡尔关于高次方程的符号规则：系数为实数的高次多项式，其正实根的数目不会超过其系数序列符号的变更次数，当净现金流量序列有两次或者多次符号变化时，可能出现多个正值的内部收益率，这时按照前面的求解步骤不能求出所有的IRR值，下面对非常规项目的IRR求解原理进行分析并说明其步骤。

（二）非常规项目的IRR求解。

例2：某公司初始投资额为900万元，第1—5年的净现金流量分别为1 200万元、987万元、-1 600万元、200万元、100万元。试计算该项目的内部收益率。

1.IRR函数法。若按前面常规项目的求解过程操作，得出的解为5.80%，但实际上该现金流序列存在两个解：5.80%、17.01%。IRR函数之所以不能求出所有的解是因为它求出IRR的一个解后就返回结果停止工作，IRR函数的原型为IRR（Values，[Guess]），其中Guess是对IRR结果的估计值，默认值为0.01，Excel使用迭代法计算，从Guess=0.01开始，不断修正计算结果，找到解后停止；如果IRR运算20次，仍未找到结果，则返回错误值#NUM！。在例2中若要找到另一个解就要改变Guess值，具体步骤为：在IRR函数中加入参数Guess，将其值从0.01开始逐渐递加，当加到0.12时，IRR的值变为17.01%，此为IRR的第二个解。

2.单变量求解法。在单变量求解法中，具体步骤为：求出第一个解5.80%后，改变A1单元格的初始值为1，再执行单变量求解法的第二个步骤，求得IRR为17.01%。因为Excel中的单变量求解，只能得出一解，可以通过改变可变单元格的初始值找到另外的解，可变单元格的初始值在使内含报酬率的值有意义的区间：0—1范围内改变。

三、内含报酬率多解问题分析

同时出现多个内含报酬率的投资方案，必定是非常规方案，但并不是每一个非常规方案都会同时出现多个内含报酬率。按照财务管理的理论，如果有一个方案出现了多个IRR而不能排除，则内含报酬率不再适用于该投资方案的评价，因此遇到这种情况时有效进行IRR的排除是投资决策中关键的程序。

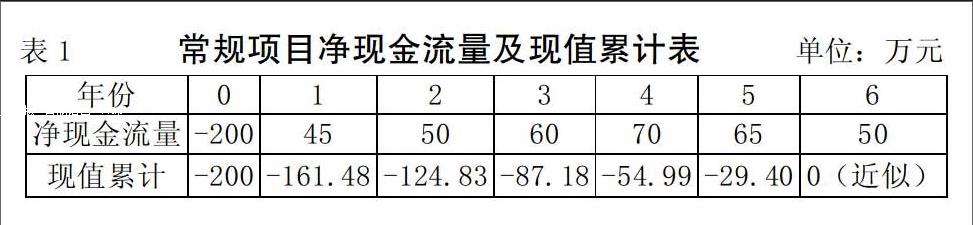
（一）多解问题的排除原理。通过计算得出的IRR都符合其定义，但是它们并不一定符合内含报酬率的经济内涵。在非常规项目中应用内含报酬率的公式计算时实际上隐含了再投资假设，再投资假设解决的是若存在再投资机会，公司利用较早获得的现金流入量进行再投资，其投资报酬率至少是多少的问题。观察内含报酬率的公式很容易看出它所假设的再投资报酬率为内含报酬率，这样，内含报酬率法按照内含报酬率评估再投资机会，但实际上这种做法欠妥，非常规项目的净现金流出现负值很可能是由分期投资或滚动投资造成的，此时合理的贴现率应该是资本成本。在常规项目中，只存在一个内含报酬率，除了初始投资的净现金流为负，以后各年现金流符号都为正，投资是在整个投资年限末才收回的，因此不存在再投资假设。对例1来说，其投资回收期内现值累计变化计算如表1，在16.81%的内含报酬率下，初始投资在1—5年都存在未收回的金额，只有在项目投资期末才完全收回，不存在再投资问题。

笔者认为，要使非常规项目的内含报酬率能客观评价该项目，就要去除内含报酬率计算过程中所隐含的不合理的再投资假设对结果的影响，使投资项目中不存在再投资收益率问题，在非常规项目存在多个内部收益率时根据下述规则进行排除：按合理的IRR计算，投资项目在整个寿命期内必须始终处于投资回收状态，各年均存在未收回投资额。也就是说，使投资回收期内出现正的累计现值的内含报酬率应该被排除掉。当非常规投资项目有多个正实数根时，须经过检验，符合经济涵义的根才是项目的内部收益率；如果只有一个正实数根，同样需要检验。

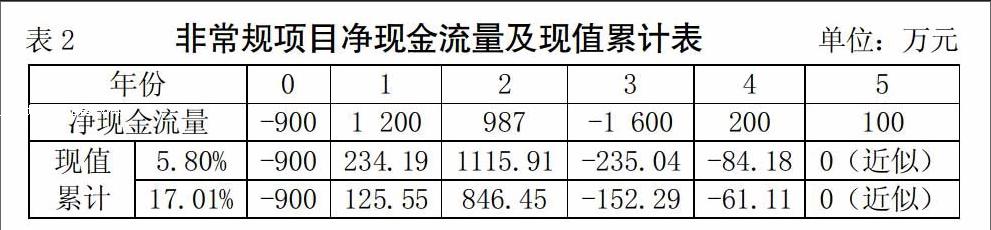
（二）排除决策举例。依然沿用例2，根据两个内含报酬率：5.80%、17.01%计算出的投资回收期内各年累计现值变化如表2，可以看出投资项目并非始终处于未回收状态，而是在第1年和第2年出现了局部盈余，现值累计为正值，与上述规则不符，所以5.80%和17.01%不符合投资项目内部收益率的经济涵义，可以排除。

四、结论

对于常规项目，运用Excel中的IRR函数法或单变量求解法即可准确简便地求出内含报酬率；对于非常规项目，仍可在两种方法的基础上稍作改动求出它的多个解：IRR函数法通过不断修改Guess值求出多解，单变量求解法通过改变可变单元格的初始值求出多解。但是，用Excel求出的非常规项目的一个或多个IRR不一定符合内含报酬率的经济内涵，应该去除不合理假设的再投资报酬率的影响，根据各年的现值累计有效地进行排除。

参考文献：

[1]叶璋礼.基于年金特征的内部收益率速算研究[J].商业会计，2014，（08）：76-78.

[2]李萍.利用Excel函数功能计算净现值和内含报酬率[J].当代会计，2014，（02）：38-40.

[3]刘姝蕙，陈锦辉.运用二分法求解内含报酬率[J].财会月刊，2012，（26）：52.

[4]马良渝.求解IRR的多个解的Excel方法[J].中国管理信息化，2005，（10）：20.