土石坝渗透破坏影响因素分析

范伟，张宏博

（1.山东水总有限公司，山东济南250014；2.山东大学土建与水利学院，山东济南250061）

土石坝渗透破坏影响因素分析

范伟1，张宏博2

（1.山东水总有限公司，山东济南250014；2.山东大学土建与水利学院，山东济南250061）

依托卧虎山水库工程实例，采用Galerkin有限元方法针对稳定与非稳定渗流两种情况，分析了心墙渗透系数、上下游水位、心墙坡度、水位突变等各参数对土石坝渗透破坏的影响，建立了土石坝渗透坡降的功能函数，并确定了功能函数随各参数的概率分布。

渗透破坏；渗透系数；水位；功能函数；概率分布

本文依托卧虎山水库的工程实例，采用不变网格法中求解自由面渗流问题的截止负压法进行渗流计算，直接以压力场为未知函数，利用Galerkin有限元方法并结合固定网格迭代来确定自由面，详细阐述了坝体渗透性能随心墙渗透系数、上下游水位、不同坝体壤土、水位突变等参数的变化规律和概率分布。

1　卧虎山水库渗透破坏分析

2　土石坝渗流稳定性分析

2.1计算模型的建立

根据调查分析，济南周边水库多为中小型土石坝，主要为心墙坝及均质坝，坝高多在10～40 m。假定坝高40 m，建立心墙土石坝有限元力学模型。

2.2计算参数的选取及计算流程

根据济南市卧虎山水库地质勘查报告，确定土石坝渗流计算物理力学参数如表1所示。

表1　土石坝渗流计算物理力学参数表

根据济南市卧虎山水库地质勘查报告及卧虎山水库运营资料统计，确定土石坝渗流计算物理力学参数如表2所示。

计算流程如下：首先采用理正岩土渗流计算模块，分析心墙渗透坡降分布规律，确定最大渗透坡降；然后计算渗透坡降功能函数，拟合功能函数表达式；再采用概率论知识，拟定参数的概率密度函数，进行功能函数的概率求解。

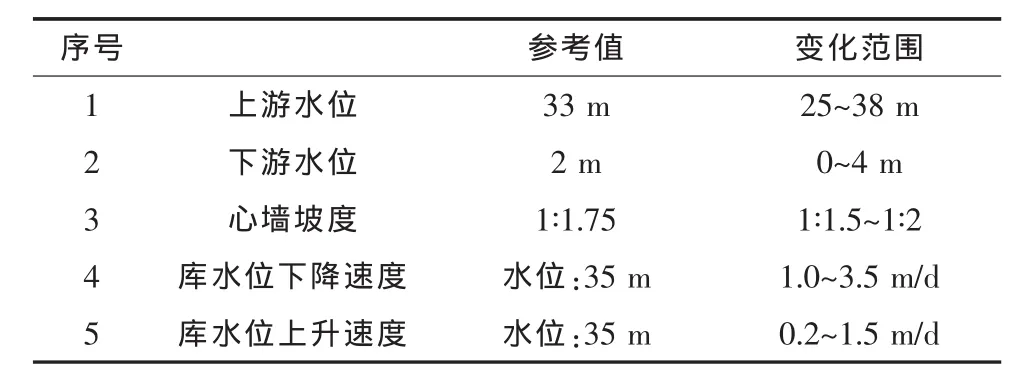
表2　土石坝渗流计算工况参数表

2.3稳定渗流计算结果

因变异参数较多，以黏土心墙渗透系数变化为例进行说明。

1.开发利用档案，给企业带来明显的经济效益。徐州发电有限公司从1994年开始探讨对4台125MW和4台200MW机组全面改造方案，公司综合档案科提供了汽轮机、发电机、锅炉及其辅助设备总图等大量有参考价值的科技档案，利用科技档案卷次共800余卷，从1997年至2001年，先后对8台机组进行了现代化技术改造，改造后的机组各项经济技术指标，达到了国内同类型机组的先进水平。通过技术改造，不仅延长了机组的寿命，使老机组焕发了青春，而且大大提高了机组安全可靠性、可控性、可调性和自动化水平，增强了企业实力，对于企业参与市场竞争，迎接新世纪挑战，无疑具有重大的现实意义和深远的历史意义。

经计算，随着心墙渗透系数的增大，浸润线的位置逐渐降低。根据计算结果绘制心墙、坝前及坝后最大坡降功能函数值（J（X）=Jcr-J）与心墙渗透系数的关系曲线，如图1所示。

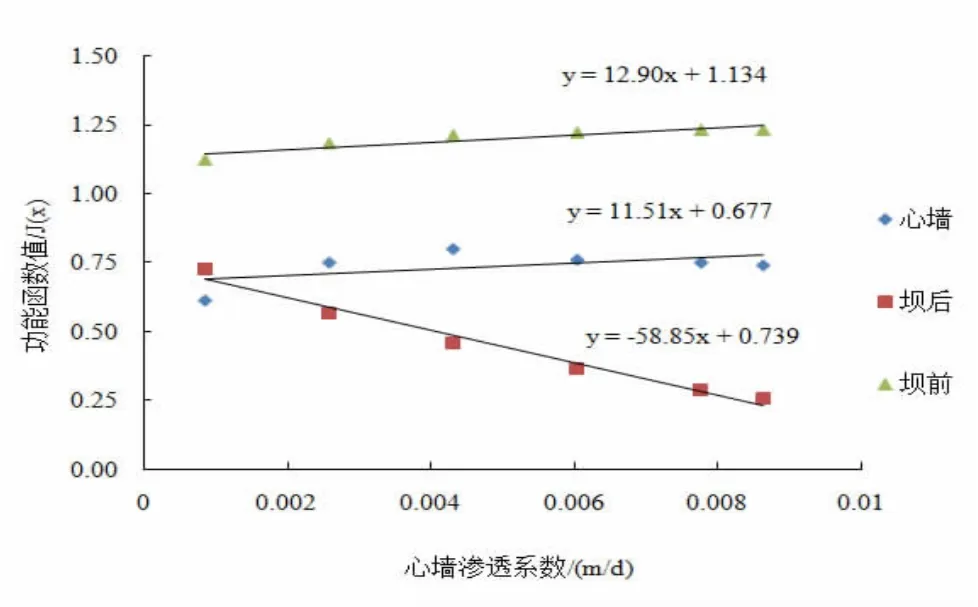
图1　不同心墙渗透系数时渗透功能函数变化规律

由图1可知，随着黏土心墙渗透系数的增大，坝前坡及心墙坡降变化幅度较小，坝后坡的坡降值变化最为明显，更接近于临界坡降值，表明坝后坡更容易发生渗透破坏。

同理，可得到心墙坡度、上、下游不同水位（如图2所示）、坝体壤土渗透系数等不同条件下坝前（图省略）、心墙及坝后最大坡降变化规律（图省略）。

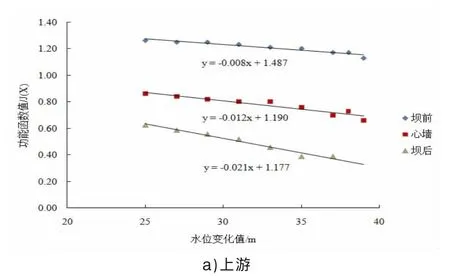
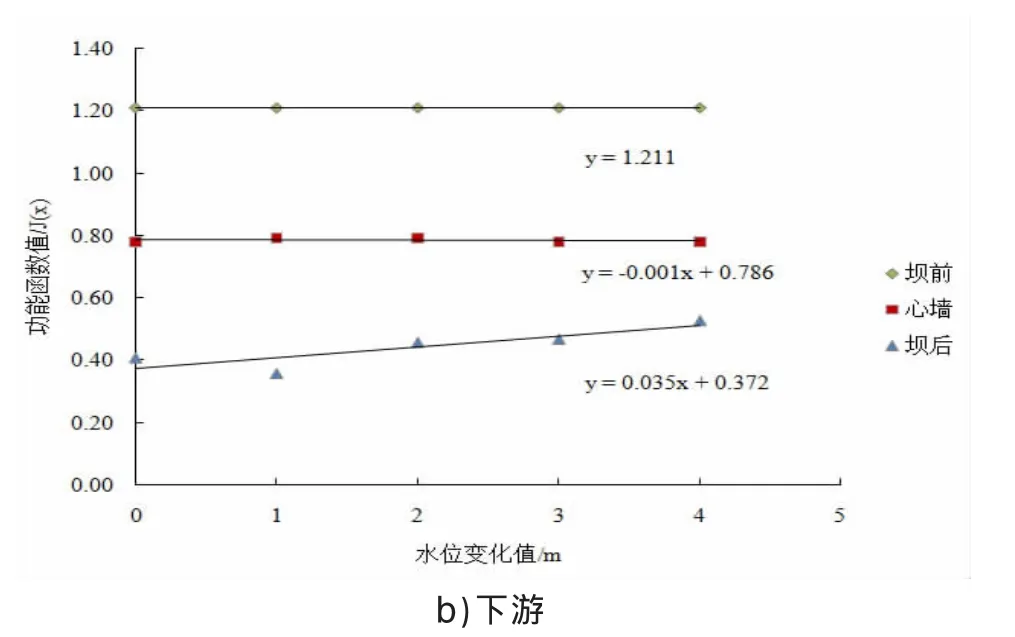
图2　上、下游水位变化的影响

对比图2上下游水位变化，上游水位增高，坝前坡、心墙及坝后坡坡降均明显增大，破坏函数明显呈降低趋势，表明破坏概率增加幅度较大。而下游水位抬高，仅对坝后坡坡降略有影响。

坝后坡壤土渗透系数增大，坡降破坏函数值增加，表明坝后坡渗透破坏概率减小；但心墙位置坡降破坏函数值降低，表明坝体内部承受渗透压力更大，破坏概率增大。

心墙坡度对坡降的影响不显著，所以在保证心墙施工和运营安全的情况下，心墙下部可适当缩减尺寸。

2.4非稳定渗流计算结果

考虑库水位突升和突降，计算非稳定渗流条件下坝体渗透坡降变化。选取坝前、心墙和坝后渗透坡降最大值，绘制渗透破坏函数与水位突升和突降的关系曲线。

由关系曲线可知，坝后坡渗透破坏函数值最小，表明此处更易发生渗透破坏。随着水位突降速率的增加，心墙的渗透破坏函数衰减趋势相对较为明显，表明水位突降对心墙的渗透稳定影响最大。水位快速上升对坝体渗透稳定影响更为显著，特别是坝前和心墙渗透破坏函数明显衰减，当水位上升速度超过1.0 m/d时，心墙渗透破坏功能函数衰减至0以下，表明心墙将发生渗透破坏。

3　坝体渗透破坏概率分布求解

根据相关文献资料及卧虎山水库地勘资料及运营资料，拟定变量数学期望值及方差。并根据前述确定的渗透破坏功能函数，确定渗透破坏分布函数的数学期望和方差，如表3所示。

根据上表中所确定的数学期望和方差，采用excel表格中的数学函数Normdist函数，绘制渗透破坏正态分布函数，并求解破

表3渗透破坏分布函数表

变量名称变量分布函数渗透破坏功能函数因子渗透坡降破坏分布函数ab位置参数心墙渗透系数0.0055m/d5E－6－58.850.7390.4151.73E－02上游水位33m10.56－0.0211.1770.4844.66E－03库水位上升速度0.75 m/d0.14－0.5880.7030.2624.84E－02

坏概率。基于上述分析，重点针对心墙渗透系数、上游水位和库水位上升速度3种变量因素进行分析。

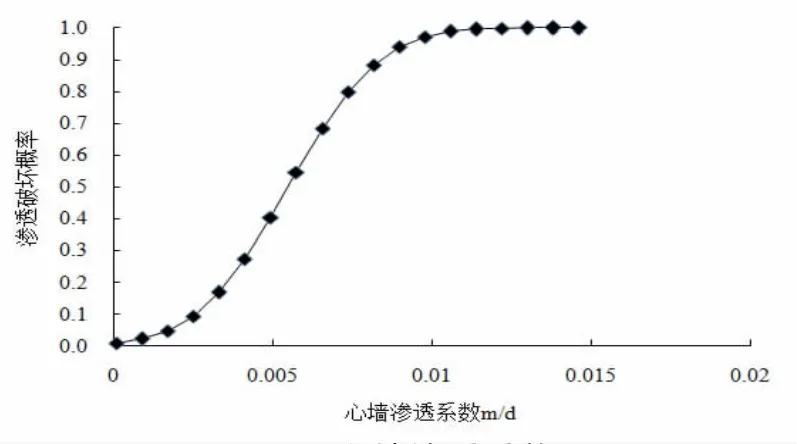
图3　心墙渗透系数

由图3可知，随着心墙渗透系数增加，坝体渗透破坏概率逐渐增加，当心墙渗透系数增至0.01 m/d时，坝后坡渗透破坏概率接近100%。为了保证坝体安全，建议心墙渗透系数应不大于7E－06 cm/s。

随着上游水位的不断抬高，坝后坡的破坏概率迅速增加，当水位抬升至40 m（漫顶水位）时，坝后坡渗透破坏概率为100%。因此，为了保证坝体安全，库水位建议控制在35 m以下。

水位上升速度越快，对心墙渗透稳定性影响越大。因此，为了保证心墙安全，水位上升速率应控制在1.0 m/d以内。

4　结语

1）心墙渗透系数大、上游水位高，土石坝更易发生渗透破坏，而心墙坡度对水力坡降影响不显著。

2）从非稳定渗流功能函数中可以看出：水位突升突降对心墙稳定性影响较大。

3）土石坝渗透破坏功能函数与心墙渗透系数、上游水位、水位突升速度符合正态分布，为了保证坝体安全，建议心墙渗透系数应不大于7E－06 cm/s，库水位控制在35 m以下，水位上升速率应控制在1.0 m/d以内。

［1］王栋，朱元甡．防洪系统风险分析的研究评述［J］．水文，2003，23（02）：15－20.

［2］朱元甡．上海防洪（潮）安全风险分析和管理［J］．水利学报，2002，（08）：21－28）.

（责任编辑迟明春）

TV698

B

1009-6159（2016）-09-0001-02

2016-05-15

范伟（1977—），男，高级工程师