级联型高压变频器输出电压观测器研究与实现

胡志涛，李兴鹤

（1.上海新时达电气股份有限公司，上海201802；2.上海辛格林纳新时达电机有限公司，上海201802）

级联型高压变频器输出电压观测器研究与实现

胡志涛1，李兴鹤2

（1.上海新时达电气股份有限公司，上海201802；2.上海辛格林纳新时达电机有限公司，上海201802）

首先介绍了级联型高压变频器系统（CAS-HVI）拓扑结构；然后针对级联型拓扑结构，结合载波移相调试算法，引出了基于直接转矩控制的高压变频器系统（HVI-DTC）对输出电压的观测（重构）需求；再着重就载波移相对输出电压重构的影响进行分析，并分别对传统DTC与SVM-DTC控制的输出电压重构进行研究；最后在样机上实现重构算法，并分析实验结果，结果验证了重构效果及必要性。

级联高压变频器；载波移相；直接转矩控制；电压重构

引言

随着电气传动技术和变频调速技术的发展，以及开关器件不断的更新换代，体现高压大功率变频调速技术的高压变频器也越来越多地被学者和研发人员关注，其中以级联型拓扑结构且采用载波移相调制为代表的高压变频器已经逐渐成为高压变频器的主流结构［1］。但是传统高压变频器基本不会考虑载波移相的影响，因此会对输出电压的观测、死区补偿的效果，甚至高性能的控制性能产生一定影响，因此传统高压变频器基本只能采用VFFF标量控制，并且很少有计算输出有功和功率因素，即使计算精度也不会很高；而随着高压变频器应用到越来越多的行业，不仅对其运行的稳定性以及长时间不间断工作提出了高要求，同时也对转速的控制精度、转矩的快速响应提出更高要求，如在密炼机、轧钢机行业的应用。对于大功率风机、水泵的变频调速有很好效果的VFFF标量控制算法，此时就很难满足要求，由此推出了基于转子磁场定向控制的高性能高压变频器［2］，以及对转矩响应更快的DTC高性能高压变频器。这些控制算法就要求对级联型高压变频器有更精确和更细节的分析与研究。对于DTC控制算法而言，对输出电压的检测或重构的精度会直接影响到磁链观测的结果，进而影响控制效果，另外，通过瞬时输出功率方法的计算输出功率时，会受到输出电压重构精度的影响，同样会影响功率因数的计算，也会影响诸如同步电机功率因数为1的控制效果。

对此，本文从级联型高压变频器的拓扑结构及调制方式的原理入手，推导输出电压的重构方法，并通过实验方法，定量分析不考虑载波移相的作用而产生的影响，以及验证重构方法的效果。

1　级联型高压变频器系统

1.1级联型高压变频器系统拓扑结构与功率单元结构

考虑开关器件的耐压、谐波及du/dt，市场上高压变频器多采用级联型的拓扑结构。这类系统通常由移相变压器、功率单元组、主控系统、光纤通信系统、输入输出侧电流采集模块以及IO、通信模块和人机界面等8大模块组成［3］。6 kV进线高压通过移相变压器分别为15个功率单元提供690 V输入电压，所有功率单元均由主控系统通过光纤进行集中控制，15个功率单元分为3组，每组5个单元上下串联共同作用产生一相输出，其系统拓扑结构示意如图1所示。所有单元都正常工作时，A、B、C三相输出电压动态平衡，输出相电压约为3 450 V，输出线电压约为6 000 V。

在级联型高压变频器系统中，功率单元是最为核心的部件，甚至可以将其看作是一个独立变频器。输入是三相交流电压（多为690 V），输出是单相交流电压（多为690 V）。级联型高压变频器载波移相调试算法与功率单元的结构密切相关。图2为功率单元结构，其由不可控整流桥、母线电容、均压电阻以及开关器件组成，其中4个开关器件（Q1～ Q4）构成H桥结构，分别是左上桥（即Q1）、左下桥（即Q2），右上桥（即Q3）、右下桥（即Q4）。

每个功率单元都有4路PWM驱动信号控制H桥的4个桥臂（IGBT）的开关动作。该调制算法下，4路PWM是互相关联，如果已知其中1个桥臂状态，就能推出其他3个桥臂状态。比如不考虑死区，左上桥占空比80%，左下桥为相反状态20%，右上桥与左上桥中心对称，占空比为100%-80%=20%，右下桥与右上桥互为相反状态，其波形示意如图3所示。

图1　5级联高压变频器系统拓扑结构Fig.1 High-voltage inverter system cascaded topology

图2　高压变频器功率单元结构Fig.2 Power unit structure

图3　H桥4桥臂PWM波形示意Fig.3 Sketch map of PWM waveforms of H-bridge four-leg

1.2级联型高压变频器调制算法

载波移相调制算法非常适用于多电平逆变器，不但能够降低du/dt，还能减少输出的电压谐波［4-5］，因此，级联型高压变频器较多采用该调制算法。具体而言，可选择SPWM载波移相调制CPS-SPWM（carrier phase shifting SPWM）及SAPWM载波移相调制CPS-SAPWM（carrier phase shifting SAPWM）、SVPWM载波移相调制（CPS-SVPWM）算法等。以CPS-SPWM为例说明其基本原理。对于由n个H桥功率单元组成的单相级联多电平变频器，所有功率单元都采用SPWM调制算法，每个功率单元的正弦调制波都相同，然后对n组三角载波分别进行调制，每组三角载波都具有相同的频率及幅值，但每组三角载波的相位依次相差固定的相角，从而使每个功率单元输出的SPWM电压脉冲也相应错开一定的角度，从而大大增加了等效开关频率（因此可以采用较低三角载波频率进行调制），经过电压的串联叠加，变频器最终输出电压的波形是一个具有2n+1个电平的阶梯波，而且通过选择合适的移相角度（如T/（2n）或T/n）还可以更进一步降低输出电压谐波含量［5］，如图4所示，为理想情况5级联输出的电压波形，固定移相角度为T/10（其中T为载波周期）。

图4　CPS-SPWM输出的电压波形Fig.4 The output voltage waveforms of the CPS-SPWM

1.3CPS对电压重构的影响

许多高性能电机驱动算法，如DTC控制算法等［6-8］，常用磁链转矩观测器的构建模型为

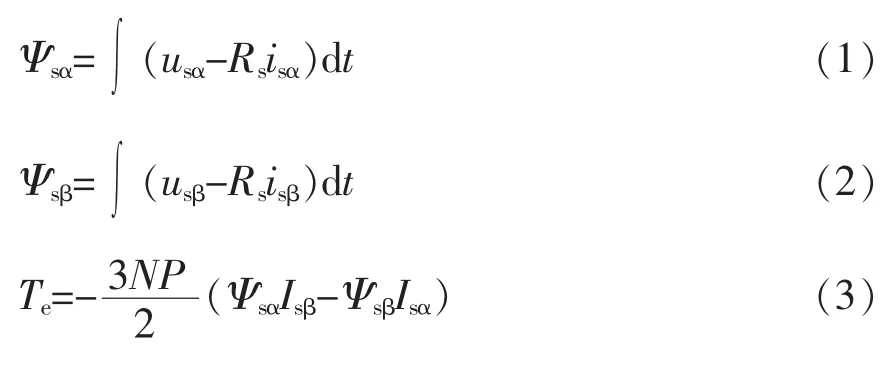
其中输出电压的检测是关键之一，如果直接通过传感器实时检测输出电压，称之为直接法，但是很多情况下可能没有使用输出电压传感器，这样就需要采用间接的方式来重构。

针对级联型高压变频器拓扑结构，可在直接转矩控制算法输出的PWM基础上，加入载波移相调制算法［6-7］。如将开关矢量产生驱动A相功率单元左上桥开关器件的PWM信号作为原始信号PWM 1；然后分别右移角度δ、2δ、3δ、4δ，对应生成PWM2～PWM5，其中可选取δ=T/（2Ns），（Ns为级联数，要求0＜δ＜T/Ns），左上桥PWM移相示意如图5所示。PWM1～PWM5可以随机对应A相功率单元1～5的左上桥，当每个功率单元左上桥PWM信号确定后，剩下的三路PWM信号也随之确定。

因此，经过载波移相后A相5个功率单元级联输出的电压效果如图6所示。可以发现经过移相处理后，周期k中存在部分PWM移入周期k+1中（如PWM3～5），同时周期k-1中存在部分PWM移入周期k中。由此可见，由于移相调试，使得当前输出电压不能直接简单由PWM的占空比进行估算。

图5　左上桥PWM移相示意Fig.5 PWM phase shift diagram of the upper bridge

图6　脉宽可调时输出的PWM波形Fig.6 PWM waveforms of pulse width adjustable

2　输出电压重构方法

2.1DTC调制电压重构

传统DTC调制方式，是整个周期全开或全关。A、B、C三相功率单元母线电压之和分别为

式中：Ua、Ub、Uc分别为所有正常工作的A、B、C相单元母线电压之和（如果出现单元旁路，则被旁路单元母线电压不计入其中）；UdcAi、UdcBi、UdcCi分别为对应功率单元Ai、Bi、Ci的母线电压；enAi、enBi、enCi分别为对应功率单元工作状态，0表示被旁路，1表示正常工作；ccra、ccrb、ccrc分别为A、B、C相占空比。

假设移相比例为x，T为满周期，简化计算移相部分。移至下一开关周期的部分可表示为

式中：x为移相部分所占开关周期的比例，x≤1/（Ns-1）。因此PH最大值为

则第N个开关周期输出电压为

式中：U（N）为第N个开关周期的输出电压；Uccr（N）为第N个开关周期程序给出PWM开关指令，如全开为1、全关为-1（“1”与“-1”的选择与级联的方式有关，参考“7根据中性点位置自动调整开关矢量）；Udc（N）为第N个开关周期该相的母线电压和，如A相母线电压和：，其中UpuAi表示功率单元Ai的母线电压。

2.2SVM-DTC调制电压重构

近些年不少学者将SVM调制策略融入到DTC控制中，形成SVM-DTC控制策略，该调制策略需要脉宽可调。因此有必要分析研究脉宽可调情况下的电压重构技术。

假设不考虑死区影响，脉宽通过标幺化处理，脉宽0～1，全开为1、全关为0（“1”与“0”的选择与级联的方式有关）输出电压。首先三相输出电压中每一相计算方法相同。以A相举例，如图6，其中ccr1k表示第k个开关周期，左上桥臂PWM宽度；ccr3k表示第k个开关周期，右上桥臂PWM宽度；ccr1k-1表示第k-1个开关周期，左上桥臂PWM宽度；ccr3k-1表示第k-1个开关周期，右上桥臂PWM宽度。

图中存在2个输出电压概念：①在第k个周期内实际输出电压，图6中虚线矩形框内阴影部分，定义为Uok；②在第k个周期软件确定输出PWM后，其具体输出电压的时间分布（需要理解在第k个开关周期输出PWM经过载波移相输出电压的结果），图6中虚线菱形框内阴影部分，定义为Uk。

由图6可以看出，Uk可能部分处于周期k+1中，故令

式中：Uk1为周期k内的电压；Uk2为由于移相作用而被移到周期k+1内的电压。

因为ccr1k、ccr3k均已知，有

式中，Udci为该相上第i个功率单元母线电压。

为减少计算，假设所有功率单元母线电压相同，即为Udc，则式（6）可简化为

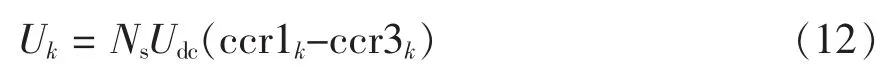
显然在第k个周期内实际输出电压为

式中，U（k-1）2为第k-1个周期PWM由于移相作用而被移到周期k内的电压部分。

因此关键就是计算Uk2，U（k-1）2的计算方法与Uk2相同。计算得出Uk2、U（k-1）2后，则

因为输出有效电压是ccr1k与ccr3k共同作用的结果，简单说就是（ccr1k-ccr3k），为了计算方便，将ccr1k与ccr3k的作用分别独立计算。令ccr1k因移相作用移到周期k+1内对应的输出电压为Uk2a，ccr3k因移相作用移到周期k+1内对应的输出电压为Uk2b，则

假定移相调制中，则有

式中：T为开关周期；ps为移相时间。进行标幺化处理，将T设定为1，则ps表示周期的百分比。

分两种情况讨论并分别计算Uk2a、Uk2b。

（1）ccr1k＞50%

独立分析ccr1k，即可得出Uk2a为

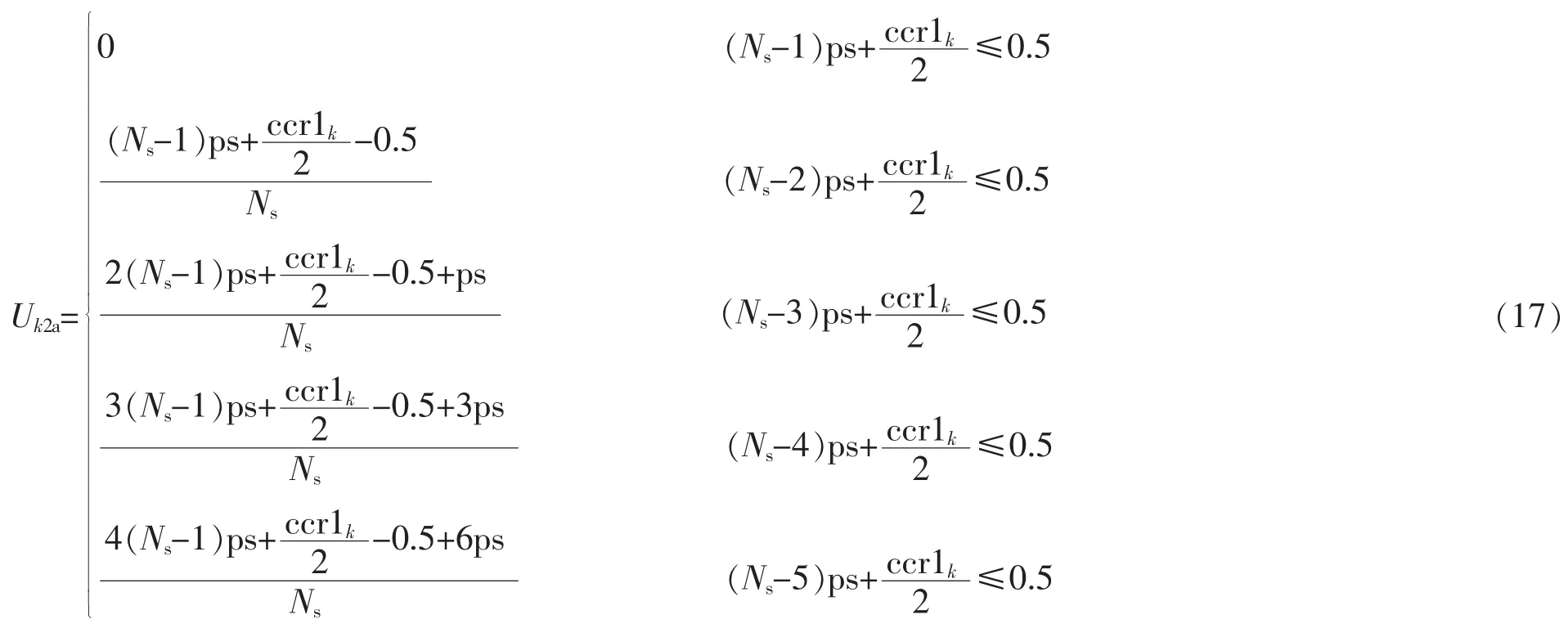
其中，m作为对式（18）条件的抽象，可以理解为移相编号（编号0表示没有移相，编号1表示移相ps，编号2表示移相2ps，依此类推，编号m表示移相mps，因此m最大值为Ns-1，对于五级联高压变频器来说m最大为4。

独立分析ccr3k，即可得出Uk2b为

（2）ccr1＜50%，即ccr3＞50%

采用相同分析方法，独立分析ccr1k，即可得出Uk2a为

独立分析ccr3k，即可得出Uk2b为

其中，s与m同理作为对上述公式条件的抽象，可以按照与m相同的意思进行理解。

可以发现，Uk2a和Uk2b的表达式在ccr1k＞50%情况下与ccr1k＜50%情况下完全一样，因此可以将两种情况合二为一。但是需要注意：ccr1k＞50%情况下，Uk2a＞Uk2b，即Uk2＞0；而ccr1k＜50%情况下，Uk2a＜Uk2b，即Uk2＜0。

3　实验验证

为验证第2.2节方法的有效性，采用公司现有的实验平台，如图7所示。其中，高压变频器实验用机为新时达AS800 800 kW高压变频器，其主要包括移相变压器柜、控制柜和逆变器柜，可支持标量控制和矢量控制。为验证输出电压的重构效果，该高压变频器系统加上硬件电压检测电路（该检测电路带宽为10 kHz），模拟量输出接口可以同时实时输出硬件检测的输出电压以及重构的输出电压。560 kW高压异步电机实验平台如图8所示，其中，电机1作为被试电机（电机2是对拖负载电机，本实验中不用）。

图7　新时达AS800高压变频器Fig.7 High voltage inverter of STEP AS800

图8　电机测试平台Fig.8 Experimental test platform of moter

实验测试波形如图9～图12所示。图中上半部分为下方椭圆内的放大图形。图中下半部分虚线左边表示不考虑移相移相影响，直接重构出的输出电压波形；虚线右边表示考虑移相影响，采用式（18）～式（25）重构出的电压。

图9　50Hz CPS-SPWM输出电压重构效果对比Fig.9 Effect comparison of CPS-SPWM output voltage at 50 Hz

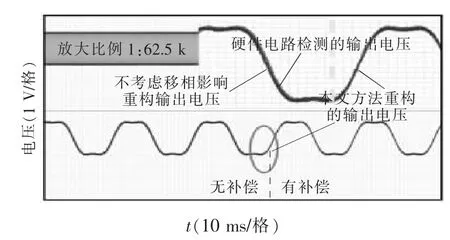
图10　50Hz CPS-SVPWM输出电压重构效果对比Fig.10 Effect comparison of CPS-SVPWM output voltage at 50 Hz

图11　25 Hz CPS-SPWM输出电压重构效果对比Fig.11 Effect comparison of CPS-SPWM output voltage at 25 Hz

图12　25 Hz CPS-SVPWM输出电压重构效果对比Fig.12 Effect comparison of CPS-SVPWM output voltage at 25 Hz

通过图9～图12实验对比，可得如下结论：

（1）不考虑移相影响直接重构出的输出电压要超前于实际输出电压约0.33 ms；

（2）采用本文提出的重构算法重构出的输出电压与实际电压基本重叠，可以认为延时小于0.1 ms，且在高频时也有很好的重构效果；

（3）本文提出的重构算法分别在SPWM、SVPWM两种载波移相调制算法下的实验结果相似，可以认为不受调制算法影响；

（4）输出频率越高时，不加补偿重构电压的误差就越明显。

依据实验结果，可以推算出大致相位差。50 Hz时，不考虑移相影响直接重构出的电压超前大致0.33 ms，则超前角度：ε=360°×（1/3）/20=6°，对三角函数运算（诸如功率因素计算等）的影响为0.55%～10.45%。25 Hz时，不考虑移相影响直接重构出的电压超前大致0.33 ms，则超前角度：ε=360°×（1/3）/ 40=3°，则对三角函数运算（诸如功率因素计算等）的影响为0.28%～5.28%。由此可见移相调制在某些情况下，对控制还是有较大影响。

4　结语

由于级联型高压变频器传统的标量控制技术已经越来越多的无法满足现场需求，越来越多的学者及工程技术人员开始研究在该拓扑结构下实现转矩响应性能更快、控制性能更高的矢量控制或直接转矩控制，在这样的背景下，本文就高压变频器的输出电压重构展开研究，分析出级联型拓扑结构下移相调制算法对输出电压的影响，分别探讨传统DTC与SVM-DTC控制的输出电压重构，并在小样机上针对CPS-SPWM与CPS-SVPWM调试算法在不同频率下进行验证。实验结果验证了重构算法可以适用于不同的移相调制算法，且重构电压与硬件直接检测的电压的效果相近，明显提升了传统观测的精度，进而提升可提升磁链观测、功率因素计算的角度，也为高性能矢量控制以及直接转矩控制的后续研究工作提供帮助。

致谢：本文中实验方案的制定和实验数据的测量记录工作是在上海新时达电气股份有限公司金辛海、宋吉波、张震宇、吴芸等工作人员的大力支持下完成的，在此向他（她）们表示衷心的感谢。

［1］北京中讯国际信息咨询中心.2009-2012年中国高压变频器行业市场分析研究及预测报告［R］.2013. BeijingZhongxunInternationalInformationConsulting Center.2009-2012 Chinese high voltage inverter market analysis and forecast report［R］.2013（in Chinese）.

［2］上海辛格林纳新时达电机有限公司.新时达AS800 V系列高压变频器说明书［M］.2010：10-12.

［3］上海辛格林纳新时达电机有限公司.新时达AS800 E系列高压变频器说明书［M］.2012：31-35.

［4］刘凤君.多电平逆变技术及其应用［M］.北京：机械工业出版社，2007.

［5］李彬彬，周少泽，徐殿国.模块化多电平变换器与级联H桥变换器在中高压变频器应用中的对比研究［J］.电源学报，2015，13（6）：9-17. Li Binbin，Zhou Shaoze，Xu Dianguo.Comparative study about application of modular multilevel converter and cascaded h-bridge in medium-high voltage converter［J］. Journal of Power Supply，2015，13（6）：9-17（in Chinese）.

［6］Depenbrock M.Direct self-contro（DSC）of inverter-fed induction machine［J］.IEEE Transactions on Industrial Elec

Study and Implementation of Output Voltage Observer for Cascaded High Voltage Inverter

HU Zhitao1，LI Xinghe2
（1.Shanghai STEP Electric Co.，Ltd.，Shanghai 201802，China；2.Shanghai Sigriner STEP Electric Co.，Ltd.，Shanghai 201802，China）

Firstly，the system topology of cascaded high voltage inverter（CAS-HVI）is introduced in this paper. Secondly，according to the topological structure of the cascade and combined with carrier phase shifting algorithm debugging，the output voltage observation requirements on high voltage inverter system HVI-DTC has been drawn based on direct torque control.Then，the impact on heavy carrier shift relative to the output voltage observation respectively is analyzed，and the traditional DTC and SVM-DTC control of output voltage observation research is studied.Finally，the observation algorithm achieves in the prototype and the observation effect and the necessity is validated.

cascade-type high-voltage inverter；carrier phase shifting；direct torque control；voltage observation

胡志涛

10.13234/j.issn.2095-2805.2016.5.137

TM 464

A

胡志涛（1974-），男，通信作者，硕士，主要从事电梯控制技术、电力电子技术、机器人智能控制相关领域的研究与管理工作，E-mail：huzt@stepelevator.com。

李兴鹤（1981-）男，硕士，高级工程师，研究方向：自动控制技术、电力电子技术、嵌入式技术，E-mail：lixinghe_learn@ 126.com。

2015-12-01

国家科技支撑计划资助项目（2014BAF08B05）

Project Supported by National Science and Technology Support Plan（2014BAF08B05）