基于时间逼近搜索算法的城轨列车运行节能优化研究
(西南交通大学电气工程学院,四川成都610031)
(西南交通大学电气工程学院,四川成都610031)
针对地铁列车准点节能运行,提出了基于时间逼近搜索的列车节能优化算法.首先建立城市轨道列车在满足定时运行条件下的节能控制模型,通过庞特利亚金最大值原理得到了列车节能最优控制工况集;其次,推导了列车在不同节能运行模式下的能耗差异;在此基础上,提出了一种将列车运行区间进行分段优化的方法,采用时间逼近搜索求解列车工况转换点的位置,最终达到定时节能运行的目的.以上海地铁3号线铁力路至友谊路线路为算例,与实测负荷过程对比,列车采用本文算法优化后可节能12.5%.
城市轨道;节能控制;时间逼近;优化
随着城市轨道交通的迅速发展,列车运行能耗正逐步受到人们的关注,研究列车在满足运行时分的条件下更加节能地运行对降低运营成本和促进低碳经济具有重要的意义[1].
关于城市轨道交通列车运行优化问题国内外做了很多研究.国外方面,文献[2]采用极大值原理求解列车节能驾驶策略,并最终采用数值算法求解转换点,但因涉及到复杂的数学解析计算,求解过程较为繁琐;文献[3-4]采用基因算法、蚁群算法和动态规划算法求得速度曲线,虽然节能效果好,但是计算时间较长;文献[5-7]采用人工神经网络求解列车节能优化控制问题,但人工神经网络训练数据的好坏会直接影响优化结果;文献[8]将进化算法应用到列车速度曲线优化的问题中,但是实现起来较为困难,也不利于快速收敛到最优解.国内方面,文献[9]给出了节能坡纵断面的竖曲线设计方法,节能坡和列车动力配置相结合,可实现系统优化配置,但在已经建设完成的线路中该方法难以适用;文献[10-11]中采用了自适应遗传算法,虽然节能效果明显,但要求的站间距相对较长,不适用于站间距相对较短的城市轨道交通;文献[12]提出了一种变长实矩阵编码的多种群遗传算法,增强了算法的全局搜索能力,但在限速复杂的情况下,难以求得最优解.
本文从数学解析计算的角度对比了列车在定时运行条件下不同节能操纵策略对应的牵引能耗.根据列车节能操纵的原则,设计了一种将列车运行区间进行分段优化的方法,通过时间逼近来搜索待优化区间,调整列车运行工况,从而实现列车定时节能运行的目的.
1 城市轨道列车最优控制模型
城市轨道列车优化运行问题的实质是列车在给定运行时间和运行距离条件下,能耗最低.其节能优化的目标函数如式(1)[12]:
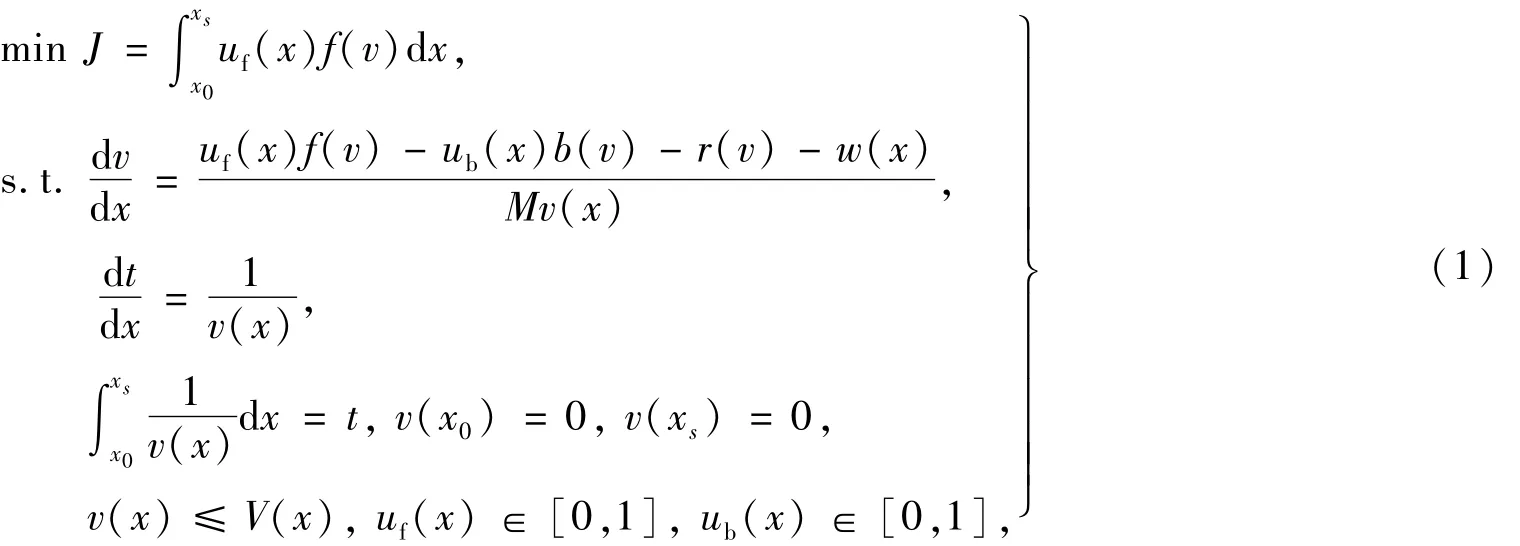
式中:J为牵引力做功的机械能耗,简称牵引力能耗;uf(x)为牵引力使用系数;ub(x)为制动力使用系数;f(v)为列车在速度v下的最大牵引力(由牵引力特性曲线决定);b(v)为列车在速度v下的最大制动力(由制动力特性曲线决定);M为列车的总质量;v(x)为列车在位置x处的速度;V(x)为列车在位置x处对应的限速;t为给定的列车运行时间;r(v)为列车运行基本阻力,如式(2)所示;w(x)为列车在位置处对应的加算坡道阻力,如式(3)所示[13].

式中:a、b、c为基本阻力公式系数,一般由车辆自身特性决定.
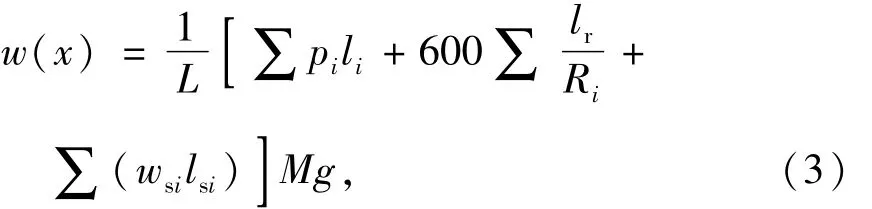
式中:L为列车长度;pi、li分别为列车所覆盖的第i个坡道的千分数和长度;Ri、lr分别为列车所覆盖的第i个曲线的半径和长度;wsi、lsi分别为列车所覆盖的第i个隧道的单位隧道阻力和长度.
根据Pontryagin最大值原理求解以上模型,列车的节能操纵策略为[14]
(1)uf(x)=1,ub(x)=0,列车全力牵引;
(2)uf(x)∈(0,1),ub(x)=0,或者uf(x)= 0,ub(x)∈(0,1),列车维持匀速;
(3)uf(x)=0,ub(x)=0,列车惰行;
(4)uf(x)=0,ub(x)=1,列车全力制动.
2 列车优化操纵策略分析
理论上,在运行距离和运行时分已经给定的前提下,列车可以有多种运行方式.列车最优运行方式是由最大加速度、巡航、惰行和最大制动这几种工况组成[15].根据许多学者的研究,节能优化操纵无非是提高惰行比例,减少制动,采用牵引惰行相结合的方式,利用现代智能算法求取最佳惰行点的位置[16].然而对于运行过程中列车采用巡航策略还是牵引和惰行相配合的能耗比较却鲜有说明.
假设列车在站间分别采用两种节能运行模式,运行模式1在S1~S2区间采用巡航方式,模式2采用牵引和惰行相结合的方式,如图1所示.
图1中,V0为巡航时恒定速度大小,两种运行模式在S1~S2区间运行时间相同,均为t0,运行距离均为s.假设列车在惰行时为减速过程,且不考虑在制动过程中的能量回收,列车在S1~S2区间运行分析如下.
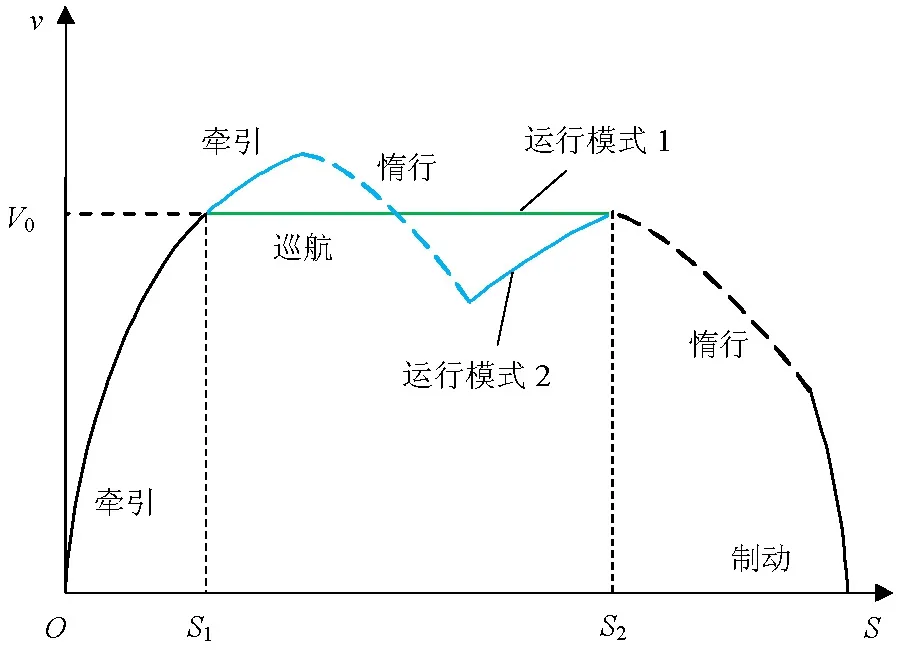
图1 列车在区间运行的两种方式Fig.1 Two patterns of train operation
根据动能定理,

式中:Wt1、Wt2为区间S1~S2中运行模式1和2对应的列车牵引力做功;相应的,Wb1、Wb2分别为制动力做功;Wr1、Wr2分别为基本阻力做功;Ww1、Ww2为线路附加阻力做功;Wh1、Wh2为势能做功.由分析可知,列车在S1和S2位置对应的动能和势能相同.整个过程中线路附加阻力和势能做功相同,故
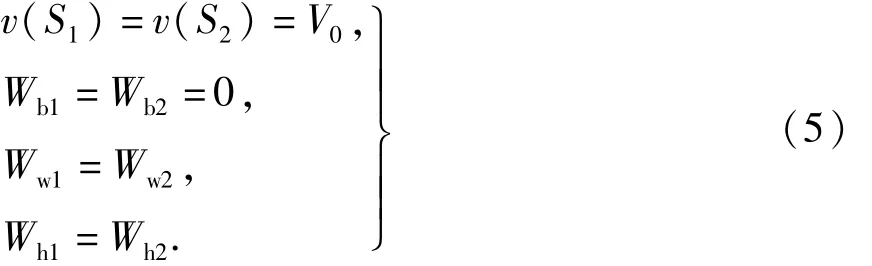
列车牵引力做功的大小即列车的牵引能耗,由式(4)可得
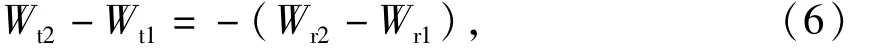
式中:Wt1、Wt2>0,Wr1、Wr2<0.
根据牛顿动力学定律,

列车运行时分满足

令
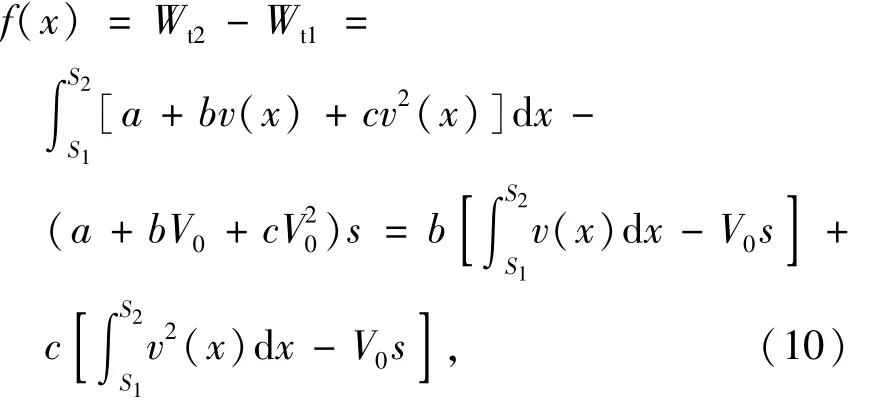
对式(10)作变形

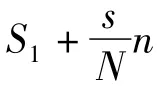
同理,对式(9)作变形

由不等式定理可知
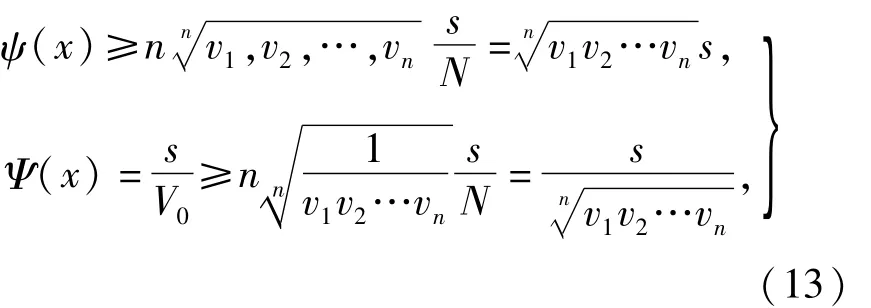
从而可得
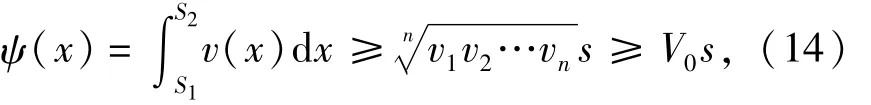
等号当且仅当v1=v2=…=vn=V0时成立.
又因为
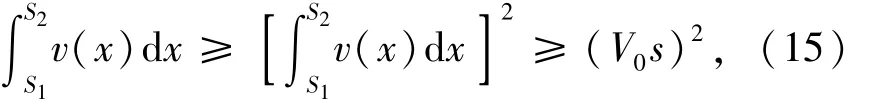
所以,可得f(x)≥0,即Wt2≥Wt1,等号当且仅当v1=v2=…=vn=V0时成立.
由以上可知,在列车初速度和末速度以及运行时分相同的情况下,列车匀速运行时基本阻力做功最小,即采用匀速运行的方式比采用牵引和惰行相结合的方式更加节能.然而,此结论需要列车在惰行时满足式(16)才能成立,

3 时间逼近搜索算法
列车运行节能操纵的一个重要原则就是尽量避免列车制动,并使列车尽可能以匀速运行.根据此结论,本文提出了一种将列车运行区间进行分段后采用时间逼近搜索优化的方法.对于具体的线路,区间分段如图2所示.

图2 列车运行区间的分段及工况优化示意Fig.2 Segmentation and optimization of train operation
图2中,每个区段对应的坡道和限速是固定的.Si为第i个区段结束的位置,Vi为第i个限速区间的限速值大小.
列车定时节能的算法过程如图3所示.
列车运行优化过程如下:
步骤1 首先,列车以最快的方式(即节时策略)运行完所有区间,得到最小运行时分tmin.
步骤2 从线路末端向起点方向搜索由高限速到低限速的过渡区段(如图2中的S5~S6区段,区段中含有制动过程),从该区段的起点开始,列车转为惰行工况.如果不存在这样的区段(例如整个线路就一个限速区间),则转到步骤5.
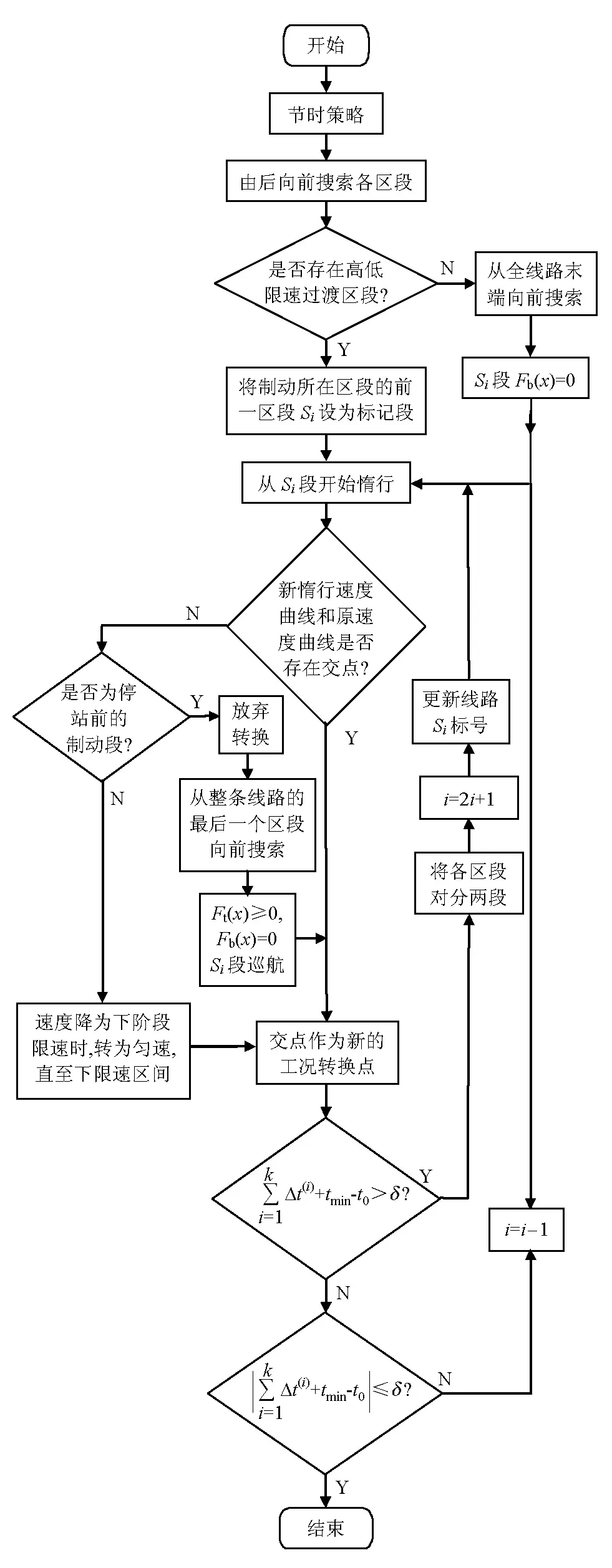
图3 定时节能计算机算法流程图Fig.3 Flow chart of energy-saving control with fixed time
步骤3 在惰行过程中,若速度上升,则列车制动以满足限速要求;若速度降低,则惰行速度曲线与原来制动速度曲线的交点作为新的工况转换点,如图2(a)中的①所示.如果没有交点,则惰行速度降至下阶段限速大小时,按匀速行驶至下个限速区间,如图2(a)中的②所示.
步骤4 每调整一次运行方式,更新列车速度曲线,列车运行时分比原先增加Δt.当满足式(18)时,取该段中间位置再次分段,并从中间新的分段位置开始退回到步骤3,该过程如图2(b)所示.当满足式(19)时,优化过程终止,否则,向线路起点方向前移一个区段,转到步骤3.

式中:k为调整工况次数;Δt(i)为第i次调整工况后增加的运行时分;t0为给定的列车运行时分;δ为能够接受的列车运行时间误差限值.
步骤5 从整条线路分段后的最后一个区段开始依次向前搜索.当搜索到Fb(x)=0时,列车工况从该段转为惰行,转到步骤3,该过程如图2(c)中的③所示.所不同的是,当惰行速度降为0,列车仍未到站时,则放弃该段工况的转换,保持原工况,并转到步骤6.
步骤6 当所有制动区段都已完成惰行的转换,列车运行总时间仍大于给定的时间t0,则从整个线路的末端开始,向起点方向搜索,依次从列车牵引加速(即满足Ft(x)≥0且Fb(x)=0)所在的区段开始,转为巡航工况,巡航速度曲线与原先的惰行曲线的交点作为新的惰行点,转到步骤4.
4 算例与测试数据比对
结合上海地铁3号线“铁力路站—友谊路站”的列车运行实测结果,对定时节能算法进行验证分析.现场测试环境如图4所示,测试时间为2014年12月12日.
两站的站间距为1.707 km,列车实际运行时间为133 s,线路坡道数据见表1,曲线信息见表2,区间限速见表3,列车起始位置在区间0.103 km处,车辆为阿尔斯通AC03车型,车辆牵引和制动特性见表4.
列车运行过程中前受电弓牵引网压、前受电弓电流及列车运行速度随时间变化关系如图5所示.
列车时间逼近搜索优化算法采用0.5 s的时间间隔进行计算,“铁力路站—友谊路站”的站间运行时分设为133 s,时间误差设定在±3%以内.优化过程中,列车运行区间分段及列车惰行起始位置如表5所示.列车运行过程中,运行时间及牵引能耗如表6所示.

图4 上海地铁3号线现场测试环境Fig.4 Field test at Shanghai Metro Line 3
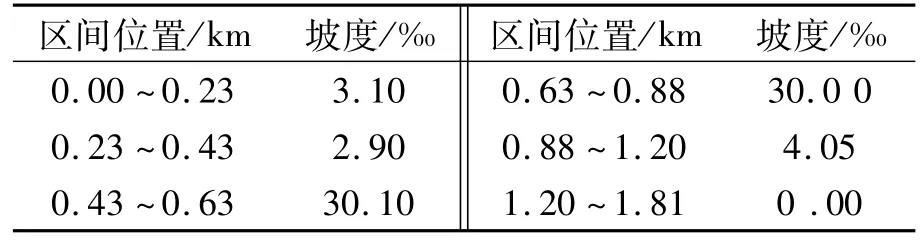
表1 铁力路站至友谊路站线路坡道信息Tab.1 Information of slopes from Tieli Road to Youyi Road

表2 铁力路站至友谊路站线路曲线信息Tab.2 Information of curves from Tieli Road to Youyi Road

表3 铁力路站至友谊路站线路限速信息Tab.3 Speed limits from Tieli Road to Youyi Road
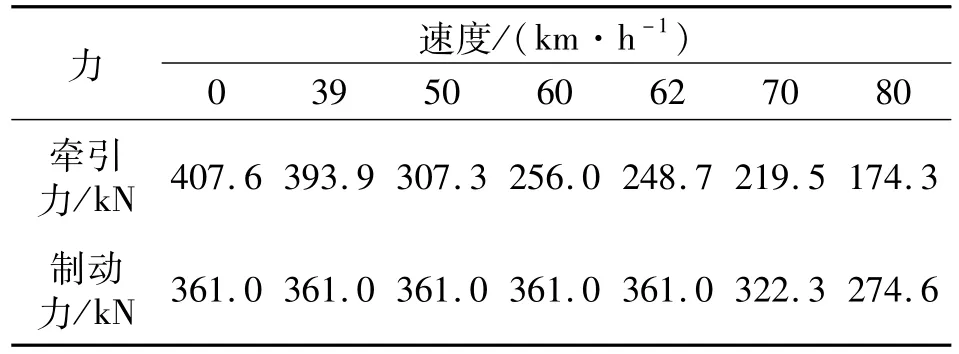
表4 车辆牵引和制动特性Tab.4 Train traction and braking characteristics
由仿真结果可知,随着列车惰行距离的增大,列车运行时间增加,相应的牵引能耗减小.根据实测结果,列车在“铁力路站—友谊路站”之间的牵引能耗为53.85 kW·h,运行时间为133 s.列车在第三次搜索优化后,运行时间超过正偏差上限值,所以对区间分段进行调整.而经过第4次搜索优化之后,列车运行时间误差满足设定要求,且列车运行能耗为47.10 kW·h,节能12.5%.算法寻优过程以及实测速度曲线对比如图6所示.列车实际运行过程中采用牵引和惰行相结合的策略,而本文中的优化算法是使列车在避免不必要制动的基础上,尽可能保持匀速运行,从而达到定时节能运行的目的.
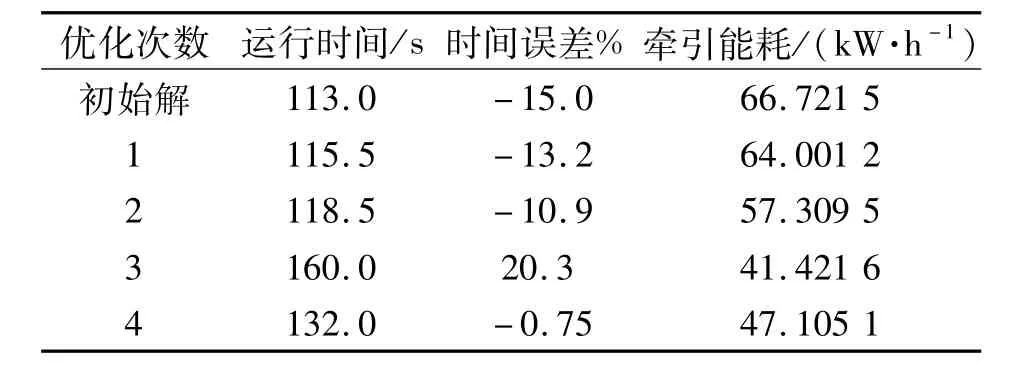
表6 时间逼近搜索优化算法仿真结果Tab.6 Simulation results of time-approaching search method
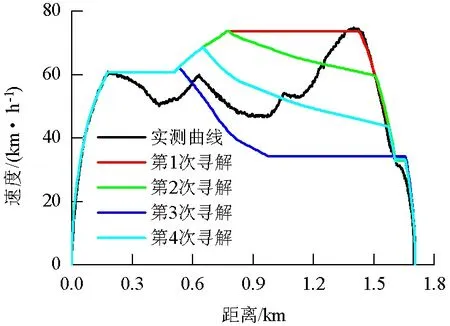
图6 算法寻优过程以及实测速度曲线对比Fig.6 Algorithm optimization process compared with the measured speed curve
5 结 论
本文对城市轨道交通列车节能优化算法进行了深入的研究,推导了列车定时节能优化模型,从数学解析的角度分析了列车在特定条件下的最佳节能操纵策略.设计了一种将列车运行区间分段后采用时间逼近搜索的节能优化方法,并开发了相应的牵引计算软件.上海地铁3号线“铁力路站—友谊路站”的仿真结果表明:使用时间逼近搜索优化算法后,列车运行时分误差为-0.75%,牵引能耗相比实际能耗降低12.5%,同时算法具有较快的计算速度.然而算法在求解过程中,如果惰行位置恰好发生在长陡下坡,且列车需要使用制动工况维持速度在限速值以下,则会增加时间逼近搜索次数,影响求解效率,在以后的研究中需要加以改进.
[1] 唐海川,王青元,冯晓云.地铁列车追踪运行的节能控制与分析[J].铁道学报,2015,37(1):37-43.
TANG Haichuan,WANG Qingyuan,FENG Xiaoyun. Energy saving control of metro train tracing operation[J].Journal of the China Railway Society, 2015,37(1):37-43.
[2] LIU R R,GOLOVITCHER IM.Energy-efficient operation of rail vehicles[J].Transportation Research Part A:Policy and Practice,2003,37(10):917-932.
[3] LU S,HILLMANSEN S,HO T K,et al.Single-train trajectory optimization[J]. IntelligentTransportation Systems,IEEE Transactions on,2013,14(2):743-750.
[4] KO H,KOSEKI T,MIYATAKE M.Application of dynamic programming to optimization of running profile of a train[J].Computers in Railways IX,2004(15):103-112.
[5] BOCHARNIKOV Y V,TOBIAS A M,ROBERTS C,et al.Optimal driving strategy for traction energy saving on DC suburban railways[J].Electric Power Applications,IETE,2007,1(5):675-682.
[6] CHUANG H J,CHEN C S,LIN C H,et al.Design of optimal coasting speed for saving social cost in mass rapid transit systems[C]∥Proceedings of the Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies.Piscataway:IEEE Press,2008:2833-2839.
[7] ACIKBAS S, SYLEMEZ M T. Coasting point optimization for mass rail transit lines using artificial neural networks and genetic algorithms[J].Electric Power Applications,IET,2008,2(3):172-182.
[8] CHEVRIER R,MARLIEERE G,VULTURESCU B,et al.Multi-objective evolutionary algorithm for speed tuning optimization with energy saving in railway:application and case study[J/OL].(2011-01-01)[2015-05-22]. https://www. researchgate. net/ publication/50365605.
[9] 杨利军,胡用生,孙丽霞.城市轨道交通节能线路仿真算法[J].同济大学学报:自然科学版,2012,40(2):235-240.
YANG Lijun,HU Yongsheng,SUN Lixia.Energysaving track profile of urban mass transit[J].Journal of Tongji University:Natural Science,2012,40(2):235-240.
[10] WANG Penling,LIN Xuan,LI Yuezong.Optimization analysis on the energy saving control for trains with adaptive genetic algorithm[C]∥ Systems and Informatics(ICSAI),2012 International Conference on.Yantai:IEEE,2012:439-443.
[11] 王鹏玲,林轩,李跃宗,等.自适应遗传算法在列车节能优化中的应用[J].计算机仿真,2012,29(11):350-354.
WANG Pengling,LIN Xuan,LI Yuezong,et al. Energy saving train operation optimization with adaptive genetic algorithm[J].Computer Simulation,2012,29(11):350-354.
[12] 刘炜,李群湛,郭蕾,等.基于多种群遗传算法的城轨列车节能运行优化研究[J].系统仿真学报,2010,22(4):921-925.
LIU Wei,LI Qunzhan,GUO Lei,et al.Study of urban railway energy saving train control optimization based on multi-population genetic algorithm[J]. Journal of System Simulation,2010,22(4):921-925.
[13] 饶忠.列车牵引计算[M].北京:中国铁道出版社,2006:48-53.
[14] GU Qing,TANG Tao,GAO Fang,et al.Energyefficient train operation in urban rail transit using realtime traffic information[J].Intelligent Transportation Systems,IEEE Transactions on,2014,15(3):1216-1233.
[15] 王青元,冯晓云.考虑再生制动能量利用的高速列车节能最优控制仿真研究[J].中国铁道科学,2015,36(1):96-103.
WANG Qingyuan,FENG Xiaoyun.Simulation study on optimal energy-efficient control of high speed train considering regenerative brake energy[J]. China Railway Science,2015,36(1):96-103.
[16] 韩蕙心,吴鹏,吴杰,等.基于多目标差分进化算法的列车惰行控制[J].计算机应用,2013,33(增刊2):286-289.
HAN Huixin,WU Peng,WU Jie,et al.Coast control of urban train based on multi-objective differential evolution algorithm[J]. Journal of Computer Applications,2013,33(Sup.2):286-289.
基于时间逼近搜索算法的城轨列车运行节能优化研究
刘 炜, 王 栋, 李群湛, 崔梦雨
A Novel Time-Approaching Search Algorithm for Energy-Saving Optimization of Urban Rail Train
LIU Wei, WANG Dong, LI Qunzhan, CUI Mengyu
(School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
To ensure energy-saving and punctual operation of urban railway,a time-approaching search method was proposed.The energy-saving control model of urban railway that satisfies timing running was established.A set of optimal conditions for energy-saving control was derived according to the Pontryagin maximum principle.The energy consumption of a train under different energy-saving operations was calculated.On this basis,we presented an optimization method of dividing the train operation period into sections.The change point of train operation is determined using timeapproaching search method to meet the requirements of energy-saving and timing.A section from Tieli Road to Youyi Road of Shanghai Metro Line 3 is taken as an example.Compared with measurement results in the practical loading process,the energy comsuption is reduced by 12.5% using timeapproaching search algorithm.
Urban rail transit;energy saving control;time-approach;optimization
刘炜,王栋,李群湛,等.基于时间逼近搜索算法的城轨列车运行节能优化研究[J].西南交通大学学报,2016,51(5):918-924.
0258-2724(2016)05-0918-07
10.3969/j.issn.0258-2724.2016.05.014
U292
A
2015-06-24
国家自然科学基金资助项目(51607148);中国铁路总公司科技研究开发计划资助项目(2014J009-B)
刘炜(1982—),男,副教授,博士,研究方向为列车运行优化、牵引供电系统仿真,E-mail:liuwei_8208@swjtu.cn
(中文编辑:唐 晴 英文编辑:周 尧)

