有砟轨道动刚度特性研究

亓　伟，陈伯靖，段海滨，刘玉涛

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都　610031；2.四川水利职业技术学院，四川崇州　611830)



有砟轨道动刚度特性研究

亓伟1，陈伯靖2，段海滨1，刘玉涛1

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都610031；2.四川水利职业技术学院，四川崇州611830)

为充分了解轨道动力特性，对有砟轨道动刚度展开研究。通过建立有砟轨道力学模型，分析0～2 000 Hz范围内轨道动刚度的振动特性，得出：轨道动刚度相对于轨道静刚度是随激振频率变化的，轨道动刚度在低频段受激振频率变化影响较小，在中、高频段内轨道动刚度振动幅值随激振频率变化而变化，是系统的固有特性，需通过对构件刚度、阻尼等参数调节。阻尼系数对轨道动刚度的幅值有影响，但不改变轨道的共振频率。质量阻尼系数对轨道动刚度波动范围及幅值的影响小于刚度阻尼系数的影响。阻尼系数增大，轨道动刚度波动幅值增大。

有砟轨道；动刚度；振动特性；阻尼系数

动刚度是引起钢轨竖向单位动位移所需要的力，反映刚度与振动频率之间的关系，是轨道动态性能评价的重要指标之一。随着高速铁路的迅速发展，对轨道平顺性提出了很高的要求，仅考虑轨道静态几何形位的平顺性已难以满足要求，还需要深入研究轨道动平顺性，即轨道动刚度的倒数动柔度的平顺性。

1　轨道动刚度

轨道动刚度是随激振频率发生变化的，而静刚度是系统在静力作用下的变形，静刚度可看成是动荷载在激振频率为0时动刚度的特殊形式。轨道承受来自列车动荷载的激振频率范围较大，动刚度变化较大，因此需对轨道动刚度展开研究。

在系统动刚度的研究中，一般将系统看作线性系统，激励输入到线性系统内，输出对应的响应，如图1所示。系统的这种传递特性可通过传递函数表达，传递函数在不同的学科有不同的名称，在力激励与位移响应中称为位移导纳或动柔度，而动刚度是动柔度的倒数。传递函数与激振频率和系统参数(刚度、阻尼、质量等)有关。对于轨道动刚度的计算，具体参考文献[1]。

图1系统、激励和响应的关系示意

机械学科对系统动刚度研究较多，且多注重机械振动中减振降噪、提高设备稳定性等方面的研究。为提高机床精度、稳定性、延长设备寿命，需从系统动刚度出发，通过改变系统主振频率方面实现，如文献[2-3] 为保证机械设备在振动过程中的安全性和精确度，基于模态柔度、弹性能量分布理论等确定出机床结构的薄弱模态和薄弱结合部，进而确定优化方向，通过分析各结合部的动刚度对机床动态性能的影响程度，得到结合部动刚度的最优配置方案。动刚度特性是衡量系统结构稳定性和抗振能力的重要指标，航空航天飞行器等方面为保证器械的稳定性/安全性，在系统动刚度、部件动刚度方面都做了深入研究，文献[4-5] 为保证航空发动机能够安全稳定地工作，避免航空发动机在工作的过程中出现较大的振动，根据发动机实际结构建立发动机后支承动力学模型，通过锤击试验法与有限元分析法得到发动机后支承的动刚度曲线，验证了有限元分析的正确性，为进一步研究发动机稳定性提供了理论依据。

随着对结构振动研究的深入，土木行业逐渐加深对系统动刚度的研究。文献[6]采用落轴试验测试了不同道床材质、厚度、密实度以及脏污情况下的有砟道床动刚度和阻尼值，文中对有砟道床时程曲线内的数据进行了分析，但未进行频域分析。在频域分析方面，对轨道动刚度研究主要集中在轨道构件的减振效果研究。文献[7-10]分析了轨道减震器、弹性支承块、浮置板等在中频振动荷载作用下的振动特性，通过对传递力、功率流、动刚度、损耗因子等因素进行评价，得出较为合理的降低中频轮轨动态力的方案。

轨道的动刚度研究不能仅仅局限于扣件、弹性支承块或浮置板等某一层的振动，亦不能仅按照轨道各层结构建立几个简单自由度的力学模型代替，因为轨道的动刚度是由扣件、轨枕、轨下基础等组成的一个多自由度复杂系统。根据国内外专家学者已做的工作，根据路基上有砟轨道的结构形式简化建立了相应的力学模型，研究了轨道动刚度与激励频率变化的关系，同时分析了系统阻尼对轨道动刚度的影响。

2　力学模型

根据有砟轨道各构件参数建立相应的力学模型，如图2所示。轨道垂向动刚度主要与列车垂向荷载有关，故模型中仅考虑轨道结构在垂向稳态激励作用下的响应。模型中将钢轨、轨枕简化为梁；有砟道床为散体道砟组成的，模型中将道床简化为道床质点与道床竖向弹簧；扣件、路基简化为竖向弹簧；为消除边界效应，取轨道长度为50根轨枕长度。为分析不同频率荷载作用下有砟轨道的响应，对模型中钢轨中点作用F=F0eiωt的荷载，其中，F0为列车静轴重，ω为激振频率。对于模型的谐响应分析采用模态叠加法，高速列车轴重集中在140～170 kN，选取轴重150 kN进行分析。参考文献[11]，选取扣件刚度60 kN/mm，道床刚度(半根轨枕下支承刚度)200 kN/mm，路基刚度(半根轨枕下支承刚度)160 kN/mm进行计算。轨枕采用Ⅲ型轨枕，钢轨为60 kg/m钢轨，具体参数见文献[11]。列车-轨道系统是一个复杂的多自由度系统，各个构件有各自的主振频率，本文研究的频率范围为包含高中低频范围的0～2 000 Hz。

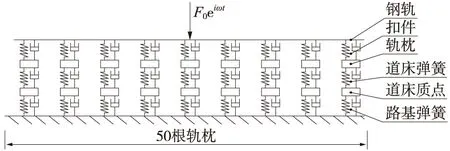
图2　有砟轨道力学模型

模型中阻尼采用瑞利阻尼法计算，[C]=α[M]+β[K]，具体取值见式(1)～式(3)

(1)

(2)

(3)

式中，ξ为黏性比例阻尼系数，为讨论阻尼的影响，文中黏性比例阻尼系数ξ根据常规取值为0.03～0.05；f1为低频荷载；f2为高频荷载。本文计算取低频0 Hz，高频2 000 Hz，所以β1=4.77×10-6，β2=6.36×10-6，β3=7.95×10-6，由于当低频为0 Hz时的质量阻尼系数为0，为研究质量阻尼的影响，本文选取α1=0，α2=0.5，α3=1。对于轨道动刚度的研究，阻尼系数选取α1、β1，其他参数分别用于研究质量系数与阻尼系数对于轨道动刚度的影响。

3　激励频率对轨道动刚度的影响

轨道静刚度为动刚度激振频率为0时的特殊动刚度，由计算结果知，当阻尼系数取α1、β1时的轨道静刚度为37.908 kN/mm，与该模型静力分析中轨道静刚度37.911 kN/mm的误差小于万分之一。

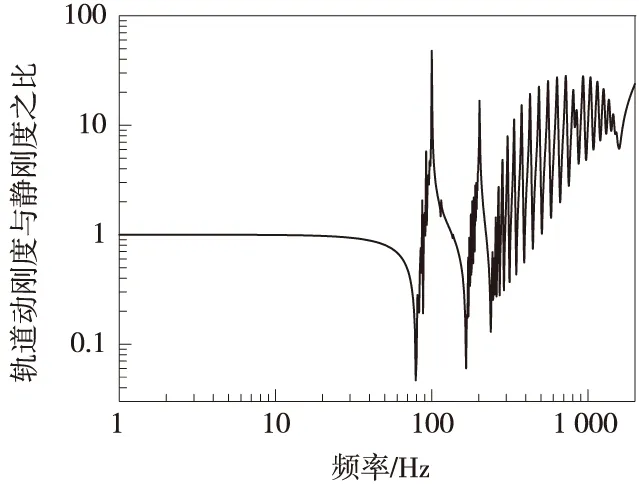
图3　有砟轨道动刚度与静刚度的比值

将不同激振频率下的轨道动刚度与静刚度作比较，如图3所示：在低频段，随着激振频率的增加，轨道动刚度略有减小。当激振频率达到79 Hz时，达到轨道系统的第一主振频率，轨道此时振动幅度最大，动刚度达到最小值1.77 kN/mm，仅为静刚度的4.68%。随后轨道动刚度随着激振频率的增大迅速增大，当激振频率为100 Hz时，轨道动刚度达到最大值183.12 kN/mm，为静刚度的47.8倍。之后轨道动刚度随着激振频率的增加波动增加。

文献[12-13]指出：0～20 Hz范围内的低频振动对人体危害最大，0～2 Hz是列车车体主振频率，0 ～50 Hz的低频段是轨枕、道床等轨下基础与列车构架的主振频率，轮轴系统主振频率在400～600 Hz的中频段，轮轨振动及噪声主要与高频振动有关，通常根据钢轨pined-pined频率划分轨道的中、高频段，故将1 600 Hz以上的频率作为高频区段进行分析。对比有砟轨道动刚度计算结果可知，因为低频段(0～50 Hz给出范围)轨道动刚度变化很小(图4)，所以轨道在低频段振动很小，从而保证了乘车舒适性，同时减小了列车车体与轨道结构的疲劳伤损。轨道在中频段(400～600 Hz)的动刚度如图5所示，在中频段，动刚度的振幅随着激振频率的增加波动增大，轨道动刚度的波动与轨道各构件固有频率有关，对应的动刚度是各阶模态结果叠加的结果，因为各阶模态对应的曲线有相应的波动曲线，各曲线叠加之后出现中频段的动刚度周期性波动，这些波动是系统的固有特性，只可通过相应措施减小波动但不能消除振动。高频段(1 600 Hz以上)轨道动刚度(图6)在1 600 Hz之后轨道动刚度随着激振频率的增加而增大，由此可知，轨道动刚度在高频段对轨道振动的影响较小，可重点研究轨道的中、低频段动刚度。

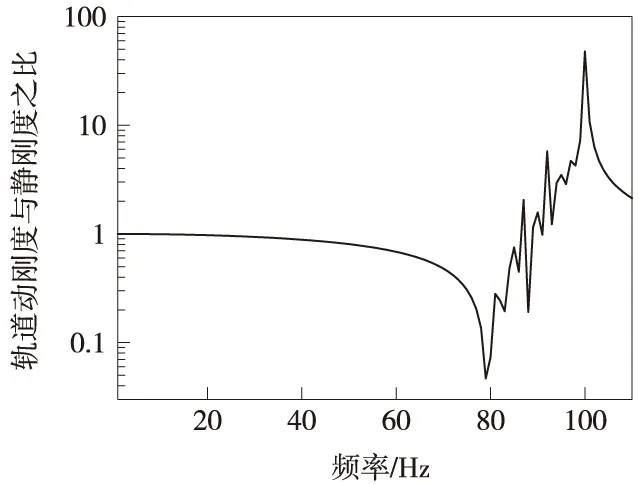
图4　有砟轨道动刚度与静刚度的比值(低频段)

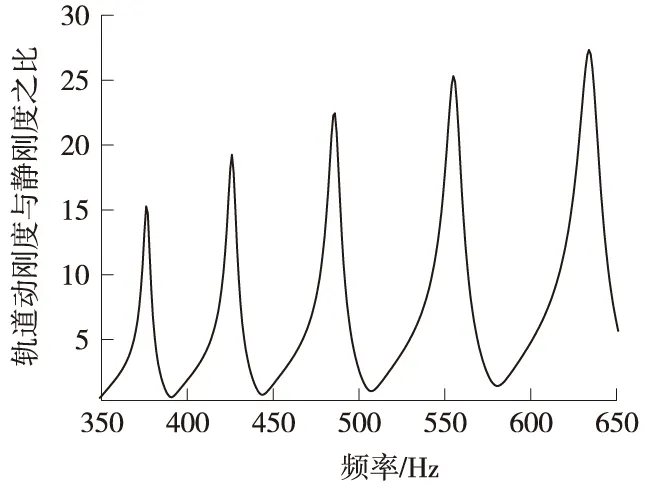
图5　有砟轨道动刚度与静刚度的比值(中频段)

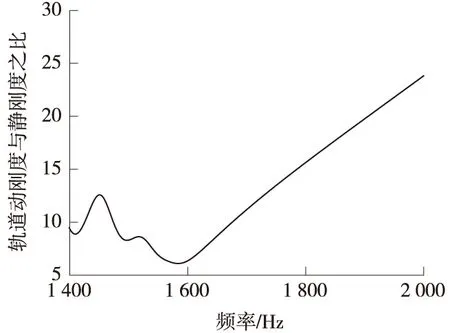
图6　有砟轨道动刚度与静刚度的比值(高频段)

4　系统阻尼的影响

阻尼是影响轨道动刚度的一个重要影响因素，图7为质量阻尼系数分别为α2、α3时的轨道动刚度与质量阻尼系数为α1时的轨道动刚度之比。

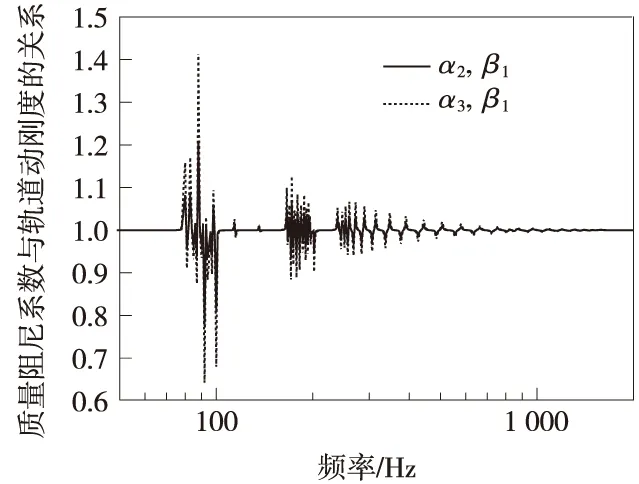
图7　质量阻尼对轨道动刚度的影响

由图7可知，质量阻尼主要影响频率在100 Hz与200 Hz频段附近的轨道动刚度。当质量阻尼为α2时轨道动刚度与α1时的轨道动刚度比值波动范围在0.78～1.20倍之间，当质量阻尼为α3时轨道动刚度与质量阻尼为α1时的轨道动刚度比值波动范围在0.64～1.41倍之间，由此可知，随着质量阻尼系数的增大，轨道动刚度的幅值变化相应增大。图8为刚度阻尼系数分别为β2、β3时的轨道动刚度与刚度阻尼系数为β1时的轨道动刚度之比。

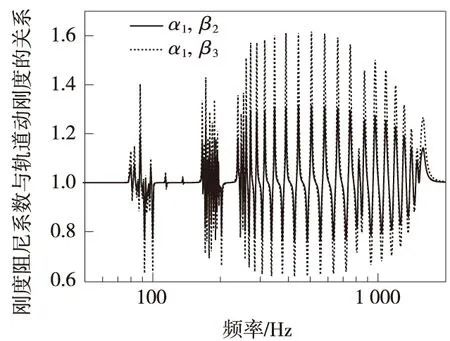
图8　刚度阻尼对轨道动刚度的影响

由图8可知，刚度阻尼对轨道动刚度的影响范围较广，涵盖激励荷载的低、中、高频段。当质量阻尼为β2时轨道动刚度与β1时的轨道动刚度比值波动范围在0.76～1.32倍之间，当刚度阻尼为β3时轨道动刚度与刚度阻尼为β1时的轨道动刚度比值波动范围在0.63～1.62倍之间，由此可知，随着刚度阻尼系数的增大，轨道动刚度的幅值变化相应增大。

轨道的系统阻尼变化对轨道的共振频率无影响，但是对轨道动刚度的振动幅值影响较大，合理的设置轨道系统质量阻尼系数与刚度阻尼系数能够实现减振降噪，减小轨道结构、列车构件伤损的目的。

5　结论

轨道动刚度是研究高速列车安全平稳运行的重要参数，不同于轨道静刚度有一个确定的值，轨道动刚度是随荷载激振频率变化的。本文通过建立有砟轨道力学模型，分析了在0～2 000Hz范围内轨道动刚度与荷载激振频率的变化规律，主要结论如下。

(1)轨道动刚度不同于静刚度的一成不变，随激振频率的变化而变化，当质量阻尼系数为α1、刚度阻尼系数为β1时的波动范围介于静刚度的0.046 8～47.6倍之间。

(2)轨道动刚度在低频段受激振频率变化影响较小，保证了乘车舒适性，同时减小了列车车体与轨道结构的疲劳伤损；在中、高频段内轨道动刚度振动幅值波动较大，是系统的固有特性，需通过调节构件刚度、阻尼等参数来改善。

(3)阻尼系数对轨道动刚度的幅值有影响，但不改变轨道的共振频率。质量阻尼系数对轨道动刚度波动范围及幅值的影响小于刚度阻尼系数的影响。阻尼系数增大，轨道动刚度波动幅值增大。

[1]李成辉.振动理论与分析基础[M].成都：西南交通大学出版社，2015.

[2]周生通，李鸿光，等. 重型动平衡机摆架的动刚度测试与动力特性预计[J].机械工程学报，2014，50(8):1-9.

[3]邓聪颖，殷国富.基于正交试验的机床结合部动刚度优化配置[J].机械工程学报，2015，51(19):146-153.

[4]李玲玲，王克明.某型航空发动机后支承动刚度的有限元计算[J].沈阳航空工业学院学报，2007，24(3):5-7.

[5]赵文涛，陈果.航空发动机机匣支承动刚度有限元计算及验证[J].航空计算技术，2011，41(5):34-41.

[6]刘卫星，王午生.铁路碎石道床动刚度与阻尼的试验研究[J].铁道学报，2002，24(6):99-104.

[7]张波，张涛.城市轨道交通工程聚氨酯浮置板减振道床技术应用研究[J].铁道标准设计，2014，58(7):45-48.

[8]荆果，代齐齐.轨枕间距对钢轨振动的影响研究[J].铁道标准设计，2011(10):30-32.

[9]S.L.Grassie.TheDynamicResponseofRailwayTracktoHighFrequencyVerticalExcitation[J].JournalofMechanicalEngineeringScience， 1982，24(2):77-89.

[10]吴天行.轨道减振器与弹性支承块或浮置板轨道组合的隔振性能分析[J].振动工程学报，2007，20(5):489-493.

[11]翟婉明.车辆-轨道耦合动力学[M].4版.北京：科学出版社，2015:517-520.

[12]刘林芽，刘海龙，雷晓燕.轮轨系统车轮的高频振动特性[J].交通运输工程学报，2011(6):44-49.

[13]任尊松，刘志明.高速动车组振动传递及频率分布规律研究[J].机械工程学报，2013，49(16):1-7.

Study on Dynamic Stiffness of Ballasted Track

QI Wei1， CHEN Bo-jing2， DUAN Hai-bin1， LIU Yu-tao1

(1.MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China;2.Sichuan Water Conservancy Vocational College， Chongzhou 611830， China)

In order to understand the dynamic characteristics of rail track， a mechanical model of ballast railway track is developed to analyze the dynamic stiffness under excitation frequency ranging from 0Hz to 2000Hz. The dynamic stiffness varies with excitation frequency， which is different from the static stiffness. The excitation frequency has little effect on dynamic stiffness in case of low frequency， but the amplitude varies with the excitation frequency in mid and high frequencies. As it is an inherent characteristic， such measures as adjusting the stiffness or damping of components can be taken to diminish the effect. The damping coefficient of the railway track has some effect on the amplitude of dynamic stiffness but has no effect on resonant frequency. Mass damping coefficient has a smaller effect on the scope and amplitude of dynamic stiffness than stiffness damping coefficient. The amplitude of dynamic stiffness increases with the increasing of damping coefficient．

Ballast railway track; Dynamic stiffness; Characteristics of vibration; Damping coefficient

2016-01-27；

2016-03-02

国家杰出青年科学基金(51425804)；国家自然科学基金(重点项目)(U1334203&U1234201)

亓伟(1989—)，男，博士研究生，E-mail：qw9199@126.com。

1004-2954(2016)09-0032-04

U211.3

ADOI:10.13238/j.issn.1004-2954.2016.09.007