陀螺进动机理研究及稳定性分析

邓景元

（中国人民大学附属中学，北京 100080）

陀螺进动机理研究及稳定性分析

邓景元

（中国人民大学附属中学，北京 100080）

陀螺力学在现代工程技术与天文物理研究中应用广泛。陀螺仪由于具有良好的高速自旋稳定性，在飞机和船舶的惯性导航与控制、隧道和石油勘探的精密定位仪器等诸多领域被广泛采用。本文通过角动量定理简明直观的推导论述了陀螺的进动过程，并探讨了其在外界微小扰动下的稳定性，指出了高速自旋的陀螺具有良好的抵御外界扰动的能力及其物理力学背景。

陀螺力学；进动与章动机理；进动稳定性； 角动量定理

0　引言

高速旋转的陀螺在受到外界微小扰动时，并不会倒下而是陀螺自身的对称轴将绕空间中的固定轴做微小的摆动。陀螺这种良好的抵御外力而保持稳定的能力，使得其广泛的应用于现代工程技术中，如飞机和船舶的惯性导航与控制、隧道和石油勘探的精密定位仪器，以及微机电系统中的各种惯性传感器［1］等。陀螺的运动可以用传统的刚体动力学进行描述。陀螺的运动具有良好的定轴性，在受到外力矩的作用下会发生进动和章动。这种运动模式在天体物理中也频繁出现，行星或卫星在只受到中心引力的作用下，其轨道法向在惯性空间保持不变，而在受到微小外力后，轨道面会发生进动。以地球为例［2］，地球自转的瞬时轴为地轴，地轴在旋进运动时与黄道面法线的夹角也会微小变化，这成为地球的章动，而天文学中观察到的岁差与章动来自同样的原因：（1）地球形状本身的扁平型和地轴的倾斜性；（2）月球或太阳对地球引力的不均匀性。因此，对陀螺进动和章动的动力学分析，无论是对于现代工程技术，还是天文物理科学的发展都具有重要的意义。陀螺仪基于严格数学处理的动力学分析较为复杂，对工程实际的应用具有一定的难度。本文从刚体动力学出发，简明扼要的推导了陀螺的进动机 理；从微小扰动的角度出发进一步给出了进动稳定性和章动的简化解析式，详细的探讨了陀螺仪在受到微小扰动后的动力学过程和稳定性条件。

1　陀螺进动过程分析

如图1（a）所示，陀螺底端与地面接触点为O点，在固定坐标系OXYZ中的陀螺绕其自身的旋转轴OZ'处于高速自旋状态，旋转角速度为ω，自身旋转轴OZ'和固定坐标系OZ轴的夹角为θ，质量为m的陀螺重心为图中C点。为简化问题描述，设此时陀螺刚好运动至YOZ平面（即OZ'轴运动 至在YOZ平面内），陀螺绕OZ'轴的转动惯量为J。

经过初步分析，可以得到当陀螺自旋角速度极低或者不转动时，陀螺将无法保持稳定而倒下。当陀螺以一定角速度ω自转时，在重力绕OZ轴的力矩作用下，陀螺自转轴OZ'还将会绕着OZ轴“公转”，这种“公转”运动就是陀螺的进动。陀螺运动过程受到的诸多力之中只有重力存在绕着OZ轴的力矩，该力矩的方向在所研究时刻（即OZ'轴运动至在YOZ平面内时）垂直于YOZ平面，重心C到O点的距离为l，在Δt时间内，自转轴OZ'绕OZ轴转过的角度为Δα，如图 1（b）所示。由角动量定理可得：

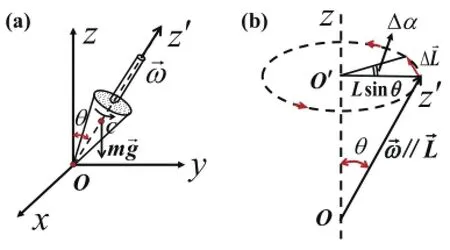
图1　（a） 陀螺自旋模型图　　 （b） 陀螺进动力学分析图

由上式可得，陀螺进动角速度为：

由上式即可得到进动角速度Ω与重力矩和角动量相关。随着陀螺自转角速度增大，进动角度会减小。需要说明的是，转动惯量J与陀螺自身质量存在较大的关联，因此上式主要说明了陀螺进动角速度与自转角速度的关系。特别地，当自转角速度特别小，即ω→0时，可以得到Ω→+∞，这与实际情况相违背，因此此时陀螺已经无法稳定；实际上，当ω特别小的时候，陀螺由于自身的惯性效应，无法提供一个大的进动角速度而维持稳定状态，因此，一般来讲，所研究的陀螺运动都是考虑自转角速度远大于进动角速度。同时，考虑到自转角速度的矢量性，在同等大小的自转角速度下，方向相反后，也会导致进动角速度反向。

因此，在各式各样的微精密仪器中，可以通过调整陀螺仪自身的自转角速度方向从而实现对进动角速度方向的调节与控制。

2　陀螺进动稳定性分析

如第 节所述，在陀螺进动过程中存在微小扰动时，会出现自转轴上下的小摆动，这种小的摆动就是章动。对章动的研究一方面可以更加深入的认识陀螺进动的稳定性；另一方面可以对各种天文现象进行更加合理的解释。在不考虑外界微小扰动时，陀螺的自转轴OZ'端部能绕OZ轴作圆周运动。在获得了一些初始的扰动后，端部就会在ZOZ'平面上绕先前的圆周运动轨迹有上下的摆动，如图2所示。英国天文物理学家布拉德雷（J.Braley）观测得到地球地轴的章动周期大约为18.6年，而在我国古代历法中就把19年成为一“章”，这就是最初对陀螺 力学中“章动”的认识和论述。

图2　（a）陀螺章动示意图　 （b）陀螺章动动力学分析

如图 2所示，在一个很短的Δt1时间内，陀螺受到一个力矩M1的作用，使得其自转轴OZ' 在ZOZ'面内由图示中的OZ1'的位置偏移至OZ2'的位置，在此过程中，角动量的变化为LΔθ。由角动量定理可以得到有：

可得有由于外力矩M1的作用，偏转角Δθ为：

由上式可知，一方面对于高速自旋的陀螺，小扰动导致的偏转角度Δθ会非常小，其对称轴方向几乎不变。因此，高速自旋的陀螺具有短时间抗干扰的能力，而且自转角速度越大，这种抗干扰的能力越强。利用陀螺这种自旋稳定性，可以将高速自旋的陀螺仪安装在飞行器、舰船等载体上，并让其自转轴指向固定的方位，则当载体姿态发生变化时，能用陀螺装置系统进行测量和控制。

另一方面，当陀螺受到较长时间的干扰，即公式（4）中的外力矩冲量M1Δt1较大时，陀螺会发生显著的偏移，这种偏移导致的结果是使得在垂直于ZOZ'平面存在一个新的角动量分量，使得第2节中的公式（1）对应的角动量定理右侧有新的角动量项，最终使得陀螺在ZOZ'平面内存在周期性摆动的章动模式。进一步地，章动过程中，综合考虑外力矩M的作用，取Δt时间进行研究，根据角动量定理，陀螺下倾的角动量为［3］：

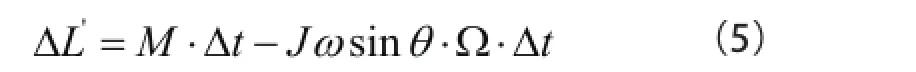
其中，上式等号右侧第二项为稳定旋进状态对应的角动量增量。最初ΔL'＞0，即外力矩相对较大、破坏稳定进动状态时，可得，此时陀螺将继续偏离初始稳定进动的位置，使得图2（b）中的θ角继续增大。随着θ的继续增大使得ΔL'=0即时，陀螺角动量不再增加，但是θ角会由于惯性继续增长，从而导致ΔL'＜0即Ω，陀螺由此得到了回复到初始位置的角动量，自旋轴对应的θ角由增大变为减小，从而使得发生θ角的周期性摆动，即章动。

3　总结

陀螺力学在现代工程技术与天文物理科学的研究中都具有重要的意义。在飞机和船舶的惯性导航与控制、隧道和石油勘探的精密定位仪器，以及微机电系统中的各种惯性传感器等各种尖端科技与工程领域应用广泛。

本文系统性的对陀螺进动过程进行了论述，通过角动量定理推导了陀螺进动角速度与自旋速度的关系，并详细探讨了在外界微小扰动作用下的进动稳定性。

［1］ 成宇翔. MEMS微陀螺仪研究进展［J］.微纳电子技术，2011.5，48（5）：277～285.

［2］ 于凤军.地球章动原因的分析与计算［J］.大学物理，2011.9，30（9）：1～9.

［3］ 廖耀发，等.陀螺与陀螺仪进动及章动的一种初等分析［J］. 2004.10， 19（5）：43～46

TH21

A

1671-0711（2016）08（下）-0062-02