基于关键质量特性的农机零部件可靠性优化设计

周晨，林卫国，郑相周，徐红梅

（华中农业大学工学院，湖北 武汉 430070）

基于关键质量特性的农机零部件可靠性优化设计

周晨，林卫国*，郑相周，徐红梅

（华中农业大学工学院，湖北 武汉 430070）

质量是现代农机装备市场竞争力的一个重要因素。本文将顾客需求的模糊概念量化并融入农机零部件可靠性设计之中，提出了一种基于关键质量特性的可靠性优化方法。首先，运用模糊回归理论优化质量功能配置和公理设计的集成模型，提取农机产品设计各阶段的关键质量特性；其次，以可靠性设计理论和应力—强度干涉模型为指导，建立基于关键质量特性的农机零部件可靠性优化设计数学模型；最后，运用带约束的自适应粒子群算法对该数学模型进行求解分析。以水稻摆栽机为例，详细分析了提取零部件关键质量特性即拨盘轴设计参数流程，并分别计算了可靠度在0.995和0.999时的优化设计参数，通过Monte-Carlo法对比，其拨盘轴最优截面积相对误差分别为2.53%和2.40%。实验验证了关键质量特性分析在农机零部件可靠性优化设计中的正确性和高效性。

关键质量特性；质量功能配置；模糊回归；可靠性；粒子群算法

周晨， 林卫国， 郑相周， 徐红梅. 基于关键质量特性的农机零部件可靠性优化设计［J］. 农业现代化研究， 2016， 37（2）： 402-408.

Zhou C， Lin W G， Zheng X Z， Xu H M. Reliability-based optimization and design of the agricultural machinery parts based on key quality characteristics［J］.

Research of Agricultural Modernization， 2016， 37（2）： 402-408.

质量对农机产品的市场竞争起到核心作用。研究表明，产品设计阶段的花费仅占总成本的5%左右却决定了产品质量和成本的70%-80%［1］。根据全国各级农机质量投诉监督机构调查报告，目前农机产品突出问题是大量故障集中于零部件、易损件的可靠性较差［2］。由此可见，将可靠性优化设计应用于农机产品改进设计中，对提升农机产品质量及改善客户体验意义重大。

通常针对机械产品结构可靠性设计，往往是从载荷的性质、材料参数、几何尺寸和边界条件等去进行建模分析，设计上依赖于力学、运动学和动力学分析［3］。Charnes和Coope提出了随机规划方法，而后被众多学者广泛应用于结构安全设计中［4］；陈立周［5］提出一种基于概率密度函数矩不等式的契比雪夫点法，在保证了概率计算精度的同时，克服了广义模拟优化方法计算量大的缺点；王倩倩等［6］在一般随机有限元基础上，结合四阶矩技术、最大熵理论及不完全概率信息分析方法，在随机参数联合概率密度函数未知条件下，运用非线性动态随机结构系统分析方法解决了齿轮耦合振动的可靠性问题；Youn和Choi［7］对几种处理概率约束的方法，从精度、稳定性和效率等方面进行分析比较，为可靠性优化设计的选用提供合理和可靠的理论依据。

随着人们对产品质量概念的不断重视，农机产品消费者需求日趋主体化、个性化和多样化，基于产品和制造模式对此响应速度缓慢。吴昭同［8］指出现代全面质量管理要求将顾客需要的质量，通过主动设计过程集成到产品中并形成知识系统，以最大限度地满足顾客需要。结构可靠性优化设计与农机产品改进设计结合，不仅需按照生产质量标准还应融入用户的满意度来衡量。Yadaw等［9］针对设计开发的前期顾客需求，研究各种质量特性与质量损失之间的权衡问题；Duflou和Dewulf［10］基于公理设计理论和TRIZ理论，通过一系列特性矩阵分析解决设计参数间的耦合关系矛盾；杨帆和唐晓青［11］对面向质量设计的质量评估进行研究等。

本文以水稻摆栽机零部件设计为例，从顾客需求角度出发，基于关键质量特性指导，运用模糊回归理论优化质量功能配置与公理设计集成模型将顾客需求的模糊概念量化体现在产品的可靠性设计之中，使得产品设计符合市场需求。

1 关键质量特性的提取

关键质量特性（key quality characteristics， KQCs）概念源于顾客对产品质量的满意程度，是对产品设计质量进行有效控制的技术载体。质量功能配置（quality function deployment， QFD）是目前常用的一种设计质量控制技术，它产生于日本三菱重工对其产品可靠性的研究。随着工程设计的深入，设计过程的质量特性分为四个层次：产品级、设计级、制造级、装配级。本文研究的可靠性分析建模是基于零部件的设计参数，需提取制造级关键质量特性。顾客对于产品的抽象模糊需求属于产品级的认识，将顾客需求融入零部件可靠性优化设计转化成设计人员的设计语言需经历两层分析，本文运用模糊回归理论优化质量功能配置和公理设计（axiomatic design， AD）思想，对产品设计各阶段关键质量特性进行提取，集成模型如图1。

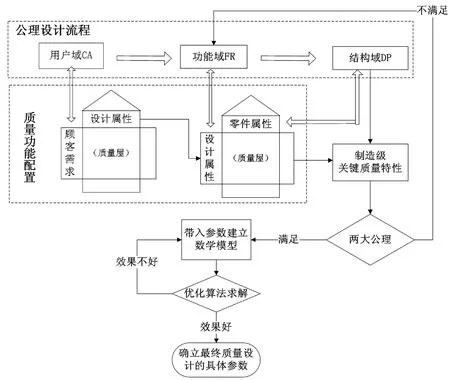
图1 质量功能配置与公理设计集成模型Fig. 1 QFD and AD integration model

运用集成模型提取关键质量特性的关键是根据顾客需求和工程特性之间的关系确定他们的相关性函数。QFD是由一系列的矩阵和图表将顾客需求转化为产品设计过程中质量特性和设计要求，通常矩阵信息之间的关系是模糊和不确定性，尤其是当顾客需求和工程设计特性数目较多的时候则更加困难。模糊回归理论［12］是对模糊、不确定关系建模的有效工具，为了更好的对QFD内部关系建模分析，本文利用该理论建立模糊规划模型，然后运用公理设计中功能域与结构域直接的“之”字映射关系，把某个功能与某个（些）结构对应起来，保证了设计质量满足顾客和市场需求［13］。

假设产品规划模型包含m个顾客需求、n个设计特性、l个产品。顾客需求矩阵记为R、设计特性矩阵记为F、产品矩阵记为C。ωi记为第i个顾客需求的Ri的权重、yi代表Ri的满意程度、xj代表Fj的目标值。模型规划是为了寻求一组X=（x1，x2，...，xn）使顾客满意度最大，即Vmax=（y1，y2，...，ym）。第i个顾客需求满意水平的模糊输出向量可表示为：

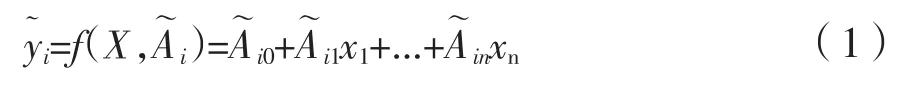
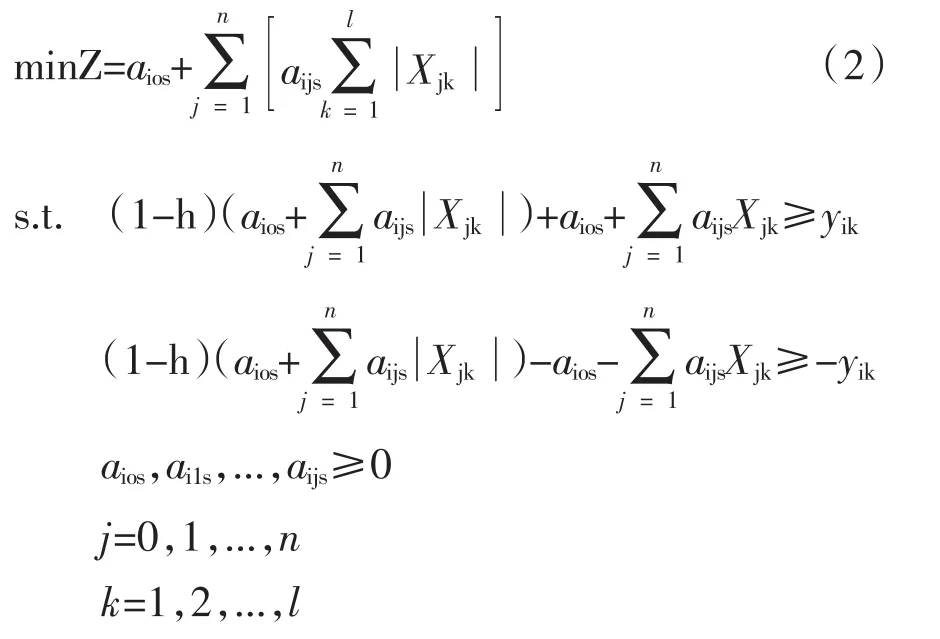
式中：aijc为模糊系数主值代表最有可能的取值，aijs为模糊系数展值代表偏离主值的波动范围，h为模糊线性参数估计的拟合度（相当于置信水平），且h∈（0，1）。

2 一种带约束的自适应粒子群算法

粒子群算法是Kennedy和Eberhart受到自然界中鸟群运动模式的启发提出了一种基于种群搜索的算法［14］。同其它算法相比，粒子群算法特征良好的全局优化能力，适合对复杂的结构进行求解。本文运用一种带约束的自适应粒子群算法（adaptive particle swarm optimization， APSO）对可靠性优化数学模型进行求解，具体对算法参数改进如下。

惯性权重的选择决定平衡全局搜素和局部搜索能力，分析指出一个较大的惯性权值有利于全局搜素，而一个较小的惯性权值更有利于局部搜索［15-16］。惯性权值在算法寻优过程中线性递减，能保证算法迭代的前期有较强的全局搜索能力，迭代后期进行更精确的局部开发。本文采取一种线性递减惯性权重，有效的平衡全局搜素和局部搜索能力：

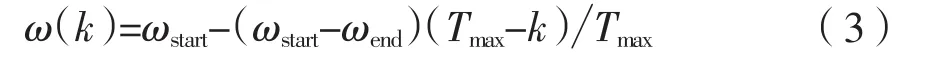
式中：ωstart为初始惯性权重，ωend为迭代中止惯性权重，Tmax为算法设置的迭代次数，k为当前迭代次数。

粒子群算法后期，几乎所有粒子都收敛于全局最小值或者局部最小值，此时粒子的多样性逐渐丧失，搜索速度降低，迭代效率不高［17］。有必要在粒子群算法中引入变异操作，对粒子适应度以一定的概率重新初始化，这样一来使得粒子能够跳出先前搜索到最优位置，在更大的空间开展寻优，同时保持了种群的多样性。本文引入一种自适应变异算子解决这个问题：

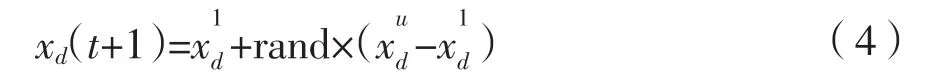
式中：xd

u为第d个粒子搜索空间的上限，xdl为第d个粒子搜索空间的下限，rand为区间［0，1］的随机数。

与一般粒子群算法不同，带约束的粒子群算法在进行运算的过程，种群粒子进行速度和位置初始化之后，以及在迭代过程中更新粒子速度和位置之后，都要通过约束条件判定，再将符合约束条件的粒子计算其适应度值。

3 基于关键质量特性的水稻摆栽机零部件设计

本文以水稻摆栽机的设计为例，首先对水稻摆栽机的客户需求与功能需求进行分析，构建质量屋（house of quality， HOQ）运用模糊回归理论分析提取设计级关键质量特性；然后通过公理设计中功能域（FR）与结构域（DP）映射关系，利用集成模型，得到制造级关键质量特性，即需要优化的零部件；最后建立可靠性优化设计数学模型及运用自适应粒子群算法求解。

3.1 水稻摆栽机零部件关键质量特性提取

本文从性能、结构设计、经济性、可靠性四个方面将水稻摆栽机顾客需求进行分析，矩阵表示R（i）=［性能，结构设计，经济性，可靠性］，其权重通过对水稻摆栽机的顾客反馈问卷获取，然后通过层次分析法相对权重比率及一致性检验法则求得；将功能要求矩阵表示F（j）=［模块化设计，机构运动，传动系统，机械系统同步性，控制系统，动力系统，作业对象及环境特性］；共选取同类3个产品进行竞争比较，其顾客需求竞争矩阵表示每一款产品的每项顾客需求，由农机产品的顾客反馈问卷获取，评分区间为［1， 5］；功能需求竞争矩阵的每一项代表每款产品的功能需求，由工程技术人员对不同产品进行分析获取，评分区间为［1， 5］。顾客需求与功能要求之间质量屋可表示图2。

由图2中可以看出每项顾客需求与哪些功能需求相关，利用式（1）和（2）进行模糊线性回归分析可得到QFD的规划模型，该模糊线性回归问题实际上是一个求解模糊回归系数的线性规划问题，其目标是要保证模糊幅度最小。根据Tanaka模型可知，hi≥ H，一般情况下取H ≥ 0.5。h的选择代表模糊数出现的可能性，利用式（1）和（2）建模取h=0.5，忽略展值的影响，可求得顾客需求矩阵及功能需求矩阵中各项因素模糊系数主值，所得计算结果见表1。

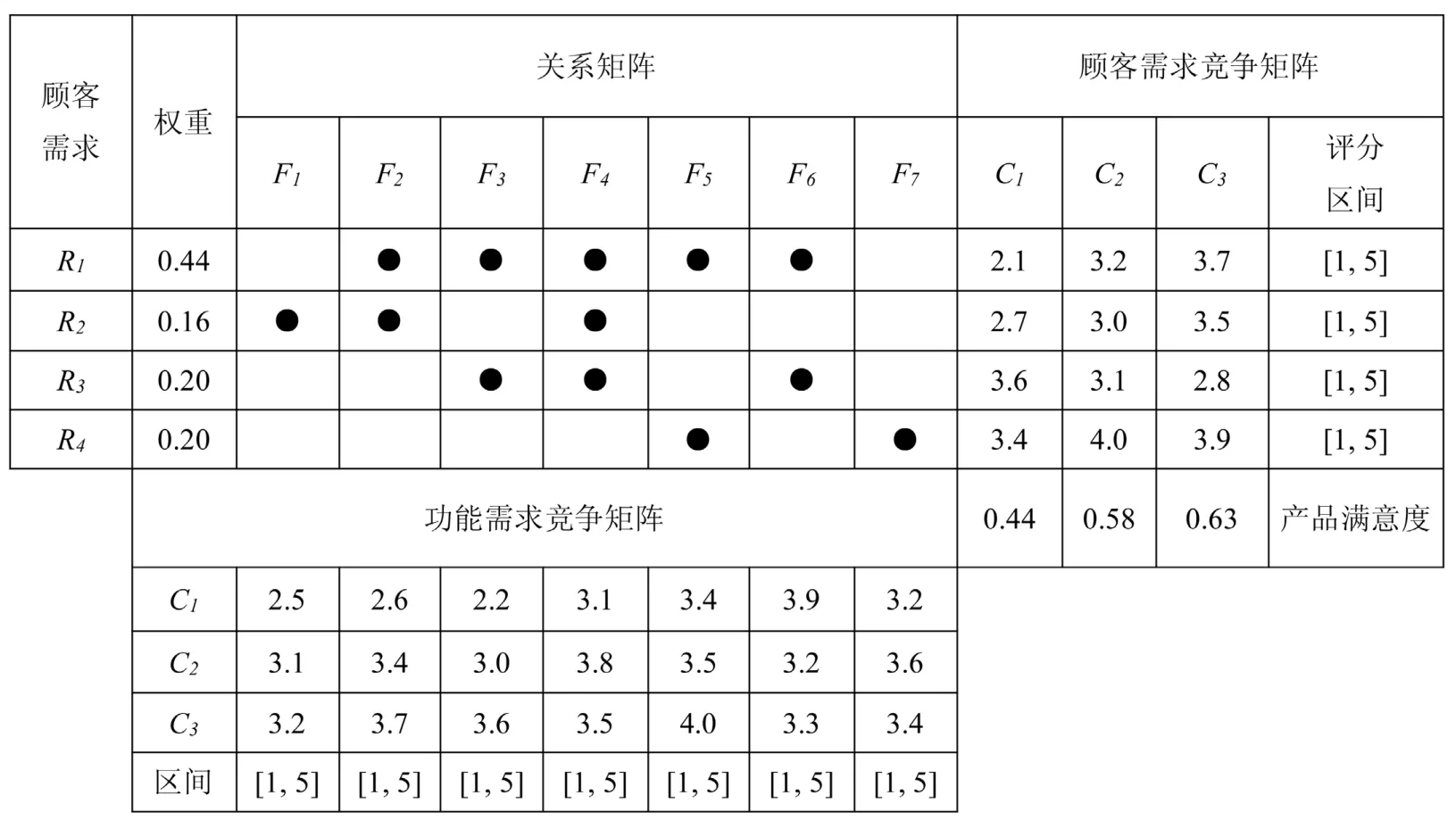
图2 水稻摆栽机顾客需求与功能要求质量屋Fig. 2 Rice transplanting machine HOQ of customer requirements and function requirements

表1 水稻摆裁机关联因素模糊系数主值求解结果Tblae1 Pice transplanting machine associated factors results of Fuzzy coefficient of principal value

采用1-5之间的数值表示产品各项指标的顾客满意水平，当yi=1时，V（yi）=0；yi=5时，V（yi）=1，不考虑模糊系数展值的影响，以顾客满意度最大化为目标的QFD数学模型为：

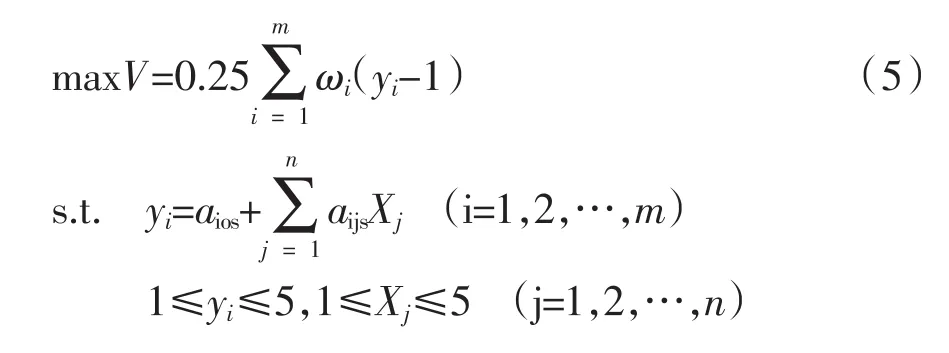
求解该模型可得到最终优化结果（表2）。

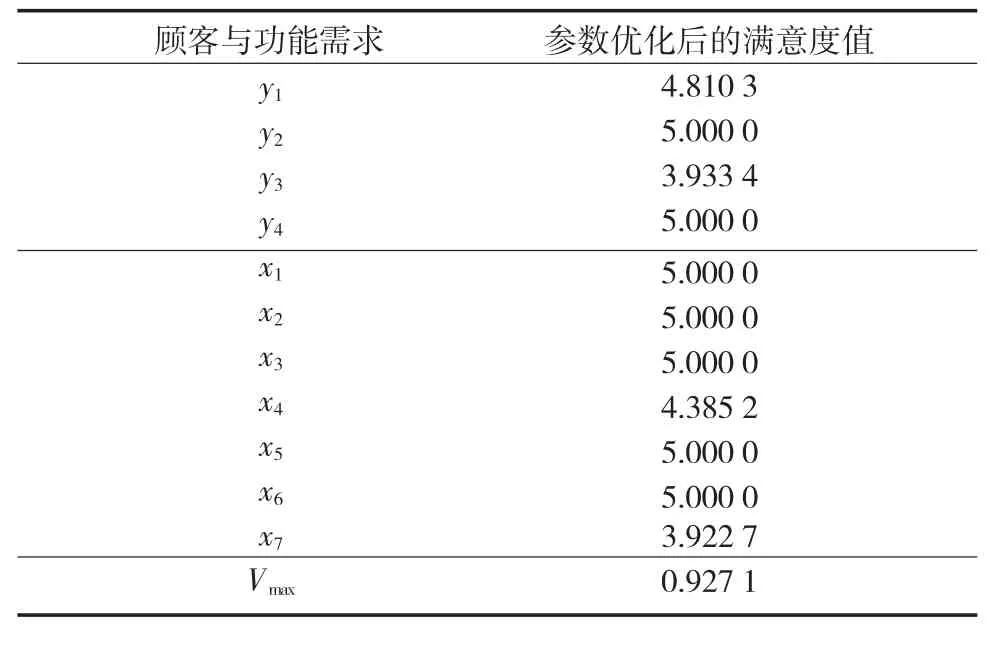
表2 参数优化结果Table2 The parameter optimization results

从表2可知，7个参数都需要进行不同程度的改进，而最后的顾客满意度可以达到0.927 1，远远超过用于比较的3个产品，而参数改进到最高分5为一种理想状态，相比较而言参数x4和x7的改进幅度较小，可以实现较好的结果，另外从相关矩阵中可以得出x4与y1、y2、y3均相关，对产品的顾客满意度影响较大。这里选取x4功能需求对应的水稻摆栽机机械系统同步性功能作为设计级关键质量特性进行下一步分析，利用公理设计域的映射分解。

图3是水稻摆栽机机械系统同步性功能（FR1）及其对应的机械结构（DP1）之间的映射关系。每层功能和结构都有下角标数字，功能依靠与之相对应的结构来实现。水稻摆栽机的总体结构（DP1）实现两个功能，即行走轮与摆栽机同步性（FR11）和摆栽机构自身的同步性（FR12）；秧苗与育秧盘分离（FR121）这一项功能是依靠顶秧杆曲柄滑块机构（DP121）来实现。这种“之”字映射关系，有效地将顾客重要的需求与产品本身的结构联系起来，使得水稻摆栽机接下来的优化设计重点得以体现。通过产品功能与结构的映射分析，本文选取水稻摆栽机的拨爪转动机构（DP123）为分析对象，将其设计要求矩阵表示，R（i）=［转位平稳，定位准确，承载能力，可靠性，可调性，结构复杂度，制造成本］，其主要结构零部件矩阵表示，F（j）=［拨盘，拨盘轴，轴承，拨爪］，再次运用质量屋模糊回归分析提取关键的结构零部件。所用方法与前文一致，由此得到的结论为拨盘轴对整个转动机构影响最大，拨盘轴的设计参数即零部件级关键质量特性，可靠性优化设计的对象即为拨盘轴的相关参数。

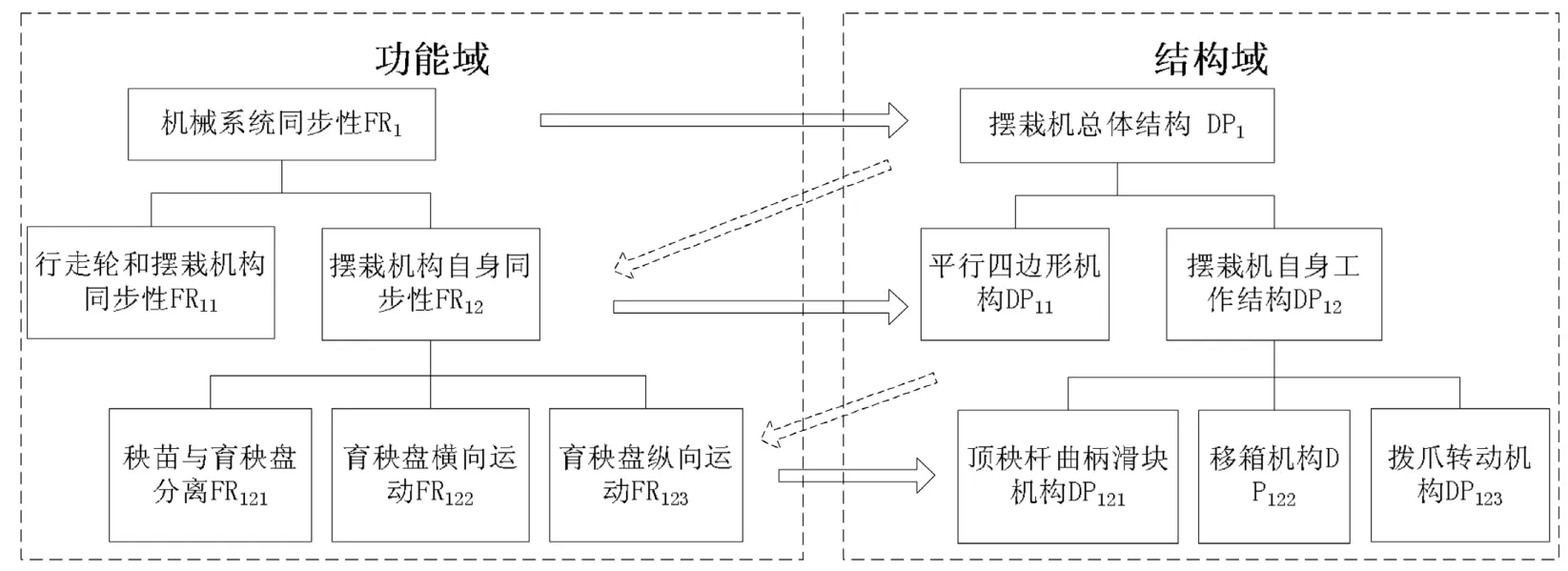
图3 功能域与结构域映射Fig. 3 Functional domain and Physical domain mapping

3.2 拨盘轴可靠性优化设计

水稻摆栽机拨盘轴是一截面形状为管形的空心传动轴，主要承受扭矩作用。已知拨盘轴设计扭矩（T）、材料的剪切弹性模量（G）及许用剪应力（［τ］）均服从正态分布，其均值和标准差分别为：T= （10 800， 480） N·mm，G=（81 000， 2 760） MPa，［τ］=（45，1.25） MPa；拨盘轴轴长L=713.5 mm为常数，单位长度许用扭转角［φ］=1.5 °/m，轴的可靠度为R0，拨盘轴的优化设计参数即为它的内外径名义尺寸。

本文的优化设计建模从质量、成本、可靠度方面考虑，把农机零部件的结构可靠度作为约束，设计变量X=［x1，x2］T=［d，D］T，约束条件分为强度约束、刚度约束和结构尺寸限制条件三种，由于拨盘轴的转速不大，这里忽略其转速条件及扭转失稳的情况。

1）强度约束：

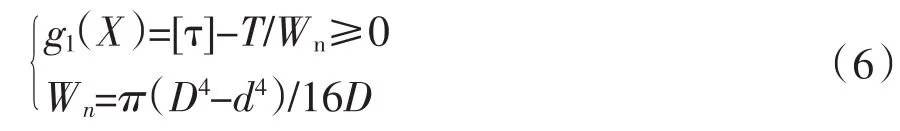
式中：T为轴受到扭矩，Wn为抗扭截面模量。

2）刚度约束：

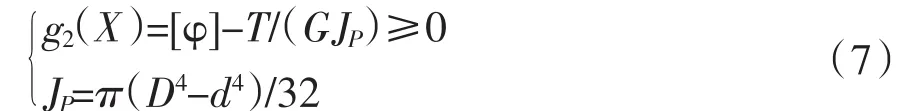
式中：Jp为极惯性矩。

3）结构尺寸限制条件：

优化模型将体积小、质量轻、低材料消耗的要求作为目标函数，问题描述为在满足上述约束条件下，拨盘轴的截面积最小。由于结构可靠性优化将设计参数当做随机变量来处理，进行可靠性建模首先需强度和刚度的概率性约束等价转换为确定型约束形式。根据应力—强度干涉理论［18］，以极限应力状态表示状态方程，采用一次二阶矩法对可靠性进行计算。综上所述，拨盘轴可靠性优化设计模型为：

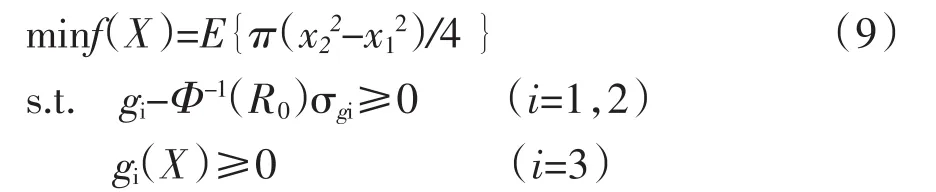
优化求解最后利用自适应粒子群算法对式（9）的可靠性模型迭代寻优，算法主要参数设置为粒子群种群规模为25，迭代次数为200，惯性衰减因子为0.95，随机变异概率为0.25。APSO算法分别计算了可靠度（R0）为0.995和0.999时拨盘轴截面积的适应度值，并得到了优化后的内外径名义尺寸。

当可靠度（R0）分别为0.995和0.999时，拨盘轴截面积最优值分别为135.815 mm2和139.907 mm2（图4）。为了检验计算结果的精度，运用Monte-Carlo模拟将拨盘轴的优化问题转化为基于正态分布的期望，然后随机抽取1 000个样本，对这些样本进行重复运算，统计分析落入失效区间的样本数，以失效事件发生频率近似代替失效概率，推导出服从正态分布的设计参数名义值。

在实际工程中Monte-Carlo方法常作为标准解来检验其他方法的准确性，表3给出了优化计算结果与样本数量为1 000的Monte-Carlo模拟检验结果，运用APSO算法求解的拨盘轴最优截面积同Monte-Carlo模拟检验结果相比其相对误差分别为2.53%和2.40%，可知APSO算法误差较小，有较高的计算精度。图4适应度曲线可知，APSO算法的收敛速度较快，图中折线反映自适应算子对粒子群寻优过程的影响，使其有一定概率跳出原有搜索位置，有效的保持了粒子群种群的多样性，提升了算法寻找更优值的可能性。

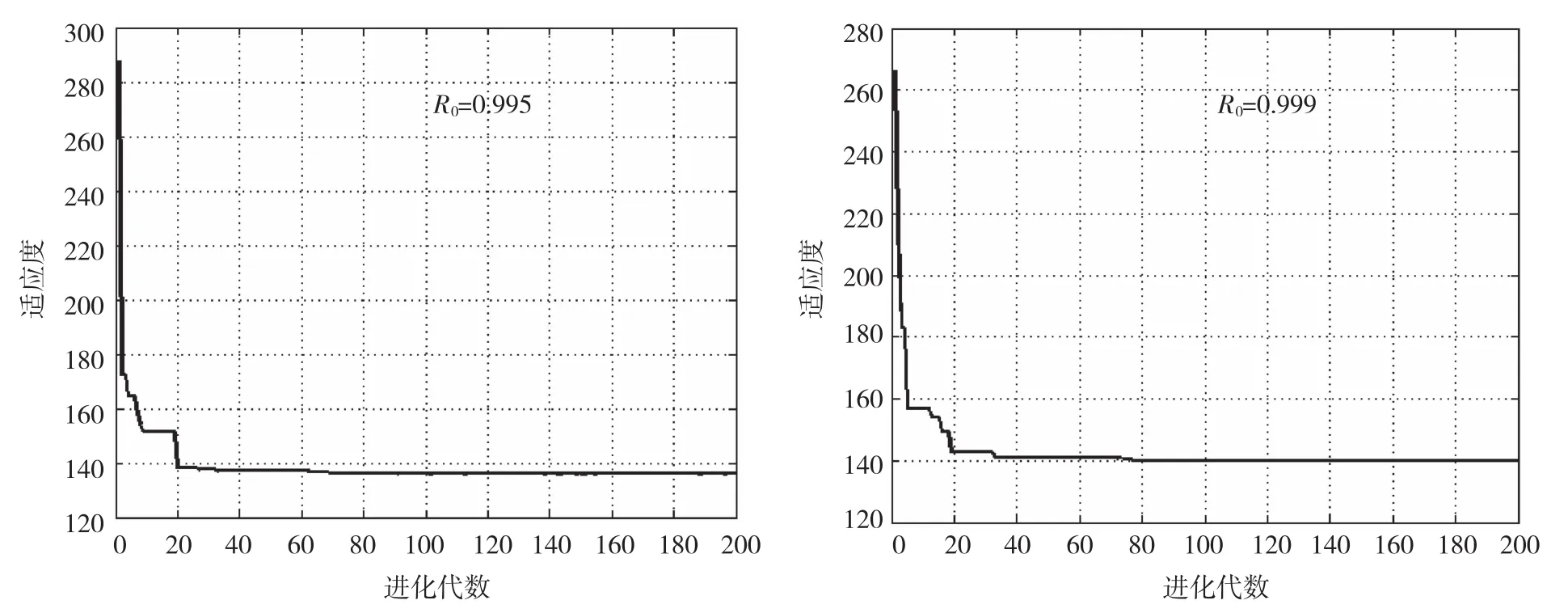
图4 目标函数适应度曲线Fig. 4 Fitness curve of the objective function

表3　APSO算法与Monte Carlo 对比Table3　APSO compared with the results of Monte Carlo

4 结论

本文从质量特性角度着手，将顾客需求与工程技术特性结合，利用质量功能配置、公理设计等工具对顾客需求的模糊要求进行QFD的模糊回归建模，使得农机装备产品设计过程更具指导性。并以水稻摆栽机为例，提取出水稻摆栽机拨爪转动机构拨盘轴的关键质量特性，将其进行可靠性建模，运用随机规划法将可靠性的概率型约束条件转化为确定型约束条件。

运用改进带约束的自适应粒子群算法对水稻摆栽机拨盘轴结构可靠性模型进行求解，分别计算了可靠度为0.995和0.999时的结构优化设计参数，并与Monte-Carlo检验比较，算法运算速度较快，效率高，结果精度较高，水稻摆栽机拨爪转动机构拨盘轴的最优截面积相对误差分别为2.53%和2.40%。实例验证了所提的方法和思路的指导性和可行性。

［1］ 张公绪. 新编质量管理学（第二版）［M］. 北京： 高等教育出版社， 2003. Zhang G X. New Quality Management （second edition）［M］. Beijing： Higher Education Press， 2003.

［2］ 农业部农业机械化管理司. 2012年全国农业机械化质量报告［M］. 北京： 中国农业科学技术出版社， 2013. The Department of Agricultural Mechanization Management in Ministry of Agriculture. The National Agricultural Mechanization Quality Report in 2012［M］. Beijing： Chinese Agricultural Science and Technology Press， 2013.

［3］ 罗锡文. 对加速我国农业机械化发展的思考［J］. 农业工程，2011， 1（4）： 2-8.Luo X W. Thoughts on accelerating the development of agricultural mechanization in China［J］. Agricultural Engineering，2011， 1（4）： 2-8.

［4］ Shapiro A， Dentcheva D， Ruszczyński A. Lectures on Stochastic Programming： Modeling and Theory［M］. SIAM， 2014.

［5］ 陈立周. 稳健设计［M］. 北京： 机械工业出版社， 2000. Chen L Z. Robust Design［M］. Beijing： China Machine Press，2000.

［6］ 王倩倩， 张义民， 张振先， 等. 齿轮系统随机振动及其传动误差的可靠性及灵敏度分析［J］. 东北大学学报（自然科学版），2011， 32（12）： 1741-1744. Wang Q Q， Zhang Y M， Zhang Z X et al. The reliability and sensitivity analysis of the gear random vibration system and transmission error［J］. Journal of Northeastern University （Natural Science）， 2011， 32（12）： 1741-1744.

［7］ Youn B D， Choi K K. Selecting probabilistic approaches for reliability-based design optimization［J］. AIAA Journal， 2004，42（1）： 59-67.

［8］ 吴昭同. 保质设计［M］. 北京：机械工业出版社， 2004. Wu Z T. Quality Design［M］. Beijing： China Machine Press， 2004.

［9］ Yadav O P， Bhamare S S， Rathore A. Reliability-based robust design optimization： A multi-objective framework using hybrid quality loss function［J］. Quality and Reliability Engineering International， 2010， 26（1）： 27-41.

［10］ Duflou J R， Dewulf W. On the complementarity of TRIZ and axiomatic design： From decoupling objective to contradiction identification［J］. Procedia Engineering， 2011， 9： 633-639.

［11］ 杨帆， 唐晓青. 基于特性关联的产品工程更改传播［J］. 北京航空航天大学学报， 2012， 38（7）： 1-8. Yang F， Tang X Q. Propagation of engineering change based on characteristic linkage perspective［J］. Journal of Beijing University of Aeronautics and Astronautics， 2012， 38（7）： 1-8.

［12］ Sener Z， Karsak E E. A combined fuzzy linear regression and fuzzy multiple objective programming approach for setting target levels in quality function deployment［J］. Expert Systems with Applications， 2011， 38（4）： 3015-3022.

［13］ Raharjo H， Xie M， Brombacher A C. A systematic methodology to deal with the dynamics of customer needs in quality function deployment［J］. Expert Systems with Applications， 2011， 38（4）：3653-3662.

［14］ Rackwitz R. Reliability analysis—A review and some perspectives［J］. Structural Safety， 2001， 23（4）： 365-395.

［15］ Zhang Y， Gong D， Sun X， et al. Adaptive bare-bones particle swarm optimization algorithm and its convergence analysis［J］. Soft Computing， 2014， 18（7）： 1337-1352.

［16］ 黄泽霞， 俞攸红， 黄德才. 惯性权自适应调整的量子粒子群优化算法［J］. 上海交通大学学报， 2012， 46（2）： 228-232. Huang Z X， Yu Y H， Huang D C. Quantum-Behaved particle swarm algorithm with self-adapting adjustment of inertia weight［J］. Journal of Shanghai Jiaotong University， 2012， 46（2）：228-232.

［17］ 郑永前， 张锦. 基于自适应粒子群算法的制造单元集成构建方法［J］. 计算机集成制造系统， 2010， 16（8）： 1666-1672. Zheng Y Q， Zhang J. Manufacturing cell integration formation method based on adaptive particle swarm optimization［J］. Computer Integrated Manufacturing Systems， 2010， 16（8）： 1666-1672.

［18］ Huang H， An Z. A discrete stress-strength interference model with stress dependent strength［J］. IEEE Transactions on Reliability，2009， 58（1）： 118-122.

（责任编辑：童成立）

Reliability-based optimization design of the agricultural machinery parts based on key quality characteristics

ZHOU Chen， LIN Wei-guo， ZHENG Xiang-zhou， XU Hong-mei
（College of Engineering， Huazhong Agricultural University， Wuhan， Hubei 430070， China）

Quality is an important factor in market competitiveness of the agricultural equipment. This paper quantifies the fuzzy concept of customer requirements and incorporates it into reliability design of the agricultural machinery parts， and presents a reliability-optimization method based on key quality characteristic. Firstly， the integration model of quality function deployment （QFD） and axiomatic design theory can be optimized by using fuzzy regression theory，and the key quality characteristics of each design phase of the agricultural machinery can be extracted. Secondly， guided by the reliability-optimization theory and stress-strength interference model， a mathematical model of the reliabilityoptimization design can be built based on key quality characteristics of agricultural machinery parts. Finally， the adaptive particle swarm optimization （APSO） algorithm with constraints is employed in the optimization analysis of the mathematical model. This paper analyzed the design process of key quality characteristics of rice transplanting machine's dial shaft， and respectively calculated the optimal design parameters when the reliability was 0.995 and 0.999. Compare to the Monte-Carlo test， the relative error of the dial shaft optimal cross-sectional area is 2.53% and 2.40%. The efficiency and effectiveness of the proposed analysis of the key quality characteristics are illustrated in the reliabilitybased optimization design of the agricultural machinery parts.

key quality characteristics； quality function deployment； fuzzy regression； reliability； particle swarm optimization

National Natural Science Foundation of China （51305152， 51405178）； The Fundamental Research Funds for the Central Universities （52902-0900206075）.

LIN Wei-guo， E-mail： linweiguo@mail.hzau.edu.cn.

04 May， 2015； Accepted 29 June， 2015

TH122

A

1000-0275（2016）02-0402-07

10.13872/j.1000-0275.2015.0110

国家自然科学基金项目（51305152，51405178）；中央高校基本科研业务费专项资金资助项目（52902-0900206075）。

周晨（1989-），男，湖北鄂州人，硕士研究生，主要从事现代农机装备设计制造及理论研究，E-mail： 397794895@qq.com；

林卫国（1978-），男，湖北武汉人，博士，讲师，主要从事现代农机装备设计制造及理论研究，E-mail： linweiguo@mail.hzau.edu.cn。

2014-05-04，接受日期：2015-06-29