基于点映射胞轨迹法的强非线性系统混沌演化与激变研究

杨庆超，孙方旭，柴　凯，李　爽

(海军工程大学 科研部,武汉　430033)



【基础理论与应用研究】

基于点映射胞轨迹法的强非线性系统混沌演化与激变研究

杨庆超，孙方旭，柴凯，李爽

(海军工程大学 科研部,武汉430033)

针对强非线性系统混沌演化与激变难以掌握，阻碍线谱混沌化技术工程化应用的问题，采用点映射胞轨迹法对强非线性系统的全局性态进行了研究；研究结果表明：随着激励力幅值的增加，系统经历了不止一次的对称破缺分岔，逆对称破缺分岔过程，系统通过不同形式由周期状态转变为混沌运动状态。

强非线性系统；点映射胞轨迹法；混沌演化；激变

低频线谱噪声在水中传播距离远，且频谱结构稳定，对水下航行器的声隐身性能构成了严重威胁。楼京俊等[1-3]提出当非线性隔振系统处于混沌运动状态时，其频谱为连续谱，可改变线谱频谱结构特征并削弱集中在线谱上的能量，达到隔振和削弱线谱强度的目的，即线谱混沌化控制方法。对于一个非线性隔振系统，该方法的关键在于充分认识非线性隔振系统通向混沌状态的道路，控制系统参数使非线性系统由周期状态进入混沌运动状态，且在外界环境改变时，使系统始终保持在混沌运动状态。另一方面，工程上一般通过施加反馈作用力实现对系统的主动控制，深入认识非线性隔振系统进入混沌运动状态的道路，为非线性隔振系统混沌化反控制奠定基础。本文针对强非线性系统，采用点映射胞轨迹法对其通向混沌的道路开展研究，为线谱混沌化技术实现工程化奠定基础。

1　强非线性隔振系统模型的建立

单自由度强非线性隔振系统如图1所示，其运动微分方程为

(1)

式(1)中，K1X+K3X3为非线性弹性回复力。

(2)

(3)

将式(2)和式(3)代入式(1)得

(4)

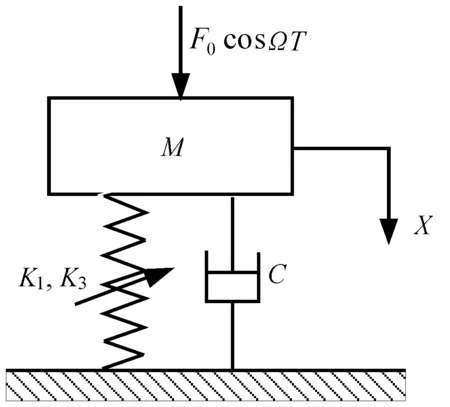
图1　非线性隔振系统

2　点映射胞轨迹法

采用数值方法研究强非线性系统的全局性态时，如果对一个初始条件积分，理论上经过充分长的时间后，系统的最终行为就确定了吸引子的位置，但该方法计算精度低且不实用。胞映射方法[4-6]认为，状态空间从理论上看是连续的，而实际上，所取的初始点无论如何都不能完全连续，若两点之间的初始距离为h，当所找的点与已知点的距离小于h，即可认为是同一点。胞映射方法的基本思想是把相空间离散为有限个胞，考察从每一个胞出发的胞轨道，最终便可确定由胞表示的吸引子及其吸引域。相比于一般的胞映射方法，点映射胞轨迹法增加了一个描述状态空间的尺度，并以此作为性态保持标准。在此条件下，点映射胞轨迹法比一般胞映射方法具有更好的计算精度和更好的经济性，其计算流程如图2所示。

图2　点映射胞轨迹法计算流程

3　强非线性系统混沌演化与激变

首先采用跟踪延拓法，即将 fk求得的解直接作为 fk+1= fk+Δf 时的初始计算条件，对随f变化时强非线性系统式(4)的全局形态进行计算分析，寻找一些系统吸引子性态发生变化的节点。

图3　非线性系统(4)在0.01≤f≤50区间变化的分岔图(ξ=0.1，ω=1.6)

参考非线性系统随激励力f变化的分岔图3，典型初始条件节点分区如下：

当0.24≤f≤0.87时，存在两个周期1解，且为大振幅和小振幅解，此时可采用谐波平衡法求出其响应曲线如图4所示；此时对系统采取认为干扰，将系统解控制在小振幅解上，对于系统的振动噪声控制具有重要意义。

图4　系统在区间0.24≤f≤0.87变化时振幅响应曲线

由上述分析可知，强非线性系统在区间0.01≤f≤50变化时，系统出现了两个混沌区间，第一个混沌现象是由周期1解通过对称破缺分岔及倍周期分岔形成，在此时混沌吸引子和周期3吸引子并存。第二个混沌现象是由周期3解通过对称破缺分岔及倍周期分岔形成，此时混沌吸引子充满了整个相平面。

4　总结

对于强非线性系统，如果想对全局性态进行较为精确的描绘，摄动法在多数情况下都不再适用，此时通过点映射胞轨迹法分析非线性系统的全局性态可以得到较为理想的结果。针对的强非线性系统，由分析结果可知，随着激励力幅值的增加，系统行为十分复杂，通往混沌的过程不能被简单的归结为对称破缺分岔—倍周期分岔—混沌的过程，随着激励力幅值的增加，系统经历了不止一次的对称破缺分岔，逆对称破缺分岔等过程。

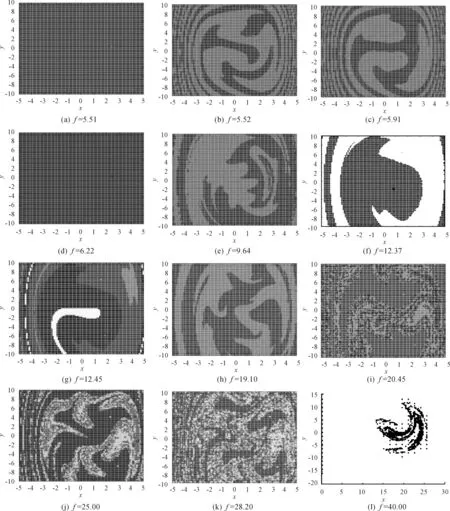
图5　强非线性系统在不同f下的点映射胞轨迹图

[1]LOU Jingjun,ZHU Shijian,HE Lin,et al.Application of Chaos Method to Line Spectra Reduction[J].Journal of Sound and Vibration.2005,286:645-652.

[2]YU Xiang，ZHU Shijian，LIU Shuyong.A New Method for Line Spectra Reduction Similar to Generalized Synchronization of Chaos[J].Journal of Sound and Vibration.2007,306:835-848.

[3]张振海，朱石坚，楼京俊.基于离散混沌化方法的线谱控制技术研究[J].振动与冲击，2010,29(10)：52-56,126.

[4]徐伟，贺群，李爽．基于复合胞化空间的图胞映射方法[J]．物理学报．2008，57(7)：4021-4029．

[5]杜度，张纬康，毕毅，等.系泊海洋平台周期运动倍周期分岔的胞映射分析[J]．应用力学学报，2004，21(4)：71-78．

[6]徐伟，孙春艳．胞映射方法的研究和进展[J]．力学进展．2013，43(1)：91-100.

(责任编辑唐定国)

StudyonEvolutionandCrisisofChaosAttractorinStronglyNonlinearSystemBasedonPMUCRMethod

YANGQing-chao,SUNFang-xu,CHAIKai,LIShuang

(OfficeofResearch&Development,NavalUniversityofEngineering,Wuhan430033,China)

Fortheproblemthatitisdifficulttograsptheevolutionandcrisisofthechaosattractorinstronglynonlinearsystem,andtheengineeringapplicationofthelinespectrachaotificationwasobstructed,andtheglobalbehaviorofthestronglynonlinearsystemwasstudiedbasedonPMUCRmethod.Theresultshowsthattherearemorethanoncesymmetrybreakingbifurcationandinversesymmetrybreakingbifurcationprocessandtheroadsturningintochaosarevarious.

stronglynonlinearsystem;PMUCR;chaosevolution;chaoscrisis

2016-04-15；

2016-05-18

国家自然科学基金青年科学基金资助项目“准零刚度隔振系统混沌化技术研究”(51509253)和“潜艇机械设备混沌振动自适应预测控制研究”(51579242)

杨庆超(1987—)，男，博士，主要从事噪声与振动控制研究。

10.11809/scbgxb2016.09.032

format:YANGQing-chao,SUNFang-xu,CHAIKai,etal.StudyonEvolutionandCrisisofChaosAttractorinStronglyNonlinearSystemBasedonPMUCRMethod[J].JournalofOrdnanceEquipmentEngineering,2016(9):138-141.

TJ451

A

2096-2304(2016)09-0138-04

本文引用格式：杨庆超，孙方旭，柴凯，等.基于点映射胞轨迹法的强非线性系统混沌演化与激变研究[J].兵器装备工程学报，2016(9):138-141.