多用户MIMO系统中基于博弈论的鲁棒性功率分配
董作霖
(河南工学院 教务处,河南 新乡 453003)
多用户MIMO系统中基于博弈论的鲁棒性功率分配
董作霖
(河南工学院 教务处,河南 新乡 453003)
针对多用户多输入多输出(MU-MIMO)天线系统,提出了一种基于非合作博弈论的功率分配方案。此博弈模型中,以用户在系统中的信号泄漏噪声比值(SLNR)作为用户功率分配和公平性参数设置的依据,保证用户所期望的服务质量和公平性,并证明了纳什均衡的存在性。其次,考虑信道估计误差的影响,提出了一种基于滑动模型的迭代功率分配控制算法满足所有用户的最小通信质量要求。仿真结果显示此方案在信道误差的情况下,相比现有方案可提高系统吞吐量。
多用户多输入多输出;功率分配;博弈论;信号泄漏噪声比;纳什均衡
1 引 言
多用户多输入多输出(Multi-UserMultiple-InputMultiple-Output,MU-MIMO)天线技术在提高系统容量和频谱效率方面具有明显的优势,但它也存在用户间同频干扰(Co-ChannelInterference,CCI)的问题。如何抑制MIMO下行链路中的噪声干扰和同频干扰是多用户MIMO技术的研究重点。
用户功率分配和预编码技术(例如:信号泄漏噪声比值(Signal-to-Leakage-and-NoiseRatio,SLNR))能够提升MIMO系统的性能,近几年来已经被广泛地研究。文献[1]提出了一种最大化用户SLNR的功率分配算法。文献[2]着重研究了在MU-MIMO下行链路中,基于SLNR预编码动态功率分配方案。为降低功率分配算法的复杂度,文献[3]提出了一个次优化的功率分配方案。文献[4]提出了两个功率分配方案,通过利用用户的SLNR值和天线关联性的信息,来设计最优功率分配算法,进而最大化系统吞吐量。此外,考虑接收滤波器和发射滤波器的功率分配,文献[5]提出了一种基于修改SLNR预编码准则的方案,设计在用户终端有效使用和评估接收机的子空间方法。然而,以上研究均未能考虑到信道估计误差对MU-MIMO系统的影响,忽略了用户间的最小通信质量要求。
博弈论被越来越多人认为是解决通信资源分配问题的一种有效数学工具。为在博弈论框架内制定问题,考虑到信道的不确定性以及无法准确地获得信道状态信息,文献[6-7]提出了一种鲁棒功率分配方案,该方案源于博弈论架构思想,提供了两种充分条件下的数学结构来使系统的整体效率达到最大且保证纳什均衡。博弈论解决资源分配的方案已被逐步应用于MIMO系统中优化资源管理。然而,以上文献虽然能够提高方案的鲁棒性,但是却忽略了用户之间功率分配的公平性。
在非合作动态控制博弈模型(NoncooperativeDynamicPowerGamePolicy,NPGP)中,本文通过利用各用户的SLNR值被用于惩处价格的参考指标,以保证MU-MIMO系统中用户之间的QoS和公平性。受信道评估误差的影响,发射机不能精确分配可用资源来满足用户的服务质量,纳什均衡也无法得到有效保证。为了解决这一问题,在NPGP模型基础上通过分析博弈理论在无线系统的应用,本文提出一种基于SLNR预编码MU-MIMO系统非合作博弈理论的动态功率分配方案,并借用滑模型来增强系统的鲁棒性,保证用户的公平和通信质量要求。
文中符号说明:E[·]表示期望;(A)H、det(A)和Tr(A)分别表示矩阵A的共轭转置、行列式和矩阵A的迹;IMk表示Mk×Mk单位矩阵。
2 系统模型
本文以同时存在N个发射机天线和K个用户的MU-MIMO下行链路为系统模型。第k用户用Mk为接收天线,系统模型如图1所示。
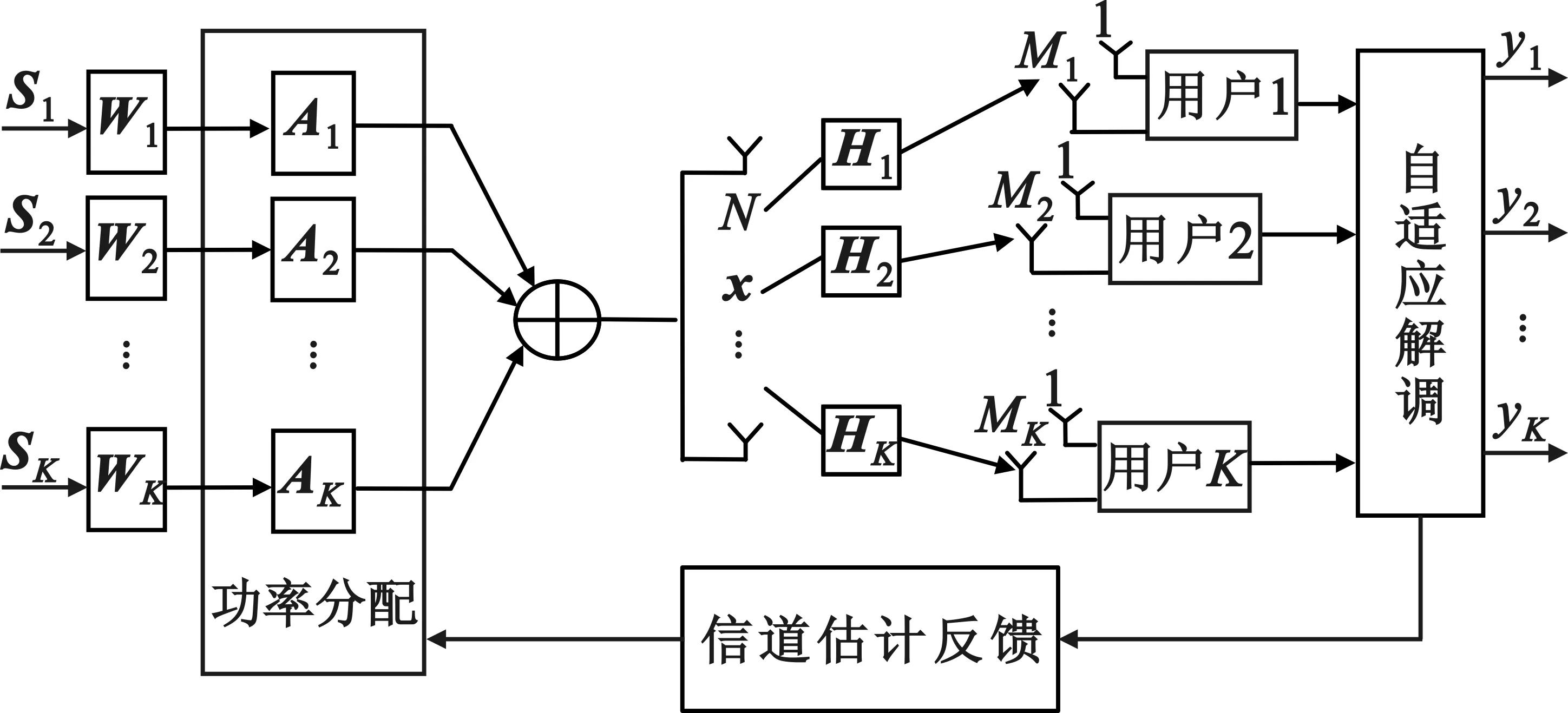
图1MU-MIMO下行链路系统模型
Fig.1MU-MIMOdownlinksystemmodel
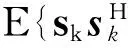
xk=WkAksk。
(1)
式中:Wk=[wk,1,wk,2,…,wk,Mk]∈N×Mk是用户k的预编码矩阵;wk,j表示第k个用户的第j个信息流的预编码矢量。预编码矢量是统一标准化的,即‖Wk‖2=1(k=1,2,…,K),那么)=Mk。所有用户总的发射功率


对于移动用户k,Mk×1接收信号可以表示为

(2)
式中:第二项表示CCI;加性噪声矢量nk被假定为独立同分布(IndependentandIdenticallyDistributed,IID),其均值为零,方差为δ2,表示为CN(0,δ2)。
根据信号泄露的概念[1],从用户k到其他所有用户的平均信号泄露功率为
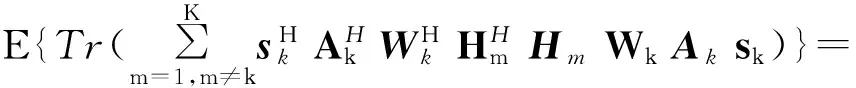
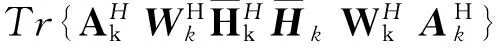
(3)
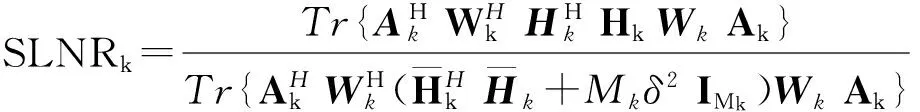
(4)
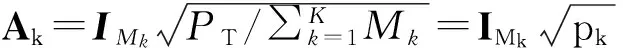
经典SLNR方案给每个用户设定等功率分配[2],源于以下通过每个用户的最大SLRN的独立优化问题:
Wk=argmaxSLNRk=

(5)

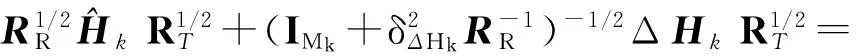

(6)
因此,用户k的SLNR可修改如下:

(7)
3 基于最优CSI博弈论的动态功率分配
考虑到MU-MIMO系统中用户之间的公平性,寻找一个最佳功率分配策略力求提高所有被服务用户的通信质量至关重要。基于以上需求本节提出一种可行的非合作博弈动态功率控制方案解决功率控制问题。
3.1非合作功率控制博弈模型
本文用博弈论来分配在SLNR预编码MU-MIMO系统中各用户的功率,并且把SLNR值作为设置用户价格因子的参考依据。通过将功率控制问题定义为非合作博弈来解决功率控制问题:
G={K,{Pk},{Uk(·)}} 。
式中:k= [1,2,3,…,K]是参加移动用户(选择特定功率来发射的决策者);Pk表示用户k的策略功率分配值;Uk(·)是策略中移动用户k的应用功能。
每一个加入的移动用户可以在功率矢量空间P={p1,p2,p3,…,pK}选择功率pk∈PK。所有移动用户通过选择功率分配空间策略得到一组竞赛结果。用户k实用功能是Uk(pk,P-k),P-k是除用户k以外的所有用户功率矢量,每个用户的目标仅仅是使自己的实用功能最大化。为选择最佳的发射功率空间策略并增强其实用性,非合作博弈模型[3]可被定义为
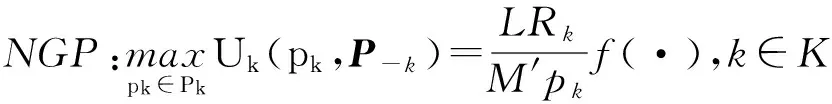
(8)
式中:L和M′分别是信息比特数和一个数据包的总比特数;Rk是用户k的传输率;γk代表用户k的信号泄漏噪声比SLNRk。式(8)中,f(·)是效率函数,假定呈sigma形状函数[6],f()=1,f(0)=0以保证当pk=0时,Uk=0。效率函数f1(γk)=(1-e-γk/2)M,受sigmal函数启发,为降低实际执行中复杂度,我们定义效率函数为f2(γk)=1/(1+e10-γk)。如果γk用在传统的MIMO系统中,该函数将非常接近于f1(γk),它与用户的信号泄漏噪声比值有关并且可以忽略接入技术中的调整率。
式(8)表明SLNR值高的用户在实用功率分配方案之前可能获得更多的收益[7],但NPG的纳什均衡点是无效的,这是由于用户的自我优化行为会降低系统性能。惩罚因子就是通过鼓励用户用更为有效的代价函数(分散决策适合整个系统)来有效地使用系统资源,所以,非合作功率控制博弈模型提供了如下一种更好的功率分配控制方案:

(9)
式中:Ck:P→R+是第k个用户的定价公式;ck(pk,P-k)=μλkepk,λk表示第k个用户的惩处参数,μ是惩处参数的价格权数。一般状况下不同用户依据其自身特性将会设定不同的价格惩处参数,这点与其他研究中普通的定价方案不同,进而NPGP定价模型可表示为
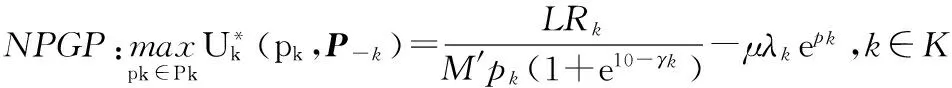
(10)
定价函数是接收功率的非线性函数,这样对其他用户的干扰便能得到更好的吞吐性能。因此,我们采取自适应定价方案,根据综合干扰,不同用户λk随之改变。价格惩处参数λk可以表示为

(11)
式(10)和式(11)证明了拥有高效用水平的用户具有更高的SLNR值(好的信道情况)且该类用户接收了最大效用并被分配更低的发射效率,但拥有更低效用的用户拥有更低的SLNR值(差的信道情况)并且使用更高的功率发送。为使效用达到最大,拥有更高SLNR值和干扰的用户惩处参数应该被严格控制,被收取高价的用户将合理地降低其发射功率。
3.2纳什均衡的存在性
根据帕尔提丝理论不动点定理(Topkis Fixed Point Theorem),所有超模博弈游戏至少有一个纳什均衡点[8-10],所以本节只需证明非合作博弈G=[K,{Pk},{uk(·)}]是一个超模博弈。根据文献[8],超模博弈中所有实用功能的参与者应该满足以下两个条件:一是所有参与者的策略空间集合;二是效用函数二次导数的值不小于零。

显然G=[K,{Pk},{uk(·)}]满足超模博弈的第一个条件,因为每个用户的策略空间Pk∈[pmin,pmax]。本文提出的NPGP方案和文献[5]相似,而文献[5]已证明了该方案可以提高帕累托最优,所以,此处只需验证该方案满足第二个条件。由公式(8)可得NPGP的二阶功率导数为
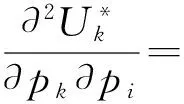

(12)
γk的一阶功率导数为

(13)
式中:Gk是用户k从BS获得的链路增益。
根据γk,效率函数f(γk)的二阶SLNR导数为

(14)

4 鲁棒功率分配
为确保在信道估计误差情况下所有用户都享有QoS的最低要求,本节在NPGP方案中采用一种迭代算法的滑模模型为每个用户分配总发射功率,进而为保证所有用户的最小QoS要求提出一种优化算法。
4.1基于滑模模型的鲁棒功率分配
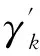
步骤1n=0时以及最初的功率传输数组P(n)=(p1(n),p2(n),…,pK(n))。

步骤3使用滑动模型,使传输功率控制器对信道的不确定性达到鲁棒并且达到所有用户的QoS要求。
(1)计算滑动过程中用户当前的信号泄漏噪声比和最小信号泄漏噪声比之差Sk以及用户的李雅普诺夫函数Vk:
(15)
(2)采取以下方程:

(16)

步骤4获取通过NPGP方案的传输功率数组P(n)。
步骤5如果所有用户满足条件
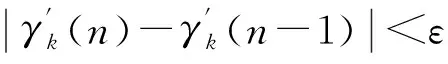
然后停止算法或者返回至步骤2,获取传输功率数组P(n)是所有用户的最优分配数组。
根据前文的证明过程,该算法可以得到最后的NE点,并获得分配数组中带有不完全信息的P(n)信道估计误差最优功率。
4.2复杂度分析
如果按照传统的注水迭代算法来更新功率,所需要的复杂度是O(L×M×N×K2),其中L是迭代次数。本文采用了滑窗模型的ε-最小门限迭代算法求解,其求解功率复杂度为O(M×N×K2·lb(ε-1))。可以看出本文提出的方案的复杂度和系统中发射接收天线有关,而且用户数目对其复杂度的影响较大。另外,迭代过程中ε的取值也影响着算法复杂度。
5 仿真结果及性能分析
本节我们将通过仿真验证本文所提方案的性能,仿真中假设M1=M2=…=MK=M,即接收天线数和用户数相同。用m表示每个用户的数据流量且假定每个用户数据流量相同。
通过以下4种方案对比验证本文方案的性能:
(1)文献[3]中提出的基于SLNR预编码功率分配(SLNR-PA)方案;
(2)文献[4]中提出的最大SLNR预编码功率分配(M-SLNR-PA)方案;
(3)信道估计误差条件下的非合作功率控制博弈(SNLR-NPGP)基础上提出的预编码功率分配方案;
(4)本文在信道相关和信道评估误差情况下基于非合作功率控制博弈(R-SLNR-NPGP)提出的SLNR预编码功率分配方案。
本文中所有的仿真都在瑞利衰落信道环境中,且使用QPSK进行调制。假定参数R=104b/s,M′=80 b,L=64 b,ε=10-2,μ=50 000,G=100,对所有用户都适用。结果显示平均超过5 000个信道都满足该曲线,每个信道实现的相干时间包括每个用户200符号周期。SNR定义为每个天线期望接收的功率和噪声功率之比PT/δ2,信道评估误差是高斯分布随机生成的。

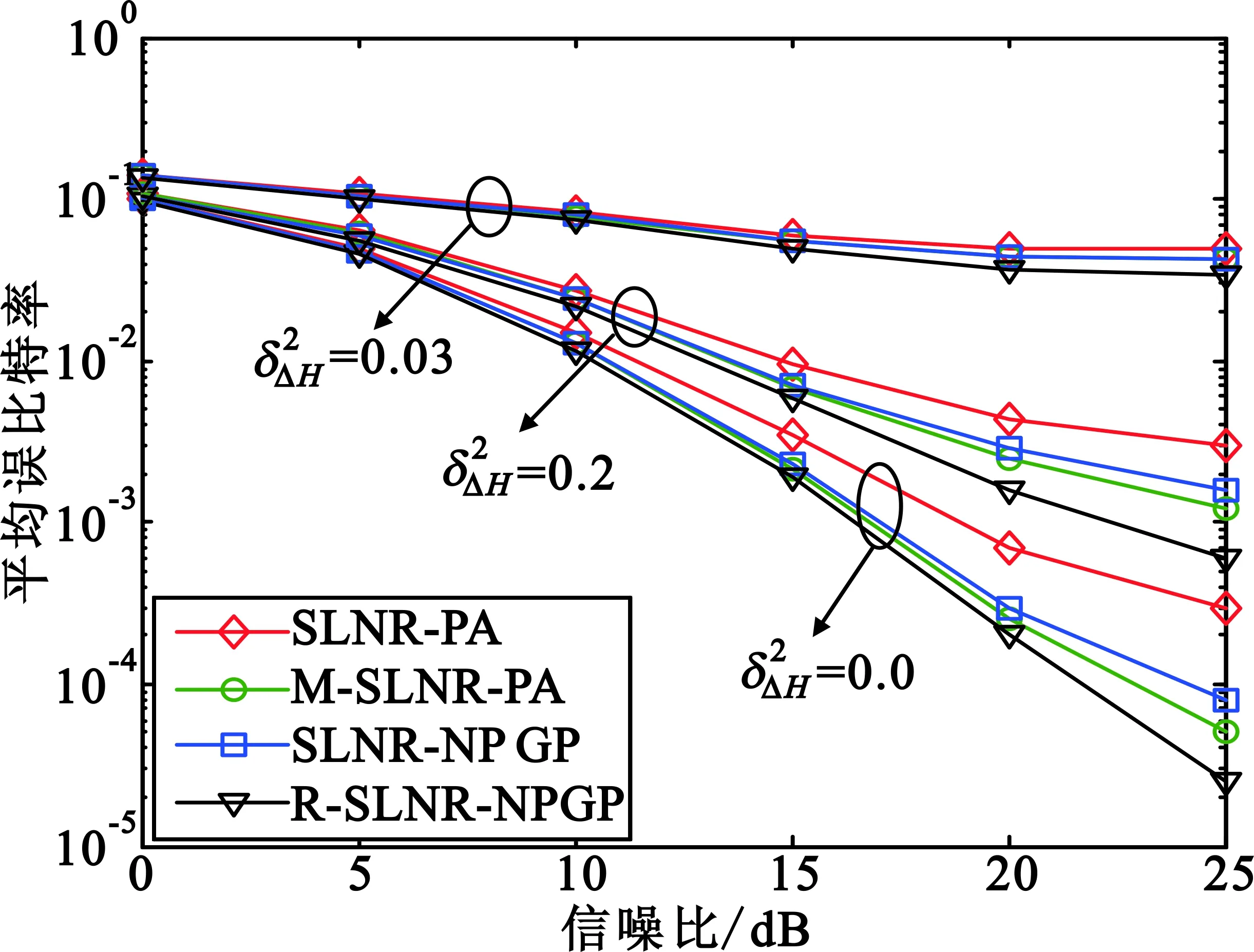
(a)BER

(b)吞吐量
图24种方案的BER性能和吞吐量比较
Fig.2 Comparison of BER performance and throughput among four schemes
6 结束语
本文阐述了在SLNR预编码MU-MIMO系统中存在信道估计误差情况下的一种功率分配方案。该方案通过每位用户的SLNR值作为惩处价参考进而控制功率分配值来保证系统中用户间的公正性,减少用户之间的干扰。考虑信道不确定性带来的影响后,提出采用滑动模型的迭代算法来满足用户所要求的服务质量。仿真结果说明该方案相比现有方案可提高系统的吞吐量。然而,本文所提出的方案是在小规模的MIMO系统中,且服务的用户数目不是很多。在未来可以考虑到在第五代移动通信系统中的较多用户资源分配的问题,比如:在大规模MIMO系统和超多用户的网络中如何构建低复杂度的功率博弈分配方案等。
[1]魏飞,杨震. 基于博弈论的MIMO认知无线电波形自适应算法[J].电子学报,2011,39(10):2269-2276.
WEI Fei,YANG Zhen. An adaptive algorithm for MIMO cognitive radio based on Game Theory[J].Acta Electronica Sinica,2011,39(10):2269-2276.(in Chinese)
[2]ZHANG Bijun,ZHAO Songyi.A robust DL MU-MIMO algorithm and UE specific SINR compensation mechanis in LTE-A[J].电讯技术,2015,55(9):984-992.
ZHANG Bijun,ZHAO Songyi.A robust DL MU-MIMO algorithm and UE specific SINR compensation mechanis in LTE-A[J].Telecommunication Engineering,2015,55(9):984-992.(in English)
[3]吴学文. 基于Khatri-Rao积的3D MU-MIMO预编码方法[J].电讯技术,2014,54(11):1510-1515.
WU Xuewen.3D MU-MIMO precoding method based on Khatri-Rao product[J].Telecommunication Engineering,2014,54(11):1510-1515.(in Chinese)
[4]WANG J J,XIE X Z. Dynamic power allocation based on SLNR precoding for multiuser MIMO downlink[C]//Proceedings of 4th International Conference on Wireless Communication,Networking and Mobile Computing.Dalian:IEEE,2008:1-4.
[5]李瑛,詹伟,王晓燕,等.多用户MIMO系统广播信道的连续块对角化预编码算法[J].电讯技术,2014,51(4):40-43.
LI Ying,ZHAN Wei,WANG Xiaoyan,et al.Successive block diagonalization pre encoding algorithm for MU-MIMO broadcast channels[J].Telecommunication Engineering,2014,51(4):40-43.(in Chinese)
[6]CHEN J,SWINDLEHURST A L.Applying bargaining solutions to resource allocation in multiuser MIMO-OFDMA broadcast systems[J].IEEE Journal on Selected Areas in Communications,2012,6(2):127-139.
[7]兰星,王兴亮,李伟,等.基于Stackelberg博弈的多输入多输出雷达信号与目标干扰优化[J].计算机应用,2015,35(4):1185-1189.
LAN Xing,WANG Xingliang,LI Wei,et al.Multi-input multi-output radar signal and target jamming optimization based on Stackelberg game[J].Journal of Computer Applications,2015,35(4):1185-1189.(in Chinese)
[8]PATCHARAMANEEPAKORN P,DOUFEXI A,ARMOUR S M D.Weighted sum capacity maximization using a modified leakage-based transmit filter design[J].IEEE Transactions on Vehicular Technology,2013,62(3):1177-1188.
[9]钟卫,徐友云.多用户MIMO系统中的一种基于博弈论的功率控制[J].电子与信息学报,2006,28(8):1368-1372.ZHONG Wei,XU Youyun.Power control based on game theory for MIMO system[J].Journal of Electronics and Information Technology,2006,28(8):1368-1372.(in Chinese)
[10]KULKARNI V V,BISWAS J,LIU R P,et al.Robust power allocation for mimo beamforming under time varying channel conditions[C]//Proceedings of 2011 IEEE 73rd Vehicular Technology Conference.Budapest,Hungary:IEEE,2011:5-8.

董作霖(1970—),男,河南新乡人,1992年于北京理工大学获工学学士学位,2004年于西安交通大学获工程硕士学位,现为河南工学院副教授,主要研究方向为通信系统、无线传感器网络。
DONG Zuolin was born in Xinxiang,Henan Province,in 1970. He received the B.S. degree from Beijing Institute of Technology and the M.S. degree from Xi′an Jiaotong University in 1992 and 2004,respectively. He is now an associate professor. His research concerns communication system and wireless sensor network.
Email:dongzuolin@163.com
RobustPowerAllocationBasedonGameTheoryforMulti-userMIMOSystems
DONGZuolin
(OfficeofAcademicAffairs,HenanInstituteofTechnology,Xinxiang453003,China)
Thispaperpresentsapowerallocationschemebasedonnon-cooperativeGametheoryformulti-usermulti-inputmulti-output(MU-MIMO)antennasystems.Thegameschemeusesthesignal-to-leakage-and-noiseratio(SLNR)ofusersinthesystemasaguideofpowerallocationandfairnessparametersetting,furthermoreestablishesagamemodeltoensureusers’QualityofService(QoS)andfairness,aswellasprovestheexistenceofNashequilibrium(NE).Secondly,consideringtheinfluenceofchannelestimationerror,itproposesaniterativealgorithmbasedonslidingmodeltoupdateallocatedpowerinordertomeettheminimumQoSrequirementsamongallusers.Simulationresultsshowthattheschemecanimprovethesystemthroughputcomparedwiththeexistingschemesinthepresenceofchannelerror.Keywords:MU-MIMO;powerallocation;gametheory;signal-to-leakage-and-noiseratio;Nashequilibrium
10.3969/j.issn.1001-893x.2016.09.012
2015-12-08;
2016-05-16Receiveddate:2015-12-08;Reviseddate:2016-05-16
TN929.5
A
1001-893X(2016)09-1017-06
引用格式:董作霖.多用户MIMO系统中基于博弈论的鲁棒性功率分配[J].电讯技术,2016,56(9):1017-1022.[DONGZuolin.Robustpowerallocationbasedongametheoryformulti-userMIMOsystems[J].TelecommunicationEngineering,2016,56(9):1017-1022.]
**通信作者:dongzuolin@163.comCorrespondingauthor:dongzuolin@163.com

