电力拖动系统稳定性仿真分析
张彦南 王旭

【摘 要】为设计出能够实现稳定的电力拖动系统。结合某一个设计案例,建立了系统的数学模型,在设定阶跃信号输入后,进行稳定性仿真。通过调整增益值,得到了良好的系统动态特性,为后续电力系统的优化,奠定了基础。
【关键词】电力拖动系统;稳定性;增益值
Stability Simulation Znalysis of Electric Drive System
ZHANG Yan-nan1,2 WANG Xu3
(1.Sichuan University, Chengdu Sichuan 610065, China;
2.Dazhou Municipal Development and Reform Commission, Dazhou Sichuan 635000, China;
3.Chengdu college of university of Electronic Science And Technology of China, Chengdu Sichuan 611731, China)
【Abstract】Designed to achieve a stable electric drive system. Combined with a design case, the mathematical model of the system is established, and the stability simulation is carried out after the input of the step signal. By adjusting the gain value, good dynamic characteristics of the system are obtained, which lays the foundation for the optimization of the power system.
【Key words】Electric drive system; Stability; Gain value
电力拖动系统[1],是集电机能量转换、生产机械运转于一体的有机整体。随着电机拖动技术的飞速发展,实现系统的自动控制,已经成为了趋势。如此一来,系统的控制效果、动态性能以及稳定性等指标优良与否,是设计中必须考虑的问题。因此,当系统完成设计后,对其动态性能和稳定性进行仿真,能够有效预判系统的整体性能,并根据情况,优化增益值,保证系统的性能优越。综上所述,本文结合一个电力拖动系统的案例,建立了系统的数学计算模型,并完成仿真。最后,获得了系统的动态运行规律,再改变参数,让该系统的性能参数,达到了良好的指标。
1 系统结构分析
在电力拖动系统数学模型建立之前,首先要做的就是进行结构分析。以明确数学模型的具体模块。从电机启动到稳定运行,一般会经历两个阶段:(1)系统振荡阶段;(2)稳态稳定运行阶段。通常情况下,稳定运行的系统,不会出现太大的问题。而振荡频繁的动态阶段,则是表征其性能的关键。因此,仿真过程,仅需针对动态特性即可。从系统的自动控制元件来看,主要包括:给定元件、信号元件、反馈元件等,部分元件为:
(1)三相电源,频率为50Hz;
(2)阻抗;
(3)串联电容器;
(4)并联电抗器。
2 数学模型的建立
以上述自动控制元件为根据,可以建立该系统的数学模型,具体分为以下几个步骤:
(1)确定数学模型各环节模块[2]。即新建Simulink的模型窗口,按照系统元件和给定的输入信号、传递函数等,将全部组件拖入界面中。
(2)联接系统的相邻模块。利用系统各个部件之间的信号传递先后顺序,用“→”连接相邻模块,直至组合成系统整体。
(3)设置系统参数。各个环节确定后,通过计算微分方程,确定每个模块的传递函数、空间状态函数等。然后,将函数经过拉式变换,获得的方程式各项增益,就是各模块需要设置的参数。
由于系统运行时,外界存在扰动因素。因此,为确保控制精度,系统采取的结构为闭环结构。电力拖动系统的数学模型,如图1所示。
3 系统动态性能仿真
对于系统的动态性能仿真中,选取最不利条件进行计算,可以获得系统最严峻的动态性能,若该性能满足要求,则其余条件下,系统性能亦满足要求。所以,控制系统的输入信号确定为单位阶跃输入。
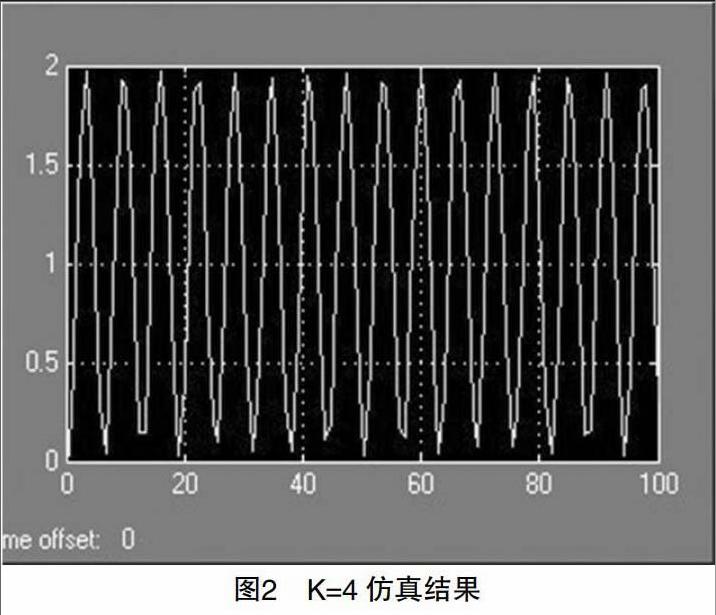
由于通过微分方程、状态空间函数的计算,系统大部分的增益值已是定值,故不存在调节的可能性。此外,系统由于并不存在缺项等问题,故也未选择PI控制器来调整性能。由图1可知,确定系统性能的可调参数,仅有K值。首先,根据经验,取一个较大的K值进行计算[3]:K=4。该参数下的仿真结果,如图2所示。
图2 K=4仿真结果
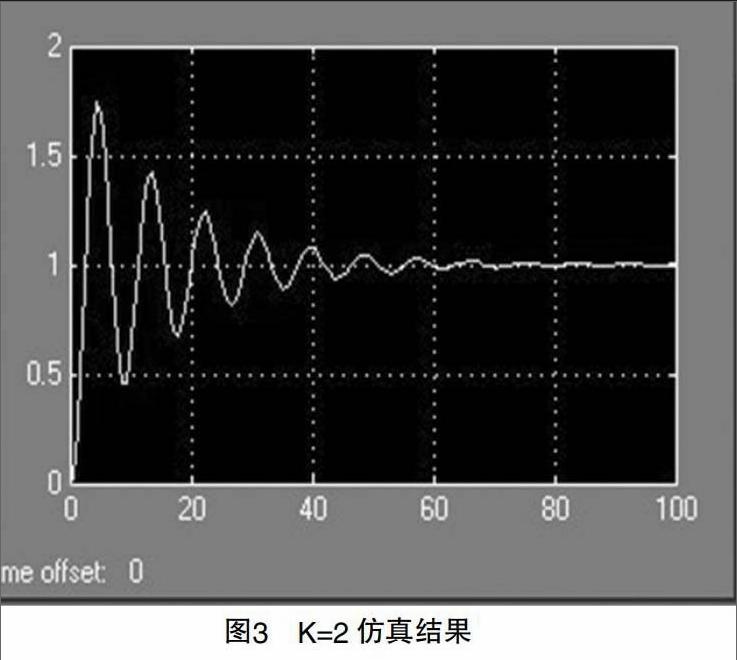
如图2所示,系统在阶跃信号的作用下,自开启之后,处于等幅振荡状态。然而,判断系统能否实现稳定,是以波形是否衰减为依据,当波形逐渐衰减,系统则越发趋于稳定值,以此达到稳定运行状态。所以,从图2所示的波形来看,系统并未实现稳定,即动态性能不佳。因此,必须进一步调整K值。理论上来说,K值取得越小,系统的收敛性越强。因此,取系数K为:K=2。仿真结果,如图3所示。
由图3可知:
(1)该系统的动态性能,从初始到60s,曲线振荡频率减弱,幅值降低。40s后,基本进入稳定运行阶段,即系统是稳定的。
(2)虽然系统是稳定的,但动态性能的指标如何,决定系统的运行寿命。从指标的数据来看,调整时间,约为40s;最大超调量约23%,完全符合国家定义的标准[3]:2.5%~25%。由此可知,该系统的动态性能指标良好。
综上所述,当系统的K值取为2时,系统能够实现收敛的目标,动态性能参数也全标准范围内。由此可以得出结论:该系统的动态特性较好,控制精度较高。
4 结论
本文在对某电力拖动系统的稳定性数值计算中,通过分析系统的组成结构,选择了闭环控制的方式。根据传递函数和微分方程,建立了系统的数学模型。在仿真过程中,选取两组K值进行计算结果比较。结果显示,当K=2时,系统的动态性能较为优越,即达到了优化设计的目的。
【参考文献】
[1]李梅兰,卢文鹏.电力系统分析[M].北京:中国电力出版社,2010.
[2]余成波,张莲,胡晓倩.自动控制原理[M].北京:清华大学出版社,2009.
[3]蒋珉,柴干,王宏华,等.控制系统计算机仿真[M].北京:电子工业出版社,2012.
[4]王旭,李萍,等.水轮机椭圆蜗壳设计的CFD计算及试验分析[J].人民黄河,2016,38(1):109-111.
[5]孙浩,李艳,等.基于Matlab/Simulink的电力系统故障仿真与分析[J].硅谷,2012(22):23-24.
[6]余洋.基于Simulink的电力系统稳定器(PSS)应用仿真[J].科技风,2012(9):62-63.

