Investigation of cavitation bubble collapse near rigid boundary by lattice Boltzmann method*
Ming-lei SHAN (单鸣雷), Chang-ping ZHU (朱昌平), Xi ZHOU (周曦), Cheng YIN (殷澄),
Qing-bang HAN (韩庆邦)
College of Internet of Things Engineering and Jiangsu Key Laboratory of Power Transmission and Distribution
Equipment Technology, Hohai University, Changzhou 213022, China, E-mail: shanming2003@126.com
Investigation of cavitation bubble collapse near rigid boundary by lattice Boltzmann method*
Ming-lei SHAN (单鸣雷), Chang-ping ZHU (朱昌平), Xi ZHOU (周曦), Cheng YIN (殷澄),
Qing-bang HAN (韩庆邦)
College of Internet of Things Engineering and Jiangsu Key Laboratory of Power Transmission and Distribution
Equipment Technology, Hohai University, Changzhou 213022, China, E-mail: shanming2003@126.com
The dynamics of the bubble collapse near a rigid boundary is a fundamental issue for the bubble collapse application and prevention. In this paper, the bubble collapse is modeled by adopting the lattice Boltzmann method (LBM) and is verified, and then the dynamic characteristics of the collapsing bubble with the second collapse is investigated. The widely used Shan-Chen model in the LBM multiphase community is modified by coupling with the Carnahan-Starling equation of state (C-S EOS) and the exact difference method (EDM) for the forcing term treatment. The simulation results of the bubble profile evolution by the LBM are in excellent agreements with the theoretical and experimental results. From the two-dimensional pressure field evolution, the dynamic characteristics of the different parts during the bubble collapse stage are studied. The role of the second collapse in the rigid boundary damage is discussed, and the impeding effect between two collapses is demonstrated.
cavitation mechanics, lattice Boltzmann method, bubble collapse, rigid boundary
Introduction
The bubble collapse near a rigid boundary may lead to a serious material damage owing to the resulted high velocities, pressures, temperature, but on the other hand, it could also be utilized in various important applications, such as for environmental protection,high-intensity ultrasonic therapy and material surface cleaning[1]. However, as too many phenomena are involved, a theoretical model is difficult to establish,and under particular boundary conditions, the analytical solution is usually impossible. Therefore, the numerical simulation becomes a powerful way to gain an understanding. The conventional numerical simulation methods for the non-spherical cavitation bubble mainly include the finite volume method (FVM), the finite element method (FEM) and the boundary element method (BEM)[2]. In the numerical simulations based on the classical partial differential equation, the methods to track or capture the interfaces are required(such as the volume of fluid (VOF) method or the level set method (LSM)[3]). In addition, the Poisson equation needs to be solved to satisfy the continuity equation, which drastically reduces the computational efficiency[4].
During the past decades the lattice Boltzmann method (LBM) has emerged as a powerful tool for simulating multiphase flow problems[4-7]. As a powerful tool for the numerical simulations and investigations of the multiphase flows, the LBM has many advantages, including clear physical pictures, easy implementation of boundary conditions, and fully parallel algorithms[4]. Particularly, it is not required to track or capture the interfaces in the LBM models due to their mesoscopic nature. The Shan-Chen model,which is widely used in the LBM multiphase community due to its simplicity, high computational efficiency and high flexibility, has been introduced into the field of the bubble cavitation recently. The first attempt to validate the application of the Shan-Chen model in the LBM for cavitation problems was made bySukop and Or[8]. Chen et al.[9]simulated the cavitating bubble growth using a modified Shan-Chen model with a large density ratio in both quiescent and shear flows, and the results were compared with the Rayleigh-Plesset equation. The acoustic cavitation of the spherical bubble was simulated recently by Zhou et al.[10]using the original Shan-Chen pseudopotential model, and the result was compared with the Keller equation. Mishra et al.[11]introduced a model of cavitation based on the Shan-Chen multiphase model that allows for coupling between the hydrodynamics of a collapsing cavity and the supported solute chemical species. However, the pressure field evolution in the bubble collapse stage near a rigid boundary has not been extensively investigated yet, in particular, when multiple collapses exist. In addition, due to the inherent parallelism, the LBM promises to be a powerful tool for the studies of the multi-bubbles collapse and even the cavitation field.
The evolutions of the bubble profile and the jet velocity were investigated by experiments with respect to the dynamics of the bubble collapse near rigid boundary[12-14]. As an intuitive clue to investigate the mechanism of the collapsing bubble, the pressure field evolution and the damage of the rigid boundary are more complex and diverse when multiple collapses exist. However, the direct measurement by the experimental method is difficult because all the intrusive measurements will disturb the original pressure field,and the non-intrusive methods cannot be applied unless the fluctuation of the pressure is large enough. In order to visualize the impulsive high pressure regions around the collapsing bubbles, Philipp[12]used the shadow graph method in a high-speed photograph. But the details of the pressure field cannot be obtained except by the emitted shock waves. In Ref.[15], the velocity field and the pressure distribution around the bubble in the dielectric fluid were studied numerically. By solving the Navier-Stokes equation, Liu[16]simulated the pressure distribution numerically outside a nonlinear resonance bubble in one dimension. However, the 2-D pressure distribution and the evolution of a collapsing bubble throughout the whole collapsing stage were not obtained. Since the pressure distribution can be directly obtained by solving the equation of state (EOS), the LBM is very effective to simulate the 2-D or 3-D pressure field and the evolution of a collapsing bubble near a rigid boundary.
In the present work, an approach of bubble collapse simulation is developed based on a modified Shan-Chen model to investigate the bubble collapse near a rigid boundary, especially to investigate the 2-D pressure filed evolution around a collapsing bubble associated with twice collapses. The modified Shan-Chen model is coupled with the Carnahan-Starling equation of state (C-S EOS) and the exact difference method (EDM) in the interaction forcing term treatment, to obtain a large density ratio liquidvapor system while reducing the spurious currents and minimizing the thermodynamics inconsistency. In this work, the simulations by the LBM is verified through a comparison between the simulation results of the bubble profile evolution and the experimental results. Subsequently, the 2-D pressure field evolution around the collapsing bubble associated with twice collapses is investigated, and the role of the second collapse in the rigid boundary damage is discussed.
1. Numerical model
The LBM is a mesoscopic numerical simulation method based on statistical physics and can well simulate the Navier-Stokes equations at the macroscopic scale[4-6]. In the LBM, the motion of fluid is described by a set of particle distribution functions. The standard LBM with a force term based on Bhatnagar-Gross-Krook (BGK) collision term, called the LBGK, can be expressed as follows


The equilibrium distribution function satisfying the Maxwell distribution in the D2Q9 model is expressed as


Based on the aforementioned LBGK model, the inter-particle interaction force is introduced into the Shan-Chen model to simulate the single component multiphase flows[17]. In the D2Q9 model, the nearest neighbor interactions are expressed as


With this method, various EOS can be substituted into Eq.(6). For the C-S EOS, which modifies the vdW EOS, we can obtain
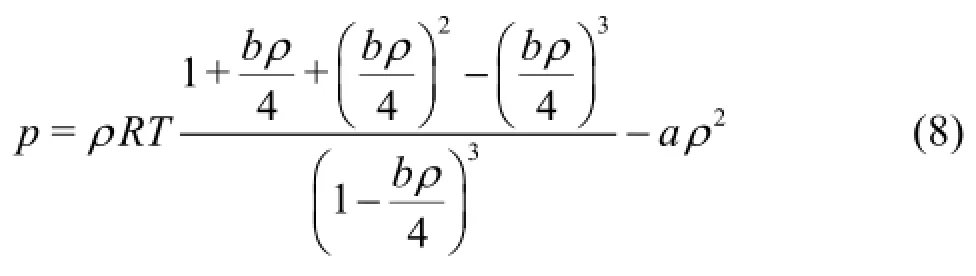
It is shown that the EDM leads to the relaxation time independence and a relatively wide temperature range[19]. In the EDM[20], the force term in Eq.(1) can be expressed as

Fig.1 Computational domain
2. Results and discussions
The simulations of the bubble collapse stage near a rigid boundary are divided into two main parts. In the first part, the simulations are verified by comparing with the classic results of numerical calculations and experiments. In the second part, the pressure field evolution around a collapsing bubble is obtained in detail. In both parts, the computational domain is set as 401×401 for the bubble collapse simulation as shown in Fig.1, whereis the initial radius of bubble,is the distance from the bubble center to the rigid boundary,is thevapor pressure in bubble,is the ambient pressure. In the simulation, with the reduced temperature in the CS-EOS ,the equilibrium pressureis obtained. The pressure boundary conditions are applied in the inlet,and the initial value of the pressure is equal to the equilibrium pressure. Corresponding to the experiments in Refs.[12] and [13], an infinite medium area needs to be established in the computational domain. On account of both symmetrical and asymmetrical situations, a non-equilibrium extrapolation scheme[22]of the boundary condition is applied on both left and right sides to make an infinite area regardless of reflected waves. The bottom boundary is set as a plane rigid boundary with a bounce-back boundary condition. Under the assumptions set by Plesset and Chapman[23], the simulation can be characterized by the stand-off parameterand the constant pressure differencebetween the ambient liquid and the bubble vapor. Unless otherwise specified, the unit adopted in this paper is the lattice unit of the LBM, and the lattice spacing and the time step are equal to unity in this work.

Fig.2 Comparison of bubble profile evolution between the LBM and the experimental results[12]
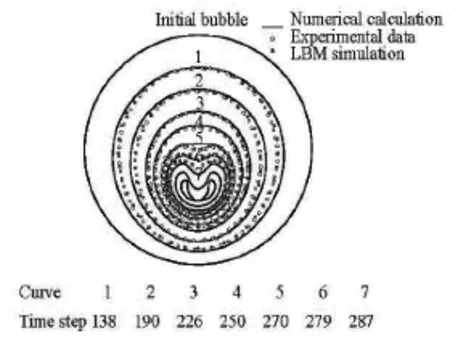
Fig.3 Comparison of bubble surfaces evolution between the simulation of LBM () and the experimental results[13]and calculations[23]
2.1 Bubble profile evolution
With the modified Shan-Chen model, a large density ratio liquid-vapor system can be obtained with different temperatures and different relaxation timesThe coexisting densities of vapor and liquid,and, are determined by the phase segregation simulation with slight random perturbations in the initial density.can be varied slightly in the simulation to obtain an additional pressure difference between the inside and the outside of the bubble after the equilibrium of the fluid in the whole computational domain.

Fig.4 Pressure field evolution around collapsing bubble near rigid boundary (,R0=80,)
Two bubbles with same initial radii and different stand-off parameters are simulated. From the figures of the density field, the bubble profiles can be distinguished visually. In Fig.2, the bubble profile evolutions during the collapse stage are compared with experimental results of Philipp[12]. In both cases, the bubble profile evolutions are in qualitatively good agreement with the experimental results.
With the time step matching, the time evolution of the bubble surfaces can be obtained. The liquid and vapor interface is defined as the locations with the density. For every obtained interface by post-processing is just one set of discrete points, a cubic interpolation is used to obtain a smooth interface. The results are shown in Fig.3. For the convenience, the generalized initial bubble radius is adopted. The LBM simulation results agree better with experimental results[13]than the numerical calculations[23]. In Ref.[23], Plesset and Chapman computed the time evolution of the bubble collapse stage using the boundary element method from the generalized Bernoulli equation. In the definition of the problem, Plesset and Chapman made six assumptions, such as, negligible surface tension, constant vapor pressure and ambient pressure, incompressible liquid, non-viscous flow, no permanent gas, which are difficult to be satisfied in the experiment and the LBM simulation.
From Fig.2 and Fig.3, we can find that the initially spherical bubble starts to collapse due to the pressure difference between the outside and the inside of the bubble. Owing to the rigid wall, the radial liquid flow is retarded, and a region with lower density/pressure is formed near the rigid wall. Therefore, the collapsing bubble is deformed and the jet is originated from the upper wall to the lower one. It is obvious that different stand-off parametersand/or pressure differencewill lead to different morphologies of collapsing bubbles, which should be investigated. In order to be more intuitive, the pressure field evolution of the collapsing bubble is investigated in the next section.
2.2 Pressure field evolution
The simulated pressure field at typical moments are shown in Fig.4. From 4(a) to 4(c) in Fig.4, the bubble deforms from a spherical bubble to an elonga-ted one in the direction normal to the rigid boundary due to the lower pressure region formed near the rigid boundary. The rebound effect of the liquid and the relatively higher speed motion of the upper portion of the bubble cause the forming of a conical high pressure region just above the bubble, which plays a crucial role in the second deformation part, as shown in 4(d)and 4(e). The first collapse, the formation of a circular bubble and the second collapse are illustrated in 4(f),4(g), 4(h), respectively. After the second collapse, the visible bubble surface disappears completely. The circular negative-pressure region formed after the second collapse, as shown from 4(i) to 4(m), is a non-negligible cause of the next collapse or the high frequency oscillation. The interactions between pressure waves lead to a complex sound field in the liquid domain and twice damages of the rigid boundary (as shown in 4(k)and 4(m)).
Making a comprehensive survey throughout the pressure field evolution, the whole process of evolution can be divided into the following typical parts: the first deformation part, the second deformation part,the first collapse, the circular bubble formation part,the second collapse and the post-collapse part. The collapse mechanism aforementioned can be confirmed by the experiment of Philipp[12], and more details of the post-collapse part are shown in our simulation.
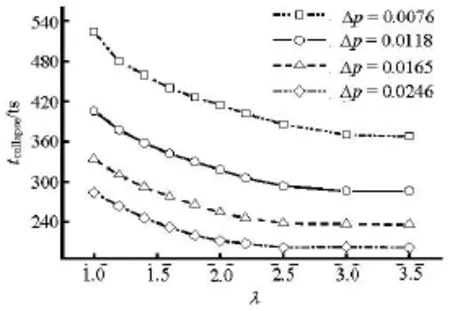
Fig.5 Collapse time
3. Discussions
For a spherical collapsing bubble, the collapse time, i.e., the time duration between the initial stage and the first collapse, can be estimated by the Rayleigh collapse time

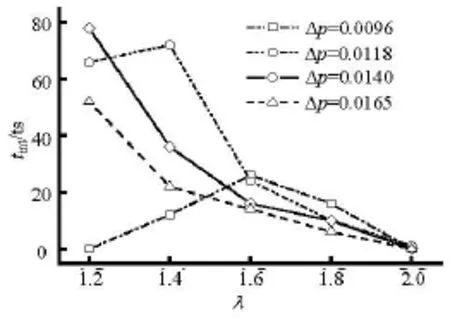
Fig.6 Intervals between first and second collapses
As compared with the pressure field in the case of a single collapse, the pressure field in the case of two collapses is more complex, and the process of the damage of the rigid boundary caused by the collapsing bubble is much varied. In Fig.6, the interval between the first and second collapses,, under variable conditions, is determined for a given. With a highdecreases with the increase of. But for a lower, the interval curve will have an extreme point, which shifts to the right with the decrease of. To better understand this phenomenon, the images of the pressure field evolution corresponding to the case of a lowin Fig.6 are displayed in Fig.7. Essentially,is related with the velocity of the deformation of the collapsing bubble in the second deformation part, and bothandaffect the deformation velocity of the collapsing bubble. Whenis very low, the velocity of collapsing is low. So when the first collapse occurs, a smaller circular bubble is formed (as shown in Fig.7(a)). Due to the low collapsing velocity, the smaller circular bubble can last for a considerable time. However, if theis small enough in this state, the retarding effect of the rigid wall would make the circular bubble further reduce its size, and then shorten the time. For a higherin Fig.7(b), a greater pressure gradient cause a higher deformation velocity of the bubble and then a larger circular bubble, which can last for a longer time. But a very high deformation velocity will, instead, lead to a decrease ofas in the highercases shown in Fig.6. Ifis small enough as shown in Fig.7(b), the pressure wave created by the first collapse and its echo from the rigid wall will accelerate the collapse and then shorten the time

Fig.7 Pressure field at first and second collapses for lowercases in Fig.6

Fig.8 Time sequences ofandon the rigid boundary with different
The crucial role of the pressure and the jet velocity on the wall damage is shown by the comparison in Fig.8 visualizing the time sequences of two parameters,and, which are the pressure and the normal jet velocity against the rigid boundary, respectively. With the decrease of, the distinction between the first collapse and the second one, according toand, is more and more blurred. The maximums ofandvary oppositely to that of the distance between the bubble and the rigid boundary. But, when, both ofandare reduced more than when. Therefore, it can be speculated that there exists an impeding effect between the two collapses at a certain
4. Conclusions
In this paper, the modified Shan-Chen model of the LBM is adopted to simulate the bubble collapse near a rigid boundary. The simulated bubble profile evolution and the bubble surface evolution are in excellent agreements with the theoretical and experimental results. The pressure field evolutions give clear physical pictures for understanding the mechanism of the bubble collapse near a rigid boundary. In particular, the pressure field evolution provides more details after the second collapse. It is shown that the number of parts during the collapse stage and the time intervals among different parts can be adjusted by some parameters, such as.The second collapse makes the pressure field more complex and the process of the damage of the rigid boundary more varied. Additionally, the impeding effect between two collapses at certainis found. It is demonstrated that the LBM is a powerful tool for the study of cavitation under sophisticated boundary conditions and with a large scale cavitation field. Moreover, the investigation of the different parts during the bubble collapse stage and the role of the second collapse provide some insights for the engineering bubble collapse applications or preventions.
Acknowledgments
This work was supported by the Fundamental Research Funds for the Central Universities of Hohai University (Grant No. 2013B08814).
References
[1] FRANC J. P., MICHEL J. M. Fundamentals of cavitation[M]. Dordrecht, The Netherlands: Kluwer Academic Publishers, 2004, 5-6.
[2] LINDS. J., PHILLIPST. N.The effect of viscoelasticity on the dynamics of two gas bubbles near a rigid boundary[J]. IMA Journal of Applied Mathematics, 2012,77(5): 652-677.
[3] SAMIEI E., SHAMS M. and EBRAHIMI R. A novel numerical scheme for the investigation of surface tension effects on growth and collapse stages of cavitation bubbles[J]. European Journal of Mechanics-B/Fluids, 2011, 30(1): 41-50.
[4]SUKOP M. C., THORNE D. T. Lattice Boltzmann modeling: An introduction for geoscientists and engineers[M]. New York, USA: Springer-Verlag, 2006, 1-4.
[5] CHEN L., KANG Q. and MU Y. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications[J]. International Journal of Heat and Mass Transfer, 2014, 76(6): 210-236.
[6] XU Ai-guo, ZHANG Guang-cai and LI Ying-jun et al. Modeling and simulation of nonequilibrium and multiphase complex system-lattice Boltzmann kinetic theory and application[J]. Progress in Physics, 2014, 34(3): 136-167(in Chinese).
[7] DIAO Wei, CHENG Yong-guang and ZHANG Chun-ze et al. Three-dimensional prediction of reservoir water temperature by the lattice Boltzmann method: Validation[J]. Journal of Hydrodynamics, 2015, 27(2): 248-256.
[8] SUKOP M., OR D. Lattice Boltzmann method for homogeneous and heterogeneous cavitation[J].Physical Review E, 2005, 71(4): 046703.
[9] CHEN X. P., ZHONG C. W. and YUAN X. L. Lattice Boltzmann simulation of cavitating bubble growth with large density ratio[J]. Computers and Mathematics with Applications, 2011, 61(12): 3577-3584.
[10] ZHOU X., SHAN M. and ZHU C. et al. Simulation of acoustic cavitation bubble motion by lattice Boltzmann method[C]. 4th International Conference on Civil Engineering, Architecture and Building Materials. Wuhan,China, 2014, 3098-3105.
[11] MISHRA S. K., DEYMIER P. A. and MURALIDHARAN K. et al. Modeling the coupling of reaction kinetics and hydrodynamics in a collapsing cavity[J]. Ultrasonics Sonochemistry, 2010, 17(1): 258-265.
[12] PHILIPP A., LAUTERBORN W. Cavitation erosion by single laser-produced bubbles[J]. Journal of Fluid Mechanics, 1998, 361: 75-116.
[13] LAUTERBORN W., BOLLE H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary[J]. Journal of Fluid Mechanics, 1975,72(2): 391-399.
[14] WANG Q. X., YANG Y. X. and TAN D. S. et al. Nonspherical multi-oscillations of a bubble in a compressible liquid[J]. Journal of Hydrodynamics, 2015, 26(6): 848-855.
[15] SHERVANI-TABAR M. T., MOBADERSANY N. Numerical study of the dielectric liquid around an electrical discharge generated vapor bubble in ultrasonic assisted EDM[J]. Ultrasonics, 2013, 53(5): 943-955.
[16] LIU Hai-jun. Pressure distribution outside a single cavitation bubble[J]. Acta Physica Sinica, 2004, 53(5): 1406- 1412(in Chinese).
[17]SHAN X., CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J].Physical Review E, 1993, 47(3): 1815-1819.
[18] YUAN P., SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18(4): 042101.
[19] LI Q., LUO K. H. and LI X. J. Forcing scheme in pseudopotential lattice Boltzmann model for multiphase flows[J].Physical Review E , 20 12, 8 6(1): 016709.
[20] KUPERSHTOKHA.L.,MEDVEDEVD.A.and KARPOV D. I. On equations of state in a lattice Boltzmann method[J]. Computers and Mathematics with Applications, 2009, 58(5): 965-974.
[21] KLASEBOER E., KHOO B. C. and HUNG K. C. Dynamics of an oscillating bubble near a floating structure[J]. Journal of Fluids and Structures, 2005, 21(4): 395-412.
[22] GUO Zhao-li, ZHENG Chu-guang. Theory and applications of lattice Boltzmann method[M]. Beijing, China: Science Press, 2008, 65-67(in Chinese).
[23] PLESSET M. S., CHAPMAN R. B. Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary[J]. Journal of Fluid Mechanics, 1971, 47: 283-290.
November 11, 2014, Revised January 19, 2015)
* Project supported by the National Natural Science Foundation of China (Grant Nos. 11274092, 11274091 and 1140040119), the Natural Science Foundation of Jiangsu Province (Grant No. SBK2014043338).
Biography: Ming-lei SHAN (1977-), Male,
Ph. D. Candidate, Lecturer
- 水动力学研究与进展 B辑的其它文章
- Scattering of gravity waves by a porous rectangular barrier on a seabed*
- Numerical simulations of viscous flow around the obliquely towed KVLCC2M model in deep and shallow water*
- A simple method for estimating bed shear stress in smooth and vegetated compound channels*
- Theoretical analysis and numerical simulation of mechanical energy loss and wall resistance of steady open channel flow*
- A robust WENO scheme for nonlinear waves in a moving reference frame*
- Oscillating-grid turbulence at large strokes: Revisiting the equation of Hopfinger and Toly*

