基于VSP地震资料的品质因子提取方法

董　博，纪春玲，周安聘，李　凤，张环曦，赵雨晨，刘　静，牛淑瑜

(1.河北地质大学，石家庄　050031；2.河北省地震局石家庄中心台，石家庄　050021)



基于VSP地震资料的品质因子提取方法

董博1，2，纪春玲1，周安聘1，李凤1，张环曦1，赵雨晨1，刘静1，牛淑瑜1

(1.河北地质大学，石家庄050031；2.河北省地震局石家庄中心台，石家庄050021)

介绍了改进的频谱比方法原理、影响因素及其优点，并利用改进的谱比法对胜利油田某工区采集到的VSP地震资料进行测试，对所有下行反射波进行振幅谱计算。结果显示，该方法使得提取出来的品质因子Q值计算精度得到了提高，计算结果更加真实可靠。

品质因子；改进的谱比法；吸收衰减；傅里叶变换；影响因素

0　引言

品质因子Q能够量化为介质的粘弹性所导致的地震波传播过程中能量的衰减和频散，它是用来表征岩层吸收衰减特征的参数[1]。弹性介质中传播的地震波没有能量的衰减，因为介质的Q值趋于无穷大。介质的粘弹性和Q值呈反比例关系，随着Q值的增大,介质的粘弹性减小，介质的吸收衰减作用也就越小，反之亦成立[2]。地下介质对地震波的吸收衰减作用包括岩层的非固有衰减和固有衰减[2]。在计算地层的固有衰减时，应该首先消除几何扩散、非弹性以外的散射、与频率有关的透射和反射等非固有衰减因素的影响。因为无法完全地分离并消除这些因素，在计算等效Q值时还是会受到这些因素的影响[3]。

1　常用品质因子的计算方法

根据计算方法原理的不同，可以把传统品质因子Q的计算方法分为时间域和频率域方法。因为每种计算方法的适用条件和对地震资料信噪比的要求不一样[2]，所有方法均不具有普遍适用性。

时间域中计算品质因子Q的方法主要包括：相位模拟法、上升时间法、脉冲振幅法、解析信号法、子波模拟法、瞬时频率模拟法和振幅衰减法等。时间域求取Q值的方法所面临的困难是地震资料的信噪比较低，振幅信息不保真，还不能通过有效的技术方法进行准确校正，因而时间域方法计算精度不高，在实际资料的处理中应用很少。

频率域计算品质因子Q的方法主要有：频谱比法、谱模拟法、质心频率偏移法、匹配拟合技术等。但是每种方法的适用条件和计算精度都不太一样。例如谱模拟方法[4-5]，是Rosa等人提出在地震子波振幅谱的基础上进行计算的[6]，主要是考虑了振幅的变化，而没有考虑相位的变化。频谱比法同时考虑了相位变化和振幅变化。

频谱比法在计算中涉及到的振幅谱必须是在目的层的上层位和下层位中分别选取得到的，然后利用选取的地震子波记录段进行频谱分析和Q值的计算。假设地震波在t1和t2处的振幅谱分别为[7]：

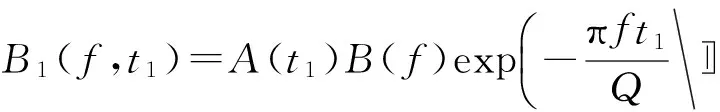
(1)

(2)

式中:A(t)是与频率无关的函数，代表其它因素对地震波衰减的影响。B(f)是初始时刻地震子波的振幅谱。观察可以发现，谱比法中频谱比的斜率是Q的函数，对频谱比等式两边取对数得：

(3)

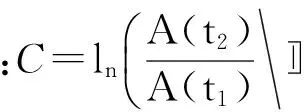
(4)

由式(4)可以计算出地层等效Q值[8]。目的层厚度随时间间隔的增大而变大，谱比法的计算结果也逐渐趋近于一个常数。如果排除了非固有衰减对Q值估计的影响，那么等效Q值只与地层介质的吸收性质有关。

2　改进的频谱比法基本原理

零偏移距VSP资料可以为估计品质因子值提供很好的数据,我们利用近偏移距VSP资料估计品质因子值。改进的谱比法是利用所有的下行反射波而不是只利用直达波进行计算[9]。首先，我们利用波场分离将下行波场从近偏移距VSP资料中分离出来;然后，在频率域中利用下行波场进行计算。将地震数据从时间域变换到频率域常用的方法是S变换和傅立叶变换。

为了提高Q值的提取精度，需要在频率域进行计算，将地震数据变换到频率域常用的有傅立叶变换和S变换方法，尤其是傅立叶变换。利用傅立叶变换将地震记录变换到频率域，在频率域提取Q值[9]，近偏移距VSP资料Q值估计通常是假设在频率域中吸收是线性相关的(常数Q)，谱比法的表达形式是：

S2(f)=C×S1(f)e-α1,2t1,2f。

(5)

其中，吸收系数与Q的关系为：

Q=π/α1,2,

(6)

对方程(5)取对数：

log(S2(f)/S1(f))=b-α1,2t1,2f 。

(7)

其中：b=log(C)，为了估计吸收系数α，并且避免产生较大的误差，最小化函数G：

(8)

式中:

(9)

将(8)带入(9)可以得到目标函数：

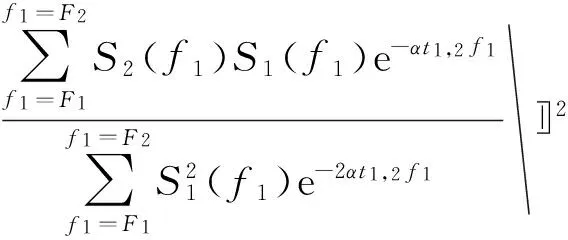
(10)

在给定的α范围内，找出G1(α)的最小值，从而可以得到α值。由于VSP地震数据信噪比较高，利用VSP地震数据进行计算时没有必要再进行道集归一化或者是几何扩散补偿。从公式(5)可以推出zm,zk层振幅之间的关系表达式：

Sm(f)=Const×Sk(f)e-Ak,m(Tm-Tk)f。

(11)

(12)

从方程(11)和(12)可以得到平均速度和层间速度关系以及有效吸收系数与层间吸收系数之间的关系。不同的是，我们知道从地表到最浅层检波器的平均速度，而不知道从地表到最浅层检波器的吸收系数，有效吸收系数和平均速度的表达式如下：

(13)

在方程式(13)中，只保存那些在给定范围之内的Ak,m。如果所有的Qk,m都在合理的范围内，则应该有N(N-1)/2个值。通常情况下，大概有总数的1/4，这为稳定的Q值估计提供了良好的统计条件。

3　实际资料处理

为保证结果的可靠性，本文3.1和3.2节所选用数据均来自于胜利油田某工区周边的VSP炮记录，与3.3节所用VSP炮记录场地相邻，数据共100道，采样间隔为1 ms，资料处理模型选用层状衰减—频率曲线的粘弹性VSP地震响应模型。

3.1改进的谱比方法的影响因素

地下介质中地震波能量的衰减受到很多因素的影响，其中有些因素与地震波的频率无关，例如反射透射损失、波前发散等。除了地层吸收作用的影响以外，其它因素在地震波的频率发生变化时对地震波的能量产生的影响很小。从地震波衰减机理上讲，采用谱分析方法估算地层的吸收衰减性质是可行的[7]。

谱比法是计算品质因子Q值的最常用方法，而改进的谱比法虽然VSP地震记录的信噪比较高，可以计算出较精确的品质因子Q值，但是仍然受到如时窗的长度、形状等诸多因素的影响。

层状衰减—频率曲线的粘弹性VSP地震响应模型分3层(图1)，第1层Q值为200，第2层的Q值为30，第3层的Q值为40。上行反射波能量相对于下行反射波能量小的多，因为下行波能量太强，导致上行反射波不清楚。在这里估算品质因子Q时，采用下行波(图2)。在求取Q的过程中，以第1层的Q值计算为例，分析时窗长度、类型、噪声等各种因素对Q值计算结果的影响。因为每2道数据就可以计算出一个Q值，为了减少不必要的误差，在分析结果时利用等效品质因子值进行比较。从计算结果(图3～11)可以看出，在近道和远道存在误差。近道误差主要是因为受到震源的影响，远道误差是因为接近强吸收层，在2层分界面附近计算结果会受到一些影响。

图1　粘弹性VSP地震响应

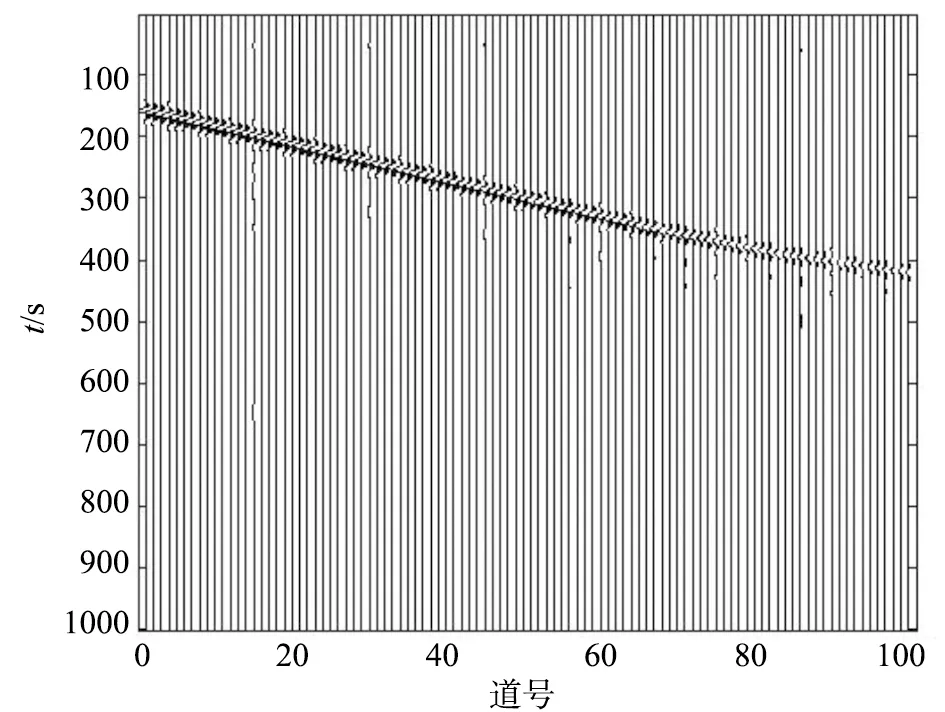
图2　下行波地震响应

3.1.1时窗长度的影响

等效品质因子值为计算品质因子值的平均值。对比图3和图4，时窗长度为128 ms的等效品质因子值为214.557 8，时窗长度为256 ms的等效品质因子值为206.390 6。对比结果说明，时窗长度的适当增加，对改进的谱比法结果有一定的改善作用。

注：加矩形时窗，时窗长度128 ms，起止频率为1～90 Hz图3　时窗长度为128 ms的等效Q值

注：加矩形时窗，时窗长度256 ms，起止频率为1～90 Hz图4　时窗长度为256 ms的等效Q值

3.1.2不同时窗函数的影响

通过计算，加矩形窗的等效品质因子值为206.390 6，加汉宁窗的值为226.013 3。对比图4和图5，说明时窗类型的改变对改进的谱比法结果具有一定的影响，在计算时应选择合适的时窗函数。通过对各种窗函数的验证比较，因矩形窗主瓣比较集中，能量相对集中在主瓣，较接近真实的频谱。在本章的计算中我们选择矩形时窗。

注：添加汉宁窗，时窗长度为256 ms，起止频率为1～90 Hz图5　添加汉宁窗后的等效Q值

3.1.3起止频率的影响

计算时起止频率的选择是多次试验总结得出的最佳频率选择范围，图4和图6进行比较说明，计算结果稳定的前提是频率范围的选择要合理。

注：加矩形时窗，时窗长度256 ms，起止频率为1～70 Hz图6　起止频率为1～70 Hz的等效Q值

3.1.4初始Q值的影响

比较图7和图8可以看出，只有选择合理的初始Q值，最终的计算结果才会比较稳定。模型给出的理论Q值为200，该Q值说明地震波的衰减相对较小。当理论模型为一般衰减层而给出的初始Q值为强衰减层时，计算结果不稳定；只有当初始值与理论模型衰减程度相当时,计算结果才比较稳定。

注：时窗长度256 ms，起止频率为1～90 Hz，初始Q=314图7　初始Q=314的等效Q值

注：时窗长度256 ms，起止频率为1～90 Hz，初始Q=31.4图8　初始Q=31.4的等效Q值

3.1.5噪声的影响

图9～10说明改进的谱比法的计算结果随地震资料中噪声成分的增加越来越不稳定，因此，改进的谱比法对地震资料的品质要求比较高。在没有噪声和干扰波干涉的情况下，该方法计算得到的等效品质因子与品质因子的理论值极其接近。当地震记录中的随机噪声较少时，计算出来的Q值还是可靠的；当地震剖面的信噪比较低时，计算结果就会变得很不稳定，甚至还会出现负Q值的情况。这说明改进的谱比法计算结果的准确性在很大程度上依赖于地震资料信噪比的高低，因此，在进行计算品质因子之前,应该对地震资料进行去噪处理。

注：加噪声0.5%，时窗长度为256 ms，起止频率为1～90 Hz图9　加噪声0.5%的等效Q值

注：加噪声5%，时窗长度256 ms，起止频率为1～90 Hz图10　加噪声5%的等效Q值

3.2改进的谱比法的优点

短时傅立叶变换方法因为不能根据频率的变化进行时窗大小的调节，在使用时受到限制。S变换[10]采用的是可变高斯窗函数，有多尺度聚焦性，可以保持频率的绝对相位，其基本变换函数可以不满足容许性条件，并且可以实现地震信号在时间域和频率域的无损转换。但是S变换基本函数的形态是固定不变的，导致其在应用中受到限制，为此学者们将S变换推广到广义S变换。考虑到傅立叶变换的不足和广义S变换的优点，在这里我们将改进的谱比法中的傅立叶变换改为广义S变换。

(14)

其中：k是大于零的常数。

在广义S变换中，可以通过控制k值来提高时间-频率谱(以下简称“时-频谱”)的时间(或频率)分辨率。但是由于k是常数，所以它若提高了频率分辨率，那么一定是以牺牲时间分辨率为代价的，反之亦然。从总体上来说，S变换得到的时-频谱是基于时频分辨率不变的前提；虽然在广义S变换中，调节k值可以得到相应的多个时间频率谱，但当k值固定不变的时候，由广义S变换得到的时-频谱分辨率具有唯一的变化趋势。为了使时频谱能够更好地反映全时段内所有信号的局部频段的细节，我们引入一个和频率有关的可变因子σf，对Gauss窗函数进行改进[12]，那么Gauss窗函数可以修正为：

(15)

(16)

在这里，我们将σf定义为σf(f)=(kf+b)a。

本文使用的改进的广义S变换方法主要是针对非平稳信号时间频率的特征，该方法含有一个可变的因子函数，函数的自变量是频率。使用时窗函数的类型以及其他参数的调节都是灵活多变的，从而可以避免S变换和广义S变换中时频分辨率的变化趋势问题，增强其适应性和针对性[12]。

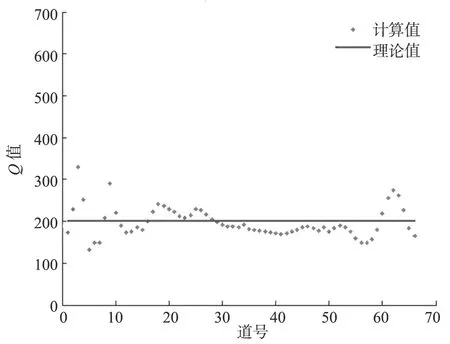
注：广义S变换，起止频率为1～90 Hz 图11　相邻检波器之间的Q值

对比图4中的层Q值206.390 6和图11中的层Q值197.074 9，可以看出，改进的谱比法中利用广义S变换进行时频变换计算得到的地层Q值与理论值误差更小。

利用改进的谱比法对3.1节用的粘弹性VSP地震记录提取品质因子，对波场分离得到的下行波场进行等效品质因子的提取(图12)。提取结果与理论值以及误差见表1。

图12　估计Q值与理论Q值的比较

层数123理论Q值2003040基于广义S变换改进的谱比法201.826230.902640.9690基于傅立叶变换改进的谱比法207.616025.307948.1033基于广义S变换的计算误差0.9%3.0%2.4%基于傅里叶变换的计算误差3.8%15.6%20.3%

通过表1和图12可以看出，基于广义S变换的改进的谱比法提取的Q值与理论Q值匹配效果较好，而基于傅立叶变换的改进的谱比法提取的Q值相对较差。不过总体而言，对于低品质因子的层估计的Q值误差较大，品质因子较大的层估算的Q值误差相对较小，主要原因为Q值小的地层吸收大，Q值较大的地层吸收小。

基于上述结论，在下面的实例中，采用基于广义S变换的改进的谱比法进行品质因子的估算。

3.3改进谱比法的应用实例

选用胜利油田某工区采集到的VSP炮记录进行测试。具体采集参数为：采用零井源距接收观测系统，震源的沉放深度为15 m，接收道数为315道，道间距为5 m，第一个检波点位于230 m，采样点为2 000，时间采样间隔为0.5 mm(图13)。由于地震资料在采集中受到很多因素的影响，例如多次波和自由噪声等，对该炮记录进行波场分离，得到上行波场和下行场(图14)。为了提取更加准确的等效品质因子，首先对下行波场进行去除噪声处理，采用改进的谱比法进行提取(图15)。由图15看出，该资料存在强吸收层和弱吸收层。在接近地表部位为强吸收层，这与我们常识认知是相符的，因此该计算结果具有一定的可靠性。

图13　VSP炮记录

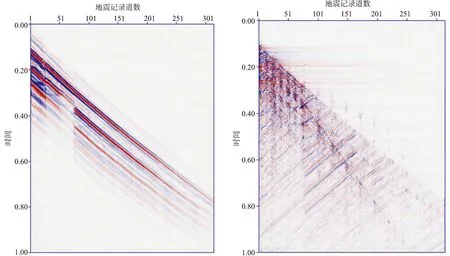
a 下行波场b 上行波场图14　分离得到的波场

图15　提取的品质因子

上述实例表明，利用改进的谱比法对VSP地震资料进行研究，提取出的品质因子计算精度得到了提高。谱比法只是利用VSP资料的直达波进行计算，改进的谱比法利用所有下行反射波进行计算振幅谱，利用改进的谱比法进行计算的结果更加真实可靠。

4　讨论与结论

针对振幅衰减法和解析信号法在计算时需要真振幅数据，而在实际采集中，真振幅数据很难获得,以及谱比法计算时目的层的厚度随时间间隔的增大而变大，计算结果也逐渐趋近于一个常数的问题，利用改进的谱比法求取介质Q值，更符合实际需要。

根据理论分析和实际VSP地震记录数据计算表明：

1)改进的谱比法充分考虑了地层对地震波的吸收作用，使得求得的Q值更符合实际情况。

2)改进的谱比法中利用广义的S变换求取Q值，使得得到的Q值的物理意义更加清晰。

3)采用改进的谱比法求取品质因子时，综合考虑了算法的一些影响因素，对算法进行了相应的改进，使得高频段的分辨率得到了提高，Q值的计算精度也相应提高。

当然Q值计算精度的提高不只是依赖于算法本身的计算精度和地震资料的高信噪比，在实际资料处理时，应该对具体问题进行具体分析。

[1]刘祖沅. 岩石中地震波衰减的实验研究[J]. 地震科学研究. 1983, 6:34-40.

[2]Rainer Tonn. The deternation of the seismic quality factor Q from VSP data:A comparison of different computational methods[J].Geophysical Prospecting, 1991,39(1):1-27.

[3]Aki k,Richards P G. Quantitative Seismology: Theory and Methods[M]. San Francisco: W H Freeman and Company,1980.

[4]王慧茹. 谱模拟频谱比法反演介质品质因子稳定性分析[J]. 物探与化探,2009, 33(1):85-87.

[5]孙成禹. 谱模拟方法及其在提高地震资料分辨率中的应用[J]. 石油地球物理勘探, 2000, 35(1):27-35.

[6]Ricker N H. Transient waves in visco-elastic media [M]. New York: Elsevier Science Publishing Company,1977.

[7]宫同举, 孙成禹, 彭洪超,等. 几种提取品质因子方法的对比分析[J]. 勘探地球物理进展, 2009, 32(4):252-257.

[8]吴琳. 品质因子求取与补偿方法研究[D]. 山东:中国石油大学(华东),2011.

[9]Blias F. Q-factor estimation through optimization approach to near-offset VSP data[J]. SEG Technical Program Expanded Abstracts , 2011:4278-4282.

[10]Stockwell R G,Mansinha L, Lowe R P．Localization of the complex spectrum：The S transform[J]．IEEE transactions on Signal Process,1996,44(4):998-1001.

[11]Mansinha L, Stockwell R G. Local S-spectrum analysis of 1-D and 2-D data[J]. Physics of the Earth and Plantetary Interiors, 1997, 103(3):329-336.

[12]周竹生, 陈友良. 含可变因子的广义S变换及其时频滤波[J]. 煤田地质与勘探, 2011, 39(6):63-67.

Extraction Method of Quality Factor based on VSP Seismic Data

DONG Bo1,2, JI Chun-ling1, ZHOU An-pin1, LI Feng1,ZHANG Huan-xi1, ZHAO Yu-chen1, LIU Jing1, NIU Shu-yu1

(1. Hebei GEO University, Shijiazhuang 050031,China;2. Shijiazhuang Central Seismic Station, Earthquake Administration of Hebei province, Shijiazhuang 050021,China)

This paper studies VSP data in shengli oilfield with advanced spectral ratio method to improve the calculation accuracy of quality factors. Different from traditional spectral ratio method in which only direct waves from VSP data are used to calculate, the advanced one takes all downgoing reflected waves to calculate amplitude spectrum, whose results will be more authentic and reliable.

quality factor; improved spectral ratio method; attenuation; Fourier transform; influencing factors

2016-02-16

2015年度震情跟踪定向工作任务“利用背景噪声监测波速变化系统初步研究”(2015010117)

董博(1986—)，男，河北鹿泉人，助理工程师，现主要从事地震监测与分析预报工作.E-mail：dongbo0002@126.com

P315.6

A

1003-1375(2016)03-0061-07

10.3969/j.issn.1003-1375.2016.03.011

董博，纪春玲，周安聘，等．基于VSP地震资料的品质因子提取方法[J]．华北地震科学，2016，34(3):61-67.