Delta结构3D打印机运动学研究

郑　晓， 王　君

(湖北工业大学机械工程学院， 湖北 武汉 430068)



Delta结构3D打印机运动学研究

郑晓， 王君

(湖北工业大学机械工程学院， 湖北 武汉 430068)

描述一种直线型Delta结构3D打印机的结构，对结构进行了一定等效简化。以该3D打印机机械本体为研究对象，对其运动学反解以及速度反解进行分析与研究，推导出运动学反解方程以及速度反解公式。

3D打印机; 运动学; Delta结构

3D打印(Three Dimension Printing，3DP)技术[1]是采用离散材料(液体、粉末、丝、板、片、块等)逐层累加原理制造实体零件的技术。相对于传统的材料去除技术，3D打印是一种自下而上材料累加的制造工艺[2-3]。进入21世纪以来，Delta系列机器人呈现出高速、高精度、灵活性等发展方向[4]，Pierrot团队相继发明了四支链的H4、I4、Heli4以及Part4等机构[5-7]，Clavel先后提出将外转动副改为移动副的三种变异形式[8]，即直线型Delta结构，本文研究的3D打印机，其结构即为一种直线型Delta结构。

Delta结构3D打印机是Delta结构并联机器人与3D打印的融合。3D打印技术在国内的应用还不十分广泛，因而对3D打印机的研究还处于初期阶段。而目前对Delta结构并联机器人运动学研究主要集中在对四支链机构的研究上，Pierrot[6]、Choi[9]等均采用牛顿迭代法对H4变异机构进行运动学分解求解。对于直线型Delta结构虽有一些研究[10-13]，但其运动学求解方式普遍较为繁琐。针对以上情况，本文对直线型Delta结构3D打印机进行运动学分析，结合几何和代数的方法，求出运动学反解，并在运动学分析的基础上对其进行速度分析，求出其雅克比(Jacobi)矩阵，同时得到其速度反解。该方法相对于传统方法计算更加简单，推导过程更加直观易懂。

1　打印机结构描述

该3D打印机由定平台、动平台以及连接两平台的3个分支组成(图1)，3个分支以定平台中心呈对称分布，具有相同的运动链，都含有一个平面平行四边形机构。该平行四边形机构一端与滑块连接，另一端与动平台连接，动平台中心与该3D打印机的打印头部分相连接，该平行四边形机构可等效为过其上下边中点的一根单杆。滑块安装在直线导轨上，导轨的下方安装有3台步进电机，步进电机带动轴上的同步带轮做旋转运动，同步带轮依靠与滑块固定在一起的同步带，将同步带轮的旋转运动转变为滑块的直线运动，滑块的上下运动使得动平台完成对打印头位置的控制。

图 1　3D打印机实物图

该3D打印机机构简图如图2所示，定平台为一个正三角形△A1A2A3，其特征参数是R；直线导轨垂直于定平台，滑块(移动副)Mi(i=1,2,3)安装在直线导轨上，其位移为li(i=1,2,3)；动平台为正三角形△B1B2B3，其特征参数是r，动平台与移动副通过简化平行四边形机构后的单杆连接，三根单杆杆长均为l。

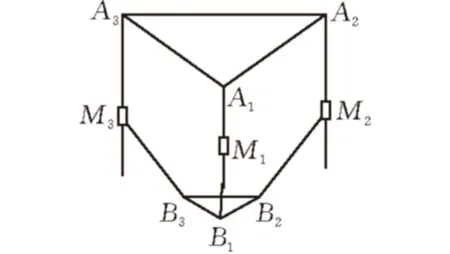
图 2　3D打印机机构简图

2　打印机运动学反解分析

求解运动学反解就是在已知动平台位姿的条件下求解定平台三个移动副的位移量。以定平台几何中心O为坐标原点建立坐标系O-XYZ，以动平台几何中心O′为坐标原点建立坐标系O′-X′Y′Z′，3根单杆即为该打印机机构的3条支链。支链分布见图3，单个支链在XOZ面的投影见图4。

图 3　支链分布图

如图3所示，点Ai为移动副在定系O-XYZ面的投影位置，向量

(1)

其中，αi(i=1,2,3)为OAi与O-XYZ中X轴正向的夹角。

图 4　支链结构简图

沿移动副轴线方向的向量

(2)

则向量

OMi=OAi+AiMi=

(3)

Bi点在坐标系O′-X′Y′Z′中表示为

(4)

(5)

由于三根单杆的杆长是固定的，即向量MiBi的模为l，用等式表示为：

(6)

将式(3)、式(5)代入式(6)中，得到关于移动副位移li的方程

(7)

解方程(7)得

li=Z±

(i=1,2,3)

(8)

根据delta结构3D打印机的设计要求，定平台在动平台上方，根据坐标系的建立可知li>Z，则li最终表达式为

li=Z+

(i=1,2,3)

(9)

上式即为该3D打印机的运动学反解方程。

3　打印机速度反解分析

该Delta结构3D打印机的速度方程可以通过式(7)对时间求导来得到。

将式(7)写成如下形式

(10)

将式(10)两端同时对时间求导，v1、v2、v3表示输入速度(移动副速度)，vx、vy、vz表示输出速度(动平台末端执行器在坐标系O-XYZ内的速度)，整理得

(11)

将式(11)整理成矩阵形式，得

(12)

(13)

J=B-1A,

式(13)反映了输入速度与输出速度之间的关系，J称为此打印机的雅克比(Jacobi)矩阵，同时得到速度反解的公式为

4　结论

1)对于本文介绍的一种直线型Delta结构3D打印机，对其结构进行了详细描述，以杆长作为约束条件，结合代数和几何方法推导出了运动学反解方程。此方法计算过程简单、推导直观。

2)在运动学反解的基础上进一步推导出雅克比(Jacobi)矩阵以及速度反解公式，雅克比矩阵表示了该Delta结构3D打印机输入速度与输出速度之间的关系，是进行动力学分析以及奇异性分析的基础。

[1]科技智囊专题研究小组．3D打印，让世界更精彩[J]．科技智囊，2013(3)：13-17．

[2]中国机械工程学会．3D打印，打印未来[M]．北京：中国科学技术出版社，2013：1-4．

[3]邢鸿飞，保罗·麦基里．第三次工业革命[J]．世界科学，2012(7)：10-11．

[4]冯李航、张为公．Delta系列并联机器人研究进展与现状[J]．机器人，2014(5)：375-382．

[5]PierrotF，NabatV，CompanyO，etal．Optimaldesignofa4-DOFparallelmanipulator：Fromacademiatoindustry[J]．IEEETransactionsonRobotics，2009，25(2)：213-224．

[6]PierrotF，MarquetF，GilT，H4parallelrobot：Modeling，designandpreliminaryexperiments[C]//IEEEInternationalConferenceonRoboticsandAutomation．Piscataway，USA：IEEE，2001：3256-3261．

[7]NabatV，delaRodriguezM，CompanyO，etal．.Par4：Veryhighspeedparallelrobotforpick-and-place[C]//IEEEInternationalConferenceonIntelligentRobotsandSystems．Piscataway，USA：IEEE，2005:553-558．

[8]ReyL，ClavelR．TheDeltaparallelrobot[M]．ParallelKinematicMachines．London，UK：Springer，1999：401-417．

[9]ChoiHB，KonnoA，UchiyamaM．Design，implementationandperformanceevaluationofa4-DOFparallelrobot[J]．Robotica，2010，28(1)：107-118．

[10] 赵杰，朱延河．Delta型并联机器人运动学正解几何解法[J]．哈尔滨工业大学学报，2003，35(1)：25-27．

[11]RomdhaneL．Designandanalysisofahybridserial-parallelmanipulator[J]．MechanismandMachineTheory，1999，34(7)：1037-1055．

[12]XuQS，LiYM．A3-PRSparallelmanipulatorcontrolbasedonneuralnetwork[C]//4thInternationalSymposiumonNeuralNetworks．Berlin：Springer，2007：757-766．

[13]PislaD，PislaA．Therelationshipbetweentheshapeoftheworkspaceandgeometricaldimensionsofparallelmanipulators[J]．ProceedingsinAppliedMathematicsandMechanics，2004，4(1)：67-168．

[责任编校： 张众]

Research on Kinematics of Delta Structure 3D Printer

ZHENG Xiao, WANG Jun

(SchoolofMechanicalEngineering,HubeiUniversityofTechnology,Wuhan430068,China)

This paper studies the kinematic characteristics of a linear Delta structure 3D printer. The printer is composed of a fixed platform, a movable platform and three branches, and the mechanical body is a linear Delta structure. The structure of the 3D printer is described and simplified to some extent. With the 3D printer as the research object, this paper analyzes the kinematics reverse solution and inverse velocity of the 3D printer, based on which the inverse kinematics equation and inverse velocity formula are derived. It provides a theoretical basis for the application of linear Delta structure 3D printer in practical work．

3D printer; kinematics; delta structure

2016-03-22

国家自然科学基金(51405140)； 湖北省自然科学基金重点项目(2015CFA112)； 湖北省教育厅优秀中青年科技创新团队项目(T201505)

郑晓(1991-)， 女，湖北十堰人，湖北工业大学硕士研究生，研究方向为机构综合与分析，机器人学

1003-4684(2016)04-0021-03

TH12

A