基于矢量约束的随机特征点选取算法

马　旭, 程咏梅, 郝　帅

(1. 西北工业大学自动化学院, 陕西 西安 710129;2. 西安科技大学电气与控制工程学院, 陕西 西安 710054)



基于矢量约束的随机特征点选取算法

马旭1,2, 程咏梅1, 郝帅2

(1. 西北工业大学自动化学院, 陕西 西安 710129;2. 西安科技大学电气与控制工程学院, 陕西 西安 710054)

无人机利用视觉在未知区域自主着降时,提取的特征点具有数量多、随机性强等特点。针对利用随机特征点进行位姿估计精度低、稳定性差的问题,提出一种基于矢量约束的随机特征点选取算法。首先通过分析位姿估计方程可知，特征点地理坐标是影响方程组求解精度的重要因素;然后在引入矢量角均分度、矢量模值均值及矢量模值最大值三项约束指标基础上，制定了一种基于矢量约束的特征点选取策略;最后利用正交迭代算法对所选取的特征点进行位姿估计精度验证。实验结果表明，提出的算法相比于随机选取的特征点进行相对位姿估计精度更高,鲁棒性更强。

随机特征点; 相对位姿估计; 矢量约束; 正交迭代; 未知区域

0　引　言

无人机在执行营救、搜索等任务时,面临着降区地形未知、复杂且无地面辅助导航设备的紧急着陆问题[1]。由于惯性导航存在累计误差、GPS易受干扰,使人机在复杂未知环境中着陆时存在安全隐患。视觉相对导航具有设备简单、信息量大、隐蔽性强、自主性好等优点,在无人机自主着陆/着舰、空中加油及航天器交汇对接[2]等领域都有广泛应用。利用计算机视觉技术引导无人机在未知环境自主着陆是目前的一个研究热点和难点[3-4]。视觉引导无人机自主着陆主要包括以下5个步骤:着降区图像分割、搜索、地质识别、平坦度估计以及无人机与着降区的相对位姿估计[5-7]。其中，如何准确估计出无人机与着降区的相对位姿参数,是保证无人机能够最终安全着陆的关键步骤。

基于合作目标的无人机自主着陆相对位姿估计是通过在无人机降落地点事先布置结构参数已知且地理坐标已标定好的合作目标。然后通过提取合作目标特征点的像素点坐标,在计算机视觉成像原理基础上解决透视N点定位问题。通过求解位姿估计方程来估计出无人机与着降区的相对位姿参数[8-9]。但是，在未知环境中无法提取固定目标的特征点(如Harris角点、尺度不变特征变换(scale-invariantfeaturetransform,SIFT)特征或是其他特征),而目前主要通过两种方式来获得形式上所谓的固定特征点。第1种是基于连续帧的方式,通过帧间特征点匹配,并结合无人机当前高度、飞行距离,实现特征点的标定(特征点的地理坐标),具体可见文献[10];第2种是通过双目立体视觉的方法,可直接重构出着降区的三维坐标信息,实现特征点的标定[11]。然而,在未知区域中提取的特征点存在数量众多、随机性强以及特征点提取误差等因素,因此当利用所有随机特征点进行相对位姿估计时不仅实时性差、而且易造成估计精度不高的问题。文献[12]以星敏感器为研究对象,通过实验指出在估计相对位姿参数时,选取特征点的地理坐标位置对于位姿参数估计精度影响较大,但是文中并未给出特征点应如何选取。针对上述问题,本文提出一种基于矢量约束的随机特征点选取算法,在此基础上利用正交迭代(orthogonaliteration,OI)算法在仿真及物理实验条件下验证所提出算法的有效性。

1　相对位姿估计模型

基于视觉的相对位姿估计主要是通过图像像素坐标系、图像物理坐标系、摄像机坐标系以及一组空间关系已知的特征点坐标系之间的转换关系,推导出相机在合作目标坐标系中的位置和姿态,从而进一步得到相机载体在合作目标坐标系中的位置和姿态[13-14],具体有

(1)

式中,(XL,YL,ZL)、(Xc,Yc,Zc)和(u,v)分别为特征点在世界坐标系下、相机坐标系下以及像素坐标系下的坐标；(u0,v0)为图像物理坐标系原点在图像像素坐标系中的坐标;fx=f/dx,fy=f/dy,f为焦距;dx和dy为一个像素点在x轴和y轴方向的长度;0T=(0,0,0),t=(tx,ty,tz)T是三维平移向量;R是3×3的旋转矩阵,它包含3个独立变量记为滚转角α、航向角γ以及俯仰角β,3个姿态角定义可文献[15],表达式为

(2)

当解算特征点在同一个平面上时,可假设世界坐标ZL=0,将Zc可以看作为比例因子ρ,则式(1)可以改写为

(3)

令

式中,i=1,2,…,N,N为解算特征点个数。式(3)可改写为

ρV=KR1M

(4)

由于K为相机内参构成的矩阵,所以是一个非奇异矩阵,将式(4)两端乘以K-1,化简得

(5)

进一步对式(5)两端乘以MT,并对其两端同时转置,最终得

(6)

2　特征点分布对位姿估计影响分析

2.1位姿估计方程组条件数定义

从位姿估计方程式(6)可以看出,该方程是典型的线性方程组Ax=b形式,其中

(7)

由式(7)可以看出,系数矩阵A是由特征点的地理坐标构成的;b矩阵中包含了摄像机内参、特征点的像素坐标和地理坐标;x为包含所求位姿参数的矩阵。对于线性方程组Ax=b,系数矩阵A的条件数表示为

(8)

其物理意义表示方程组的解对测量数据误差的敏感程度。针对本文的研究问题,假设b中存在误差δb(包括相机参数标定误差,特征点像素提取误差等),得到的解记为x+δx,δx为误差,则线性方程组可表示为

(9)

由式(9)可得

(10)

进一步可推出

(11)

而由方程组Ax=b可知

(12)

因此,根据式(11)和式(12)可得

(13)

通过式(13)可知,如果cond(A)大,则b的微小扰动就能引起解x的较大改变,数值稳定性差。反之,如果cond(A)小,则方程的数值稳定性好,即当有外界扰动时得到的位姿参数精度高且数据稳定性好。

2.2评价指标

(14)

(15)

为了分析特征点分布与相对位姿参数估计精度及稳定性间的关系,引入了3个特征点分布评价指标,即矢量角均分度、矢量模值均值以及最大矢量模值。首先将N个特征点的矢量角按从大到小排列ω={ω1,ω2,…,ωN},对应的矢量模长d={d1,d2,…,dN},3个评价指标分别定义如下。

(1) 矢量角均分度ϖ

(16)

该指标用于描述特征点在平移坐标系中矢量角的均分程度,当N个相邻特征点之间的矢量夹角越接近,其矢量均分度越小。

(17)

该指标用于描述特征点在平移坐标系中矢量模值的平均值。

(3) 矢量模值最大值dmax

(18)

该指标用于描述特征点在平移坐标系中矢量模值中的最大值。

此外,为了整体评价位姿估计精度,引入位置误差εp和角度误差εr,其定义分别如式(19)和式(20)所示。

(19)

(20)

式中,xt，yt和zt分别表示X,Y,Z3个方向上的位置真值;Δx，Δy和Δz分别为3个方向的位置估计误差; Δα，Δβ和Δγ分别表示3个姿态角的误差。

2.3数值分析

假设相机的等效焦距为821,3个姿态角(α,β,γ)分别为10°、20°、-15°,固定平移向量在x、y方向上的分量tx=ty=25,tz=300,在特征点坐标中随机加入不同信噪比噪声来模拟实际提取特征点时的误差,并取信噪比为60 dB。针对以下3种情况,进行了500次的蒙特卡罗仿真相对位姿估计实验,其中位姿估计算法使用的是OI算法[16]。

(1)矢量角均分度对位姿估计精度的影响

以6个特征点为例,解算特征点几种典型分布情况如图1所示。

图1　6个特征点的4种典型分布Fig.1　Four kinds of typical distribution of six feature points

通过计算各评价指标,其结果如表1所示。

表1　6个特征点随机分布时各指标评价结果

从表1可以看出,当条件数小时,位姿估计点误差也小;当矢量模值均值和最大矢量模值一样或相差不大时,矢量角均分度越小的,对应条件数也越小,位姿估计误差也越小。

(2)矢量模值最大值和矢量模值均值对位姿估计精度的影响

随机生成模值相等的6个特征点,如图2(a)所示,保持6个点的矢量角均分度不变,改变其中几个特征点的模值分别如图2(b)～图2(e)所示。

图2　6个特征点的5种典型分布Fig.2　Five kinds of typical distribution of six feature points

计算图2中的各评价指标,其结果如表2所示。

表2　矢量均分度不变情况下各指标评价结果

由表2可看出,当矢量角均分度和矢量模值最大值保持不变时,矢量模值均值小的对应较小的条件数,估计结果误差越小;对比图2(c)和图2(d)可知,当矢量模值平均值也一样时,矢量模值最小模值小的,条件数较小;对比图2(e),当矢量角均分度和矢量模值均值相等时,矢量模值最大值小的,条件数较小。

(3)特征点数对位姿估计精度的影响

在第(1)种情况下所示的4种特征点分布基础上添加同样一个解算点,如图3所示,统计结果如表3所示。

图3　7个特征点的4种典型分布Fig.3　Four kinds of typical distribution of seven feature points

由表3分析可知,当整体分布不变的情况下,添加一个解算点可以使得条件数和解算精度有所改善,但程度有限。此外当特征点个数分别为5～8个、特征点均成正多边形分布且矢量模值最大值相等的情况下,进行了500次蒙特卡罗仿真实验,记录不同特征点个数对解算时间和精度的影响,其结果如表4所示。

表4　实时性比较

从表4中可以看出,随着参与相对位姿估计的特征点数量增加,位姿估计精度也会提高,但是实时性会下降。

通过上述3种情况对相对位姿估计精度的影响分析可知,当矢量角均分度、矢量模值均值及矢量模值最大值越小时,相对位姿估计精度越高。此外,将实时性和位姿估计精度综合考虑,本文选取6个特征点进行相对位姿估计。

3　矢量约束搜索策略

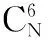
3.1特征点组合生成

本文主要通过对最大矢量模值和矢量角均分度进行约束来提取满足要求的特征点组合。

根据第2节的结论可知,当其他评价指标一定时,最大矢量模值越小时,相对位姿估计精度越高。此外随着无人机的降落,靠近平移坐标系中心点的特征点也不易出视野,所以本文首先对特征点的最大矢量模值进行约束。

其最大模值约束策略如下:选取满足集合

的m个特征点为初选点,其中为着降区半径在图像坐标系中所对应的像素数。由于矢量角均分度对相对位姿估计精度有较大影响,为保证矢量角均分度尽量小,本文对其进一步约束。

最后分别以m个特征点为第一个解算点进行遍历,可生成m组位姿参数估计特征点组合,并计算每个组合的矢量角均分度和矢量模值均值。

3.2矢量约束归一化与最优值计算

在得到用于相对位姿估计的特征点组后,对m组特征点按照如下3个步骤进行求解。

(1) 矢量均分度归一化

将第j组的矢量均分度用ϖj(j=1,2,…,m；i=1,2,…,6)表示,其中最大值为ϖmax,最小值为ϖmin，并对其做线性归一化转化。

(21)

式中,0≤ϖ(j)≤1。

(2)矢量模值均值归一化

(22)

(3) 优先值计算

根据选取策略,设定第j组的优先值为

(23)

式中,j=1,2,…,m。将W(j)从小到大按顺序排列,选取优先值最小的第j组特征点作为解算特征点,来估计无人机的位置与姿态。由于无人机在降落过程中,随着图像尺度变化参与解算的特征点可能存在出视野或是点丢失的情况,同时着降区内也可能出现新的特征点。此时,需要及时更新初选点集合,确保完成相对位姿估计。

3.3算法流程

本文算法计算流程如图4所示。

图4　算法流程图Fig.4　Algorithm flowchart

4　实验结果及分析

4.1仿真实验验证

假设在着降区内有29个特征点,如图5所示。

图5　初始特征点Fig.5　Initial feature points

根据本文所提出的矢量约束选点策略,选取用于相对位姿估计的特征点如图6中用蓝色框选出的解算特征点组合。

图6　矢量约束结果Fig.6　Vector constraint results

为了验证所选取特征点的解算精度,在图5中分别随机选取了2组特征点进行对比解算。设定3个旋转角(α,β,γ)分别为15°、30°、-15°,固定平移向量在x、y方向上的分量tx=ty=25,令tz为变量(相机距离地面的高度),假设信噪比为70dB,对3组特征点分别进行测试,结果如图7所示。

图7　误差结果Fig.7　Error results

由图7可知,在相同信噪比情况下,用矢量约束策略选出的点组合与随机选取点组合相比,位姿解算结果的相对误差更小,尤其在远距离解算时,本文选取的解算点组合在位置解算中获得了更高的精度,具有更好的抗噪性。

4.2物理实验验证

主要的实验设备有:北京博创兴盛科技有限公司生产的UP-VoyagerIIA自主移动机器人;CCD传感器采用罗技C310摄像头(分辨率为640×480,等效焦距为821);实验使用70cm×50cm的坐标纸,代表无人机选定的着降区,记为模拟着降区;并在坐标纸上随机黏贴39个蓝色方格和20个红色方格,方格尺寸为1cm×1cm,同时记录这59个方格的中心坐标,代表已经被标注好的随机特征点,其中黑色原点代表着降区坐标系的原点,完成特征点的标定,相关设备如图8所示。

图8　实验中的相关设备Fig.8　Related equipment in experiments

实验中将相机固定在移动机器人上,使移动机器人距离模拟着降区1.5m处开始不断靠近待选着降点,模拟无人机在着降区域的下降过程。

当移动机器人距离模拟着降区110cm时,摄像机在模拟着降区坐标系下的坐标(单位为cm)记为(x,y,z)=(14.5,6,110),拍摄结果如图9所示。

图9　t3=110 cmFig.9　t3=110 cm

用本文方法对图9中的59个随机特征点(即59个方格的中心坐标)进行计算,得到图10中用蓝色方框标注的解算特征点组合。另外随机选取了2组特征点组合,分别用绿色和红色方框标注,进行后续相对位姿估计精度对比实验。

图10　特征点选取Fig.10　Feature selection

在距离待选特征点60～150cm的范围内,通过改变相机与待选特征点x、y和z 3个方向的偏移量来进行实验测试,图像中特征点的质心像素坐标通过手动标注(运动平台与待选特征点越近,成像的像素分辨率越高,手动标定的像素坐标精度也越高)。将本文方法选取的解算点组合与上述随机选取的2组解算点进行相对位姿估计误差对比分析,相对误差ε定义为

(24)

位置相对误差实验结果如表5所示。

表5　位置相对误差

从表5可以看出,基于矢量约束的随机特征点选取算法,可以自动有效选取特征点组合,且数值稳定性高于随机选取的特征点组合,随着运动平台与待选特征点越近,解算精度越高。而对于其他两组随机选取的特征点由于其中一些特征点出视场,造成无法进行相对位姿估计,所以表5中用“-”来表示。此外需要说明的是，由于移动机器人姿态角控制精度不高,所以实验中未对姿态角误差进行比较。

5　结　论

提出一种基于矢量约束的特征点选取算法,为在未知环境下利用视觉进行相对位姿参数准确、鲁棒估计提供一种有效的解决思路。通过大量仿真实验及物理实验,结果表明，本文提出的算法相比于随机选取特征点进行位姿估计的方法精度更高,鲁棒性更强。

[1]FitzgeraldD,WalkerR,CampbellD.AvisionbasedforcedlandingsiteselectionsystemforanautonomousUAV[C]∥Proc. of the IEEE International Conference on Intelligent Sensors, Sensor Networks and Information Processing, 2005: 397-402.

[2]YangS,SchererSA,ZellA.Anonboardmonocularvisionsystemforautonomoustakeoff,hoveringandlandingofamicroaerialvehicle[J].Journal of Intelligent & Robotic Systems, 2013, 69(1): 499-515.

[3]SchererS,ChamberlainL,SinghS.Autonomouslandingatunpreparedsitesbyafull-scalehelicopter[J].Robotics and Autonomous Systems, 2012, 60(12): 1545-1562.

[4]TakahashiMD,AbershitzA,RubinetsR,etal.Evaluationofsafelandingareadeterminationalgorithmsforautonomousrotorcraftusingsitebenchmarking[J].Journal of the American Helicopter Society, 2013, 58(3): 1-13.

[5]ShenYF,RahmanZ,KrusienskiD,etal.Avision-basedautomaticsafelanding-sitedetectionsystem[J].IEEE Trans. on Aerospace and Electronic Systems, 2013, 49(1): 294-311.

[6]CoombesM,ChenWH,RenderP.ReachabilityanalysisoflandingsitesforforcedlandingofaUAS[J].Journal of Intelligent & Robotic Systems, 2014, 73(1/4): 635-653.

[7]MejiasL,EngP.Controlledemergencylandingofanunpoweredunmannedaerialsystem[J].Journal of Intelligent & Robotic Systems, 2013, 70(1/4): 421-435.

[8]GholamiMR,GeziciS,StromEG.ImprovedpositionestimationusinghybridTW-TOAandTDOAincooperativenetworks[J].IEEE Trans. on Signal Processing, 2012, 60(7): 3770-3785.

[9]ZhangH,JiangZ,ElgammalA.Vision-basedposeestimationforcooperativespaceobjects[J].Acta Astronautica,2013,91(10):115-122.

[10]MaX,ChengYM,HaoS,etal.Densepointfeaturegenerationalgorithmbasedonmonocularsequenceimagesfordepthmeasurementofunknownzone[J].Acta Aeronautica et Astronautica Sinica,2015,36(2):596-604.(马旭,程咏梅,郝帅,等.面向未知区域深度测量的单目序列图像稠密点特征生成算法[J].航空学报,2015,36(2):596-604.)

[11]TheodoreCT,TischlerMB.Precisionautonomouslandingadaptivecontrolexperiment(PALACE),ADM002075[R].California:NationalAeronauticsandSpaceAdministrationAmesResearchCenterMoffettField, 2006.

[12]ZhangL,HeX,WeiZH,etal.Impactanalysisofstardistributiononleastsquareattitudemeasuringprecisioninstarsensor[J].Infrared and Laser Engineering, 2014, 43(6): 1836-1841.(张磊,何昕,魏仲慧,等.星图分布对星敏感器最小二乘姿态精度的影响[J].红外与激光工程,2014,43(6):1836-1841.)

[13]ZhuX,RamananD.Facedetection,poseestimation,andlandmarklocalizationinthewild[C]∥Proc. of the IEEE International Conference on Computer Vision and Pattern Recognition, 2012: 2879-2886.

[14]PauwelsK,RubioL,DiazJ,etal.Real-timemodel-basedrigidobjectposeestimationandtrackingcombiningdenseandsparsevisualcues[C]∥Proc. of the IEEE International Conference on Computer Vision and Pattern Recognition, 2013: 2347-2354.

[15]HaoS,ChengYM,MaX,etal.RobustcornerprecisedetectionalgorithmforvisuallandingnavigationofUAV[J].Systems Engineering and Electronics, 2013, 35(6): 1262-1267.(郝帅, 程咏梅, 马旭, 等. 无人机视觉着舰导航鲁棒角点精确检测算法[J].系统工程与电子技术, 2013, 35(6): 1262-1267.)

[16]LuCP,HagerGD,MjolsnessE.Fastandgloballyconvergentposeestimationfromvideoimages[J].IEEE Trans. on Pattern Analysis and Machine Intelligence, 2000, 23(2):610-622.

Selection algorithm of random feature points based on vector constraints

MA Xu1,2, CHENG Yong-mei1, HAO Shuai2

(1.College of Automation, Northwestern Polytechnical University, Xi’an 710129, China; 2. School of Electrical and Control Engineering, Xi’an University of Science and Technology, Xi’an 710054, China)

Thefeaturepointsoftheextractedimagearecharacterizedbyalargenumberandstrongrandomnesswhenunmannedaerialvehicle(UAV)landingautonomouslyatanunknownzonebyusingvision.Inordertoovercometheproblemsthatrandomlyselectingfeaturepointsforrelativepositionandangleestimationleadstolowprecisionestimationandpoorstability,aselectionalgorithmofrandomfeaturepointsbaseonvectorconstraintsisproposed.Firstly,geographiccoordinatesofthefeaturepointsareconsideredasanimportantfactorwhichaffectstheequationprecisionthroughanalyzingthepositionandattitudeestimationequation.Secondly,thevectorangleaveragedegree,themeanofvectormodulusandthemaximumvalueofvectormodulus,threekindsofconstraintfunctionsareintroduced.Andaselectionstrategyofrandomfeaturepointsbasedonvectorconstraintsisdeveloped.Finaly,theorthogonaliterativealgorithmisusedtoevaluatethepositionandattitudeestimationaccuracyfortheselectedfeaturepoints.Theexperimentalresultsshowthattheproposedalgorithmhashigheraccuracyandstrongerrobustnesscomparedtothemethodofrandomlyselectingfeaturepoints.

randomfeaturepoints;relativepositionandattitudeestimation;vectorconstraints;orthogonaliteration;unknownzone

2015-11-03；

2016-04-27；网络优先出版日期：2016-06-19。

国家自然科学基金(61135001)；西安科技大学博士启动金(2015QDJ007)；西安科技大学培育基金(2014015)；信息融合技术教育部重点实验室开放基金(LIFT2015-G-1)资助课题

TP217.3

ADOI:10.3969/j.issn.1001-506X.2016.10.21

马旭(1985-),女,博士研究生,主要研究方向为视觉导航、模式识别和图像处理。

E-mail:maxucat@gmail.com

程咏梅(1960-),女,教授,博士,主要研究方向为信息融合、目标跟踪、视觉导航。

E-mail:chengym@nwpu.edu.cn

郝帅(1986-),男,讲师,博士,主要研究方向为视觉导航、模式识别和图像处理。

E-mail:hsh000@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160619.0954.002.html