融合粗糙集和扩散二元萤火虫算法的属性约简方法

程美英， 倪志伟， 朱旭辉

(1. 合肥工业大学管理学院， 安徽 合肥 230009； 2. 过程优化与智能决策教育部重点实验室， 安徽 合肥 230009； 3. 新加坡南洋理工大学计算机科学与工程学院计算智能中心实验室， 新加坡 639798)



融合粗糙集和扩散二元萤火虫算法的属性约简方法

程美英1,2,3， 倪志伟1,2， 朱旭辉1,2

(1. 合肥工业大学管理学院， 安徽 合肥 230009； 2. 过程优化与智能决策教育部重点实验室， 安徽 合肥 230009； 3. 新加坡南洋理工大学计算机科学与工程学院计算智能中心实验室， 新加坡 639798)

从一维细胞自动机模型入手，将自然界中种群的扩散行为引入二元萤火虫算法(binary glowworm swarm optimization, BGSO)中，提出了一种扩散二元萤火虫算法 (spread binary glowworm swarm optimization, SBGSO)。该算法对萤火虫个体设置营养值及营养阈值的上下限，然后执行扩散操作，以正态分布方式产生新的个体，并淘汰一些持续表现很差的个体，释放资源给其他个体，以保持种群的动态多样性。然后将SBGSO作为搜索策略，粗糙集 (rough set, RS) 作为评价准则，应用于大数据预处理的属性约简问题。为验证本文算法的可行性，采用5个UCI数据集进行实验，并结合10-fold和支持向量机(support vector machine,SVM)算法对预测结果分类准确率进行分析，通过与其他算法对比,表明本文算法具有较好的约简效果。

二元萤火虫算法； 扩散机制； 一维细胞自动机； 粗糙集； 属性约简

0　引　言

萤火虫算法是一种模拟自然界中萤火虫成虫聚集发光行为的仿生智能算法。目前萤火虫算法主要有两个版本：一种称为GSO(glowworm swarm optimization)[1],另一种称为FA(firefly algorithm)[2]。FA在仿生原理上与GSO大致相似，但具体实现时有一定的差异。萤火虫算法自提出以来，在连续域优化及离散域优化问题[3-6](如：弹道导弹突防、车辆路径规划、多目标优化、函数优化等)中得到较好的应用。“探索和利用”的冲突以及算法初始时刻运行时间过长是萤火虫算法固有的缺陷，为克服其缺点，目前对萤火虫算法的改进策略主要分为以下几个主要方面：①与混沌策略相结合的萤火虫算法。如：文献[7]利用切比雪夫混沌映射初始化萤火虫种群，从而提高初始解的质量；文献[8]对种群中适应值较低的个体进行混沌扰动，从而保持种群的动态多样性；文献[9]采用混沌方法优化局部最优解,从而加快算法的快速收敛。②与调节步长机制相结合的萤火虫算法。如：文献[10-11]将算法中的步长设置成与算法迭代次数相关的函数,并随着迭代次数的增加逐步递减,从而保持全局及局部探索能力的平衡；文献[12]引入个体搜索“成功”或“失败”的概念，当萤火虫个体搜索成功时加大步长，反之缩减步长；文献[13]中算法的步长与邻域内萤火虫个体分布密度相关, 当邻域内萤火虫个体分布稀疏时使用较大步长,反之选择较小的步长以提高解的精度。③与其他群智能算法相结合的萤火虫算法。如与人工鱼群算法[14]、遗传算法[15]、蜂群算法[16-17]、蛙跳算法[18]、杂草算法[19]等结合，实现优势互补。

为拓宽萤火虫算法的应用范围，使其在二元离散优化问题(即一个维数为L的0、1序列表示问题的一个解)中得到较好的应用，本文将二进制编码引入萤火虫算法中，提出了一种新颖的二元萤火虫算法(binary glowworm swarm optimization, BGSO)。 “探索和利用”的冲突是萤火虫算法固有的缺陷，将自然界中种群的扩散行为引入BGSO中，提出了一种基于扩散行为的二元萤火虫算法(spread binary glowworm swarm optimization, SBGSO)。然后将SBGSO与粗糙集(rough set, RS)相结合，应用于大数据预处理中典型二元离散优化问题——属性约简问题。

本文首先简要介绍基本GSO的原理及求解步骤，在此基础上，将模糊函数映射机制引入到GSO中，提出BGSO，并采用一维二值细胞自动机对问题的求解过程进行描述；其次针对BGSO中“早熟”的缺陷，对种群中的萤火虫个体设置营养值及营养阈值，执行扩散及淘汰操作，提出SBGSO，并对该算法的收敛性、复杂度(包括时间复杂度和空间复杂度)进行理论分析；然后将SBGSO作为搜索策略，RS作为子集评估度量准则，应用于求解二元离散优化问题——属性约简问题中；最后对算法进行了仿真实验与对比分析。

1　BGSO

1.1基本GSO

在基本GSO中，初始时刻种群中的萤火虫个体携带等量的荧光素，随机分布在整个搜索空间中。随后萤火虫个体通过追随各自视觉范围内比自身亮的萤火虫进行位置进化，群体更新，最终收敛在最优目标值上。基本步骤如下：

步骤 1根据式(1)将萤火虫i在第t次迭代的位置xi(t)对应的目标函数值J(xi(t))转换成荧光素值li(t)：

(1)

步骤 3按式(2)计算萤火虫i在其动态决策域半径内向萤火虫δ移动的概率Piδ(t)：

(2)

步骤 4萤火虫i移动后，按式(3)更新自身的位置：

(3)

步骤 5按式(4)更新萤火虫i的动态决策域半径：

(4)

循环步骤1～步骤5，萤火虫个体最终收敛在全局最优解上。其中，ρ为荧光素挥发系数；μ为荧光素更新率；Ni(t)为萤火虫i决策域内的萤火虫个数；η为动态决策域更新率；nt为领域集内所含萤火虫数目的阈值；s为移动步长；rs为萤火虫个体的感知半径[1]。

1.2BGSO一维细胞自动机模型

为更好地将萤火虫算法应用于二元离散优化问题，引入二进制编码，并采用一维二值细胞自动机模型对问题的复杂求解过程进行描述，如图1所示。

图1　一维二值萤火虫算法细胞自动机模型Fig.1　One-dimensional two values glowworm swarm optimization cellular automata model

(5)

任意时刻t，萤火虫从初始细胞出发遍历图1，按式(5)随机从细胞状态集合中选择0或1。一次遍历结束后所得的0/1序列即对应问题的一个解。在上述离散化机制中，模糊函数将连续空间内移动的萤火虫个体位置离散化，从而达到求解具有0/1特性的二元离散型优化问题的目的。

2　SBGSO

算法的“早熟收敛”是萤火虫算法固有的缺陷。在BGSO的运行初期，种群中的超级个体因具有较强的亮度而吸引其他个体迅速向其周围靠拢，种群多样性丧失，算法早熟收敛。因而提高种群的多样性，使得种群在求解问题中保持持续优化能力是改进BGSO的有效途径。

在生物的进化过程中，由于生存环境的压力(如食物的匮乏、种群外部竞争等)、种群自身密度的制约以及生境的斑块化都会导致生物个体从一个生境转移到另一个生境中， 这不仅可以维持生态系统的平衡稳定，还可以进一步防止物种的灭绝[20]。受此启发，在本节中，将自然界中种群扩散行为引入BGSO中，提出了SBGSO。

2.1SBGSO主要思想

2.1.1种群初始化

令初始种群规模为gsonum，[Xmin,Xmax]为搜索空间范围。初始时刻，按式(6)随机产生萤火虫个体的初始位置xij(0)(xij(0)∈[Xmin,Xmax])，其中rand()为随机数。

xij(0)=(rand()/Rand_Max+1.0))×

(6)

2.1.2种群扩散

(7)

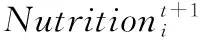
(8)

新个体的位置设置如文献[21]所示，以父代为轴线，将子代按正态分布方式扩散在L维空间中，设最大、最小方差分别为τ0和τf，当前迭代次数为Iter，最大迭代次数为Maxiter。因正切函数tan()的值随着自变量的减小而逐步递减，根据正切函数的特点，得到：

(9)

则由父代个体i产生的子代位置为

(10)

由式(9)和式(10)可以看出：开始时，τ值较大，子代萤火虫个体距离父代较远，而后期τ值随着迭代次数Iter的增加而逐步递减，子代萤火虫个体分布在离父代个体较近的位置。这就使得子代个体能比较均匀地分布在父代周围，拓宽了萤火虫个体的搜索范围。

2.1.3种群淘汰

经过扩散操作之后，种群的规模扩大，达尔文曾指出：没有一个自然种群能无限制地增长。种群在增长过程中会遇到来自方方面面的环境阻力，如种群规模制约、食物浓度制约和竞争强度制约。

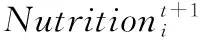
2.2SBGSO主要步骤

本文SBGSO的主要步骤如下：

步骤 1初始化萤火虫个体荧光素值、位置、决策域半径、营养值、个体自身最优值、全局最优值及全局最差值等；

步骤 2萤火虫个体遍历图1一维二值细胞自动机模型，按式(5)随机选择0或1；

步骤 3每次迭代之后，计算每只萤火虫个体所对应0/1序列的适应值，并与自身最优值进行对比，按式(7)对自身营养值进行更新；

步骤 4将萤火虫个体自身营养值与Nup及Ndown进行对比，进行淘汰或扩散操作；

步骤 5扩散操作，根据式(8)确定产生的子代数目，按式(9)和式(10)确定子代位置，并计算子代适应值；

步骤 6综合比较父代和子代个体的适应值，得到全局最优值和全局最差值；

步骤 7萤火虫个体按式(1)～式(4)进行移动，并对荧光素、位置及个体决策域半径进行更新；

步骤 8循环步骤3～步骤7，若满足循环结束条件，转至步骤9，不满足继续；

步骤 9输出全局最优结果。

2.3SBGSO收敛性证明

本小节先通过建立BGSO对应的吸收态Markov过程模型，进而证明本文提出的SBGSO以概率1收敛。

证毕

证明由全概率式可得，对于∀t=1,2,…，有

则有

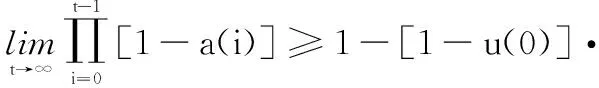
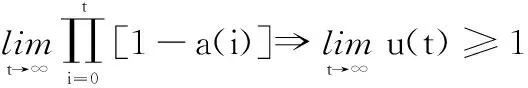
证毕

定理 1当t→∞时，SBGSO以概率1收敛到全局最优解。

证明假设搜索解空间Ω被划分为n×m个小区间，则Ω=Z1∪Z2∪…∪Zn，且Zb=z1∪z2∪…∪zm(b=1,2,…，n)。设定n,m值时，令n,m足够大，从而确保每个小区间中只有唯一局部最优解。

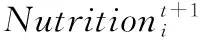
(2) 淘汰操作。当萤火虫个体自身营养值低于Ndown时，则淘汰该萤火虫，表明该区域相对于上一次迭代，没有出现更优的解。

综上分析：当t→∞时，萤火虫个体通过扩散及淘汰操作，可以遍历整个搜索解空间，故本文提出的SBGSO算法能以概率1收敛到全局最优解。

证毕

2.4SBGSO时间复杂度分析

假设初始时刻，子种群的规模为gsonum，L为细胞阵列长度。由第2.2节算法主要步骤可逐步得出SBGSO算法的时间复杂度。

因种群规模为gsonum，步骤1中初始化每只萤火虫个体的荧光素值、决策域半径、初始营养值及自身最优解的时间复杂度均为O(gsonum)，初始化萤火虫个体实数位置所需时间为gsonum·L，时间复杂度为O(gsonum·L)，其他参数初始化时间复杂度为O(1)；步骤2中gsonum只萤火虫个体遍历图1随机选择0或1，时间复杂度为O(gsonum·L)；步骤3将每次迭代之后的实数位置转换成0/1序列，时间复杂度为O(gsonum·L)，求解种群中所有萤火虫个体的适应值，时间复杂度为O(gsonum·L)，比较个体适应值与自身最优适应值时间复杂度为O(gsonum)，更新自身营养值时间复杂度为O(gsonum)；步骤4中将每只萤火虫个体自身的营养值与营养阈值的上限Nup和下限Ndown进行对比,时间复杂度为O(gsonum)；步骤5中假设每次迭代时，有α个父代需要进行扩散操作，γ只萤火虫执行淘汰操作，且α个父代每次产生的所有子代个数总和为Nω，当进行扩散操作时，初始化子代个体营养值时间复杂度为O(Nω)，产生子代个体实数位置的时间复杂度为O(Nω·L)，将子代实数位置转换成0/1序列时间复杂度为O(Nω·L),计算子代个体适应值时间复杂度为O(gsonum·L)，γ只萤火虫执行淘汰操作时间复杂度为O(γ·L)；步骤6中综合比较父代和子代的适应值，得到全局最优解及全局最差解的时间复杂为O((gsonum+Nω-γ)·L)；步骤7中萤火虫荧光素更新时间复杂度为O(gsonum+Nω-γ)，位置更新时间复杂度为O((gsonum+Nω-γ)·L)，个体决策域半径更新时间复杂度O((gsonum+Nω-γ)·(gsonum+Nω-γ))；步骤8对gsonum+Nω-γ只萤火虫个体判断是否满足结束条件，需要的时间复杂度为O(gsonum+Nω-γ)；步骤9输出全局最优解的时间复杂度为O(1)。

因本文算法经过扩散或淘汰操作之后，种群中萤火虫数目时刻都在变化。假设处于饱和状态时，种群规模为gsonum+Nω-γ，则算法经过Maxiter次迭代后，SBGSO算法时间复杂度为

T=O(Maxiter·(gsonum+Nω-γ)·L)

(11)

2.5SBGSO空间复杂度分析

存储每只萤火虫个体的荧光素值及决策域半径所需空间均为gsonum；存储长度为L的实数位置所需空间为gsonum·L；存储每只萤火虫个体的0/1序列所需空间为gsonum·L；记录萤火虫个体自身最优解所需空间为gsonum；记录萤火虫个体自身最优解所对应的0/1序列所需空间为gsonum·L；记录种群最优个体及最差个体所对应的0/1序列所需空间均为L；记录Nω只新萤火虫执行扩散操作所需的存储空间为Nω+Nω+Nω·L，γ只萤火虫执行淘汰操作会释放出γ+γ+γ·L个空间；存储其他参数所需空间为常数；则经过上述分析，整个计算过程所需的存储空间为

(12)

3　SBGSO融合RS求属性约简问题

3.1属性约简优化目标

定义 4设S=为一决策表信息系统，U为论域，C为条件属性集合，D为决策属性集合；V=Ur∈AVr为属性值集合，Vr表示属性r∈A值域，f:U×A→V为信息函数[23]。

定义 5给定S=(U,A),U为论域，若B⊆A,且B≠∅,B上的不可分辨关系IND(B)指B中所有等价关系的交集∩B也是一个等价关系[23]。

定义 6给定S=，对于不可分辨关系B⊆A及任一子集X⊆U，B-(X)=:{x|(x∈U∧[x]B∩X≠∅)}和B-(X)={x|(x∈U∧[x]B⊆X)}分别表示X的上、下近似集,集合BNB(X)=B-(X)-B-(X)称为X的B边界，[X]B表示U中所有与x的不可分辨关系IND(B)[23]。

定义 7设近似空间P为k=(U,R)，Q∈R称知识Q以依赖度k(0≤k≤1)依赖于知识P，即P⟹Q,当且仅当

(13)

式中，card表示集合的基数；posP(Q)为Q的P正域。

假设L为原始数据集中的属性个数，ν为约简后的属性个数，本文的目标为：①约简后所得的属性必须满足分类质量；②约简后的属性个数必须尽量少，即

(14)

式中，k(0≤k≤1)表示决策属性对条件属性的依赖度。

3.2基于ASDM属性依赖度求解算法

为求解属性的依赖度，采用文献[24]提出的属性集合依赖度算法(attribute sets dependability method, ASDM),其求解步骤如下：

步骤 1将条件属性集P作等价类划分，得等价类γ；

步骤 2将决策属性集作等价类划分,得等价类Ψ；

步骤 3求γ∩Ψ的元素数，即card()；

步骤 4k=rP(Q)={card()|{γ∩Ψ}}/{对象个数}。

3.3SBGSO融合RS求解属性约简主要步骤

本小节将第2节提出的SBGSO结合RS,求解属性约简问题。令原始数据集属性个数为L，则图1的一维细胞自动机长度为L。细胞状态Q={0,1},萤火虫从起始细胞出发,从左向右遍历一维细胞自动机,随机选择0或1,1表示该属性被选择核属性,0表示该属性不是核属性,如0/1序列 (1,0,0,1,0,0,0,1) 表示原始属性集中第1,4,8属性为核属性。然后利用ASDM算法计算每只萤火虫个体所对应0/1序列的属性依赖度，进而得出萤火虫个体的适应值。

步骤 1初始化萤火虫位置、荧光素值、决策域半径、个体营养值及营养阈值上下限等参数；

步骤 2设条件属性个数为L，则细胞自动机长度设为L，细胞状态Q={0,1},萤火虫个体遍历图1一维二值细胞自动机模型，随机选择0或1，1表示该属性为核属性，反之0不是；

步骤 3每次迭代之后，利用ASDM算法计算核属性的属性依赖度，计算每只萤火虫个体所对应0/1序列的适应值，并将该适应值与自身最优值进行比较，更新自身营养值；

步骤 4将每只萤火虫个体自身营养值与营养阈值的上限Nup和下限Ndown进行对比，进行淘汰或扩散操作；

步骤 5扩散操作，确定扩散操作后产生的子代数目，确定子代位置，并给子代个体赋予营养值初始值，最后计算子代个体适应值；

步骤 6综合比较父代和子代适应值，得到全局最优值和全局最差值；

步骤 7萤火虫荧光素、位置及个体决策域半径更新；

步骤 8循环步骤3～步骤7，若满足循环结束条件，转至步骤9，不满足继续；

步骤 9输出全局最优值。

4　仿真实验

4.1实验设置

4.1.1实验环境设置

本文所涉及的所有实验均采用VC6.0编写，编译运行的PC机参数为32位Windows 7操作系统Intel(R) Core(TM) i5-3470 CPU, 3.20 GHz。

4.1.2参数设置说明

算法中各参数设置如下：Xmax=5，Xmin=-5，li(0)=5.0，μ=0.6，ρ=0.4，s=0.03，η=0.08，nt=5，τ0=3，τf=0.5，初始决策域半径为1.0，最大决策域半径为3.0。种群规模gsonum及运行代数的设置一般与问题的规模成正比。营养阈值的上限Nup和下限Ndown的设置根据具体问题进行自适应调整(如在求解Breast Cancer数据集时，Nup=10，Ndown=1)。

4.2测试数据

为了验证本文算法的可行性和有效性，选用UCI中的5个数据集进行实验(见表1)。在利用本文算法时，不考虑类别数。在UCI数据集中，Breast Cancer的实例数总共有699个，但因其中16个实例缺失属性值，在实验中将该16个实例剔除，剩余683个；剩余数据集Bupa, Wine, Iris, Contraceptive均无属性值缺失。

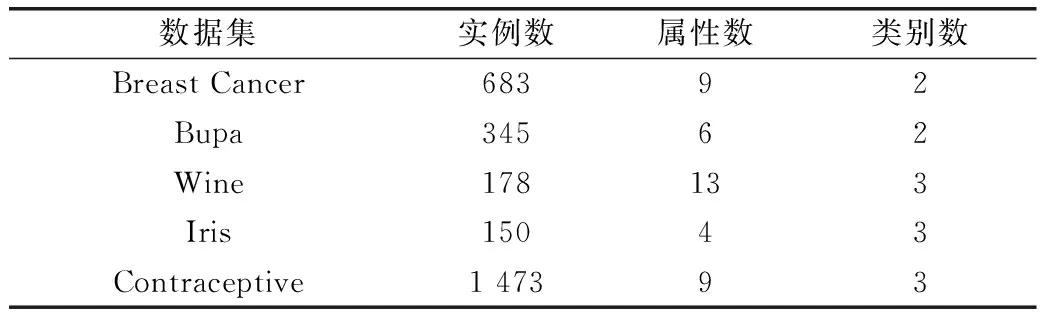
表1　测试数据集

4.3实验结果分析

4.3.1属性约简率及对比实验

运用本文SBGSO结合RS，属性约简结果见表2。其中，属性约简率为((L-ν)/L)×100%。对比分析文献[22,25]，如表3所示：本文算法除Wine数据集在约简率上稍微低于文献[25]，其他数据集的约简率均等于或大于文献[22,25]。同样对比分析文献[26-27]，如表4所示：本文算法在数据集Wine和Iris上的属性约简率大大高于乐观多粒度模糊粗糙集约简算法、悲观多粒度模糊粗糙集约简及一致性准则属性约简算法。

表2　本文方法属性约简结果

表3　多种方法属性约简结果对比分析(1)

表4　多种方法属性约简结果对比分析(2)

4.3.2分类准确率及对比实验

在采用SBGSO结合RS进行属性约简后，继续采用中国台湾学者Chih-Jen Lin提供的LIB-SVM (www.csie.ntu.edu.tw/～cjlin/libsvm)算法结合10-fold交叉验证分析属性约简前后的分类准确率，选择径向基核函数(radial basis function,RBF)为支持向量机(support vector machine,SVM)的核函数，最优参数c∈[2-5,215]，g∈[2-15,23]的值利用网格搜索法选取，实验结果如表5所示。

表5　属性约简分类准确率分析

运用本文方法，Bupa属性子集的最优分类准确率和平均分类准确率均有所提高，分别上升了2.462 1%和0.692 4%；Wine和Iris属性子集的最优分类准确率与原始数据集基本保持一致，而平均分类准确率分别上升了6.816 4%和1.867 1%；Breast Cancer和Contraceptive的最优分类准确率和平均分类准确率有轻微下降。

在现有文献中，将群智能算法与相应子集评估度量准则相结合来求解属性约简的方法较多。如文献[22]结合基于生命周期的二元蚁群算法和分形维数应用于属性约简，文献[25]结合改进的离散型萤火虫算法和分形理论求解属性约简问题，而本文以SBGSO作为搜索策略、RS作为子集评估度量准则。表6将本文实验结果与文献[22,25]进行对比，进一步体现了本文算法的优越性。

表6　文献[22,25]方法与本文方法对比结果

由表6可知，针对数据集Wine和Iris，本文算法具有更好的最优分类准确率和平均分类准确率；而数据集Bupa和Contraceptive属性子集的最优分类准确率及平均分类准确率均高于文献[22]，但均略低于文献[25]；数据集Breast Cancer的最优分类准确率与文献[22,25]一致，但平均分类准确率略低于文献[22,25]。

5　结束语

本文主要工作如下：①从一维细胞自动机模型入手，将BGSO归结到一维二值细胞自动机这一框架之下，不仅很好地解决了带0/1特性的二元离散优化问题，而且体现了计算的本质；②将自然界中种群扩散行为引入BGSO中，提出了SBGSO，保持了种群的动态多样性，平衡了算法“探索和利用”的冲突；③属性约简在大数据预处理中起着十分重要的作用，本文将SBGSO与RS相结合，为大数据的预处理提供了一种新颖的方法。因生物扩散在自然生态系统中随处可见，下一步的工作将继续研究生态系统中种群的扩散动力学，并将其引入到其他群智能算法中，以弥补算法的“早熟”缺陷。

[1] Krishnanand K N, Ghose D. Glowworm swarm optimisation:a new method for optimising multimodal functions [J].InternationalJournalofComputationalIntelligenceStudies, 2009, 1(1):93-119.

[2] Yang X S.Nature-inspiredetaheutisticalgorithms[M]. London: Luniver Press, 2008.

[3] Jayakumar D N, Venkatesh P. Glowworm swarm optimization algorithm with topsis for solving multiple objective environmental economic dispatch problem [J].AppliedSoftComputing, 2014, 23(10):375-386.

[4] Wu B, Qian C H, Ni W H, et al. The improvement of glowworm optimization for continuous optimization problem [J].ExpertSystemwithApplications, 2013, 39(7): 6335-6342.

[5] Du P Z, Tang Z M, Lu J F, et al. Global path planning for ALV based on improved glowworm swarm optimization under uncer-tain enviroment [J].ActaElectronicaSinica, 2014,42(3):616-624.(杜鹏桢,唐振民, 陆建峰,等.不确定环境下基于改进萤火虫算法的地面自主车辆全局路径规划方法[J]. 电子学报, 2014,42(3):616-624.)

[6] Fan Y S, Wang M L, Wen M M, et al. Analysis of ballistic missile penetration effectiveness based on FA-AHP [J].SystemsEngineeringandElectronics,2015, 37(4): 845-850. (范阳寿,汪民乐,文苗苗,等.基于萤火虫算法层次分析法的弹道导弹突防效能分析[J]. 系统工程与电子技术, 2015,37(4): 845-850.)

[7] Yu S H, Su S B. Research and application of chaotic glowworm swarm optimization algorithm[J].JournalofFrontiersofComputerScienceandTechnology,2014,8(3):352-357.(郁书好, 苏守宝. 混沌萤火虫优化算法的研究及应用[J]. 计算机科学与探索, 2014,8(3):352-357.)

[8] Xu H L, Su S B, Yan R R, et al. A firefly algorithm with chaotic diversity control [J].JournalofUniversityofScienceandTechnologyofChina, 2014,44(7):612-617. (徐华丽,苏守宝, 严仍荣, 等. 一种混沌多样性控制的萤火虫优化算法[J]. 中国科学技术大学学报, 2014，44(7):612-617.)

[9] Zhang J L, Zhou G, Zhou Y Q. A new artificial glowwarm optimization algorithm based on chaos method [J].AdvancesinIntelligentandSoftComputing, 2010, 82: 683-693.

[10] Yu S H, Yang S L, Su S B. A improve glowworm swarm optimization with adaptive step[J].Mini-microSystems, 2014，35(6): 1396-1400. (郁书好, 杨善林, 苏守宝. 一种改进的变步长萤火虫优化算法[J]. 小型微型计算机系统, 2014，35(6): 1396-1400.)

[11] He L F, Tong X, Huang S W. Glowwarm swarm optimization algorithm based on hierarchical multi-subgroups[J].JournalofInformation&ComputationScience, 2013,10 (4): 1245-1251.

[12] Huang Z X, Zhou Y Q. Adaptive glowwarm swarm optimization algorithm with changing step for optimizing multimodal functions [J].ComputerEngineeringandApplication, 2012, 48(8):43-47. (黄正新, 周永权. 一种变步长自适应萤火虫群多模态函数优化算法[J]. 计算机工程与应用,2012,48(8):43-47.)

[13] Huang Z X, Zhou Y Q. Self-adaptive step glowworm swarm optimization algorithm for optimizing multimodal function[J].ComputerScience, 2011, 38(7): 220-224. (黄正新,周永权.自适应步长萤火虫群多模态函数优化算法[J].计算机科学,2011, 38(7):220-224.)

[14] Li Y M, Zhou Y Q, Yao X G. Improved glowwrom swarm optimization based on the behavior of follow[J].ComputerScience, 2011,38(3): 248-251. (李咏梅,周永权,姚祥光. 基于追尾行为的改进型人工萤火虫群算法[J],计算机科学,2011, 38(3): 248-251.)

[15] Du X X, Zhang J F, Sun M. Artificial glowworm swarm optimization algorithm based on adaptive distribution mixed mutation[J].JournalofComputerApplications, 2013, 33(7): 1922-1925, 1972.(杜晓昕,张剑飞,孙明.基于自适应t分布混合变异的人工萤火虫算法[J].计算机应用，2013,33(7)：1922-1925,1972.)

[16] Wu B, Cui Z Y, Ni W H. Hybrid swarm intelligence behavior [J].ComputerScience, 2012, 39(5):198-200. (吴斌,崔志勇,倪卫红.具有混合群智能行为的萤火虫群优化算法研究[J].计算机科学,2012, 39(5):198-200.)

[17] Wu Bin, Qian C H, Ni W H. Glowworm swarm optimization for cross dock scheduling problem[J].ComputerEngineeringandApplication, 2013, 49(6): 39-42,51. (吴斌,钱存华,倪卫红.萤火虫群优化算法在越库调度问题中的应用[J].计算机工程与应用,2013, 49(6): 39-42,51.)

[18] Li Y. Leapfrog firefly algorithm and application in dispatch of power system containing wind farm [D]. Shanghai: East China University of Science, 2013. (李洋.蛙跳萤火虫算法及其在含风电场的电力系统调度中的应用[D].上海：华东理工大学，2013.)

[19] Wang Y J. Hybrid artificial fireflies swarm optimization algorithm and its application [D]. Guangxi：Guangxi University of Nationalities, 2012.(王迎菊.混合型人工萤火虫群优化算法及应用研究[D]. 南宁：广西民族大学，2012.)

[20] Zhang L. The study of dispersal population dynamics [D]. Xinjiang： Xinjiang University, 2007. (张龙. 扩散种群的动力学模型研究[D].乌鲁木齐: 新疆大学, 2007.)

[21] Sang H Y, Pan Q K. A discrete invasive weed optimization algorithm for the integrated lot-streaming flow shop scheduling problem [J].ControlTheory&Applications，2015, 32 (2): 246-250. (桑红燕,潘全科.求解流水车间批量流集成调度的离散入侵杂草优化算法[J].控制理论与应用,2015, 32(2): 246-250.)

[22] Cheng M Y, Ni Z W, Zhu X H. Lifecycle-based binary ant colony algorithm [J].PatternRecognitionandArtificialIntelligence, 2014, 27(11): 1005-1014. (程美英,倪志伟,朱旭辉.基于生命周期的二元蚁群优化算法[J].模式识别与人工智能,2014, 27(11): 1005-1014.)

[23] Xu X S, Chen R Y. Attribute decision reduction method based on hybrid rough sets and niche immune optimization[J].ActaElectronicaSinica,2014,42(8):1545-1550.(徐雪松,陈荣元.融合粗糙集与小生境免疫优化的属性约简方法[J].电子学报, 2014, 42(8):1545-1550.)

[24] Meng Q Q, Mei C H. Research on a new dependability of attribute sets [J].ComputerApplication, 2007, 27(7):1748-1750. (孟庆全,梅灿华.一种新的属性集依赖度[J].计算机应用,2007, 27(7):1748-1750.)

[25] Ni Z W, Xiao H W, Wu Z J, et al. Attribute selection method based on improved discrete glowworm swarm optimization and fractal dimension [J].PatternRecognitionandArtificialIntelligence, 2013, 26(12): 1169-1178. (倪志伟，肖宏旺，伍章俊，等. 基于改进离散型萤火虫群优化算法和分形维数的属性选择方法[J]. 模式识别与人工智能, 2013, 26(12): 1169-1178.)

[26] Cui Y J. Multi-granularity rough set in incomplete information systems theory and reduction research [D]. Nanjing: Nanjing University of Science & Technology, 2014. (翟永健.不完备信息系统中多粒度粗糙集理论与约简研究[D]. 南京：南京理工大学，2014.)

[27] Yang M. A novel algorithm for attribute reduction based on consistency criterion [J].ChineseJournalofComputers, 2010, 33(2): 231-239. (杨明.一种基于一致性准则的属性约简算法[J].计算机学报,2010, 33(2): 231-239.)

Attribute reduction method combined with spread binary glowworm swarm optimization and rough set

CHENG Mei-ying1,2,3, NI Zhi-wei1,2, ZHU Xu-hui1,2

(1. School of Management，Hefei University of Technology， Hefei 230009, China; 2.Key Laboratory ofProcessOptimizationandIntelligentDecision-Making，MinistryofEducation，Hefei230009,China;3.ComputationalIntelligenceLab,SchoolofComputerScienceandEngineering,NanyangTechnologicalUniversity,Singapore639798)

Starting from the one-dimensional cellular automata model, the spread mechanism is introduced to binary glowworm swarm optimization (BGSO), and a spread binary glowworm swarm optimization (SBGSO) is proposed. In SBGSO, nutrition value and nutrition threshold is involved to each glowworm, then the spread operation is performed to produce offspring by using the method of normal distribution. Additionally, the individuals who continue to perform poorly are eliminated. The aforementioned operations can largely keep the diversity of the whole populations. After that, SBGSO is combined with rough set (RS) to handle the attribute reduction problem. When dealing with the attribute reduction problem, SBGSO is taken as a kind of search strategy and RS is taken as the evaluation criteria for attribute subsets. To analyze the feasibility and effectiveness of the proposed method, five UCI datasets are used to conduct experiments. Moreover, the 10-fold and SVM are involved to analyze the classification accuracy, experimental results show that the method has relatively higher reduction rate compared with other methods.

binary glowworm swarm optimization (BGSO); spread mechanism; one-dimensional cellular automata; rough set (RS); attribute reduction

2015-10-09；

2016-06-20；网络优先出版日期：2016-07-20。

TP 301.6

A

10.3969/j.issn.1001-506X.2016.10.32

程美英(1983-)，女，博士研究生，主要研究方向为计算智能、数据挖掘。

E-mail:qyc12117@126.com

倪志伟(1963-)，男，教授，博士研究生导师，主要研究方向为数据挖掘、机器学习、人工智能。

E-mail:zhwnelson@163.com

朱旭辉(1991-)，男，博士研究生，主要研究方向为进化计算、数据挖掘。

E-mail:943177204@qq.com

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN.20160720.1114.004.html