工业机器人的线性解耦控制联合仿真研究

汪　坤，梁艳阳，刘宏伟

（1.西南科技大学 信息工程学院，绵阳 621010；2.特殊环境机器人技术四川省重点实验室，绵阳 621010）

工业机器人的线性解耦控制联合仿真研究

汪坤1，2，梁艳阳1，2，刘宏伟2

（1.西南科技大学 信息工程学院，绵阳 621010；2.特殊环境机器人技术四川省重点实验室，绵阳 621010）

为了实现机器人高速高精度的运动，提高机器人的运动稳定性能和跟踪性能，以六自由度串联机器人为研究对象，采用基于牛顿欧拉方法的线性解耦控制方案实现机器人的运动控制，然后在MATLAB/Simulink上分别建立关节空间和笛卡尔空间的系统控制框图，并进行联合仿真。仿真结果表明，采用该控制方案，机器人跟踪性能良好，稳定性高。

工业机器人；牛顿欧拉；线性解耦；联合仿真

0　引言

六自由度串联工业机器人系统是一个非线性、强耦合的多输入多输出高度复杂的机电系统［1］。若是按照传统的设计方式，先建造出实体样机，然后不断的对其进行测试和改进，这种方法会浪费大量的时间和精力。因此需要在制造实体样机之前，设计一个六自由度机器人的虚拟样机系统［2］，模拟机器人的运动和状态。

诸多学者从不同的研究角度出发进行联合仿真的尝试，并取得了比较丰硕的成果。胡蕴博采用PID控制的方式建立了四自由度串联机器人模型并进行了联合仿真［3］；马如奇等人采用PD控制方式建立了四自由度串联机器人模型并进行联合仿真［4］；李月月等人采用PD控制方式建立了Puma560机器人模型并进行联合仿真［5］，文献［6～8］也对机器人的联合仿真进行了研究。分析以上各种方法，多集中在传统的PID控制方式进行联合仿真的研究上，并没有涉及到动力学计算。动力学分析方法种类繁多，有拉格朗日法、牛顿欧拉法、凯恩法等方法，牛顿欧拉方程是基于运动坐标和达朗贝尔建立起来的，没有多余信息，计算速度快，是至今最为有效的逆动力学数值算法之一［9］。因此，本研究将采用牛顿欧拉方法计算各个关节的驱动力矩并结合MATLAB和ADAMS进行联合仿真实时查看机器人运动状态。

1　机器人模型建立

本研究创建一个六自由度串联机器人模型作为研究对象。首先从ADAMS的固件库中选取一些组件作为机器人的主体，如图1所示。然后为其添加约束和驱动，由于本研究对象采用的是各关节均为旋转关节的机器人对象，所以为其各个关节添加转动副和转动副约束；同时将基座固定在大地上，为其添加固定副。另外，在图1中可以看出第五关节向下倾斜45°，主要是为了避免在任务空间中联合仿真时第五关节和第六关节角度同时为0°导致奇异。

图1　六自由度串联机器人ADAMS模型

应用D-H参数法［10］对上述机器人模型进行建模得到其D-H参数如表1所示。

2　控制系统的建立

整个线性解耦控制系统是通过牛顿欧拉方程根据给定的轨迹实时计算出一组驱动力矩，然后由该组驱动力矩来驱动机器人按照给定的运行轨迹进行运动。

表1　六自由度串联机器人D-H参数

为理解基本的机器人控制问题，引出了机器人动力学方程的一般形式，如下所示：

其中Γ表示关节力矩，A（q）表示机器人的惯性矩

2.1关节空间线性解耦控制方法

关节空间中的线性解耦控制又分为两种控制方案：轨迹跟踪控制和位置控制。

在运动过程中给出各个关节在关节空间的理想位置、速度和加速度为轨迹跟踪控制，它适用于各关节的运动轨迹预先确定的情况。轨迹跟踪控制确定w（t）的方程如下所示：

Kp和Kd为调节增益，整个轨迹控制的框图如图2所示。

图2　关节空间中轨迹跟踪控制系统框图

综合式（3）和图2可知，轨迹控制方案主要是通过对关节角度误差和关节角速度误差进行PD调节，进而控制关节加速度，实现机器人准确跟踪、稳定快速运行。

2.2任务空间线性解耦控制方法

任务空间线性解耦控制即任务空间轨迹跟踪控制。类似于关节空间轨迹控制，任务空间轨迹控制主要是控制机器人末端加速度。任务空间的力矩计算方式如下所示：

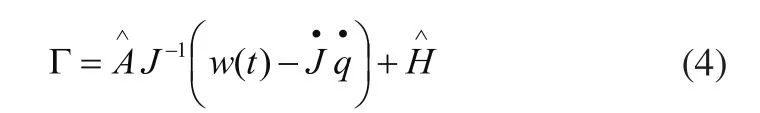
对于带PD控制器的轨迹跟踪控制，其控制方程如下：

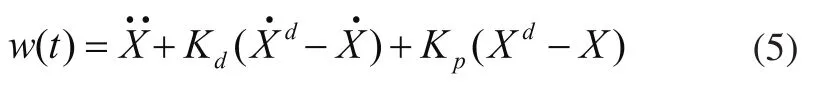
在任务空间中的控制框图如图3所示。

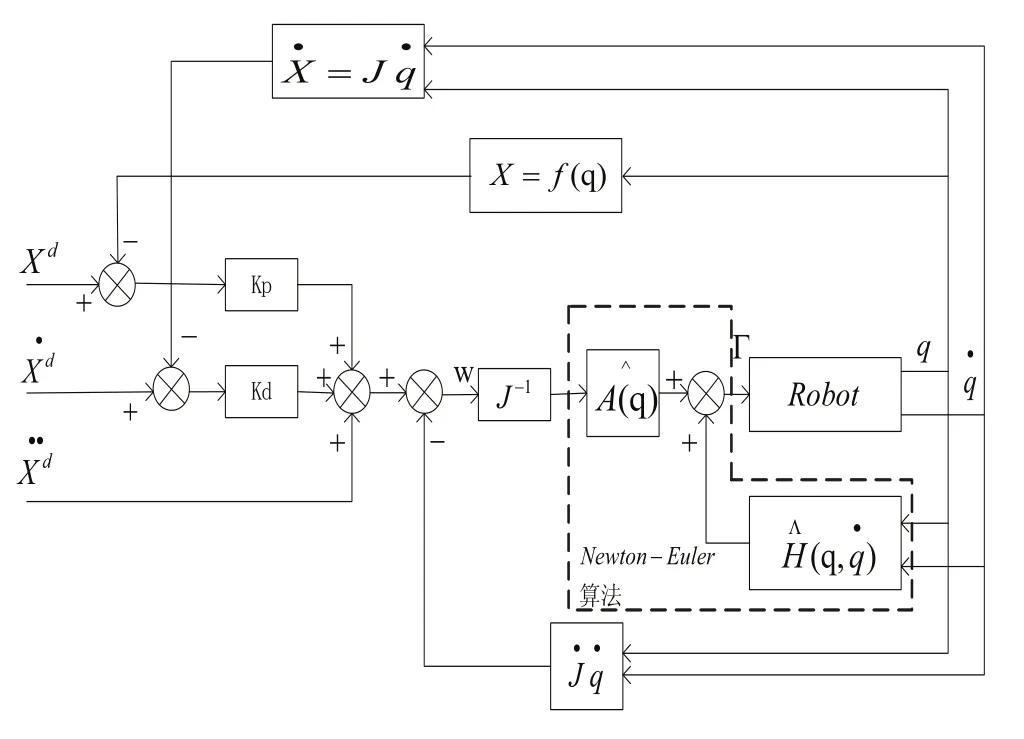
图3　任务空间中线性解耦控制框图

3　联合仿真系统实验

为了验证该方法的控制效果，分别在关节空间和任务空间中规划出机器人的运动轨迹，测试其跟踪性能和稳定性能。

3.1关节空间中的仿真

以轨迹跟踪控制为例，给定机器人的六个关节期望运动的目标角度分别为pi/2，pi/3，-pi/2，pi/4，5*pi/12，pi/5。其仿真结果如图4所示。

如图4所示，关节5在t∈（0，0.005）区间内存在误差突变，导致这一问题的主要原因是由于ADAMS返回角度时存在延迟，进而造成了第五关节pi/4的角度偏差。另外，在t∈（0.005.3）区间内，各关节角度的跟踪误差在0.1rad内。以上对比表明基于牛顿欧拉方法的线性解耦控制方案具有很好的跟踪性能。

3.2任务空间中的仿真

同在关节空间类似，任务空间中首先给定起始位姿和目标位姿，仿真结果如图5所示。

图4　关节角度误差

图5　规划末端位置和实际末端位置

通过图5和图6可以看出，在机器人运动过程中，规划的末端位置和姿态与实际末端位置和实际的末端位置和姿态高度重合。

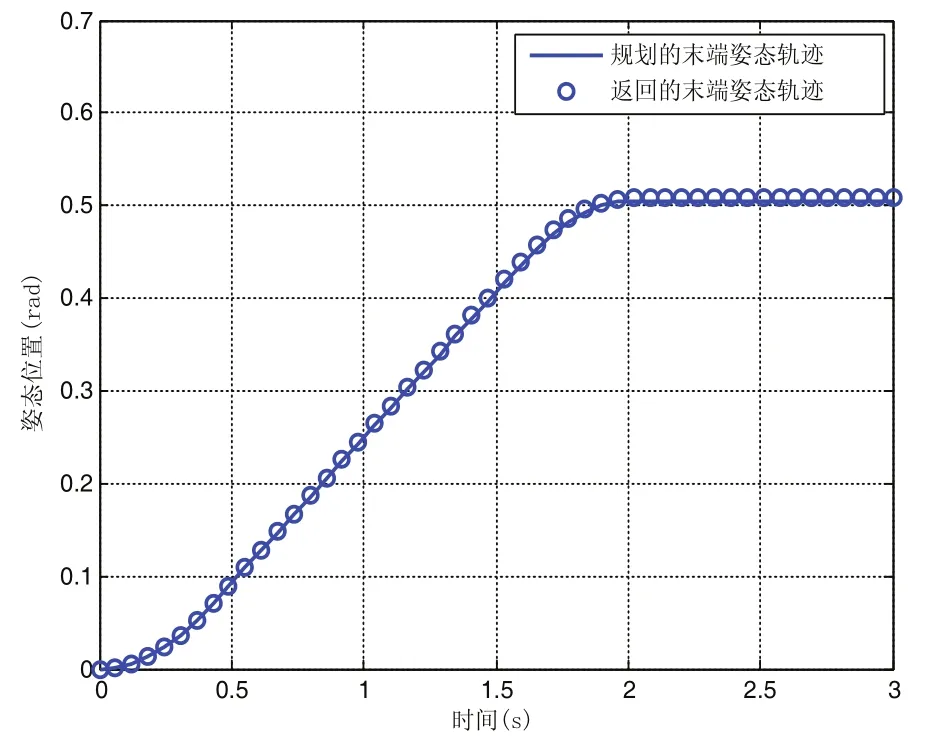
图6　规划末端姿态角度和实际姿态角度

综合关节空间和任务空间的仿真结果，验证了基于牛顿欧拉方法的线性解耦控制方案的有效性，实现了机器人良好的跟踪性能和稳定性能。

4　结论

首先通过ADAMS建立起六自由度串联机器人模型，然后在Simulink上搭建机器人的控制框图，最后利用ADAMS和MATLAB两款软件进行联合仿真，观察机器人的运行过程。通过对比规划的路径和机器人实际运行的路径曲线，可发现线性解耦控制方法能够快速、准确的控制机器人运动。

［1］ 王芳.机器人控制算法及其仿真系统的研究与实现［D］.上海:华东师范大学，2008.

［2］ 黎育红，聂凌霄.基于ADAMS虚拟样机的多体系统动力学仿真［J］.武汉大学学报（工学版），2010，43（6）:758-761.

［3］ 胡蕴博.基于ADAMS和MATLAB的机器人联合运动仿真［J］.机电技术，2015，4（2）:23-27.

［4］ 马如奇，郝双晖，郑伟峰，郝明晖，宋宝玉.基于MATLAB与ADAMS的机械臂联合仿真研究［J］.机械设计与制造，2010（4）: 93-95.

［5］ 李月月.基于ADAMS和MATLAB的机器人联合仿真［D］.河北:河北大学，2010.

［6］ 应再恩，平雪良，陈鲁刚.基于ADAMS和MATLAB的双回路PID控制倒立摆联合仿真［J］.机械传动，2012，36（8）:64-67.

［7］ 王战中，杨长建，刘超颖，熊蒙.基于MATLAB和ADAMS的六自由度机器人联合仿真［J］.制造业自动化，2013:30-33.

［8］ 龚建球，刘守斌.基于Adams和Matlab的自平衡机器人仿真［J］.机电工程，2008，25（2）:8-10，73.

［9］ 张建政，刘伟，高峰.6-PSS并联机器人动力学模型的牛顿-欧拉方法［J］.机械设计与研究，2007，23（3）:54-57，69.

［10］ Khalil W，Dombre E. Modeling， Identification and Control of Robots［M］.Taylor & Francis，Inc.2002.

The research on coordinated simulation of decoupling control for industrial robots

WANG kun1，2，LIANG Yan-yang1，2，LIU Hong-wei2

TP319

A

1009-0134（2016）09-0072-03

2016-07-07

四川省科技厅科技支撑项目（2014NZ118）；四川省教育厅项目（15ZB120）

汪坤（1991 -），男，湖北广水人，硕士，研究方向为机器人运行学和动力学建模与分析，机器人运动控制技术。