LM算法求解大残差非线性最小二乘问题研究
祝 强,李少康,徐 臻
(1.西安工业大学测试与控制技术研究所,陕西 西安 710021;2.西安共达精密机器有限公司,陕西 西安 710075)
LM算法求解大残差非线性最小二乘问题研究
祝强1,李少康1,徐臻2
(1.西安工业大学测试与控制技术研究所,陕西 西安 710021;2.西安共达精密机器有限公司,陕西 西安 710075)
针对传统LM算法求解大残差非线性最小二乘问题时存在算法失效的现象,分析Hessian矩阵与其近似矩阵的相似度对LM算法有效性的影响,提出一种依据残差变化方向搜索信赖域区间的自寻优LM算法。优化阻尼系数的更新算法,引入大残差引起的局部不收敛判断条件,以最速下降法结束当前迭代。迭代过程均以目标函数值的减小作为接受条件,算法稳定可靠。圆拟合测试结果证明:自寻优LM算法对待求参数初始值的选取不敏感,在15°夹角短圆弧、大残差等极端条件下仍可获得较快的收敛速度和良好拟合效果。自寻优LM算法具有较强的鲁棒性和稳定性,性能明显优于传统LM算法。
LM算法;高斯牛顿法;最小二乘;残差
0 引 言
在工程应用中,许多问题都可以归结为非线性最小二乘问题的最优化实现,如圆拟合、非线性型面拟合。目前,大多数非线性最优化方法是把目标函数按Taylor级数进行展开,舍去高阶项,将非线性目标函数近似线性化,通过迭代算法求解待求参数,使其不断逼近最优目标。
常用算法有最速下降法、Newton法[1-2]、Gauss-Newton(GN)法、Levenberg-Marquardt(LM)算法等。最速下降法利用负梯度方向作为搜索方向,是一种非常稳定的算法,但收敛速度不能尽如人意。Newton法保留了目标函数Taylor级数展开式中的一阶项和二阶项,具有二次收敛速度,但每一步迭代都需要计算Hessian矩阵,计算繁琐。GN法以目标函数的Jacobian矩阵来构造Hessian矩阵的近似矩阵H′,提高了算法效率。以上两者具有相同的缺陷,若Hessian矩阵或其近似矩阵H′为奇异矩阵时,两种算法都无法继续迭代。
LM算法[3-4]属于一种信赖域算法,由学者K. Levenberg以及D.Marquardt研究提出的,目的在于解决Hessian构造矩阵的非正定问题和奇异问题。LM算法主要用于求解非线性多元目标函数[5]的最优问题,目前对LM算法的研究主要集中在收敛速率和稳定性上,如利用外在曲率在传统LM算法中加入辅助加速项[6-7]来提高LM算法的收敛速度。采用Sobolev梯度替代欧氏梯度[8-9]实现LM算法求解非线性最小二乘问题。通过分析和改进阻尼系数的更新策略[10-11],使LM算法具有更强的适用性等。本文旨在分析残差水平与算法稳定性之间的关系,特别是求解非线性最小二乘问题,待求参数初始值的选取对LM算法稳定性和收敛速度的影响,对阻尼系数和信赖域的更新策略进行改进,使之具有更强的稳定性。
1 LM算法推导及分析
1.1LM算法
以误差平方和SSE构造最小二乘目标函数[5-6]F(x,w),表示为

式中:x——输入参数向量;
w——待求参数向量;
N——待求参数向量的个数;
f——目标函数单项残差值;
M——离散非线性系统的采样点个数。
令k为迭代步数,wk、wk+1分别为第k步、第k+1步迭代搜索到的待求参数值,待求参数取wk时,Jacobian矩阵表示为Jk,单项残差值表示为fk,梯度向量表示为gk,Hessian矩阵表示为Hk,则Newton法迭代公式为
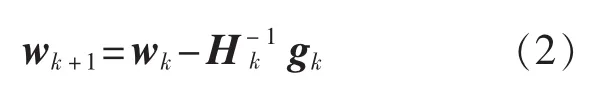

式(3)说明Newton算法以负梯度方向作为极小值的搜索方向,相比于最速下降法而言,其步长不再通过线性精确搜索获得,而是采用Hessian矩阵的逆矩阵作为搜索步长,算法具有二次收敛速度。当矩阵H为奇异矩阵时,无法求得其逆矩阵,Newton法无法进行迭代。同时,Hessian矩阵的正定性是Newton法搜索方向正确的保证。
GN法的迭代公式为
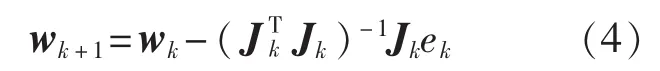
GN法以Jacobian矩阵来计算Hessian矩阵的近似矩阵,迭代过程中不再计算目标函数的二阶偏导,算法效率得以提高。但两者具有同样的缺陷,当近似Hessian矩阵奇异或非正定时,算法无法执行或发散。
为了克服Newton法和GN法存在的缺陷,LM算法采用新的方法构造近似Hessian矩阵,保证算法的稳定性。LM算法迭代公式为

从迭代公式可以得出,LM算法是最速下降法和GN法的组合。阻尼系数μ相当于权值,当μ=0时,LM算法蜕化为GN法;当系数μ较大时,LM算法近似为最速下降法。系数μ的选择保证了LM算法的有效性,避免近似Hessian矩阵不可逆情况的出现。LM算法的实现方式不是唯一的[7-8],研究的主要内容集中在矩阵H的构造方法以及阻尼系数μ的更新公式上,但各种算法都是以学者D.Marquardt给出的LM算法为基础,这里称之为传统LM算法。
1.2传统LM算法在圆拟合中的应用分析
圆拟合[12-13]属于非线性最小二乘问题,是工程应用中经常遇到的一种曲线拟合[14-15],如回转零件加工和测量中的坐标系建立、圆度测量等。圆拟合通常是在被测工件或装置上对其某一截面进行采样,获取该截圆上的离散采样点,通过优化算法进行圆拟合计算,得到圆心和半径信息。
在理论半径为100mm,采样点数为11个,误差水平±2μm条件下,采用传统LM算法对不同采样点中心夹角、不同初始值情况下进行拟合计算,分析残差、夹角对算法带来的影响。设定最大迭代次数为50次,当梯度向量的二范数或待求参数向量增量的二范数<10-6时,迭代终止,仿真测试在Matlab中完成,测试结果如表1所示。表中“夹角”是指采样点所含中心夹角大小,“初始值”是指算法选择的待求参数初始向量,对于圆拟合,待求参数向量为(x,y,r),即圆心坐标和半径。“拟合圆心”是指算法得到的圆心坐标(x,y)。传统LM算法的圆拟合结果可以得出,当采样点中心夹角较大、待求参数初始值接近理论值时,算法可以获得较为理想的拟合结果。如夹角为90°、120°,初始值选取为[0,2,90]或[-2,2,60]时,传统LM算法得到的拟合圆信息较为真实,拟合圆心及拟合半径偏差符合圆拟合中叠加误差与采样夹角间的误差传递关系。当初始值远离理论值时,如[-20,20,10],算法不能收敛,无法得到正确的圆信息。
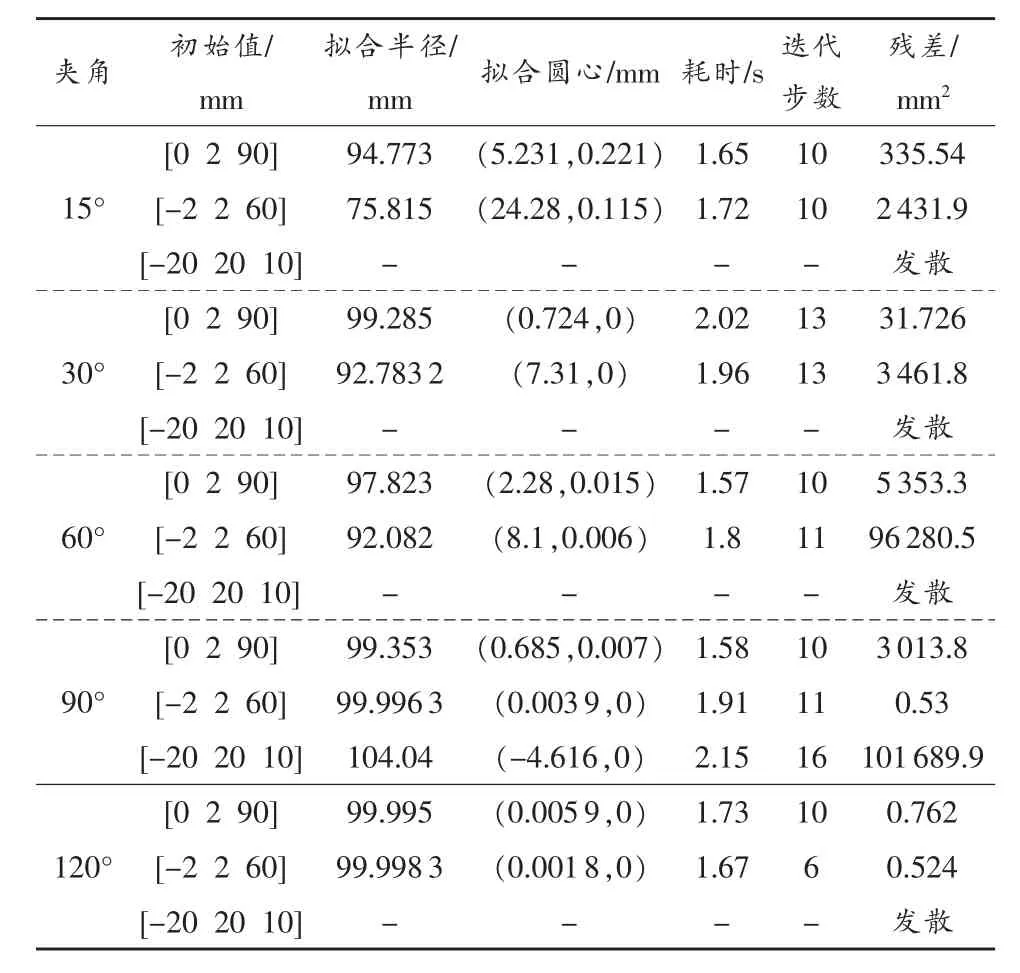
表1 传统LM算法的圆拟合结果
从传统LM算法推导过程分析,算法采用Jacobian矩阵来计算Hessian矩阵的近似矩阵,在流程中以增益系数λ的符号来判断当前迭代点是否可以接受。也就是说,如果λ>0,算法认为当前迭代点保证了目标函数的下降趋势,并以增益系数λ来计算下一步迭代的阻尼系数μ。对残差函数f(x+h)按Taylor级数展开,并忽略二阶及以上项,可得:

目标函数可近似表示为
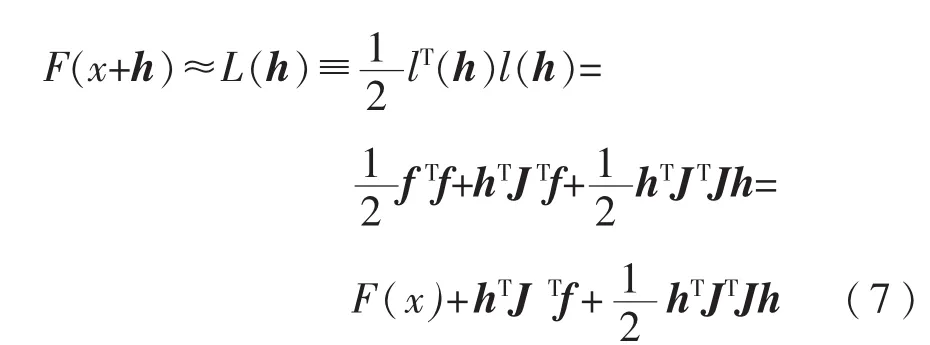
传统LM算法中增益系数λ的计算如下式:
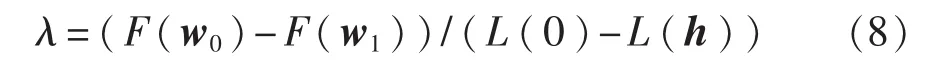
式(8)中分母项为

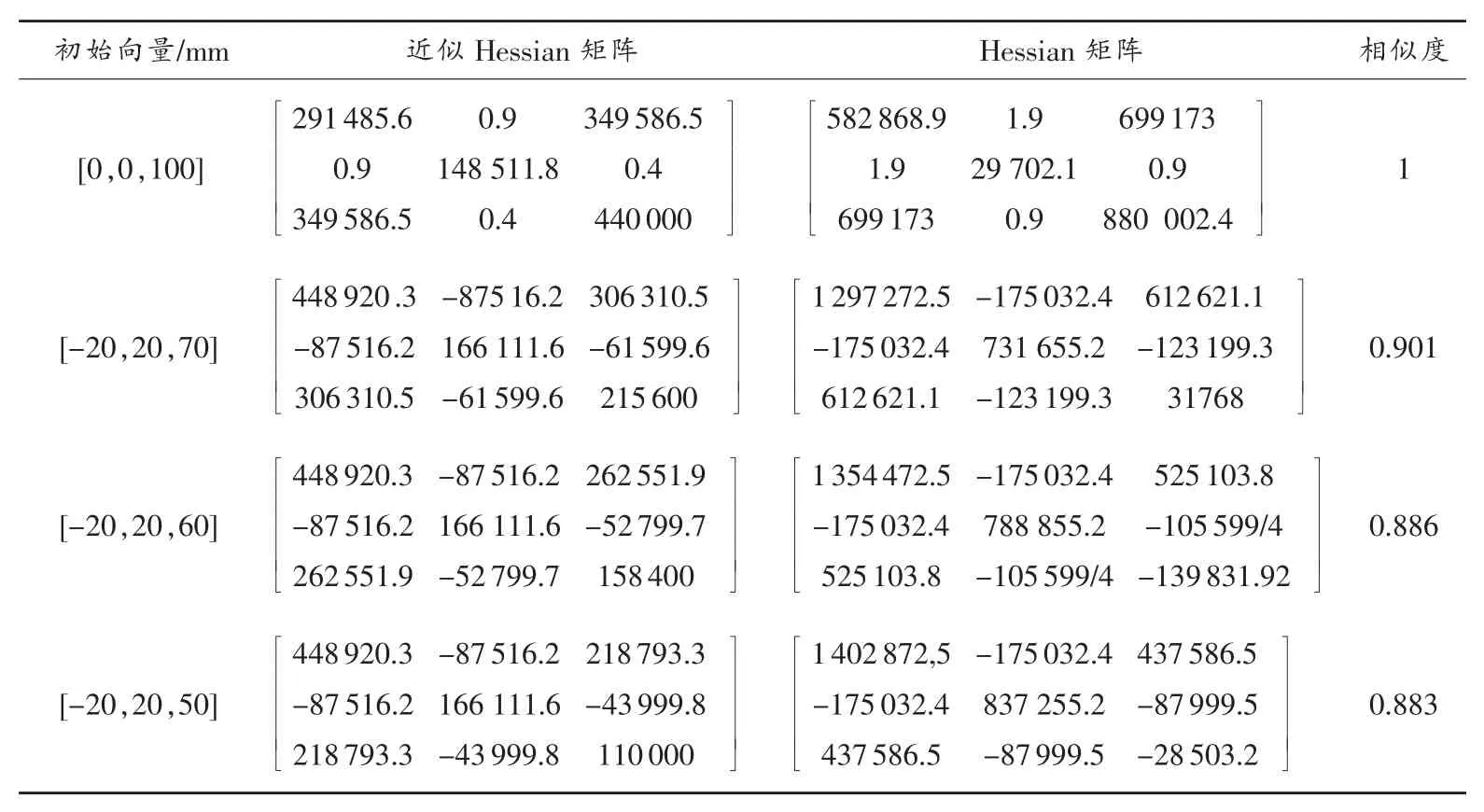
表2 初始向量选择对Hessian矩阵及近似Hessian矩阵的影响
由于阻尼系数μ>0,且hTh、-hTg为正,因此式(8)中的分母项必为正,这就是传统LM算法采用增益系数λ的符号来判断目标函数是否下降的原因。从上述推导过程可知,式(6)是该结论的基础。但在实际应用中,由于待求参数向量的理论值无法预知,选定的初始值可能远离理论值,从而导致采用线性模型来近似原目标函数不成立。在这种情况下,增益系数λ算式的分母项无法保证一定为正,传统LM算法中对残差变化方向的判断和阻尼系数μ的预测都会失效。
Pi在孤独而绝望的漂流中,选择了信仰上帝,“信仰上帝就是敞开心胸,就是不受拘束,就是深深的信任,就是爱的自由行动”有时候他会疲惫、愤怒、和忧伤,他就会努力让自己高兴起来。他会摸着用衬衫碎片做的包头巾大声说:“这是上帝的帽子”;他会指着理查德·帕克大声说“这是上帝的猫”;他会指着救生艇大声说“这是上帝的方舟”;他会摊开双手大声说“这是上帝的宽广土地”;他会指着天空大声说“这是上帝的耳朵”就这样,他一直提醒自己上帝的创造和自己在其中的位置。黑暗最终会消散,上帝会留下来,成为他心里一个闪光的点,他会继续去爱,并因为对这世界的爱而活下去。
为了分析初始值偏离理论值的程度对传统LM算法的影响,表2选取4种初始值向量,计算圆拟合目标函数对应的Hessian矩阵及其近似矩阵H(由Jacobian矩阵获得),并给出两者之间的相似度。表中理论圆圆心为(0,0),理论半径为100mm。由相似度结果可知,当初始向量为[0,0,100](向量元素依次为初始圆心坐标x、y,初始半径r),即不含偏差时,两者相似度为1。随着初始值不断偏离理论值,两者之间的相似度不断下降。
相似度变化表明传统LM算法不适合解决大残差条件下的非线性最小二乘问题,残差较大时将导致目标函数的线性近似产生严重偏离,导致算法对残差变化趋势判断出错,造成阻尼系数μ的预测失败,算法失稳。残差较大时:1)计算目标函数的二阶导数,LM算法蜕变为高斯牛顿法;2)改进阻尼系数的更新方法,提高LM算法的稳定性,在保持超线性收敛速度的同时,简化算法的计算复杂度。
2 自寻优LM算法
通过以上分析和测试可知,当残差较大时,传统LM算法可能失效,算法无法获得正确的圆拟合结果。针对这种情况,本文提出一种改进的自寻优LM算法,修正信赖域搜索条件,优化阻尼系数的更新方式,使LM算法具有更强鲁棒性。算法流程如下:
1)初始化各变量,迭代步数k=0,确定待求参数向量初始值w0,设定迭代停止条件ε,最大迭代步数kmax。
2)计算Hessian近似矩阵H,H=JTkJk,计算梯度向量g,g=Jkfk。
3)第1步采用最速下降法计算下降方向h,采用一维准确线性搜索计算步长d,得到搜索点w1,w1=w0-d·h。迭代步数k=k+1,更新搜索点,w0=w1,计算H、g。
5)计算待求参数变化量h,h=-H-1g,更新搜索点w1=w0-h,计算目标函数值F1,令λmin=λ0,λ0=λ0+2λa,λmax=λ0,转至6)。
6)如果F1≤F0,更新搜索点,w0=w1。迭代步数k= k+1,若k>kmax,转至11)。否则,转至4);如果F1>F0,令Fmin=F1,转至7)。
7)更新阻尼系数μ=(λmin+λmax)/2,Fold=F1,更新矩阵,计算待求参数变化量h,更新搜索点w′=w0-h,计算目标函数值F1。
8)如果 Fmin>F1,置 Fmin=F1,λmin=λ0,num=0;否则,num=num+1;若num>10,置ρ=1,转9);否则,转至10)。
9)采用最速下降法替代本步迭代过程,计算迭代搜索点w1,w1=w0-d·h,更新搜索点,w0=w1,转至4)。
10)如果Fold≤F1,搜索方向残差增大,令λmax=λ0,λ0=λ0+λa/5,λmin=λ0,l=0,ν=2。如果Fold>F1,搜索方向残差减小,若l=1,令ν=2ν。更新变量λmin=λ0,λ0=λ0+ ν×λa,λmax=λ0,l=1。跳转至6)。
11)结束迭代。
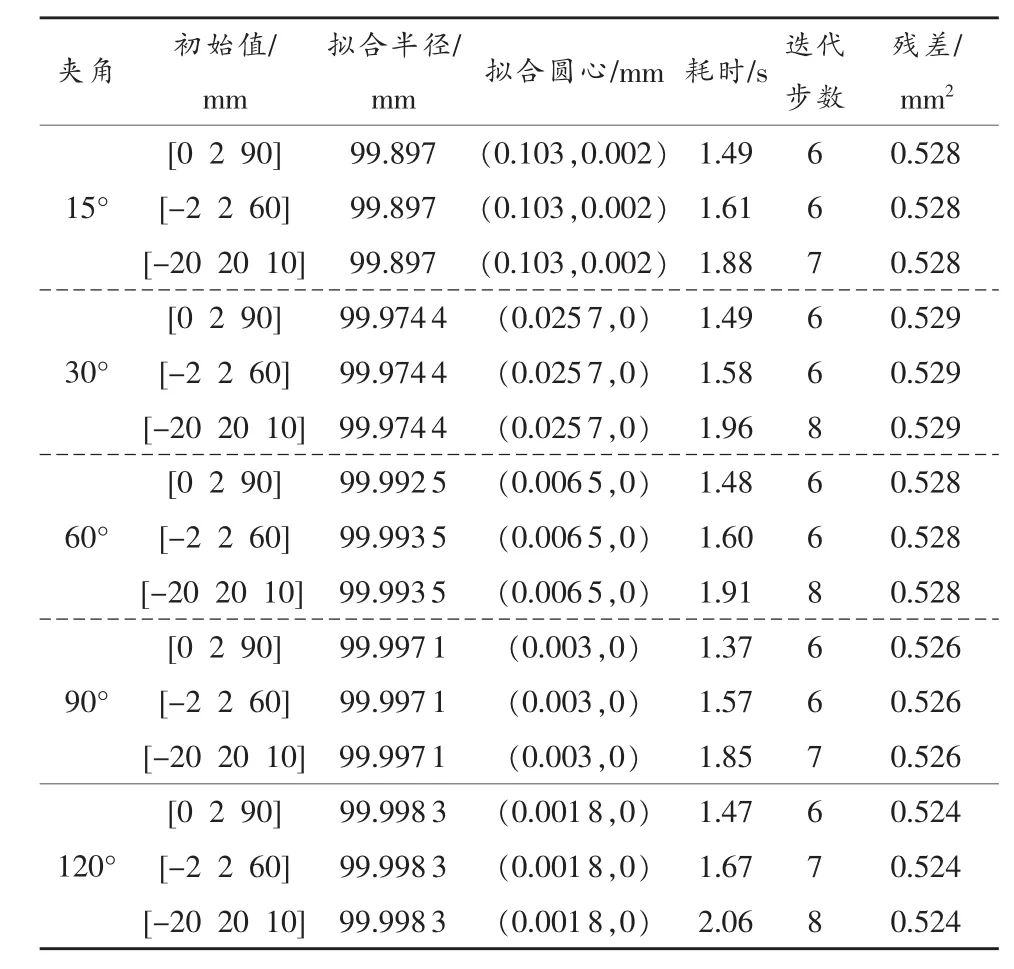
表3 自寻优LM算法的圆拟合结果
自寻优LM算法的每一步迭代过程均以目标函数值减小作为接受条件,确保残差保持下降趋势。阻尼系数μ的更新不再依赖于目标函数值的变化,而是在搜索过程中根据残差变化方向进行修正,自动调整搜索范围λmin、λmax,实现合理阻尼系数的快速搜索,避免了大残差条件下产生错误的搜索方向。由于实际采样点总会带有一定的误差,当误差水平较高时,残差会出现连续增大情况,表示无法很快找到合理的阻尼系数或当前搜索方向错误,阻尼系数的搜索耗时过长,算法将停止本次搜索,而改用最速下降法来计算本次迭代过程,保证算法的正常进行。
3 自寻优LM算法测试分析
为了测试自寻优LM算法在大残差情况下的运行状态,以表1中的测试条件进行仿真,对5种不同中心夹角和3种不同初始值情况下进行圆拟合计算,仿真结果如表3所示。
从表中测试结果来看,自寻优LM算法的稳定性明显优于传统LM算法,在初始值远离理论值时仍然获得了理想的圆拟合结果。当采样点分布于中心夹角15°极端条件下,算法的拟合结果正确且稳定。从各种拟合条件下的测试结果来看,自寻优LM算法的迭代步数和计算时间基本恒定,目标函数的最终残差值接近一致,即算法效率不受采样条件和初始值选择的影响,具有很强的鲁棒性。
4 结束语
本文以圆拟合为例,分析了初始值选择对Hessian矩阵及近似矩阵之间相似度的影响,证明了传统LM算法不适合解决大残差条件下的非线性最小二乘问题,从理论层面给出传统LM算法失效的原因。文中提出自寻优LM算法,算法修正了寻找最优信赖域的条件,优化了阻尼系数的计算方法,提高LM算法的鲁棒性。圆拟合仿真测试证明,自寻优LM算法的稳定性明显优于传统LM算法,算法效率不受初值的影响,在短圆弧、初值远离理论值时均可获得良好的拟合结果。
[1]WANG X H,LI C.Convergence of newton’s method and uniqueness of the solution of equations in banach space II[J].Acta Mathematica Sinica,2003,19(2):405-412.
[2]PROINOV P D.General local convergence theory for a class of iterative processes and its applications to newton’s method[J].Journal of Complexity,2009,25(1):38-62.
[3]MARQUARDT D W.An algorithm for the least-squares estimation of nonlinear parameters[J].Journal of the Society for Industrial and Applied Mathematics,1963,11(2):431-441.
[4]LEVENBERG K.A method for the solution of certain non-linearproblemsinleastsquares[J].Quarterly Journal of Applied Mathmatics,1944,2(2):164-168.
[5]魏荣,卢俊国,王执铨.基于Levenberg-Marquardt算法和最小二乘方法的小波网络混合学习算法[J].信息与控制,2001,30(5):440-442.
[6]TRANSTRUM M K,MACHTA B B,SETHNA J P, Why are nonlinear fits to data so challenging[J].Phys Rev Lett,2010(104):060201.
[7]TRANSTRUMA M K,SETHNA J P.Improvements to the Levenberg-Marquardt algorithm for nonlinear leastsquares minimization[J].Journal of Computational Physics,2012,11(1):1-32.
[8]RENKARJ.Nonlinearleastsquaresand Sobolev gradients[J].AppliedNumerical Mathematics,2013(65):91-104.
[9]KAZEMIP,RENKARJ.ALevenberg-Marquardt method based on sobolev gradients[J].Nonlinear Analy sis:Theory,Methods&Applications,2012,75(16):6170-6179.
[10]LAMPTON M.Damping-undamping strategies for the Levenberg-Marquardt nonlinear Least-Squares method[J]. Computers in Physics Journal,1997,11(1):110-115.
[11]张鸿燕,耿征.Levenberg-Marquardt算法的一种新解释[J].计算机工程与应用,2009,45(3):5-8.
[12]UMBACH D,JONES K N.A few methods for fitting circlestodata[J].IEEE Trans on Instrumentation and Measurement,2003,52(6):1181-1885.
[13]KANATANI K,SUGAYA Y.Performance evaluation of iterative geometric fitting algorithms[J].Computational Statistics&Data Analysis,2007,52(2):1208-1222.
[14]ALSHARADQAH A,CHERNOV N.Error analysis for circle fitting algorithms[J].Electronic Journal of Statistics,2009,21(3):886-911.
[15]CHERNOV N,LESORT C.Statistical efficiency of curve fitting algorithms[J].Computational Statistics and Data Analysis,2004,47(4):713-728.
(编辑:莫婕)
Study of solving nonlinear least squares under large residual based on Levenberg-Marquardt algorithm
ZHU Qiang1,LI Shaokang1,XU Zhen2
(1.Institute of Measurement and Control Technology,Xi’an Technological University,Xi’an 710021,China;2.Xi’an GongDa Precision Machine Co.,Ltd.,Xi’an 710075,China)
The traditional Levenberg-Marquardt algorithm(LM algorithm)is always invalid in solving large residual nonlinear least squares problems.Thus,how the similarity between Hessian matrix and its approximate matrix influences the effectiveness of the traditional LM algorithm is analyzed.And a self-optimizing LM algorithm that the residual changing direction is used to search for trust-region intervals is proposed.The updating algorithm of damping coefficient is improved;A judging condition is introduced to solve the localdivergence caused by large residual;and the LM algorithm is substituted by the steepest descent method.It is the unique accepting condition that the objective function value is decreased continuously in the iterative process.The self-optimizing LM algorithm is stable and reliable.Circle fitting tests show that the self-optimizing LM algorithm is insensitive to the initial value of searching parameters.Under the extremeconditionssuchaslargeresidualandtheshortarcof15°includedangle,the convergence is fast and the fitting results are good,which proves that this new algorithm is robust and stable and its performance is superior to the traditional LM algorithm.
Levenberg-Marquardt algorithm;Gauss-Newton algorithm;least squares;residual
A
1674-5124(2016)03-0012-05
10.11857/j.issn.1674-5124.2016.03.003
2015-07-30;
2015-09-11
国家自然科学基金(51475351);陕西省科学技术研究发展计划项目(2013K08-12);陕西省协同创新计划项目(2015XT-32);西安工业大学校长基金(XAGDXJJ1006)
祝强(1972-),男,湖北襄阳市人,副教授,博士,研究方向为精密测量与控制技术。

