基于LSSVM的污水处理过程建模
王 欣,宋翼颉,秦 斌,彭小玉
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
基于LSSVM的污水处理过程建模
王欣,宋翼颉,秦斌,彭小玉
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
针对基准仿真1号模型(BSM1)有耗时久、结构复杂、不利于研究和优化等缺点,提出使用多输入多输出最小二乘支持向量机(LSSVM)对污水处理过程进行建模。先介绍BSM1,再在BSM1的基础上建立基于LSSVM的污水处理过程简化模型,最后将BSM1的仿真结果与基于LSSVM的污水处理模型的仿真结果进行比较,验证得出基于LSSVM的污水处理过程模型运行效率更高。
最小二乘支持向量机;污水处理过程;基准仿真1号模型
0 引言
在大力推进生态文明建设的大背景下,切实加大水污染防治的力度十分必要,污水处理的研究也应运而生。目前,污水生物处理的所有反应过程都可以在一个单纯的活性污泥系统内完成。由于微生物系统间存在着相互作用,描述这些过程的数学模型较复杂[1]。在污水处理过程综合模型研究的初期阶段,研究人员不得不从事大量的计算,并最大限度地从数学模型中寻求答案。国际水污染控制与研究协会提出了活性污泥1号模型,该模型为污水处理过程模型的深入研究奠定了基础,同时也衍生出了许多其它污水处理过程模型[2]。国际水质协会(International Association on Water Quality,IAWQ)和欧盟科学技术委员会(Committee on Science and Technology,COST)开发了基准仿真1号模型(benchmark simulation model no.1,BSM1),该模型成为了活性污泥废水处理过程控制方案的一个评估工具[3]。但是BSM1在许多场合的工作效率低下,因此本文提出基于最小二乘支持向量机(least squares support vector machine,LSSVM)的污水处理过程简化模型,并进行仿真验证。为了提高仿真结果的可接受性,在MATLAB/SIMULINK环境中分别建立了BSM1和基于LSSVM的污水处理过程简化模型,并把两者的仿真结果进行对比分析。
1 在MATLAB/SIMULINK中搭建BSM1
BSM1分为2个部分,其设备布局如图1所示。
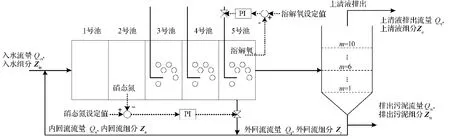
图1 BSM1设备布局Fig. 1 BSM1 layout
图1中各个流量的单位均为m3/d,各个组分为污水中13种物质的质量浓度组成的向量,单位均为mg/L[4]。BSM1有2个部分:一部分是基于BSM1的5个生化反应池模型,其中包括2个缺氧生化反应池模型和3个好氧反应池模型;另一部分是沉淀池模型,沉淀池模型使用了Tak cs的双指数沉淀速度模型来描述沉淀池的运作情况[5]。
BSM1中所有的微分方程、化学计量数和动力学参数在国际水质协会(IAWQ)的网站[6]上均可查到。在仔细阅读J. B. Copp等编写的编程仿真手册后即可以在MATLAB中建立起BSM1[5]。BSM1的仿真过程就是解一个包含145个微分方程的方程组。为了使模型更容易理解和更具有可操作性,选择在SIMULINK环境下搭建BSM1。考虑到求解速度,BSM1中的生化反应池和沉淀池模块均使用S函数编写。
在国际水质协会的网站上,可以找到干燥天气、少雨天气和暴雨天气的入水流量和组分的数据。同时,为了方便用户对搭建起来的模型进行验证,还提供了这145个微分方程的初值以及在开环状态下第一天出水总悬浮颗粒质量浓度的变化曲线,如图2所示。

图2 国际水质协会所提供的出水总悬浮颗粒质量浓度曲线Fig. 2 The mass concentration curve of total suspended particles provided by IAWQ
搭建好BSM1后,使用干燥天气的入水数据,在开环情况下进行仿真,可以得到出水总悬浮颗粒质量浓度的变化曲线,如图3所示。

图3 BSM1开环仿真的出水总悬浮颗粒质量浓度曲线Fig. 3 The mass concentration curve of total suspended particles made by BSM1 in open loop
由图2 和图3可以看出,搭建起来的BSM1的开环仿真结果与国际水质协会所提供的结果完全一致,可进行下一步研究。
污水处理过程中最重要的就是生物脱氮部分。生物脱氮分为2个部分,硝化反应和反硝化反应。硝化反应在好氧区进行,反硝化反应在缺氧区进行。为了使硝化反应能够充分进行,好氧区的溶解氧就成了一个比较重要的变量。因此,国际水质协会提出了如下控制策略,采用PI控制器控制5号池的氧转移系数,从而使5号池中的溶解氧质量浓度达到稳定;同时采用PI控制器控制混合液回流量,从而使2号池出水的硝态氮质量浓度达到稳定。根据这一控制策略,可以在SIMULINK环境中搭建出如图4所示闭环状态下的BSM1。图中Q0为流入1号池的流量,Qi为第i号池的出水流量(i=1, 2, …, 5),ki为i号池的氧转移系数(i=1, 2, …, 5),Qf为流入二沉池的流量,为外回流流量的给定值,为排出污泥流量的给定值,为2号池硝态氮质量浓度的给定值,为5号池溶解氧质量浓度的给定值,为延迟因子。
将仿真时间设定为[0, 14],可以得到2号池出水的硝态氮质量浓度(2(NO))的变化曲线如图5所示,5号池中的溶解氧质量浓度(5(O2))的变化曲线如图6所示。

图4 在SIMULINK环境中搭建的BSM1Fig. 4 BSM1 model in SIMULINK

图5 BSM1闭环仿真2(NO)的变化曲线Fig. 5 The simulated2(NO) curve of BSM1 in closed loop

图6 BSM1闭环模型仿真5(O2)的变化曲线Fig. 6 The simulated5(O2) curve of BSM1 in closed loop
由图5和图6可知,2号池出水的硝态氮质量浓度在较快达到稳定后,大致稳定在0到1.3之间,波动较大,这说明2号池出水的硝态氮质量浓度的控制器还有较大的优化空间。5号池的溶解氧质量浓度有比较大的超调量,但是很快达到了稳定状态,稳态误差基本为0。
2 基于MIMO-LSSVM的污水处理过程简化模型
2.1最小二乘支持向量机
统计学习理论解决了传统统计学中的一些难题,例如“过学习”和“欠学习”的问题[7]。支持向量机(support verctor machine,SVM)是由Vapnik等在统计学习理论的基础上,建立的一种机器学习方法。支持向量机在分类和回归上有比较广泛的应用,但是支持向量机的解法存在耗时的二次规划问题,因此又发展出了最小二乘支持向量机(least square support vector machine,LSSVM)[7-8]。下面介绍最小二乘支持向量机回归的数学理论。
LSSVM在求解过程中用等式代替了SVM中的不等式,从而避免了求解二次规划问题。因此LSSVM在求解速度上比SVM具有更大的优势。LSSVM对回归问题的描述为给定样本集:

式中:xi为输入向量数据样本;
yi为输出数据样本;
d为输入向量的维度;
l为样本个数。
最小二乘支持向量机的回归函数形式为

f(x)为待确定的映射关系;
w为权重向量;
wT为w的转置向量;
b为偏置量。
最小二乘支持向量机的求解就是求解w和b,这样就可以使用结构风险最小化原则来描述LSSVM的求解:

式中:ei为第i个样本的预测误差;
C为正则化参数,C的取值可以用来在泛化能力和模型训练误差之间进行折中。
因此,可以构建出拉格朗日函数:

从式(3)可以看出,LSSVM的求解最终化为一个线性方程组的求解。正是因为最后不需要再象SVM那样去解二次规划问题,所以LSSVM在求解时效率更高。
2.2简化模型的结构
BSM1中有2个控制量和2个被控量,这2个被控量同时还影响着出水水质。由于BSM1中的参数较多、数学模型较复杂,所以在预测、优化等场合,BSM1的运行效率较低。
因此,本研究提出建立基于LSSVM的污水处理过程模型。以2号池出水硝态氮质量浓度(2(NO))和5号池出水的溶解氧质量浓度(5(O2))作为输出,5号池氧转移系数和混合液回流量为输入,以入水流量和入水中各种物质质量浓度作为扰动,建立污水处理过程简化模型。由于BSM1中的微分方程均为一阶,且没有延迟环节,所以在建立简化模型时可以认为当前输出与上一时刻的输出2(NO)(k-1)和5(O2)(k-1)相关。这样简化模型的输入还需要加入上一采样时刻的2号池硝态氮质量浓度2(NO)(k-1),上一采样时刻的5号池溶解氧质量浓度5(O2)(k-1),简化模型的结构如图7所示。
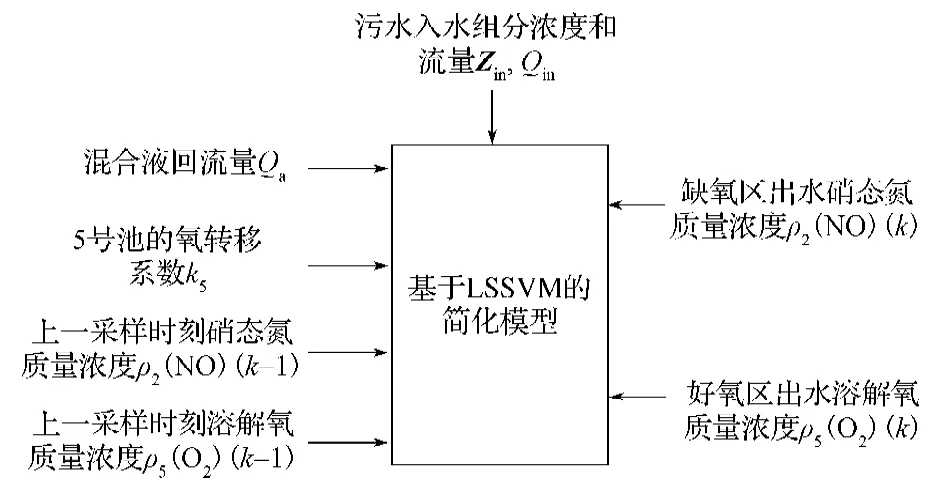
图7 基于LSSVM的污水处理过程模型的结构Fig. 7 The model structure for LSSVM-based sewage treatment
2.3简化模型的仿真
将BSM1 14 d的开环仿真结果作为数据样本,开环输入为参数在各自区间上的均匀分布的随机数,采样时间定为3 min,这样采样结果将有6 721组数据。将其中75%的数据作为训练样本,25%的数据作为测试样本。对于同样的数据样本,标准支持向量机和最小二乘支持向量机对测试样本的预测能力如表1所示。从表中可以看出,标准支持向量机对测试样本的预测误差比最小二乘支持向量机的预测误差要高很多。

表1 SVM和LSSVM对测试样本的预测误差对比Table 1 Prediction error comparison of SVM and LSSVM on test samples
将仿真时间设为[0, 2],入水数据为干燥天气的数据,BSM1和基于LSSVM的污水处理过程模型各自的运行时间对比如表2所示。

表2 BSM1和基于LSSVM的模型的运行时间对比Table 2 The runtime comparison of BSM1 and the model based on LSSVM
最后,为了验证模型,将基于LSSVM的污水处理过程模型在SIMULINK环境下仿真,仿真时间设为[0, 14],使用干燥天气的入水数据,仿真结果如图8~11中虚线所示。从图8和图9可以看出,硝态氮质量浓度的预测曲线基本与BSM1的曲线保持一致。从图10可以看出,溶解氧质量浓度的预测曲线在稳定状态下能够和BSM1的曲线保持一致;但是从图11可以看出,溶解氧的预测曲线在超调部分未能有较好的预测效果。

图8 2(NO)的变化曲线对比Fig. 8 The2(NO) curve comparison

图9 放大的2(NO)对比图Fig. 9 The amplifed2(NO) curve comparison
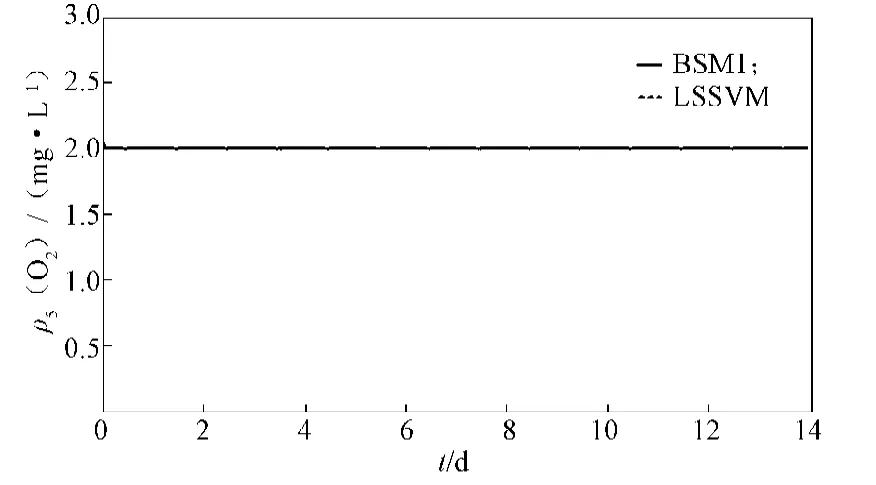
图10 5(O2)的变化曲线对比Fig. 10 The5(O2) curve comparison

图11 放大的5(O2)对比图Fig. 11 The amplifed5(O2) curve comparison
3 结语
基于机理模型运行速度慢的缺点,本文提出在BSM1的基础上建立基于LSSVM的简化模型,这种简化模型忽略了机理模型中大量不需要关心的中间变量和参数,改善了机理模型结构复杂、耗时长、中间变量多的缺点。研究人员只需要找出所关心的变量的数据对模型进行训练,即可获得一个预测精准的黑箱模型。从仿真结果可以看出,基于LSSVM的污水处理过程模型可以在和BSM1的结果保持一致的基础上,运行速度比BSM1更快。
[1]顾夏声. 废水生物处理数学模式[M]. 2版. 北京: 清华大学出版社,1993:123-124. GU Xiasheng. Sewage Treatment Mathematical Model[M]. 2nd ed. Beijing:Tsinghua University Press,1993:123-124.
[2]余颖,乔俊飞. 活性污泥法污水处理过程的建模与仿真技术的研究[J]. 信息与控制,2004,33(6):709-713,728. YU Ying,QIAO Junfei. Modeling and Simulation Technology of Activated Sludge Method on Wastewater Treatment Process[J]. Information and Control,2004,33(6):709-713,728.
[3]黄明智. 废水处理系统水质特征动态分析的混合智能控制研究[D]. 广州:华南理工大学,2010. HUANG Mingzhi. Study on Hybrid Intelligent Control for Water Quality Dynamic Parameters in Wastewater Treatment System[D]. Guangzhou:South China University of Technology,2010.
[4]黄晓琪. 污水处理过程节能优化控制方法的研究[D]. 北京:北京工业大学,2013. HUANG Xiaoqi. Research on Energy-Saving Optimal Control Method for Wastewater Treatment Process[D]. Beijing:Beijing University of Technology,2013.
[5]刘大伟,沈文浩. 用Matlab/Simulink建立废水处理仿真模型[J]. 环境科学与技术,2007,30(11):86-89. LIU Dawei,SHEN Wenhao. Set Up BSM1 with Matlab/ Simulink[J]. Environmental Science and Technology,2007,30(11):86-89.
[6]COPP J B. Description of BSM1[EB/OL]. [2014-11-17]. http://www.benchmarkwwtp.org/.
[7]程萍. 基于最小二乘支持向量机的非线性广义预测控制[D]. 太原:太原理工大学,2010. CHENG Ping. Generalized Predictive Control Algorithm Based on Least Squares Support Vector Machines[D]. Taiyuan:Taiyuan University of Technology,2010.
[8]郭振凯,宋召青,毛剑琴. 基于最小二乘支持向量机的非线性广义预测控制[J]. 控制与决策,2009,24(4):520-525,531. GUO Zhenkai,SONG Zhaoqing,MAO Jianqin. Nonlinear Generalized Predictive Control Based on Least Squaresupport Vector Machine[J]. Control and Decision,2009,24(4):520-525,531.
(责任编辑:邓光辉)
Modeling of Sewage Treatment Process Based on MIMO-LSSVM
WANG Xin,SONG Yijie,QIN Bin,PENG Xiaoyu
(School of Electric and Information Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
In view of shortcomings of Benchmark simulation model no.1 (BSM1) , such as time consuming, complicated structure and hard to research and optimization, a model based on LSSVM (least squares support vector machine) for sewage treatment process is presented. Introduces BSM1 firstly, then establishes LSSVM-based simplified model of sewage treatment process on BSM1, finally compares the simulation results of BSM1 and LSSVM-based model. It indicates that the LSSVM-based model has higher operation efficiency.
least squares support vector machine;sewage treatment process;benchmark simulation model no.1
TP15
A
1673-9833(2016)01-0059-05
10.3969/j.issn.1673-9833.2016.01.011
2015-11-03
王欣(1971-),女,湖南株洲人,湖南工业大学教授,博士,主要研究方向为复杂过程建模,机器学习,E-mail:1114084900@qq.com
宋翼颉(1991-),男,湖南长沙人,湖南工业大学硕士生,主要研究方向为复杂过程建模控制与优化,E-mail:6569107@qq.com

