随机共振液压泵故障特征信号提取

经　哲，郭　利

（军械工程学院导弹工程系，河北 石家庄 050003）

随机共振液压泵故障特征信号提取

经哲，郭利

（军械工程学院导弹工程系，河北 石家庄 050003）

针对强噪声背景下的液压泵故障特征提取问题，提出一种自适应级联单势阱随机共振的特征提取方法。首先验证广义相关系数可作为自适应随机共振优化算法的目标函数，然后采用量子遗传算法优化单势阱随机共振系统的结构参数，再将所得的自适应单势阱随机共振系统进行级联。该方法只需调节每一级随机共振的一个系统结构参数，优化速度快，且采用级联方式能更准确地提取液压泵故障信号的低频成分。数值仿真分析表明：该方法可有效地提取淹没在强噪声背景下的多频信号；实际测试结果证明其能有效地检测液压泵故障信号的特征频率，为液压泵故障预测和诊断奠定基础。

单势阱随机共振；级联；广义相关系数；量子遗传算法；液压泵故障特征信号

0　引　言

液压泵是液压系统最核心的组成部分之一，直接决定着整个液压系统能否正常运行。然而液压泵结构复杂、工作压力大，又需连续运行，很容易发生故障或影响其他零部件的正常运行。因此，对液压泵性能的早期监测，提前发生故障征兆具有重要意义。液压泵的基频及其谐波频率是轴向柱塞泵松靴、滑靴等故障的特征频率，准确提取强噪声背景下的基频及其谐波频率对液压泵的故障诊断具有重要意义［1］。

随机共振（stochastic resonance，SR）的提出改变了一直以来人们对噪声的不良印象，且已广泛应用于机械振动的故障提取和诊断［2-3］，尤其是在微弱信号检测方面，引起学者的兴趣。经典的随机共振常为双稳系统［4］，因此需要通过调节系统结构参数a和b来改变势垒［5-6］，从而使系统达到最佳共振状态，使得随机共振在工程实际中的应用更加广泛［7-8］。但在对强噪声背景下的液压泵故障特征信号检测时，采用双稳随机共振系统，存在优化两个参数的计算量较大、耗费时间较长且很难在一定范围内使两个参数同时达到最优等问题。而单势阱随机共振（single-well potential SR，SPSR）没有势垒，仅由一个稳态点组成，因此，只需调节参数b即可［9］，在简化随机共振优化的同时，适用于多频周期微弱信号的检测［10］。

级联随机共振（cascaded SR，CSR）系统利用级联的方式，进行多次共振降噪，已广泛应用于轴承［11］、机械［12］故障诊断，在时域波形检测上具有去高频毛刺和突出波形轮廓的特点［13］；在频域内，可以使高频能量不断向低频能量转移，从而实现滤除高频成分和提取低频成分［14］。

本文针对强噪声背景下的液压泵故障特征提取问题，提出一种自适应级联单势阱随机共振（adaptive cascaded single-well potential SR，ACSPSR）的特征提取方法。该种方法在优化过程中选取广义相关系数为目标函数，避免了信噪比不适用于多频信号检测的缺陷［15］。且每一级SR只需调节一个系统结构参数，计算量小，优化速度快。同时采用级联的方式，能更准确地提取液压泵故障信号的低频成分。

1　随机共振

1.1单势阱随机共振

随机共振由周期信号和噪声共同作用产生，可用朗之万方程（Langevin equation，LE）将这种双稳系统表示如下：

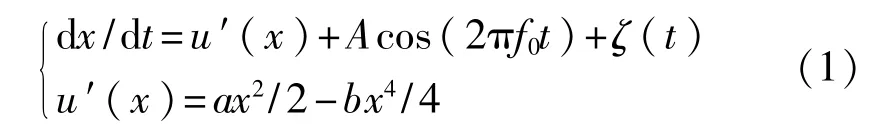
式中：u＇（x）——系统的势函数；

a、b——大于0的实数；

Acos（2πf0t）——驱动信号，振幅为A，频率为f0；

ζ（t）——强度为D、均值为零的高斯白噪声，

且有＜ζ（t），ζ（0）＞=2Dδ（t）。

单势阱随机共振的势函数为：u（x）=a-bx2/2，则u＇（x）=bx，系统中不含有参数a。随机共振的单双势阱如图1所示。

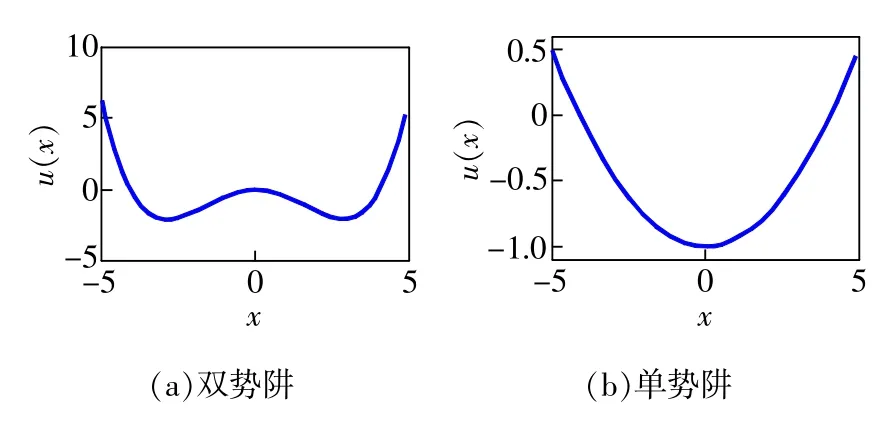
图1　随机共振的势阱

传统的随机共振有两个势阱点，当存在外加周期力时，势函数受到调制，随机共振发生时，信号从噪声中吸收能量，从一个势阱跃迁到另一个势阱，从而增加输出信噪比。而单势阱系统没有势垒，随机共振发生时，信号在获取噪声能量的同时，沿着势阱的边缘运动，同样会提高信号的信噪比［16］。

1.2级联随机共振

对随机共振进行级联，使其进行处理传递，将上一级SR的系统输出作为下一级SR的输入，其结构如图2所示。

图2　级联随机共振系统

以两层随机共振模型为例，级联系统可表示为

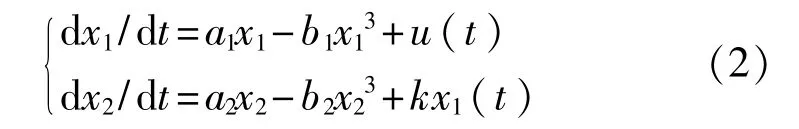
2　以广义相关系数为目标函数的自适应级联单势阱随机共振

2.1广义相关系数的性质

基于互信息的广义相关系数（general correlation function，GCF）是判定变量间广义相关程度的一种指标，可表示为

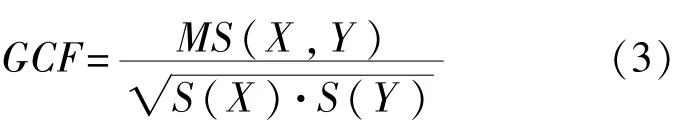
式中：MS（X，Y）——随机变量X与Y的互信息熵；

S（X）、S（Y）——X与Y的信息熵。

广义相关系数满足非负性、独立性和对称性，因此可以用来度量信号去噪前后的差异程度。以仿真信号为例，设输入的信号为sig（t）=0.3sin（2π×0.01t）+ n（t），采样频率fs=5Hz，n（t）是噪声强度为1.5的高斯白噪声。设噪声为零时系统的信噪比为零，随机共振的系统结构参数为a=1，b=1，则经随机共振处理后的信号的广义相关系数随噪声强度的变化趋势如图3所示。

图3　输出信号的广义相关系数与噪声强度的关系

由图可知，随噪声强度的增加，广义相关系数呈先增后减的趋势，这说明，在噪声强度很小时，随着噪声强度的增加，信号、噪声和系统发生协同作用，广义相关系数增加，系统性能得到改善；在广义相关系数取得最大值时，系统达到最佳共振状态；随后，噪声的强度继续增大，此时噪声的增加只会导致信噪比的下降，恶化系统性能，因此广义相关系数随噪声的强度增加而减小，且随机共振现象逐渐消失。综上所述，广义相关系数可以衡量随机共振是否发生，因此可作为自适应随机共振优化的适应度函数。

2.2自适应级联单势阱随机共振

将单势阱的势函数代入级联随机共振系统，则方程组可改写为

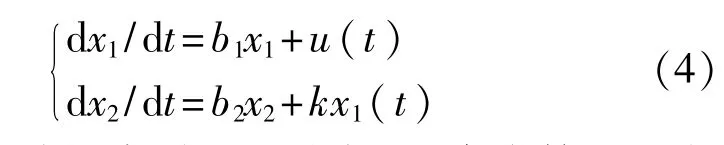
经典随机共振常采用四阶龙格-库塔算法对方程组进行求解［17］，则级联单势阱随机共振每一级的迭代方程如下：

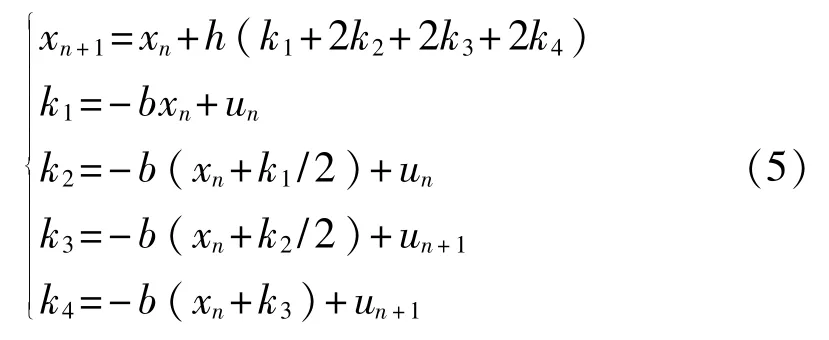
式中：un——输入信号；

x——系统的输出信号；

h——步长。

量子遗传算法（quantum genetic algorithm，QGA）是一种将量子计算原理和遗传算法相结合的随机搜索优化算法。QGA与GA相比，保持了较好的种群多样性，且具有良好的全局搜索能力。

以广义相关系数为自适应度函数的基于量子遗传算法的自适应级联单势阱随机共振算法流程如图4所示。

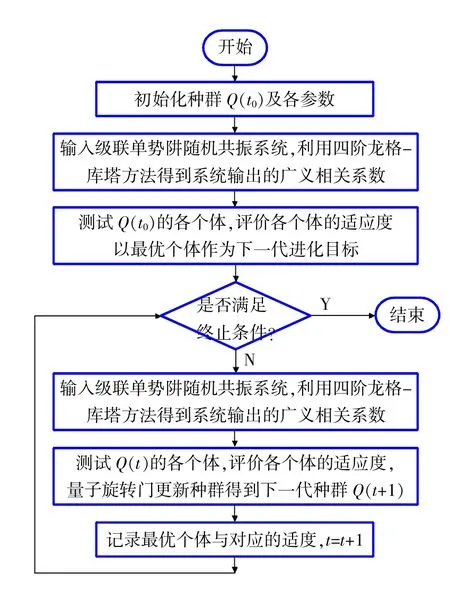
图4　自适应随机共振流程图

3　数值仿真分析

设随机共振的输入信号为

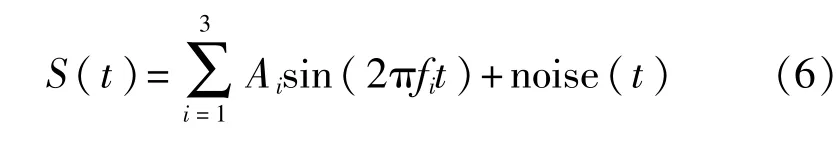
其中A1=A2=A3=0.01，f1=10 Hz，f2=30 Hz，f3=60 Hz，noise（t）是噪声强度为1.5的高斯白噪声。

信号的采样频率为fs=2kHz，采样点数为N=8192。级联随机共振中k的取值较大［18］，本文仅取k=50。利用四阶龙格-库塔对随机共振方程进行求解，步长为h=1/fs，为保证随机共振求解过程中的收敛性，参数a和h应满足［16］ah≤1，因此CSR系统参数a和b的取值范围为［0.01 5］和［0.01 10］，CSR以及ACSPSR中b的取值范围为［0.01 10］。设量子遗传算法的最大进化代数为300，种群大小为100，传统随机共振因遵守绝热近似理论，故只能检测频率远小于1 Hz的信号，但工程实际应用中，频率常常远大于1 Hz，故采用变尺度随机共振方法［19］先对采集到的信号进行线性压缩，利用QGA对随机共振系统参数进行优化，并对信号进行处理，最后按压缩尺度还原实测数据。本文设置的压缩倍数为250，优化结果及时间如表1所示。

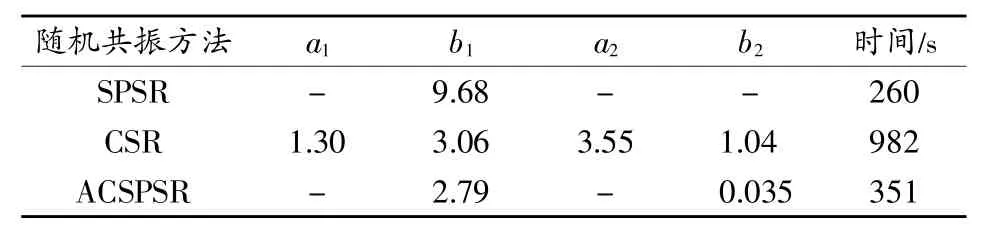
表1　不同随机共振的优化结果

由表可知，CSR需要优化的参数最多，且时间最长。将优化后的参数分别代入相应的随机共振系统，得到的输入信号时域图和频谱图分别如图5、图6所示。

由图5可知，SPSR的时域去噪效果并不明显，经CSR处理的输出信号时域中周期性较明显，而经过ACSPSR处理后的信号大致体现出了波形的部分特征。由图6可以看出，SPSR可以提取信号的多频成分，但是频谱谱值较低，去噪效果一般；CSR虽然也可以提取信号的多频成分，但是在0～30 Hz之间有许多频率成分干扰了对信号频率成分的判断，这与理论分析中CSR可滤除高频成分相吻合。ACSPSR的频谱图中，信号的3个频率成分明显，且幅值较大，效果最好。

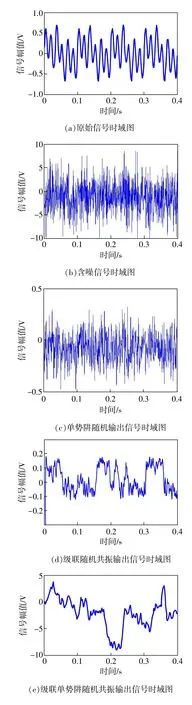
图5　时域波形

4　工程应用

在液压泵的常见故障模式中，滑靴松动是目前最容易发生的故障之一。当发生松靴故障时，柱塞球头会对滑靴产生强烈的冲击，进而滑靴将这种冲击传给斜盘，导致壳体产生振动，振动的高频能量通过共振的形式传递，导致液压泵端盖处非固有的振动信号能量增强，称之为附加冲击振动。该附加冲击振动为判断液压泵是否发生松靴故障提供重要的信息。本文采用试验器件名称及型号如表2所示。

表2　试验器件名称及型号

其中，驱动电机的额定转速为1480r/min；液压泵的柱塞数为7，理论排量为10 mL/r，额定转速为1500r/min，液压泵主溢流阀压力为10MPa，采样频率为20kHz，采样点数为10000。由于泵轴的转速为1500r/min，单个柱塞附加冲击的基频为f=n/60（n为电机的转速），则本试验的液压泵的冲击振动基频为1480/60×7=172.667Hz。

采集信号的时域波形和包络谱如图7所示。

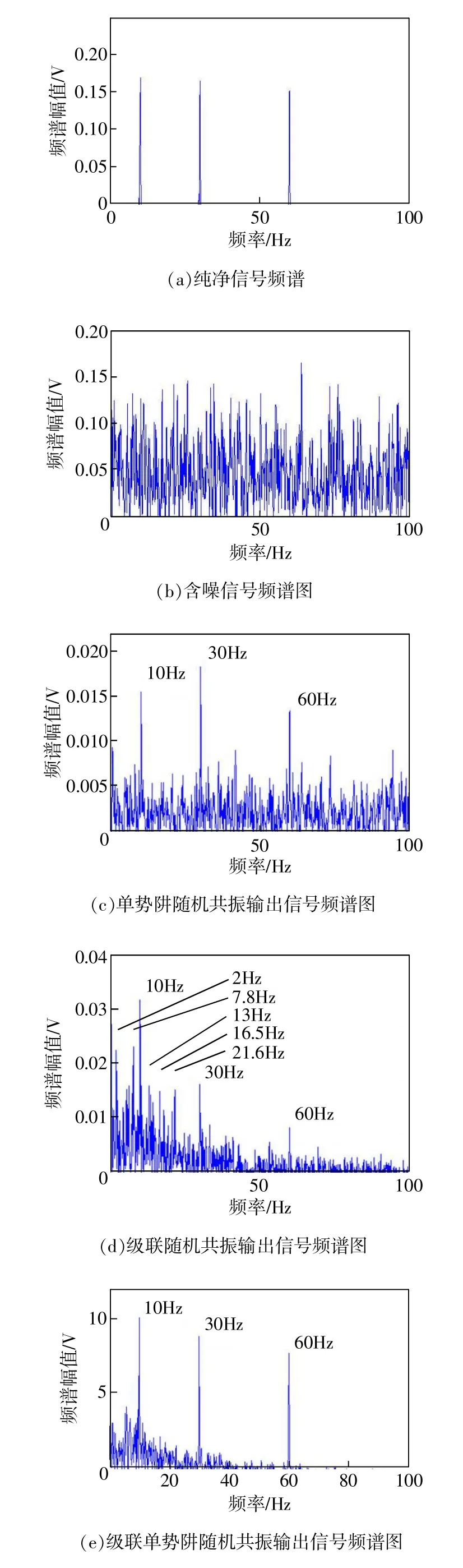
图6　频谱图

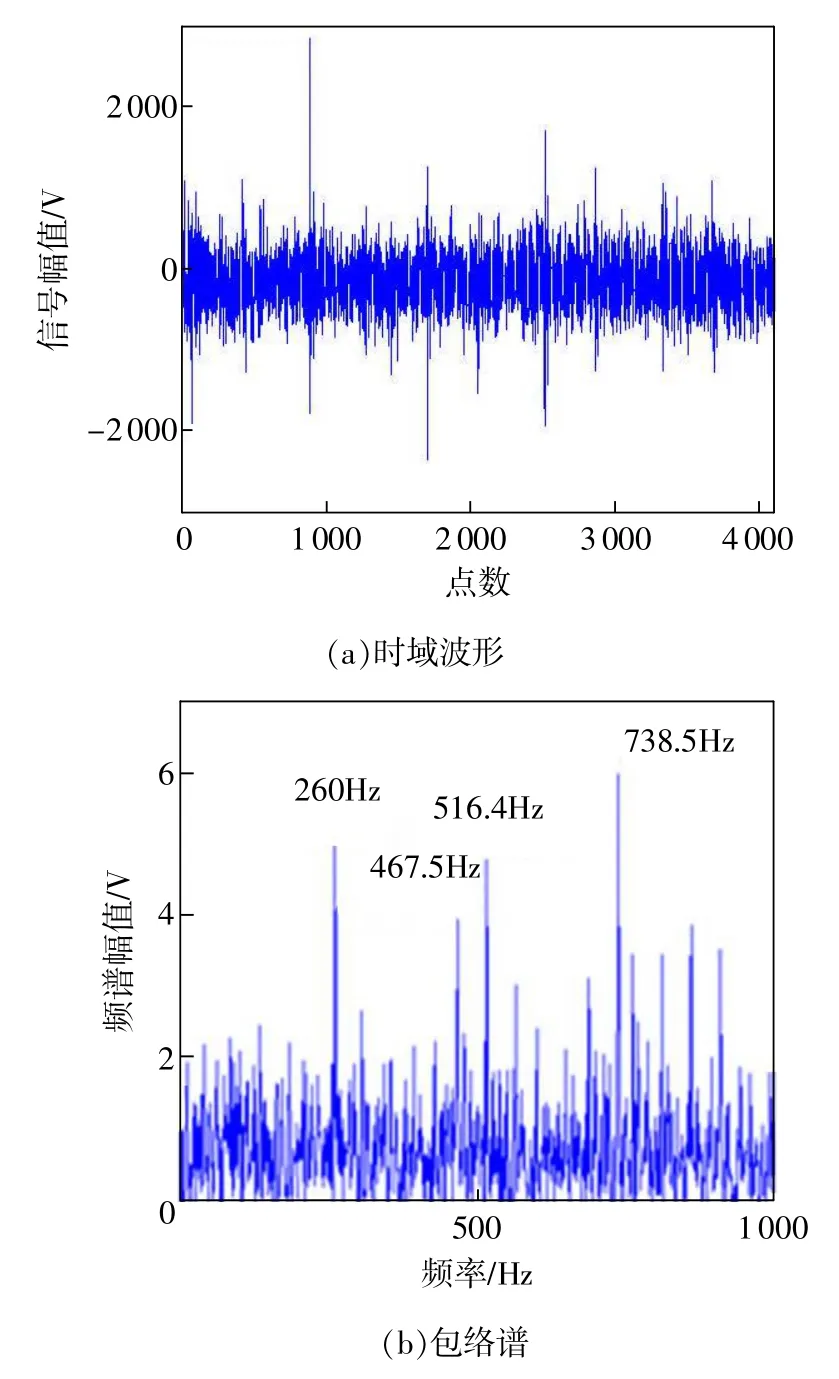
图7　松靴状态下信号的时域波形和包络谱

利用QGA优化随机共振参数，得b1=3.56，b2= 0.098，将优化结果代入本文所提的方法，输出信号的时域波形和包络谱如图8所示。

对比可知，未经随机共振处理的原始信号中，时域只能分辨冲击成分，在频域中原始信号的能量集中在260 Hz等处，故障特征频率172.667Hz及其二倍频处的谱峰被噪声所淹没，因此很难对故障进行识别。利用本文所提方法对信号进行处理后，时域中，冲击信号之间呈现出明显的周期性。在包络谱图中不但能分辨液压泵的故障特征频率及其二倍频，而且172.667 Hz的谐波簇也清晰可见，与理论分析结果一致。因此本文所提方法能够将液压泵信号的基频及倍频有效提取出来，是强噪声背景下提取多频微弱信号的一种有效方法，适用于实际工程应用。

5　结束语

本文提出一种基于级联单势阱的自适应随机共振方法，并通过仿真和工程实测信号验证了所提方法的有效性。通过研究，得出以下结论：

图8　经级联单势阱随机共振处理后信号的时域波形和包络谱

1）通过对广义相关系数的分析，证明以广义相关系数为目标函数优化随机共振，能够达到较好的效果。

2）级联单势阱随机共振结合了级联随机共振良好的频率压缩效果和单势阱随机共振能有效提取多频信号、优化参数较少的特点，能够有效地提取信号中的多频成分。

3）仿真信号结果表明，本文提出的方法优于以往的单势阱随机共振和级联随机共振等传统方法，液压泵微弱故障特征信号分析表明，本文提出的方法更适用于工程实际。

［1］李扬.形态学滤波新方法及其在旋转机械故障诊断中的应用［D］.河北：燕山大学，2013.

［2］任立通，胡金海，谢寿生，等.基于随机共振预处理的振动故障特征提取研究［J］.振动与冲击，2014，33（2）：141-146.

［3］冷永刚，田祥友.一阶线性系统随机共振在转子轴故障诊断中的应用研究［J］.振动与冲击，2014，33（17）：1-5.

［4］TWETEN D J，MANN B P.Experimental investigation of colored noise in stochastic resonance of a bistable beam［J］.Physica D，2014（268）：25-33.

［5］张仲海，王多，王太勇，等.采用粒子群算法的自适应变步长随机共振研究［J］.振动与冲击，2013，32（19）：125-130.

［6］WEI F，LV M，WANG G，et al.Research on multifrequencyweaksignaldetectionbasedonadaptive flexiblestochasticresonance［J］.AdvancedMaterials Research Vols，2015（1079-1080）：757-761.

［7］WEIF，LV M，WANG G，et al.Research on multifrequencyweaksignaldetectionbasedonadaptive flexiblestochasticresonance［J］.AdavancedMaterials Research Vols，2015（1070-1080）：757-761.

［8］XU B H，DUAN F B，BAO R H，et al.Stochastic resonance with tuning system parameters：the application ofbistable systems in signal processing［J］.Chaos，Solitons and Fractals，2002（13）：633-644.

［9］ZHANG W，XIANG B R.A new single-well potential stochastic resonance algorithm to detect the weak signal［J］. Talanta，2006（70）：267-271.

［10］陶志颖，鲁昌华，查正兴，等.基于单势阱随机共振的多频周期微弱信号检测［J］.电子测量与仪器学报，2014，28（2）：171-176.

［11］赵军，崔颖，刘维，等.基于随机共振和BBS/ICA的轴承故障诊断［J］.北京工业大学学报，2014，40（2）：176-181.

［12］郝研，王太勇，万剑，等.基于级联双稳随机共振和多重分形的机械故障诊断方法研究［J］.振动与冲击，2012，31（8）：181-185.

［13］冷永刚，王太勇，郭焱，等.级联双稳系统的随机共振特性［J］.物理学报，2005，54（3）：1118-1125.

［14］何慧龙，王太勇，冷永刚，等.级联双稳随机共振系统非线性滤波特性［J］.吉林大学学报（工学版），2007，37（4）：905-909.

［15］王曦.基于随机共振的弱信号检测研究［D］.北京：北京邮电大学，2010.

［16］蒋世奇，古天祥.随机振幅周期信号驱动的一阶线性系统的随机共振［J］.电子测量与仪器学报，2008，22（1）：104-108.

［17］胡茑庆.随机共振微弱特征信号检测理论与方法 ［M］.北京：国防工业出版社，2012.

［18］谢磊.轴承振动分析与寿命评估方法研究［D］.成都：电子科技大学，2013.

［19］范胜波，王太勇，冷永刚，等.基于变尺度随机共振的弱周期性冲击信号的检测［J］.中国机械工程，2006，17（4）：387-390.

（编辑：刘杨）

Research on feature extraction of hydraulic pump vibration signals based on stochastic resonance

JING Zhe，GUO Li
（Department of Missile Engineering，Ordnance Engineering College，Shijiazhuang 050003，China）

An adaptive cascaded single-potential well stochastic resonance method（ACSPSR）has been proposed to extract hydraulic pump fault characteristics in strong noise backgrounds.This paper first verified that general correlation function could be used as the fitness function of stochastic resonance optimization algorithm and then used quantum genetic algorithm（QGA）to optimize the parameters of single-potential well stochastic resonance（SPSR）.The last step was to cascade the SPSR.The proposed method only requires the optimization of a systematic structural parameter at each cascade of stochastic resonance.The speed of optimization is fast and by using the cascaded stochastic resonance，the low-frequency components of hydraulic pump fault signals can be more accurately extracted.Simulation data indicates that the method can effectively extract multi-frequency signals in strong noise backgrounds.Practical test results show that the ACSPSR can effectively detect the characteristic frequency of hydraulic pump fault signals，thus laying a good foundation for pump fault prediction and diagnosis.

single-well potential stochastic resonance；cascaded；general correlation function；quantum genetic algorithm；hydraulic pump fault characteristic signal

A

1674-5124（2016）05-0107-06

10.11857/j.issn.1674-5124.2016.05.023

2015-10-10；

2015-12-29

国家自然科学基金项目（51275524）

经哲（1989-），女，内蒙古乌兰浩特市人，硕士，专业方向为装备状态监测和故障预测。