Theory on Structure and Coloring of Maximal Planar Graphs (4)-Operations and Kempe Equivalent Classes

XU Jin



Theory on Structure and Coloring of Maximal Planar Graphs (4)-Operations and Kempe Equivalent Classes

XU Jin*

(,,100871,),(,,100871,)

Letbe a-chromatic graph.is called a Kempe graph if all-colorings ofare Kempe equivalent. It is an unsolved and hard problem to characterize the properties of Kempe graphs with chromatic number. The Kempe equivalence of maximal planar graphs is addressed in this paper. Our contributions are as follows: (1) Observe and study a class of subgraphs, called 2-chromatic ears, which play a critical role in guaranteeing the Kempe equivalence between two 4-colorings; (2) Introduce and explore the properties of-characteristic graphs, which clearly characterize the relations of all 4-colorings of a graph; (3) Divide the Kempe equivalent classes of non-Kempe 4-chromatic maximal planar graphs into three classes, tree-type, cycle-type, and circular-cycle-type, and point out that all these three classes can exist simultaneously in the set of 4-colorings of one maximal planar graph; (4) Study the characteristics of Kempe maximal planar graphs, introduce a recursive domino method to construct such graphs, and propose two conjectures.

Kempe maximal planar graph; Kempe transformation;operation, Kempe equivalent class;characteristic graph; 2-chromatic ear

1 Introduction

The importance of planar graphs is reflected in two factors: mathematical theory and practical applications. At a theoretical level, there are many famous conjectures that have significant influences in graph theory and even in mathematics, such as the Four-Color Conjecture, the Uniquely Four- Colorable Planar Graph Conjecture, the Nine- Color Conjecture, and Three-colorable Problem.[1]. At a practical level, the planar graph theory can be directly applied to the fields of science such as circuit wiring[2]and information science[3].

Maximal planar graphs are an important subclass of planar graphs. Each face of a maximal planar graph is a triangle, so it is also called a triangulation. Since the researching objects of the Four-Color Conjecture can be confined to maximal planar graphs, numerous topics around maximal planar graphs have attracted the attentions and imaginations of researchers for more than a century, including degree sequences, constructions, coloring characters, traversability, and generating operations[4]. In the studying process of tackling Four-Color Conjecture, scholars proposed many conjectures, such as Uniquely Four-Colorable Planar Graph Conjecture and Nine-Color Conjecture, which gradually form the central research field on coloring theory of maximal planar graphs.

In terms of graph coloring theory, Kempe changes are proved to be one of the basic and most powerful tools. A Kempe change is to exchange two colors of a connected component of a 2-coloring induced subgraph, and remain the colors of the other vertices unchanged in a coloring graph. Thedefined in this paper is the operation that contains one or more Kempe changes under a 4-coloring (The specific definition is in Section 3). Ais in fact a coloring-derived operation, which can induce a 4-coloring from another 4-coloring of a graph

The Kempe changes are introduced by Kempe in his false proof of the four color theorem[5], after which Fisk first systematically studied this topic until 1977, showing that all 4-colorings of a maximal planar graphare Kempe equivalent ifhas no vertex with odd degree[6]. Subsequently, Meyniel[7], in 1978, showed that all 5-colorings of a planar graph are Kempe equivalent. In 1981, Vergnas and Meyniel proved: all 5-colorings of any simple graph not contractible toare Kempe equivalent[8]. In 2007, Mohar[9]proved that allof a planar graph with chromatic number less thanare Kempe equivalent, and proposed the following conjecture.

Conjecture 1[9]For, all-colorings of connectedgraphs that are not complete are Kempe equivalent.

In 2015, Feghali,.[10]have addressed the case whenby showing that all 3-colorings of a connected cubic graphare Kempe equivalent unlessis the complete graphor the triangular prism. Additionally, we1)prove that the conjecture is true when. Conjecture 1 is open for.

In 2008, Cereceda,.[11]studied thechromatic characteristic graphof a planar graph. The vertex set ofconsists of allof, and twoare joined by an edge inif they differ in color on just one vertex of. They proved that ifhas chromatic number, thenis not connected, on the other hand, forthere are graphs with chromatic numberfor whichis not connected, and there aregraphs for whichis connected.

Some scholars have also considered Kempe changes and Kempe equivalent classes on edge coloring, such as McDonald and Mohar[12], Sarah and Ruth[13],and so on.

The complexity of graph algorithms has been investigated based on Kempe changes and Kempe equivalent classes. The interested readers can refer to Refs. [14-24].

This series of articles aim to establish the coloring operation system of maximal planar graphs, which contains two coloring-derived operations, one is the, and the other is the(also called the pseudo-edge- induced coloring method, which will be introduced and researched in another paper). For a given maximal planar graph,are very likely not able to induce all 4-colorings (or some desired one) offrom a given 4-coloring, whilecan do well.

All graphs considered in this paper are finite, simple, and undirected. For a given graph, we use,andto denote the vertex set, the edge set, the degree of, and the neighborhood ofin(the set of all vertices adjacent to) respectively, written as,,andfor short if no confusion. The cardinality of the setis denoted as, called the order of. For a graph, if,, and two ends of each edge inbelong to, then we calla subgraph of. And in the subgraph, for,are adjacent in, if and only if they are also adjacent in, thenis called an induced subgraph ofinduced by, denoted by. The join of two disjoint graphsandis the result of joining each vertex ofwith every vertex of, denoted by.is a complete graph havingvertices. A wheel is the join of a cycleofvertices and a trivial graph, and denoted by, whereandare called the wheel-cycle and the wheel-center ofrespectively. Also, we write the wheel-cycleofas, where.

A graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends. Such a drawing is called a planar embedding of the graph. Any planar graph considered in the paper is assumed one of its planar embeddings. A maximal planar graph is a planar graph to which no new edges can be added without violating planarity. A triangulation is a planar graph in which every face is bounded by three edges (including its infinite face). It can be easily proved that maximal planar graphs are triangulations, and vice versa.

The graph shown in Fig. 1 is called a funnel,where the 1-degree vertex is the funnel top, the 3-degree vertex is the funnel middle, and the two 2-degree vertices are the funnel bottoms. If an induced subgraph of a graph is a funnel, then it is called a funnel subgraph of the graph. For more details about funnels, please refer to this series of articles (2)[25].

Fig. 1 The funnel

In this paper, we introduce the, and find that the inner mechanism that a new 4-coloring can be derived from a given 4-coloring byis closely related with a class of subgraphs, called 2-chromatic ears. Therefore, we make an in-depth research on 2-chromatic ears in Section 2. Section 3 introduces and explores the properties ofgraphs, which clearly characterize the relations of all 4-colorings of a graph. Section 4 discusses the limitations of, namely, some 4-colorings may not be able to be derived from a given 4-coloring by, based on which we partition the Kempe equivalent classes of non-Kempe graphs into three classes: tree-type, cycle-type, and circular-cycle-type. Section 5 studies the characteristics of Kempe graphs, introduces a recursive domino method to construct Kempe graphs, and proposes two conjectures to describe the properties of Kempe maximal planar graphs.

For more notations and terminologies, we refer the readers to Refs. [25-27].

2 2-Chromatic Ears

In this section, we first give the definition and classification of 2-chromatic cycles, and then we introduce the 2-chromatic ears, which is the root of implementingcontinuously.

2.1 Related definitions of 2-chromatic cycles

Fig. 2 Diagrams of the chord cycle, the chord-path cycle and the basic cycle

For a 4-colorable maximal planar graphunder a 4-coloring, and a given 2-chromatic cycleof, which type the 2-chromatic cyclebelongs to depends on the ways of planar embedding of. As the graph shown in Fig. 2(a), if its planar embedding is converted to the graph shown in Fig. 2(c), then the 2-chromatic cycleis a 2-chromatic chord-path cycle with a chord-pathwhileandare the 2- chromatic basic cycles. Unless special declaration, all 2-chromatic cycles in the following argument are 2-chromatic basic cycles. For a coloring, we denote bythe set of all 2-chromatic cycles under. A cycleofis 2-colorable if there exists a coloringsuch that. Useto denote the set of all 2-colorable cycles of. It is easy to show that

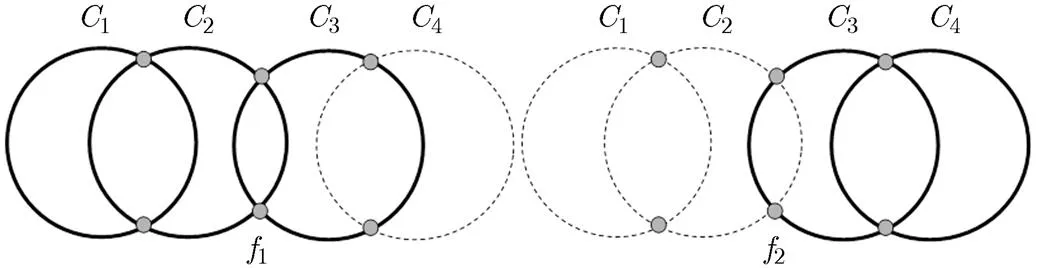
Fig. 3 An example of two relevant2-chromatic cycles

2.2 Related definitions and characteristics of 2- chromatic Ears

Fig. 4 The diagram of ears, co-root ears, and homologous ears

(2)The operation of interchanging the colors of all 34-components in the interior ofcan induce a new coloringsuch thatcontains a 2- chromatic cycledifferent fromif and only if

Proof (1) Suppose that there exist a cycleinor, which is consisted of only homochromatic ears. Then, by the definition of homochromatic ears, we have that any pair of ears ofnot only are homologous, but also have the same color set under. Therefore,is a 2- chromatic cycle of. This contradicts the assumption of.

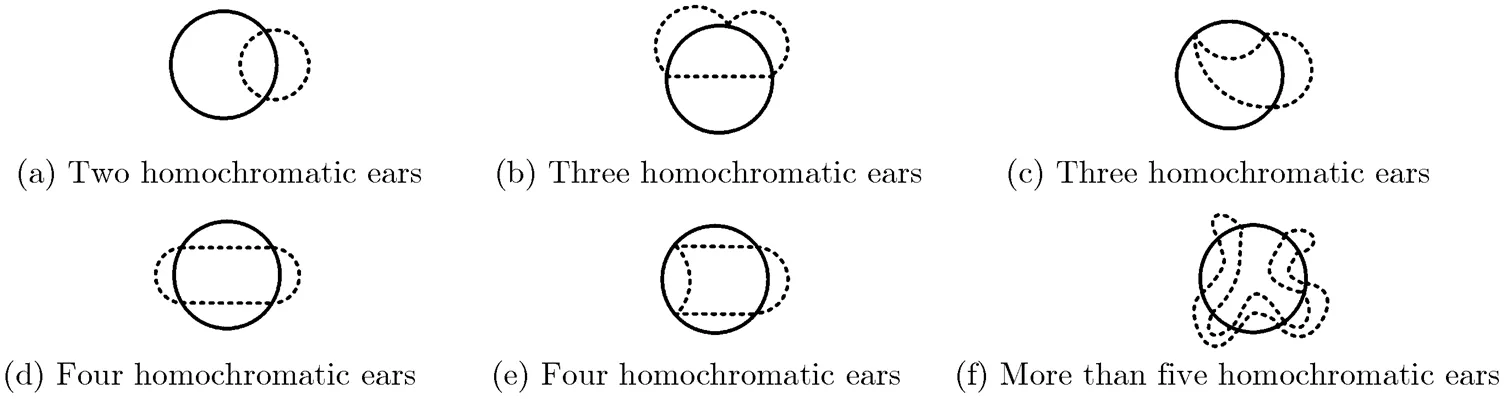
Fig. 5 Possible structures of cycle-connected and homochromatic ears, where is indicated by a solid line

XU introduced the tree-coloring and cycle- coloring in Ref. [26]. For the convenience of description, we restate them here. Letbe a 4- colorable maximal planar graph with color set,. Ifsuch thathas a cycle, thenis referred to as a cycle- coloring, and we callis cycle-colorable. Conversely, if,contains no cycle, thenis referred to as a tree-coloring of, andis tree-colorable. Ifis tree-colorable (cycle-colorable) but not cycle-colorable (tree- colorable), theis also called purely tree- colorable (purely cycle-colorable). Furthermore, ifis both tree-colorable and cycle-colorable, thenis also called mixed colorable. Obviously, for any 4-colorable maximal planar graphcolorings incan be partitioned into two classes: cycle-colorings and tree-colorings.

a Kempe equivalent class of.

An 11-order maximal planar graph shown in Fig. 6 has totally eight 4-colorings, denoted byrespectively. Forit is not difficult to see;;Moreover,has seven 2-colorable cyclesin total, thus.

The following is a straight forward result by the definition of-operations:

In this section, we introduce-characteristic graphs forwhich clearly chara-

cterize the relations of all 4-colorings of.

Fig. 6 Examples of complementary colorings

Fig. 7 Thecharacteristic graph and its topological structure of the graph shown in Fig. 6

Theorem 3 For a 4-colorable maximal planer graph, letbe thegraph of. We have

(1)is a uniquely four-colorable maximal planar graph if and only if;

Among all maximal planar graphs with order at most 11, tree-colorings account for about 2 percent of all 4-colorings[26]. We conjecture that the number of tree-colorings is much less than that of cycle-colorings of maximal planar graphs with. Hence, for a given cycle-coloringof a 4-chromatic maximal planar graphit is possible to derive all 4-colorings offromby means of the

Proof By contradiction. Suppose thatcontains a triangleWithout loss of generality, we assume

Fig. 8 The first case of the proof of the Theorem 5: are disjoint

not contain any 2-chromatic cycle, such thatandare two complementary colorings respect to; a contradiction.

Fig. 9 The second case of the proof of the Theorem 5: are joint.

This completes the proof of Theorem 5.

By Theorem 5, it has that thecharacteristic graphof a 4-colorable maximal planar graphwithis triangle-free, which means that the induced subgraphis a star, whereis the closed neighborhood of vertexin. So, we have,

Corollary 1 Letbe a 4-colorable maximal planar graph with. Then, for any cycle- coloring, the induced graphis a star.

Fig. 10 The diagram for the proof of Theorem 6

Proof To the contrary, suppose thatare two adjacent vertices insuch thatandLetbe the unique 2-chromatic cycle of, and letcontain two joint 2-chromatic cyclesClearly,andare complementary respect toWithout loss of generality, assume that,. We useto denote the subgraphs ofinduced byand, respectively, and useto denote the number ofcomponents inforand

Since the graph, under the coloring, has a unique 2-chromatic cycle, we have thatconsists of two connected components, and,are connected. Now, we can see that the14-components ofare connected to a component by the14-paths of; and the13-components ofare connected into one component by the13-paths of

Then, we can obtain a 4-coloringby exchanging the colors of 34-componentinside. Under the coloring, it is easy to see that the number of 13-components inis, andstill contains13-paths with both the initial vertex and the terminus vertex on. Because all of these 13-paths connect the13-components ofinto a component with a 13-cycle, it has that. In addition, the number of 14-components inis changed into, andstill contains14-paths with both the initial vertex and the terminus vertex on. Because, it follows that the14- components incan not be connected into a component by the14-paths. Hence,is disconnected under the coloring,..contains a 2-chromatic cycle, and a contradiction. Hence, the result holds.

4 Types of Kempe Equivalent Classes of Non-Kempe Graphs

4.1 Tree-type Kempe equivalent class

It follows that

4.2 Cycle-type Kempe equivalent classes

In Eq. (11), we do not consider the colors on 2-chromatic cycles inand. That is to say, for a 2-chromatic cycleboth inand,may be different from.

Obviously, the cycle-coloringsatisfying Eq. (11) is also a 2-chromatic unchanged-cycle coloring of. The cycle-type maximal planar graph shown in Fig. 11 has totally four 4-coloringsandwhereandare two complementary 2-chromatic unchanged-cycle colorings respect toand the unique 2-chromatic unchanged-cycle of them is 12-cycle.

Fig. 11 An example of cycle-type maximal planar graph containing only one 2-chromatic unchanged-cycle

Fig. 12 Two maximal planar graphs containing two 2-chromatic unchanged-cycles

Proof The result follows from definitions of the 2-chromatic colorable-cycles andoperations.

For two 2-chromatic cycles with the condition of Theorem 9, it is easy to see that these two cycles are breakable. However, we can not break a 2-chromatic unchanged-cycleofby implementing a series ofwith.. we can not obtain asatisfying Eq. (12) throughandSo,andare not Kempe equivalent. The root reason whyandare not Kempe equivalent is the 2-chromatic unchanged-cycle. We refer to such equivalent classas a cycle-type Kempe equivalent class. For a 4-coloring set containing exactly2-chromatic unchanged-cycles, the induced subgraph ininduced by this set is ahypercube. The-dimensional hypercube graph (-hypercube for short), written asis a-regular graph with vertex set

Clearly, the following Eq. (15) holds.

On the other hand, without loss of generality, we assume that the0-1 sequence corresponding toisLetbe the resulting coloring after implementing arespect toThen,induces exactlycomplementary colorings. Similarly, we can prove that each coloringinduces exactlycomplementary colorings. Therefore, we can further prove that each 4-coloring of thecolorings exactly inducescomplementary colorings. Notice that each 4- coloring can induce its complementary coloring if and only if the Hamming distance between the two0-1 sequences corresponding to the two coloring is equal to 1. Hence, the graph formed by this0-1 sequences corresponding to the4-colorings is a hypercube.

Now, a question naturally arises. Is any 2- chromatic cycle of any 4-coloring breakable? The answer is positive, we will deal with the issue in later articles of this series. We propose it as a conjecture here.

4.3 Circular-cycle-type Kempe equivalent classes

Fig. 13 Two examples of cycle-type and circular-cycle-type Kempe equivalent classes

From the two examples shown in Fig. 13, the Kempe equivalent class induced by a 4-coloringofis of one of the following types.

Pure cycle type It contains one or more 2-chromatic unchanged-cycles, as shown in Fig. 11 and Fig. 12.

Mixed type It contains not only 2-chromatic unchanged-cycle but also circular 2-chromatic cycle, see Fig. 13(a).

Pure circular-cycle type It contains one or more circular 2-chromatic cycles. See the coloringshown in Fig. 13(b) that contains two circular 2-chromatic cycles.

Remark 1 There exists some graph that has the same 2-chromatic cycle under different colorings of the graph, but these colorings belong to different Kempe equivalent classes.

5 Kempe Graphs

If a 4-colorable maximal planar graphwithis a Kempe graph, then we can induce all 4-colorings offrom a given 4-coloring byTo characterize such graphs, this section introduces a method to recursively construct Kempe graphs based on the extending domino configuration operations, and proposes two conjectures.

5.1 A conjecture of Kempe graphs

For a 4-colorable maximal planar graphwith, ifis a non-Kempe graph, then there are three types of Kempe equivalent classes: tree-type, cycle-types, and circular-cycle-type.

The Conjecture 3 is relevant to Uniquely Four- Colorable Maximal Planar Graph Conjecture. If the Uniquely Four-Colorable Maximal Planar Graph Conjecture is true, that is, every uniquely four-colorable maximal planar graph is a recursive maximal planar graph[26], then each 4-colorable maximal planar graphwithhas at least two different 4-colorings. Ifis tree-type, thenis not a Kempe graph, because any tree coloring can not induce any other 4-coloring ofby-operations.

The Conjecture 3 is also relevant to Conjecture 2. Suppose that there exists a 4-coloringwith a 2-chromatic unchanged-cycle. If Conjecture 2 is true, then the cycleis breakable. Consequently,, such that. Butandare unreachable by theoperations. Therefore,is not a Kempe graph.

However, even if the Conjecture 3 turns out to be true, we can not know the characteristics of Kempe graphs from its types of Kempe equivalent classes. For further research on Kempe graphs, we then propose the domino recursive construction method.

5.2 Constructions of Kempe graphs

In the second paper of this series of articles[25], we proved that every maximal planar graphwith orderandhas an ancestor-graph of orderorand minimum degree not less than 4. In other words, there are at least one of five basic domino configurations of Fig. 14 in. For convenience of statement, we write these five basic domino configurations shown in Fig. 14 asand.

Fig. 14 Five basic domino configurations

Given that the natural coloringobtained by implementing a domino extending wheel operation under a 4-coloring, we can prove Theorem 11 through the following three cases: one ofandis tree-type; one ofandis cycle-type; one ofandis circular cycle-type.

A further research on Kempe maximal planar graphs will be given in later papers of this series of articles, which include the proofs of Theorem 11 and Conjecture 4, as well as the relations betweenand,.

6 Conclusion and Prospection

It is generally known that showing the characteristics of Kempe graphs is still a difficult and hot problem. Although there are many literatures in this field, it is hard to find any necessary and sufficient condition of aKempe graph. Hence, the currently main research focuses on the Kempe equivalence of some special graphs, such as regular graphs. In this series of articles we are concerned with maximal planar graphs.

The main contributions of this paper are summarized as follows: (1) We observe that the inner mechanism that two 4-colorings in maximal planar graphs being Kempe equivalent is closely related with a class of subgraphs, called 2- chromatic ears. So we make an in-depth research on 2-chromatic ears. (2) We introduce and explore the properties ofgraphs, which clearly characterize the relations of all 4-colorings of(3) We partition the Kempe equivalent classes of non-Kempe graphs into three classes: tree-type, cycle-type, and circular-cycle-type, and point out that all these three classes can exist simultaneously in the set of 4-colorings of one maximal planar graph. (4) In terms of Kempe maximal planar graphs, we make a research on their characteristics, put forward a recursive domino method to construct such graphs, and conjecture thatandare two Kempe maximal planar graphs if and only if the number of potential 4-chromatic funnel subgraphs ofis less than two.

We will gradually make comprehensive in- depth studies on three types of Kempe equivalent classes of non-Kempe graphs in later papers of this series of articles. Especially, we will show a necessary and sufficient condition of Kempe maximal planar graphs.

Acknowledgements The author would like to thank Professors Yao Bing, Chen Xiang’en, Wu Jianliang, and the author’s students Wang Hongyu, Liu Xiaoqing, Zhu Enqiang, Li Zepeng, Zhou Yangyang and Zhao Dongyang for useful discussions. Finally, the author would especially like to thank the Academician He Xingui and Processor Yu Daoheng of Peking University for their reviews, selfless supports, and encouragements to accomplish this work.

References

[1] JENSEN T R and TOFT B. Graph coloring problems[J].-, 1995, 113(2): 29-59. doi: 10.1002/ 9781118032497.ch2.

[2] DIAZ J, PETIT J, and SERNA M. A survey of graph layout problems[J]., 2002, 34(3): 313-356. doi: 10.1145/568522.568523.

[3] BRODER A, KUMAR R, MAGHOUL F,Graph structure in the web[J]., 2000, 33(1/6): 309-320. doi: 10.1016/S1389-1286(00)00083-9.

[4] XU J, LI Z P, and ZHU E Q. Research progress on the theory of maximal planar graphs[J]., 2015, 38(8): 1680-1704. doi: 10.11897/SP.J.1016.2015. 01680.

[5] KEMPE A B. On the geographical problem of the four colors[J]., 1879, 2(3): 193-200. doi: 10.2307/2369235.

[6] FISK S. Geometric coloring theory[J].,1977, 24(3): 298-340. doi: 10.1016/0001- 8708(77)90061-5.

[7] MEYNIEL H. Les 5-colorations d'un graphe planaire Forment une classe de commutation unique[J]., 1978, 24(3): 251-257. doi: 10.1016/0095-8956(78)90042-4.

[8] VERGNAS M L and MEYNIEL H. Kempe classes and the Hadwiger conjecture[J]., 1981, 31(1): 95-104. doi: 10.1016/S0095- 8956(81)80014-7.

[9] MOHAR B. Kempe Equivalence of Colorings[M]. Graph Theory in Paris, Birkhäuser Basel, 2006: 287-297. doi: 10.1007/978-3-7643-7400-6_22.

[10] FEGHALI C, JOHNSON M, and PAULUSMA D. Kempe equivalence of colourings of cubic graphs[J]., 2015, 49: 243-249. doi: 10.1016/j. endm.2015.06.034.

[11] CERECEDA L, HEUVEL J V D, and JOHNSON M. Connectedness of the graph of vertex-colourings[J]., 2008, 308(5/6): 913-919. doi: 10.1016/j.disc. 2007.07.028.

[12] MCDONALD J, MOHAR B, and SCHEIDE D. Kempe equivalence of edge-colorings in subcubic and subquartic graphs[J]., 2012, 70(2): 226-239. doi: 10.1002/jgt.20613.

[13] BELCASTRO S M and HAAS R. Counting edge-Kempe- equivalence classes for 3-edge-colored cubic graphs[J]., 2014, 325(13): 77-84. doi: 10.1016/j. disc.2014.02.014.

[14] FIOL M A and VILALTELLA J. A simple and fast heuristic algorithm for edge-coloring of graphs[J]., 2013, 10(3): 263-272.

[15] EFTHYMIOU C and SPIRAKIS P G. Random sampling of colourings of sparse random graphs with a constant number of colours[J]., 2008, 407(1/3): 134-154. doi: 10.1016/j.tcs.2008.05.008.

[16] DYER M, FLAXMAN A D, FRIEZE A M,. Randomly coloring sparse random graphs with fewer colors than the maximum degree[J]., 2006, 29(4): 450-465. doi: 10.1002 /rsa.20129.

[17] HAYES T P and VIGODA E. A non-Markovian coupling for randomly sampling colorings[C]. 44th Annual Symposium on Foundations of Computer Science, 2003: 618-627. doi: 10.1109/SFCS.2003.1238234.

[18] LUCZAK T and VIGODA E. Torpid mixing of the Wang- Swendsen-Kotecky algorithm for sampling colorings[J]., 2005, 3(1): 92-100. doi:

10.1016/j.jda.2004.05.002.

[19] MORGENSTERN C A and SHAPIRO H D. Heuristics for rapidly four-coloring large planar graphs[J]., 1991, 6(1): 869-891. doi: 10.1007/BF01759077.

[20] SIBLEY T and WAGON S. Rhombic penrose tilings can be 3-colored[J]., 2000, 107(3): 251-253. doi: 10.2307/2589317.

[21] VIGOD E. Improved bounds for sampling colorings[C]. 40th Annual Symposium on Foundations of Computer Science, New York, 1999: 51-59. doi: 10.1109/SFFCS.1999.814577.

[22] FRIEZE A and VIGODA E. A survey on the use of Markov chains to randomly sample colourings[C]. In Combinatorics, Complexity, and Chance. Oxford Lecture Ser. Math. Appl. 34 53-71. Oxford Univ. Press, Oxford. MR2314561doi: 10.1093/acprof:oso/9780198571278.003.0004.

[23] HAYES T P and VIGODA E. Coupling with the stationary distribution and improved sampling for colorings and independent sets[J]., 2006, 16(3): 1297-1318. doi: 10.1214/105051606000000330.

[24] BALASUBRAMANIAN R and SUBRAMANIAN C R. On sampling colorings of bipartite graphs[J]., 2006, 8(1): 17-30.

[25] XU J. Theory on structure and coloring of maximal planar graphs (2) Domino configurations and extending- contracting operations[J].&, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT160224.

[26] XU J. Theory on structure and coloring of maximal planar graphs (3) Purely tree-colorable and uniquely 4-colorable Maximal Planar Graph Conjectures[J].&, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

[27] BONDY J A and MURTY U S R. Graph Theory[M]. Springer, 2008: 6-58.

2016-05-11; Accepted: 2016-05-30; Online published: 2016-06-02

XU Jin jxu@pku.edu.cn

The National 973 Program of China (2013CB 329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

1)Liu Xiaoqing, Xu Jin, submitted to Dis. Math.

O157.5

A

10.11999/JEIT160483

XU Jin: Born in 1959, Professor. His main research includes graph theory and combinatorial optimization, biocomputing, social networks, and information security.