小波结合双边滤波抑制全息相干噪声

肖 文，王庆伍，潘 锋



小波结合双边滤波抑制全息相干噪声

肖 文，王庆伍，潘 锋

( 北京航空航天大学 仪器科学与光电工程学院，北京 100191 )

抑制数字全息中相干噪声可以获得更高质量的数字全息再现图像。本文提出一种结合双边滤波和小波邻域阈值的数字全息相干噪声抑制方法。对再现像进行小波变换，利用小波邻域方法对高频分量小波阈值去噪，对低频分量做双边滤波处理，最后做小波逆变换得到去噪再现像。通过仿真分析将该方法与中值、均值、维纳滤波等方法进行了比较，去噪后所得图像的峰值信噪比提高了0.4 dB~2 dB，与原始图像的相关性更高。利用全息实验数据验证了方法，结果表明本文方法能够有效抑制散斑噪声，同时更好的保留再现像的细节信息。

数字全息；相干噪声；散斑抑制；小波变换；双边滤波

0 引 言

数字全息技术[1]是基于传统全息原理，借助光电图像探测和计算机图像处理技术，利用CCD或CMOS传感器以数字形式记录全息图，然后通过计算机模拟光学衍射过程来实现全息再现，能够定量获得物体的振幅和相位像。数字全息作为一种相干成像技术，通常采用激光器作为光源。由于激光具有较好的时间和空间相干性，当物体具有粗糙表面或折射率不均匀等特性，以及光路中存在多层反射面、划痕、灰尘颗粒等因素，将产生寄生条纹、散斑分布等相干噪声[2]，并与物光场同时记录在全息图中。因此数字再现时，相干噪声也被重构再现，这将严重影响再现像质量，使得再现图像分辨率降低，图像细节结构模糊，降低测量精度。因此，在数字全息中抑制相干噪声是非常必要的。

目前全息相干噪声抑制方法主要有两类。一类是在全息图获取过程中运用光学方法[3-7]，例如采用弱相干或非相干光源，但是该方法对光路的结构及其稳定性有严格要求。另外通过多波长、多偏振态、多角度照明等方式记录多幅全息图。这些方法的物理基础是各全息图记录了同一物的光场，但具有不同相干噪声分布。进而通过平均叠加处理实现相干噪声抑制。这些方法的局限性在于增加了光路结构和记录过程的复杂性。另一类方法是运用图像处理技术对再现像进行去噪处理。例如Garcia-Sucerquia[8]等人采用中值滤波和均值滤波减小激光相干散斑颗粒。Maycock[9]等人采用傅里叶滤波法滤除相干散斑噪声。Sharma[10]等人采用小波变换滤除相干散斑噪声。蔡晓鸥[11]等用带孔径函数的维纳滤波法滤除散斑噪声。贾勤[12]等人利用边缘检测结合小波变换的方法有效抑制了全息再现像的激光散斑。Uzan等人利用NLM滤波算法[13-14]对数字全息散相干噪声进行抑制。Montresor等人将均值、维纳、小波等滤波方法对全息图降噪效果进行了对比。与第一类方法相比，这类方法的优势在于不需要任何硬件支持，仅通过对全息再现像的后处理来进行噪声抑制，其代价最小。

然而基于图像处理技术来抑制相干噪声方法面临的共同问题是抑制噪声的同时会损失部分再现像的细节信息，即影响图像的分辨率。针对这一矛盾，本文提出一种结合双边滤波的小波邻域阈值相干噪声抑制方法。针对全息再现像的小波变换高频分量利用邻域阈值进行阈值萎缩，而对其低频分量利用双边滤波进行滤波，这样将两种滤波方法的优势都利用起来，同时弥补了其各自不足，实现全息再现像去噪的同时更好的保留图像的细节信息。

1 结合双边滤波的小波邻域阈值抑制全息相干噪声算法

基于Goodman完全发育的相干散斑噪声特性，数字全息相干散斑噪声可近似为一种均匀分布乘性噪声模型。其模型为

式中：表示受噪声影响的再现像，表示物体再现像，表示散斑噪声，、分别代表再现像横纵像素。对式(1)作对数运算，将再现像乘性噪声转换为加性噪声进行处理，得到：

此时散斑噪声转化为加性噪声ln，是近似服从零均值高斯分布的。

基于小波变换具有多分辨率、去相关性、选基灵活性等特点，本文将采用小波阈值滤波结合双边滤波来进行相干噪声抑制。首先，对全息再现像进行小波变换，得到一个低频分量及若干尺度的三方向高频分量。然后，对高频分量利用邻域阈值进行阈值萎缩，保留高频细节的同时抑制噪声。一般小波滤波方法中低频分量是不进行滤波处理的。由于相干散斑场与物光场叠加是随机的，使得散斑频谱与物光频谱产生混淆，导致再现像进行小波变换后，其低频分量中也含有部分颗粒状相干噪声。基于这一特点，在利用小波变换抑制全息相干噪声过程中，有必要对低频分量进行去噪处理。双边滤波[15]在保留图像的基本特性，如结构、纹理、平均强度等信息是有优势的，因此选用双边滤波来对再现像的低频分量进行处理。通过综合利用小波阈值方法以及双边滤波方法，在一定程度上缓解了图像处理抑制相干噪声的共同矛盾，抑制散斑的同时较好地保留了数字全息再现像的细节信息，从而得到更高质量的数字全息再现像。

本文综合滤波算法的流程如图1所示。

具体步骤如下：

1) 再现像对数化 通过对数化操作，将再现像中的乘性散斑噪声转化为近似高斯分布的加性噪声。

图1 滤波流程图

2) 再现像小波分解为了获得原图像大小一致的高频分量，采用平稳小波变换，对对数化再现像进行小波分解。得到3+1个子带(为分解尺度)，其中低频子带LL一个，高频子带共3个,分别为水平方向高频分量HL，垂直方向高频分量VH，对角方向高频分量HH(=1，2，…，)。

3) 低频分量LL双边滤波去噪运用平移不变高斯滤波器对小波分解的低频分量进行处理，在实现滤除噪声的同时保护了低频分量中的图像特征。利用低频分量小波系数区域位置相似性和绝对值相似性构造了双边滤波器中区域滤波器和值域滤波器。

其中：为待滤波低频分量像素，为邻域内像素，邻域大小为(2+1)×(2+1)；及分别为低频分量空间临近度函数及小波系数值相似函数，均取为参数间欧几里德距离的高斯函数；参数为邻域空间方差，决定了邻域权重因子衰减系数；为灰度方差，控制着值域权重因子衰减系数。

4) 高频分量小波邻域阈值去噪小波去噪中阈值的选择对去噪结果影响明显。阈值过大则容易造成过度平滑，阈值太小则噪声去除效果不佳。考虑到再现像的邻域小波系数相互之间具有强相关性，而噪声是独立分布的，其邻域内小波系数几乎没有相关性这一特点。本文选用小波NeighShrink阈值[16]对再现像小波分解的高频分量进行阈值处理，实现噪声与图像高频信息的分离。

NeighShrink阈值是根据邻域内小波系数相关性来确定阈值，与系数越近，相关性越强。综合考虑相关性以及运算效率，邻域窗口选择为3×3或5×5。以邻域窗口内小波系数的平方总和与通用阈值进行比较，为图像总像素数。当平方总和小于，则认为窗口中心的小波系数由噪声产生，直接置零；反之，则对窗口中心的小波系数作收缩运算。小波系数的平方和和收缩因子及收缩运算的计算表达式分别为

5) 小波逆变换利用处理后的低频分量及高频分量作小波逆变换，得到抑制噪声后的再现像。

2 仿真分析

2.1 仿真数据

本文方法将与文献[8]中均值滤波、中值滤波算法、文献[11]中所用维纳滤波算法、文献[16]中提出的双边滤波、文献[12]中所用结合边缘检测的小波滤波等算法进行比较。图像选择cameraman、lena、mandrill、barbara四幅图片，通过将均值为0，方差为0.1的均匀分布的随机Speckle乘性噪声模拟相干散斑噪声，再对含噪图像进行对数化处理，将乘性噪声转化为加性噪声，此时仿真图像中噪声模型实际全息图可用式(2)来表示。为保持统一，用于比较的均值、中值、维纳小波邻域滤波算法中邻域窗口一律设定为5×5。双边滤波邻近阈值及系数阈值分别设定为2及0.2。采用定量评价参数均方差MSE(用表示)、峰值信噪比PSNR(用表示)和相似度来衡量去噪结果，其表达式分别为：

2.2 仿真结果及分析

表1为加噪图像以及经六种不同方法去噪后的图像与原始图像进行比较，计算出的各自峰值信噪比以及结构相似度统计结果。图2为纹理、细节信息最丰富的mandrill图像胡须附近区域去噪结果对比图，图3是lena图像去噪结果对比图。图2及图3中(a)是原始图像，(b)是加噪后图像，(c)是加噪图像经均值滤波结果，(d)是加噪图像经中值滤波结果，(e)是加噪图像经维纳滤波结果，(f)是加噪图像经双边滤波结果，(g)是加噪图像经小波结合边缘检测方法滤波结果，(h)为加噪图像经本文方法滤波所得结果。

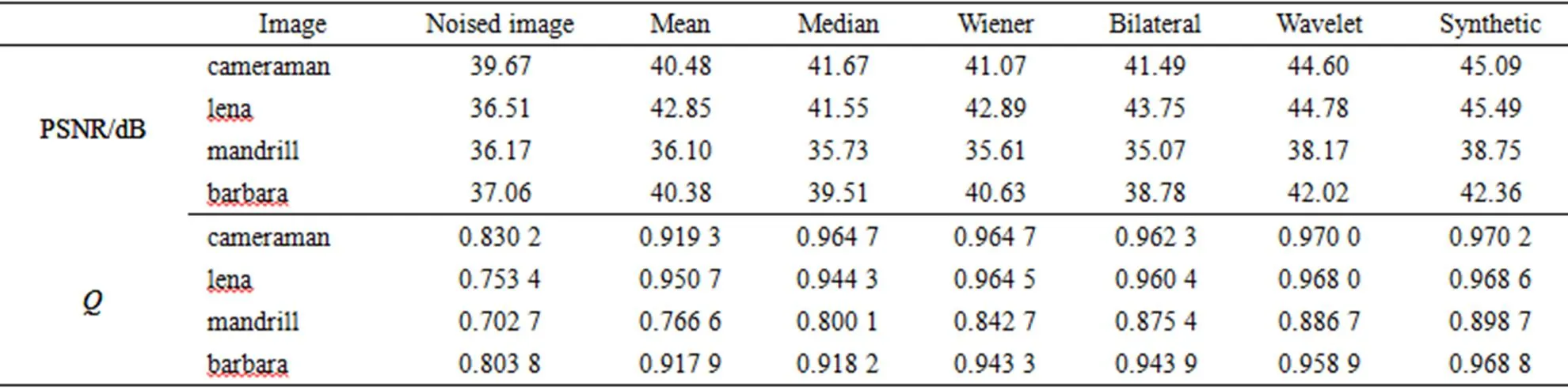
表1 滤波结果对比表Table 1 Comparison table of filtering results

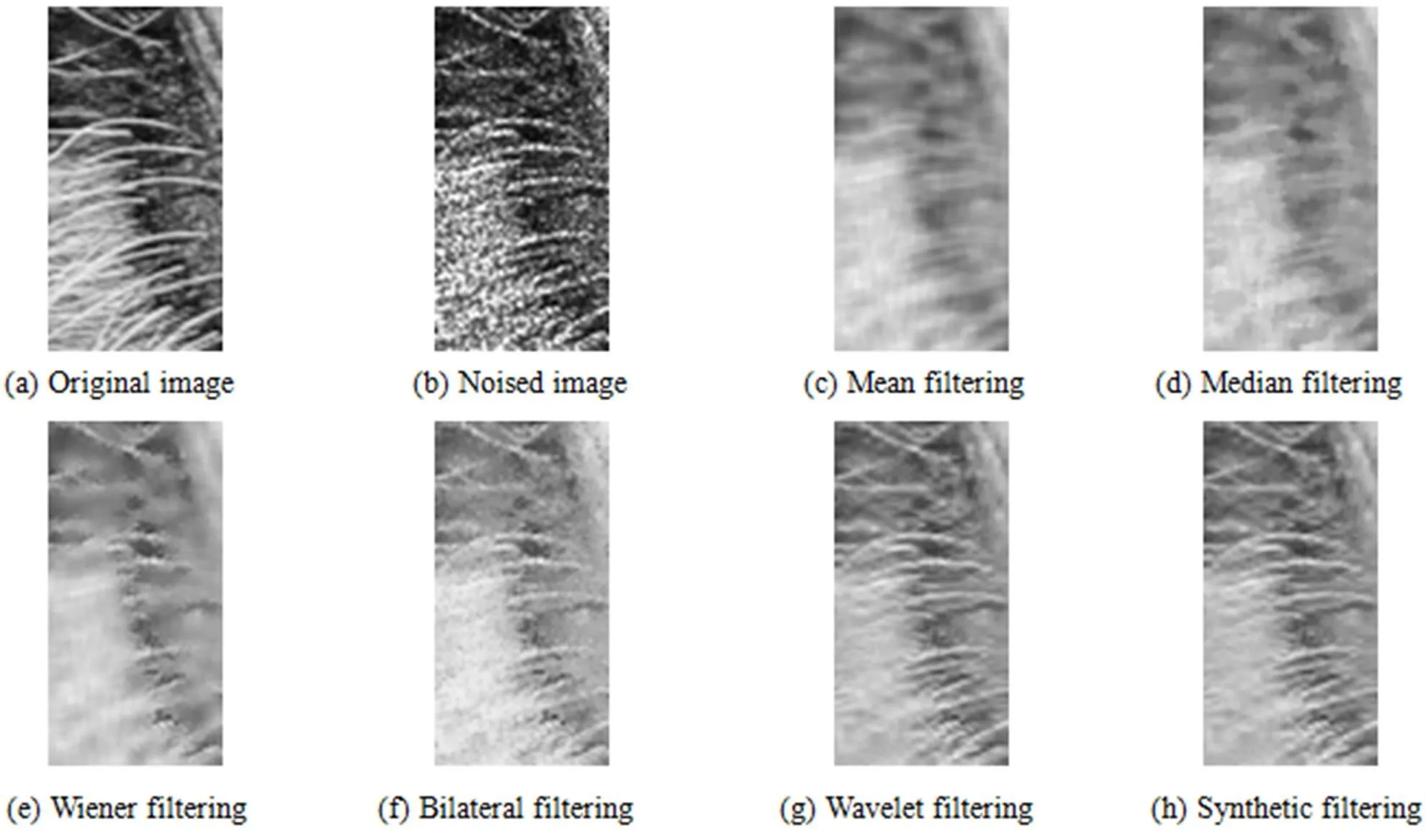
图2 mandrill区域截图

图3 Lena滤波组图

通过表1，可以看出运用本文方法去噪后图像的PSNR值比其它方法都要高0.5 dB至4 dB，同时与原始图像相比其结构相似度也最高，细节信息保持最好。从lena去噪组图也可以看出，本文方法相干噪声去除效果好，同时从lena的帽子、头发和眼睫毛等也可看出，图像细节信息保持较好。而在mandrill细节信息最为丰富的胡须区域截图也可以看出，本文方法处理后狒狒(mandrill)的胡须边缘轮廓清晰、细节结构保持较好。由此可见本文方法与相比较的其它传统去噪方法不仅去噪效果好，在保持细节信息上具有优势。

3 实验验证

3.1 实验系统

实验对象选定色子、硬币和分辨率板，三者材质分别为塑料、金属、玻璃，表面粗糙程度差异较大。实验光路图如图4。激光器发出的激光束进入偏振分光棱镜(PBS)分为两束。两束光分别经空间滤波器扩束并经透镜L1和L2准直，其中一束光经被测物反射后携带物面信息，即作为物光与另一束参考光沿入射方向被合光棱镜(BS)接收。两光束以小角度在CCD相机光敏面上相干叠加，产生离轴全息图，进而传送到计算机进行再现计算。其中光源为Nd:YAG固体激光器，波长为532 nm，输出功率为15 mW，相干长度约为50 m。CCD相机像素数1 024 pixel×1 024 pixel，像素尺寸6.7 μm×6.7 μm。

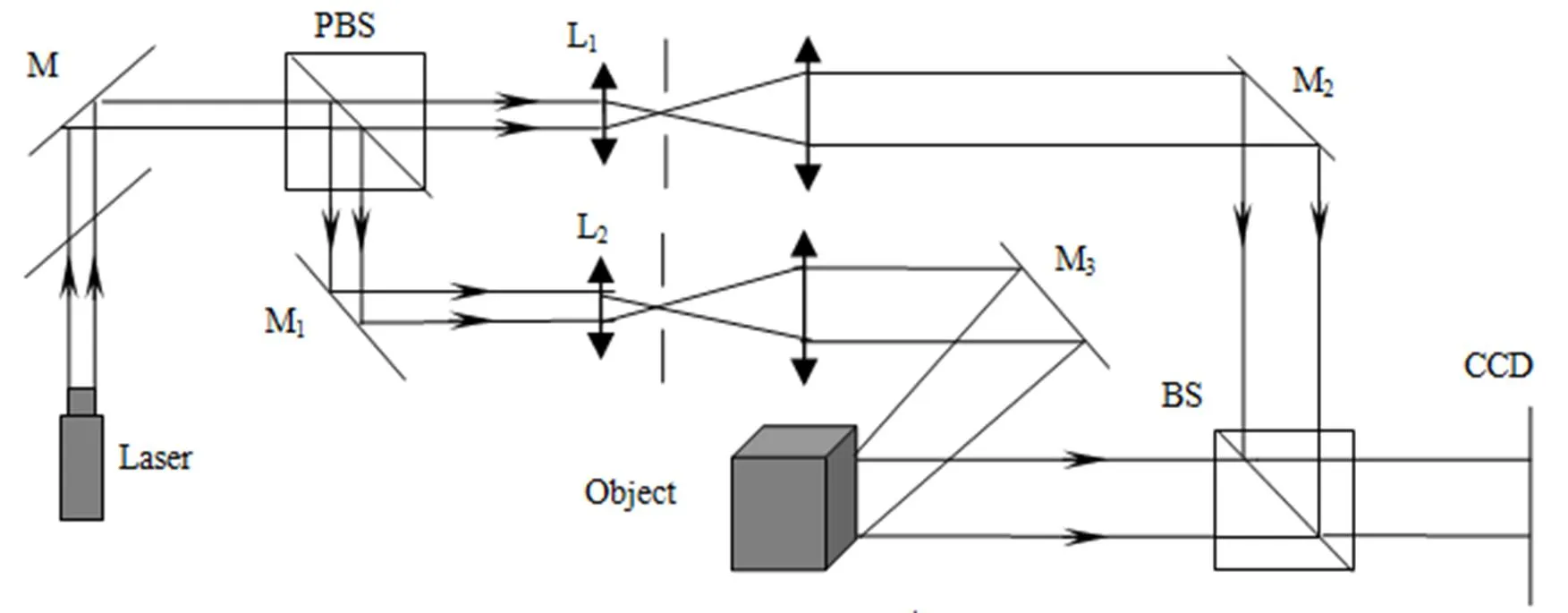
图4 实验光路结构示意图

3.2 实验结果与分析

图5及图6分别是硬币以及色子的再现图像滤波结果对比图。图5及图6中(a)是原始再现像，(b)是经均值滤波结果，(c)是经中值滤波结果，(d)是经维纳滤波结果，(e)是经双边滤波结果，(f)是经小波滤波结果，(g)为经本文方法滤波所得结果。

由图5和6可以看出，相比于其它方法，本文方法去噪后硬币和色子表面颗粒状相干散斑噪声消除得最好。同时，为了定量比较，用相干散斑指数来评价滤波算法对散斑的抑制能力。散斑指数(Speckle index，用表示)[17]定义为

图5 硬币滤波对比图

图6 色子滤波对比图

表2 散斑指数统计表Table 2 Speckle index statistics

进一步利用分辨率板再现像进行比较。图7中(a)、(b)、(c)、(d)分别是分辨率板再现像原始图像，利用双边滤波去噪后的再现像，利用小波邻域阈值去噪后的再现像，结合小波邻域阈值及双边滤波去噪后的再现像。图7(a)中白线位置属于分辨率板中平坦区域，在不受相干噪声影响的理想状态下，其再现像上灰度值理应趋于一个定值。图8是针对图7(a)中白线位置，对图7(b)、7(c)、7(d)同样位置直线上像元灰度值分析图。图8横坐标为像素位置，纵坐标为像素归一化灰度值，实线为小波邻域去噪结果、短虚线为双边滤波去噪结果、双点间断虚线为本文所用方法去噪结果，单点间断虚线为白线上灰度值平均值。可看出本文方法去噪后，蓝色曲线像元灰度值变化减缓，平坦区域基本处于同一水平，更逼近于灰度平均值，去噪效果最好。

图7 分辨率板滤波对比图

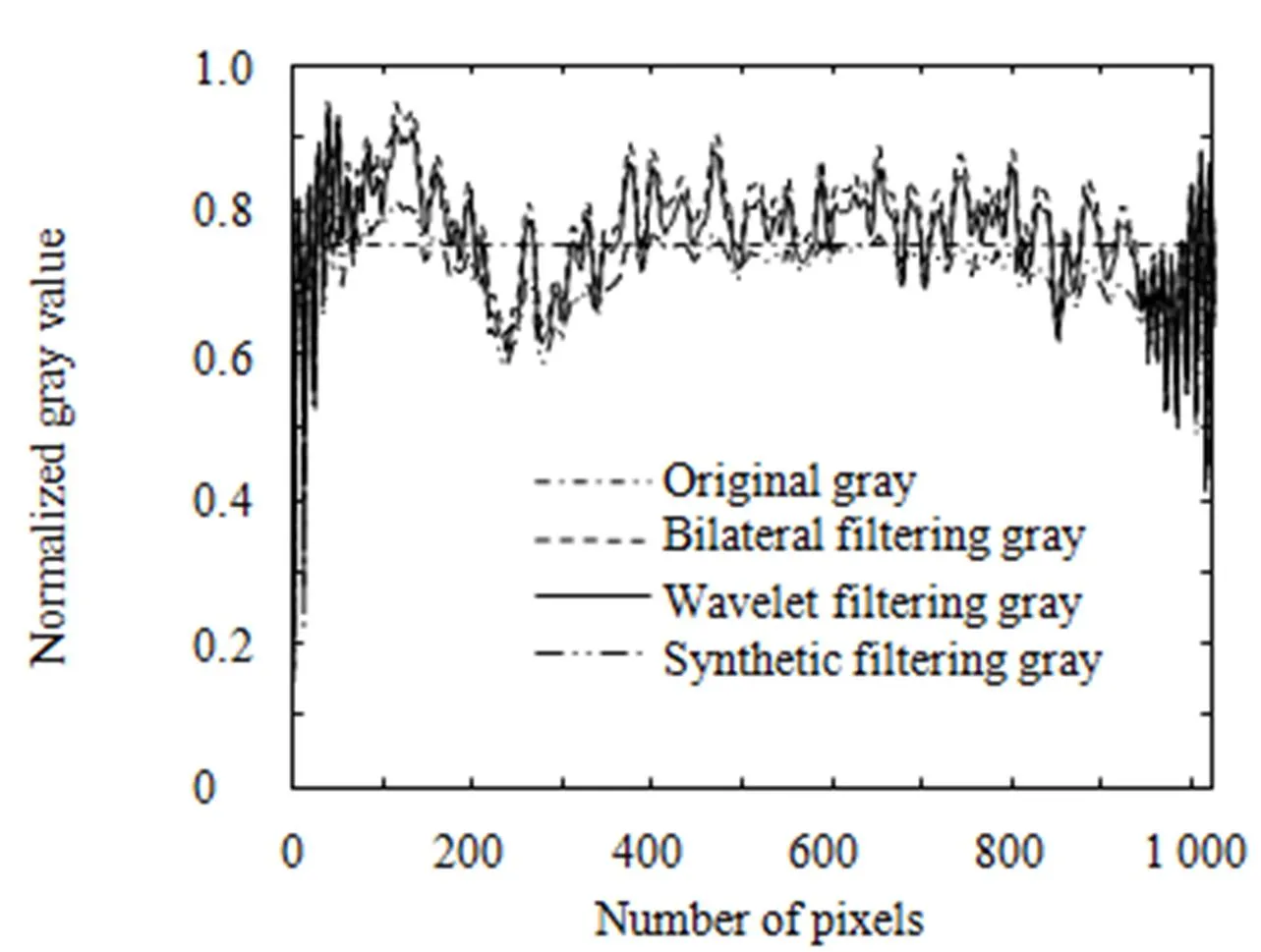
图8 灰度变化对比图

4 结 论

本文提出了一种结合小波阈值去噪及双边滤波来抑制数字全息相干散斑噪声的方法。针对此方法，首先进行仿真分析，利用均方差MSE、峰值信噪比PSNR和相似度三项指标对仿真结果进行了定量分析，结果表明本文方法均方差更小，峰值信噪比更大，去噪后的图像在边缘、纹理、结构与原始图像更接近。然后，开展数字全息实验，对本方法的有效性和优越性进行了实验验证。基于表面较粗糙的色子、硬币和表面光滑的分辨率板的再现像，将本方法与其它方法的去噪结果进行定性和定量的比较分析。结果表明，相比于其它方法，本文结合双边滤波的邻域小波阈值去噪方法，不仅抑制相干散斑噪声效果好，同时去噪后图像与原图像相关度最高，对再现像的细节信息保留更完整。

[1] Goodman J W，Awrence R W. Digital image fortnulation form electronically detected holograms [J]. Applied Physics Letters (S0003-6951)，1967，11(2)：77-79.

[2] 张亦卓. 生物样品的数字全息显微相衬成像技术研究 [D]. 北京：北京工业大学，2012：40-41.

ZHANG Yizhuo. Digital holographic microscopy study of biological samples phase contrast imaging technique [D]. Beijing：Beijing University of Technology，2012：40-41.

[3] XIAO Wen，ZHANG Jing，RONG Lu，. Improvement of speckle noise suppression in digital holography by rotating linear polarization state [J]. Chinese Optics Letters(S1671-7694)，2011，9(6)：0609011-0609013.

[4] PAN Feng，XIAO Wen，LIU Shuo，. Coherent noise reduction in digital holographic phase contrast microscopy by slitly shifting object [J]. Optics Express(S1094-4087)，2011，19(5)：3862-3869.

[5] 王大勇，王云新，郭莎，等. 基于多角度无透镜傅里叶变换数字全息的散斑噪声抑制成像研究 [J]. 物理学报，2014，63(15)：175-180.

WANG Dayong，WANG Yunxin，GUO Sha，. Research on speckle denoising by lensless Fourier transform holographic imaging with angular diversity [J]. Acta Physica Sinica，2014，63(15)：175-180.

[6] LI Dayan，Damien P Kelly，John T Sheridan. Speckle suppression by doubly scattering systems [J]. Applied Optics (S1539-4522)，2013，52(35)：8617-8626.

[7] 张雯，周皓，顾济华，等. 多光束数字全息的研究 [J]. 光子学报，2010，39(3)：533-536.

ZHANG Wen，ZHOU Hao，GU Jihua，. Multi-beamdigital holography [J]. Acta Photonics Sinica，2010，39(3)：533-536.

[8] Jorge Garcia-Sucerquia，Jorge Alexis Herrera Ramírez，Daniel Velásquez Prieto. Reduction of speckle noise in digital holography by using digital image processing [J]. Optik-International Journal for Light and Electron Optics(S0030-4026)，2005，116(1)：44-48.

[9] Jonathan Maycock，Bryan M Hennelly，John B Mcdonald，. Reduction of speckle in digital holography by discrete Fourier filtering [J]. Journal of the Optical Society of America A(S1084-7529)，2007，24(6)：1617-1622.

[10] Akshay Sharma，Gyanendra Sheoran，Jaffery Z A，. Improvement of signal-to-noise ratio in digital holography using wavelet transform [J]. Optics & Lasers in Engineering(S0143-8166)，2008，46(1)：42-47.

[11] CAI Xiao¢ou. Reduction of speckle noise in the reconstructed image of digital holography [J]. Optik-International Journal for Light and Electron Optics(S0030-4026)，2010，121(4)：394-399.

[12] 贾勤，李志全. 数字全息再现图像散斑噪声消除新方法 [J]. 计算机工程与应用，2012，48(9)：205-207.

JIA Qin，LI Zhiquan. Speckle denoising new method for reconstructed image of digital holography [J]. Computer Engineering and Applications，2012，48(9)：205-207.

[13] Uzan A，Rivenson Y，Stern A. Speckle denoising in digital holography by nonlocal means filtering [J]. Applied Optics (S1539-4522)，2013，52(1)：195-200.

[14] Jaehong Aum，Ji-hyun Kim，Jeong Jichai. Effective speckle noise suppression in optical coherence tomography images using nonlocal means denoising filter with double Gaussian anisotropic kernels [J]. Applied Optics(S1539-4522)，2015，54(13)：D43-D50.

[15] Tomasi C，Manduchi R. Bilateral filtering for gray and color images [C]// Proceedings of the Sixth International Conference on Computer Vision，New Delhi，India，Jan 4-7，1998：839-846.

[16] Dongwook C，Tien D B，CHEN Guangyi. Image Denoising based on Wavelet Shrinkage Using Neighbor and Level Dependency [J]. International Journal of Wavelets Multiresolution and Information Processing(S0219-6913)，2009，7(3)：299-311.

[17] Dewaele P，Wambacq P，Oosterlinck A，. Comparison of some speckle reduction techniques for SAR images [Z]. Geoscience and Remote Sensing Symposium. Maryland，USA：the University of Maryland college Park，1990：2417-2422.

Suppression of Coherent Noise by Wavelet Combined with Bilateral Filtering in Digital Holography

XIAO Wen，WANG Qingwu，PAN Feng

( School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China )

Suppression of coherent noise in digital holography can obtain higher quality digital holographic reconstructed image. A suppression of holographic coherent noise method which combines bilateral filter and wavelet filter is proposed. Firstly, the holographic reconstructed image is decomposed by wavelet transformation. Then the high-frequency component in wavelet domain is suppressed by the wavelet shrinkage algorithm. The low-pass approximation component is filtered by the bilateral filter. Finally, the inverse wavelet transform is processed. Through the simulation analysis, this method improves the image peak signal-to-noise ratio 0.4 dB~2 dB, and got a higher correlation coefficientcloser with the original image. The method is verified by holographic experiment data,and the results show that this method can effectively suppress the speckle noise, and at the same time, retain more details information of the reconstructed image.

digital holographic; coherent noise; speckle suppression; wavelet transform; bilateral filtering

1003-501X(2016)08-0039-08

TN26

A

10.3969/j.issn.1003-501X.2016.08.007

2015-12-04；

2016-01-27

国家自然科学基金资助项目(61177006)

肖文(1962-)，男(汉族)，陕西西安人。教授，博士，主要研究方向为数字全息三维成像及相干检测。E-mail: xiaow@buaa.edu.cn。

王庆伍(1985-)，男(汉族)，安徽芜湖人。硕士研究生，主要研究方向为数字全息成像优化。E-mail: wangqingwu8510@163.com。