TheoH方差在光学陀螺随机误差分析中的应用

李 明，张 黎



TheoH方差在光学陀螺随机误差分析中的应用

李 明，张 黎

( 东北林业大学 机电工程学院，哈尔滨 150040 )

针对用Allan方差方法进行随机误差分析时平均时间只能达到数据长度的一半，以致长相关时间下估计值的置信度较低的问题，本文提出运用高置信度的混合理论方差(TheoH方差)对光学陀螺进行分析。该方法结合光学陀螺的信号特征，通过改变混合点位置对偏差补偿函数进行改进，提高了估计准确度。运用多种方差估计算法对仿真信号以及光学陀螺实测数据进行分析。实验结果表明，TheoH方差辨识结果和实际的幂律谱噪声特性一致，且具有比Allan方差更高的估计精度。

光纤元件；光学陀螺；随机误差；TheoH方差；Allan方差

0 引 言

光学陀螺的性能指标主要包括：零偏与零偏稳定性、角随机游走系数、标度因数、动态测量范围、带宽、启动时间、预热时间等。其中零偏不稳定性、角度随机游走系数和标度因数是评价光学陀螺性能的关键性指标，它直接决定了光学陀螺的应用领域和精度等级，代表了陀螺研制生产单位的技术水平。Allan方差是一种从时域数据中分析振荡器频率稳定性的方法，能够对光学陀螺输出角速率中存在的各个噪声项(包含零偏不稳定性和角度随机游走)和整个噪声系统进行细致的表征和辨识[1]。

然而运用Allan方差进行噪声信号处理时，其平均时间只能达到数据总时间长度的一半，在长相关时间下，由于估计实际自由度的降低，导致估计值的置信度较差。针对传统Allan方差的不足，学者们提出了很多改进算法。文献[2]运用重叠Allan方差(Overlapping Allan Variance)对惯性传感器的随机误差进行分析，通过重叠采样形成所有可能的相关时间为的子序列，来最大限度的利用现有数据估计Allan方差，但该方法的相关时间依然只能是总时间长度的一半。文献[3]运用总方差法对光纤陀螺的随机误差特性进行了分析，该方法虽然增加了方差估计的自由度，但延伸后的数据并不能反映信号的真实情况[4]。Theo1(Theoretical Variance #1，也称#1理论方差)方差是模仿Allan方差的较新的统计方法，其相关时间可以达到3/4(为信号总持续时间)，具有更好的置信度，但Theo1方差是对Allan方差的有偏估计，因此需要对其做偏差修正[5]。文献[6]将Theo1方差用于光学陀螺长相关时间下随机误差分析，提取出了更多的陀螺噪声信息。TheoH方差是去除了Theo1方差与Allan方差之间偏差，再与Allan方差在不同相关时间上合成的较新的统计方法，尤其适合相关时间较长和多种噪声混合存在的情况，可以从相同的数据序列中最大程度获得统计信息[7]。文献[8]运用TheoH方差对光学陀螺的随机误差进行了分析，取得了较好的效果，不过该方法在短相关时间用经典Allan方差混合来绘制双对数曲线，如果换成交叠Allan方差的话，应该可以进一步提高随机误差系数估计值的置信度[9]。

在文献[8]的基础上，本文在TheoH方差的双对数曲线绘制过程中，用交叠Allan方差代替Allan方差进行混合，提高了中、短相关时间下参数的估计置信度；同时通过调整去除偏离函数中交接时间点的位置，使双对数曲线更加平滑，便于使用最小二乘法进行参数拟合。将改进方法用于仿真信号和对陀螺实测数据的分析，结果表明该方法在中、短相关时间下具有和交叠Allan方差相同的估计置信度，而且在长相关时间下能获得更多的随机误差信息，提高了光学陀螺随机误差的估计准确度。

1 Allan方差与TheoH方差原理

1.1 Allan方差和交叠Allan方差

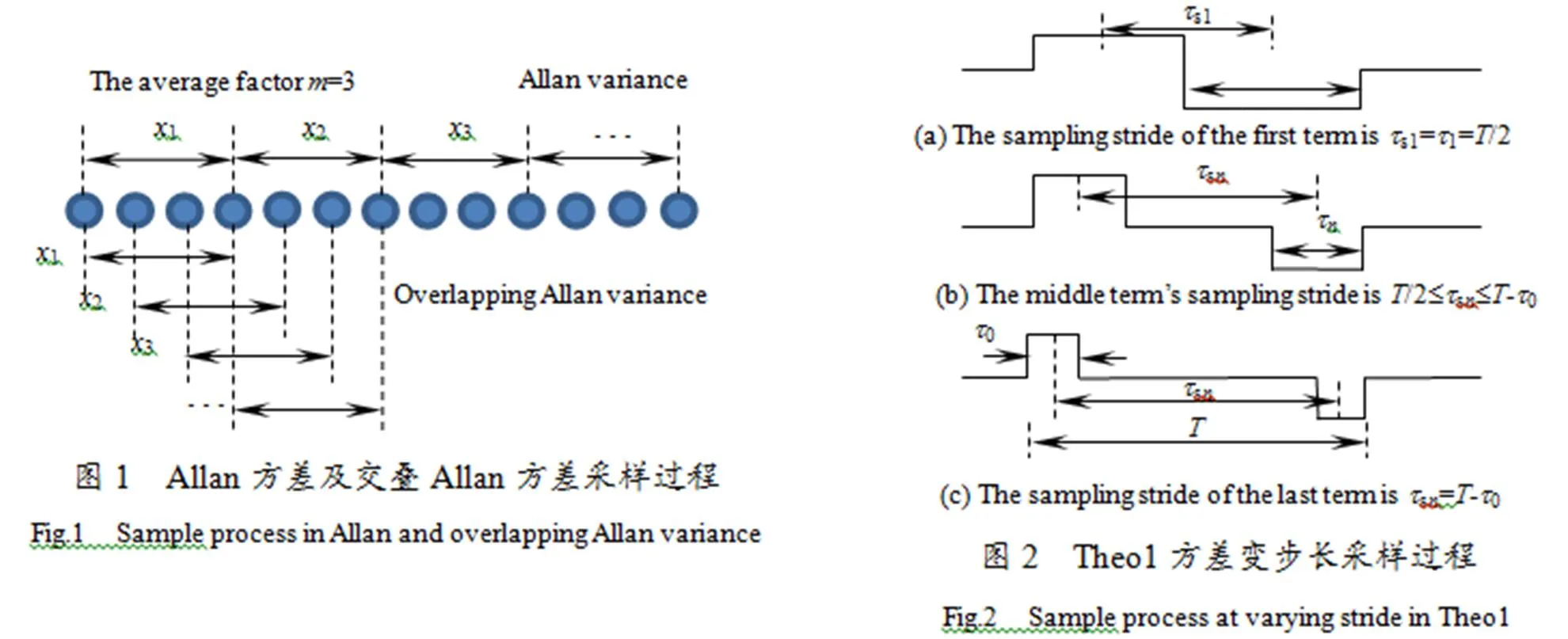
Allan方差是一种时域分析技术，本质是将光学陀螺输出的随机误差信号输入到带通参数(也称相关时间)的Allan方差滤波器，得到一组滤波输出，进而辨识和细化出较多的误差源。大量试验数据表明，不同的随机误差项将出现在不同的相关时间区域[8]。Allan方差的估计是基于有限长度数据，其估计的可信度完全依赖于数据的独立组数[6]。对于独立组数为的序列，代表Allan方差估计的实际自由度，对于随机信号来说，估计值的可信度随的增加而提高，Allan方差估计值的百分比误差为

为提高Allan方差的估计置信度，学者们又提出了交叠Allan方差，其采样示意图如图1。该方法除进行重叠采样外与Allan方差计算方法完全一样，可以有效提高Allan方差在短相关时间下的估计置信度，但由于其最大相关时间也为，所以在长相关时间下的估计置信度仍然不高。

1.2 Theo1方差和原理

Theo1方差是美国国家标准局(NIST)推荐的的一种新的方差分析方法，它具有和Allan方差相似的统计特性，但是在估计长相关时间下振荡器稳定性方面具有显著的优点，首先是计算的相关时间能达到数据总时间长度的75%，其次是具有更高的估计置信度，而且可以辨识出更多种类的噪声[10]。相比较于Allan方差，Theo1是一种估计性能提高了的方差分析方法，对于时间序列，采样间隔为，总时间为，Theo1方差采取了二次采样方法，就是在采样时间内，，为偶数，方差计算的采样时间步幅变为，再次进行采样。Theo1方差有两个采样时间，一个是，一个是，相对应于Allan方差的定义，Theo1方差的定义为

但是由于Theo1采用完全不同的数据采样方法，所以相对Allan方差是有偏的，因此需要对其做偏差修正。TheoBR(Bias-Removed version of Theo1，用表示)就是自动补偿Theo1与交叠Allan方差之间偏差后得到的方差计算函数。即：

为更准确的对随机误差进行估计，TheoH方差采用了一种混合统计的方式：

图3 交叠Allan方差与TheoBR方差组合过程

但是该算法在对光学陀螺进行分析时，会出现融合点重叠的问题，因此经过反复试验，本文提出将该算法的值变为条件下的最大值，这样能够使融合曲线更为平滑，更易于利用最小二乘法进行辨识，更适合光学陀螺的特点。相对于Allan方差，Theo1和TheoH理论方差估计置信度更高[5-8]。

2 仿真与实验研究

类似于Allan方差，TheoH方差能够很好地给出原子钟的频率稳定性。更为一般地，对于光学陀螺中的各种噪声，TheoH方差可以通过分析双对数图中对应的曲线斜率检验噪声类型以及辨识噪声参数。光学陀螺的随机误差源主要包括角度随机游走、偏置不稳定性、速率随机游走、速率斜坡、量化噪声，以及指数相关(Markov过程)噪声等[11]。这些随机噪声过程都可以用幂律谱模型来表征。因此，如果TheoH方差的分析对象是光学陀螺的角度信号或者角速度信号，TheoH方差分析方法完全可以替代Allan方差用于光学陀螺的随机误差特性分析，文献[6]和[8]证明了该推论。

2.1 仿真试验研究

光学陀螺中的随机噪声服从幂律谱噪声特性，通过改变与白噪声方差(或标准差)相关的参数，可以得到方差时变的各种幂律谱噪声[6]。文献[12]用一阶马尔可夫过程来模拟零偏不稳定性，用高斯白噪声驱动的数学模型来模拟其它噪声，作为光学陀螺仿真数学模型。本文借鉴该数学模型，采样频率为10 Hz，采样时间1200 s，仿真信号如图4。图中白色部分为零偏不稳定性，黑色部分为其它噪声项。本文重点只对零偏不稳定性进行提取是因为零偏不稳定是评价光学陀螺性能的重要指标，也是补偿算法和滤波算法中经常要用到的参数，因此本文着重考察多种算法在提取零偏不稳定性方面的表现。而评价光学陀螺的另一个指标——角度随机游走，是短相关时间下可以提取到的随机误差系数，用TheoH方差和Allan方差提取的结果相差不大，因此没有进行仿真。

图5是分别运用Allan方差、Theo1方差和TheoH方差对仿真信号进行分析的双对数曲线图，横轴为平均时间(或相关时间)，纵轴为标准差(Deviation，即方差的开平方)。从图中可以看出，当平均因子较小(即相关时间较短)时，传统Allan方差和TheoH方差几乎完全相等，但是在大的平均因子的情况下，由于传统Allan方差估计的自由度很小，估计值波动较大，尤其是在接近测量数据总持续时间的一半()时，Allan方差估计值波动非常剧烈，这是因为从对应的自由度来看，当时，Allan方差仅有一个自由度，而TheoH方差有2.1～6个自由度的原因[7]。图中还可以看到TheoH方差和Theo1方差的相关时间可以达到900 s左右且依然保持稳定，而Allan方差不到400 s就开始剧烈波动了。而且Theo1方差法在长相关时间下，由于没有得到有效补偿相对Allan方差发生了偏离，只有TheoH方差即通过改变采样步长进行二次采样的方法将相关时间提高到了，又对算法造成的偏离进行了自动补偿，为准确的辨识出陀螺的噪声系数提供了保障。

图6是文献[8]提出的Allan方差与TheoBR混合得到的TheoH方差(Hybrid of Allan and TheoBRVariance)，本文提出的交叠Allan方差与TheoBR混合得到的TheoH方差(Hybrid of Overlapping Allan and TheoBR Variance)和去除交接点跳变的改进的TheoH方差(Improvement TheoH Variance)三种方法的比较图。可以看到改进前不管是Allan方差还是重叠Allan方差同TheoBR方差并没有完全融合在一起，出现了一段突然的跳变，造成曲线不够平滑，必然会影响到下一步独立噪声项的辨识准确度。产生这个问题的原因是TheoBR方差的补偿函数是针对原子时钟频率稳定度的，并不完全适用于光学陀螺，本文通过大量试验对其算法进行了改动，将融合点由提前到了。使两种算法的融合更为完美，拟合出的曲线更为平滑，提高了辨识精度，更易于用最小二乘法等随机误差辨识方法进行拟合及噪声系数的提取。

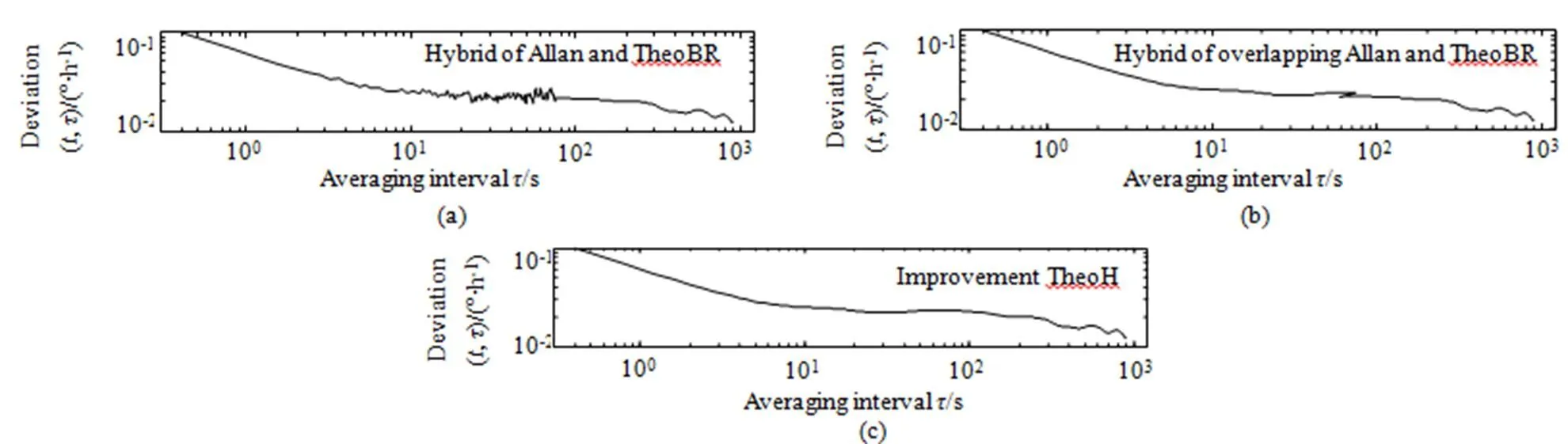
图6 TheoH方差改进前后双对数曲线比较图

把用一阶马尔可夫过程仿真的零偏不稳定性1 200 s平均值作为标准值(0.033 8)，分别用Allan方差、文献[8]提出的方法、本文提出的两种改进方法和来提取零偏不稳定性误差系数值，通过比较哪个更接近标准值来判断各个算法的参数辨识能力，比较结果见表1。可以看到，本文改进算法辨识出的零偏不稳定性估计值最接近标准值。

Table 1 Extraction results of bias instability by different variance analysis methods

2.2 光学陀螺信号随机误差分析

光学陀螺在工作时，受温度、辐射和外界环境干扰的综合影响，随机噪声较大，通过对陀螺的随机误差项进行辨识和细化，可以为进一步进行结构改进和算法补偿提供依据。本文以动态试验中采集到的陀螺输出信号为例，对多种方差分析算法进行了比较分析。图7为光纤陀螺的量测信号，采样时间间隔为0.05 s，采集数据约60 000个。

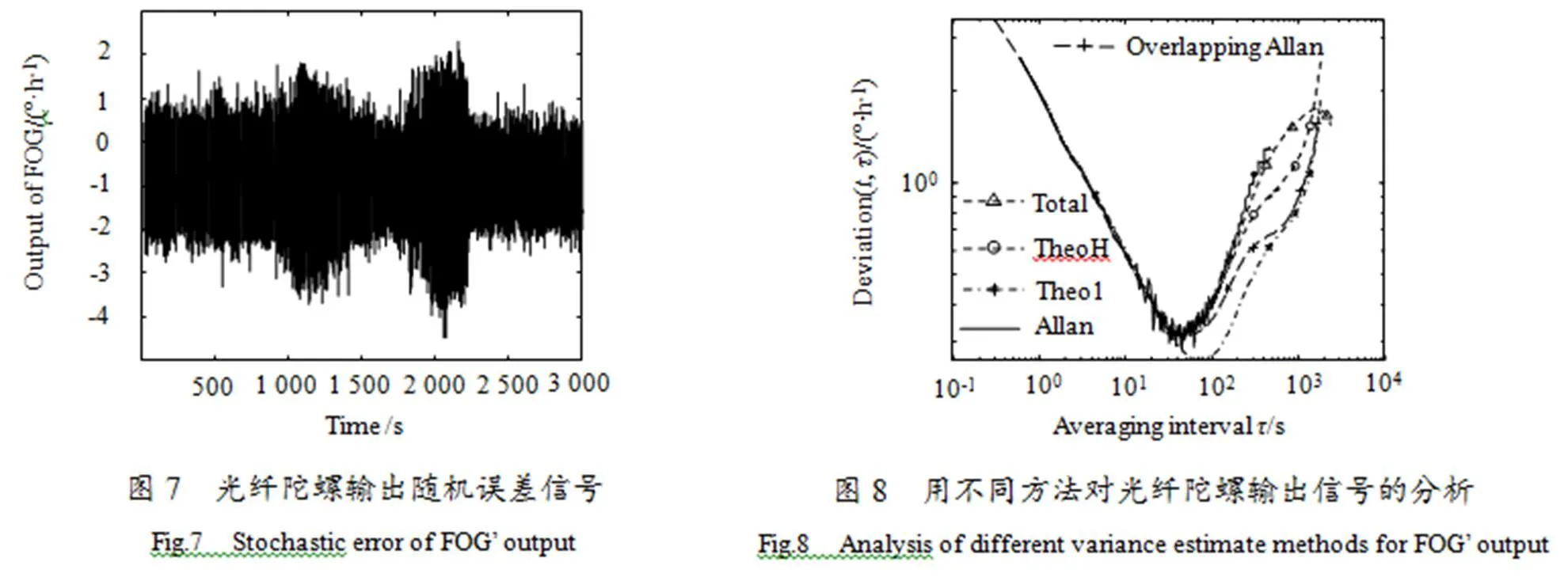
图8是用不同方差分析方法对光学陀螺启动信号进行分析的比较图。可以看到在短相关时间下各个方差的计算结果基本保持一致，在长相关时间下却完全不同：Allan方差的波动很大，交叠Allan方差虽然在短相关时间具有较高的置信度，但最多只能计算到数据总长度的一半，所以更长的相关时间还需要TheoH方差来进行估计，Theo1方差很早就偏离了方差变化的趋势，总方差的表现也正如它的数据延伸算法原理一样，延伸的数据不能代表信号真实变化，只是减小了波动，延续了短相关时间下变化的趋势，并不能真正的表征长相关时间下的变化特点。只有TheoH方差既能在短相关时间与Allan方差保持一致，又在其无法进行计算的长相关时间下进行了置信度较高的估计，二次采样的算法使之能包含更多的陀螺噪声信息，可以更为准确的提取出各个噪声项。

3 结 论

本文结合光学陀螺的特点，对用于原子时钟频率稳定度分析的TheoH方差进行了有效改进，使之更为适用于光学陀螺信号分析。该方法克服Allan方差方法在长相关时间下等效自由度低导致置信度低的问题，拟合出的方差曲线相关时间提高了50%，并且包含更多的噪声信息，为准确辨识和提取噪声源，并进一步对光学陀螺进行结构改进或导航滤波算法精度的提高提供了参考。

[1] 石国祥，陈坚，叶军，等. 总方差方法在光纤陀螺随机误差分析中的应用 [J]. 光电工程，2012，39(1)：62-67.

SHI Guoxiang，CHEN Jian，YE Jun，. Applications of total variance method in random error analysis of the fiber optic gyro signal [J]. Opto-Electronic Engineering，2012，39(1)：62-67.

[2] LI Jintao，FANG Jiancheng. Not fully overlapping Allan variance and total variance for inertial sensor stochastic error analysis [J]. IEEE Transactions on Instrumentation and Measurement(S0018-9456)，2013，62(10)：2659-2672.

[3] 韩军良，葛升民，沈毅. 基于总方差方法的光纤陀螺随机误差特性研究 [J]. 哈尔滨工业大学学报，2007，39(5)：708-711.

HAN Junliang，GE Shengmin，SHEN Yi. Research on the random error properties of FOG based on total variance [J]. Journal of Harbin Institute of Technology，2007，39(5)：708-711.

[4] Howe David A. The total deviation approach to long-term characterization of frequency stability [J]. IEEE Transactions on Ultrasonic，Ferroelectrics，and Frequency Control(S0885-3010)，2000，47(5)：1102-1110.

[5] Howe David A，Tasset T N. Theol： characterization of very long-term frequency stability [C]// Proceedings of the 18th European Frequency and Time Forum (EFTF '04)，Guildford，UK，April 5-7，2004：581-587.

[6] 程旭维，汤霞清，黄湘远. 基于#1理论方差的光学陀螺长期随机误差分析 [J]. 中国激光，2014，41(10)：10005003.1-10005003.8.

CHENG Xuwei，TANG Xiaqing，HUANG Xiangyuan. Investigation on random error properties of optic gyroscope based on Theoretical Variance #1 [J]. Chinese Journal of Lasers，2014，41(10)：10005003.1-10005003.8.

[7] Howe David A. TheoH：A hybrid，high-confidence statistic that improves on the Allan deviation [J]. Metrologia(S0026-1394)，2006，43(4)：322-331.

[8] 汤霞清，程旭维，高军强. 光学陀螺随机误差特性的混合理论方差方法分析 [J]. 兵工学报，2015，36(9)：1688-1695.
TANG Xiaqing，CHENG Xuwei，GAO Junqiang. Hybrid Theoretical Variance Analysis for Random Error Properties of Optic Gyroscope [J]. Acta Armamentaria，2015，36(9)：1688-1695.

[9] 李晓莹，胡敏，张鹏，等. 交叠式Allan方差在微机械陀螺随机误差辨识中的应用 [J]. 西北工业大学学报，2007，25(2)：225-229.
LI Xiaoying，HU Min，ZHANG Peng，. Applying Overlapping Allan Variance Theory to Better Stochastic Modeling of Microgyro [J]. Journal of Northwestern Polytechnical University，2007，25(2)：225-229.

[10] Levine Judah，Parker T. The algorithm used to realize UTC(NIST) [C]// 2002 IEEE International Frequency Control Symposium，New Orleans，Louisiana，USA，May 29-31，2002：537-542.

[11] 金毅，吴训忠，谢聂，等. 光纤陀螺随机漂移在线建模实时滤波技术 [J]. 光电工程，2015，42(3)：13-19.
JIN Yi，WU Xunzhong，XIE Nie，. Real-time Filtering Research Based on On-line Modeling Random Drift of FOG [J]. Opto-Electronic Engineering，2015，42(3)：13-19.

[12] 金毅，吴训忠，谢聂. 基于Allan方差的光纤陀螺随机漂移建模与仿真 [J]. 应用光学，2014，35(3)：547-551.
JIN Yi，WU Xunzhong，XIE Nie. Modeling and simulation of FOG random drift based on Allan variance [J]. Journal of Applied Optics，2014，35(3)：547-551.

Application of TheoH Variance in Stochastic Error Analysis for the Optical Gyroscope Signal

LI Ming，ZHANG Li

( College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China )

To solve the problems that the averaging time of Allan variance can only reach half of total data length，and confidence at long averaging time is lower, according to the random errors properties of the inertial sensors at time and frequency domains, a new method for analyzing the random error properties of the inertial sensor based on high confidence and hybrid Allan variance (TheoH variance) is proposed, which can better adapt to the characteristics of optical gyroscope by changing the location of the transition point. The simulated random error of optical gyroscope and measured data of FOG start-up signal are analyzed with the TheoH variance and other variance analysis method. The results show that the estimation values of the TheoH variance are consistent with power-law noise，It can efficiently improve the confidence in the case of great averaging time, and its estimation accuracy is higher than the Allan variance, especially in long term- values.

optical fiber components; optical gyroscope; stochastic error; TheoH variance; Allan variance

1003-501X(2016)08-0027-06

TN253

A

10.3969/j.issn.1003-501X.2016.08.005

2015-11-18；

2016-01-06

中央高校基本科研业务费专项资金项目(2572015BB06)；东北林业大学教育教学研究项目(DGY2014-33)

李明(1980-)，男(汉族)，江苏宿迁人。讲师，硕士，主要研究方向是计算机应用。E-mail: liming_nefu1980@sina.com。