中澳标准顺风向风载作用比较
刘天英,卢 昊,李孝启
(东北电力设计院有限公司,吉林 长春 130021)
中澳标准顺风向风载作用比较
刘天英,卢 昊,李孝启
(东北电力设计院有限公司,吉林 长春 130021)
为方便中国工程师与澳大利亚咨询工程师沟通,了解澳大利亚标准顺风向风载计算,本文对中国标准GB 50009-2012《建筑结构荷载规范》及澳大利亚标准AS/NZS 1170.2:2011《结构设计荷载 第2部分:风载》两部标准中顺风向风载计算进行介绍。对比研究顺风向风压系数如体型系数、风压高度变化系数、风振系数,并进一步探讨中澳标准间各系数的区别。通过具体算例比较中澳标准风载的大小,结果表明对于同一场地刚性建筑,基于澳大利亚标准的风载要高于基于中国标准的风载;对于风敏柔性建筑,从地面起澳标风载高于中标风载,随着高度增加,中澳标准风载差距在减小,当建筑达到一定高度时,中标风载在某个高度可能会超过澳标。
中澳标准;顺风向;风载作用。
中国工程公司在非洲及东南亚一带的国家和地区执行了很多电厂项目,项目大多采用EPC模式,由中国工程公司总承包。项目设计基于中国标准(以下简称中标),由中国设计公司完成,但图纸确认工作由这些国家或地区聘请发达国家的咨询工程师进行。澳大利亚咨询工程师在项目中经常遇到。澳大利亚咨询工程师熟知澳大利亚标准(以下简称澳标),不了解中标,中国工程设计人员正好相反。上述原因阻碍图纸的确认工作,为便于交流并顺利执行项目,了解澳标非常必要。风载为作用在建(构)筑物上的基本荷载之一,常控制建(构)筑物的安全。中国工程师应注意涉外项目风载参数常源于不同标准体系,如取值不当,结构可能存在安全隐患或经济性较差问题。风载进一步细分为顺风向风载(平行于风向)、横风向风载(垂直于风向)和扭转风载。顺风向风载在结构设计中最常遇到,所以有必要对中澳标准顺风向风载的计算进行对比,找出差异并分析对结果的影响。
1 顺风向风压
计算主要受力结构时,中标给出顺风向风载标准值:

式中:βz为高度z处的风振系数;μs为风荷载体型系数;μz为风压高度变化系数;ω0为基本风压(kN/m2)。
基本风压:
式中:ρ为空气密度,取1.25kg/m3;ν0为基本风速(m/s)。
进一步推导


从公式中可以看出,中标考虑地面粗糙度、建筑体型以及建筑自身动力特性对风载计算的影响。
澳标中给出建(构)筑物设计风压公式
式中:ρair为空气密度,取1.2 kg/m3;Vdes,θ为建筑主轴设计风速;Cfig为气动体型系数;Cdyn为动力响应系数。其中Vdes,θ的取值与场地风速Vsit,β有关,等于场地风速Vsit,β在β=θ±45°范围的最大值,风向β与建筑物主轴方向关系见图1。


式中:VR为区域风速(m/s);Md为方向系数;Mz,ca为场地高度系数;Ms为遮挡系数;Mt为特殊地形系数。
澳标分A、W、B、C、D共5个风压区,方向系数Md随风压分区不同取值不同。对于A及W区,
8个主要方向的Md取值在0.8~1.0之间,详见澳标表3.2。对于B、C、D区,当确定作用在整个建筑的合力及倾覆弯矩和主要结构构件的风载时,Md取0.95;其他情况(包括墙板及中间支撑构件),Md取1.0。假定8个主要方向场地风速Vsit,β见图2,建筑主轴设计风速:

亦即取x位置的Vsit,β值,该处Md通过插值获得。

图1 风向β与建筑物主轴方向关系

澳标大部分情况下Ms及Mt可取1.0,具体取值详见下文。则进一步推导

从中澳标准计算风压公式中可以看出,前面的数值系数差值很小,主要由于采用的空气密度不同所致。中标没有方向系数概念,澳标方向系数Md可做为数值系数处理。虽然其他系数在表达形式有一定区别,但从定义上看各系数之间有大致对应关系,详见表1。

表1 风压系数对应关系
2 基本风压
从中标基本风压定义可以推出基本风速V0定义为当地空旷平坦地面(标准中地面粗糙度B类)上10 m高度处50年一遇10 min内的平均最大风速。澳标区域风速VR相当于中标基本风速,但定义与中标不同,为当地空旷平坦地面(标准中地面粗糙度2类)上10 m高度处3 s内的平均最大风速,重现期根据建筑重要性等级可选。
中标规定,对于高层建筑、高耸结构以及对风荷载比较敏感的其他结构,基本风压的取值应适当提高,承载力设计时可按基本风压的1.1倍采用,但并没提及重要性等级。澳标根据建(构)筑物破坏对人的生命及财产的危害程度将建(构)筑物重要性分为四类,详见表2。根据不同重要性等级,取不同重现期R(年超越概率的倒数)的区域风速VR,重现期及年超越概率取值见表3。

表2 建(构)筑物重要性等级

表3 风速年超概率及重现期
从中澳两个标准基本风速定义上,可以看出有两处区别,分别为重现期及时距不同。重现期中国取50年,而澳大利亚重现期根据建筑物重要性等级不同取值不同。时距中国取10 min,而澳大利亚取3 s。根据相关文献,风载参数的取值虽然不同,但可以进行换算。关于时距的换算见表4。从表4可以看出,澳大利亚基本风速V3S与中国基本风速V10 min关系为V3s=1.42V10 min。

表4 不同时距与10 min时距平均风速的换算系数
对于不同重现期间基本风速换算,欧洲钢结构协会规定了风速重现期换算系数进行计算,欧洲钢结构协会规定的换算系数是以重现期为50年的风速为基准,其表达式为:
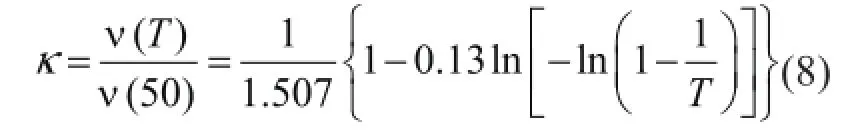
式中:T为重现期,υ(50)为50年重现期风速。
例如对于澳标位于B区的2类建筑物,重现期R取500年,澳大利亚区域风速V500与中国基本风速ν0的关系为V500=1.20ν0。那么最终澳大利亚区域风速VR=(1.20×1.42)ν0= 1.704ν0,可见对于B区2类建筑物,澳标基本风速为中标基本风速值1.704倍,对于另外的建筑物,此值在变化。
3 基本风压系数
3.1风压高度变化系数
在大气边界层内,风速随离地面高度增加而增大。当气压场随高度不变时,风速随高度增大的规律,主要取决于地面粗糙度。在这一点上,中标和澳标相同。中标采用风压高度变化系数μz来体现风压的变化,实际上是体现风速变化。澳标采用场地高度系数Mz,cat来体现地形不同对风速的影响,转换到风压时,应为平方关系。
中标地面粗糙度细分为A、B、C、D四类,详细描述见中标8.2.1款。为便于应用,中标风压高度变化系数取值列于GB 50009表8.2.1,可直接查阅。需要说明的是中标在确定城区地面粗糙度类别时,以拟建房2 km为半径的迎风半圆影响范围内的房屋高度和密集度来区分粗糙度类别,风向原则上以该地区最大风的风向为准,也可取其主导风。以半圆影响范围内建筑物的平均高度ha划分地面粗糙度类别,当ha≥18 m,为D类;9 m<ha<18 m,为C类;ha≤9 m,为B类。澳标将地形种类同样分为四类。类别1:没有或几乎没有障碍物的暴露开阔地面及正常使用风速的水面。类别2:水面、开阔地面、有少数很分散的1.5 m到10 m高障碍物的草地。类别3:许多近距离的3.0 m到5.0 m高障碍物的地形,如城郊住宅区域。类别4:有很多大、高(10.0 m到30.0 m)和近距离障碍物地形,如大城市中心、开发很好的工业区。从两本规范的描述上看,地形类别数量均为四类。从描述上中标A类包含澳标的1类及部分2类。中澳标准地形类别大致的对应关系,见表5。

表5 中澳标准地形类别对比
为便于取用,中标规风压高度变化系数μz的取值详见GB 50009中表8.2.1。澳标风压A、W、B区高度变化系数Mz,cat取值详见表6,风压C、D区高度变化系数Mz,cat取值详见表7。
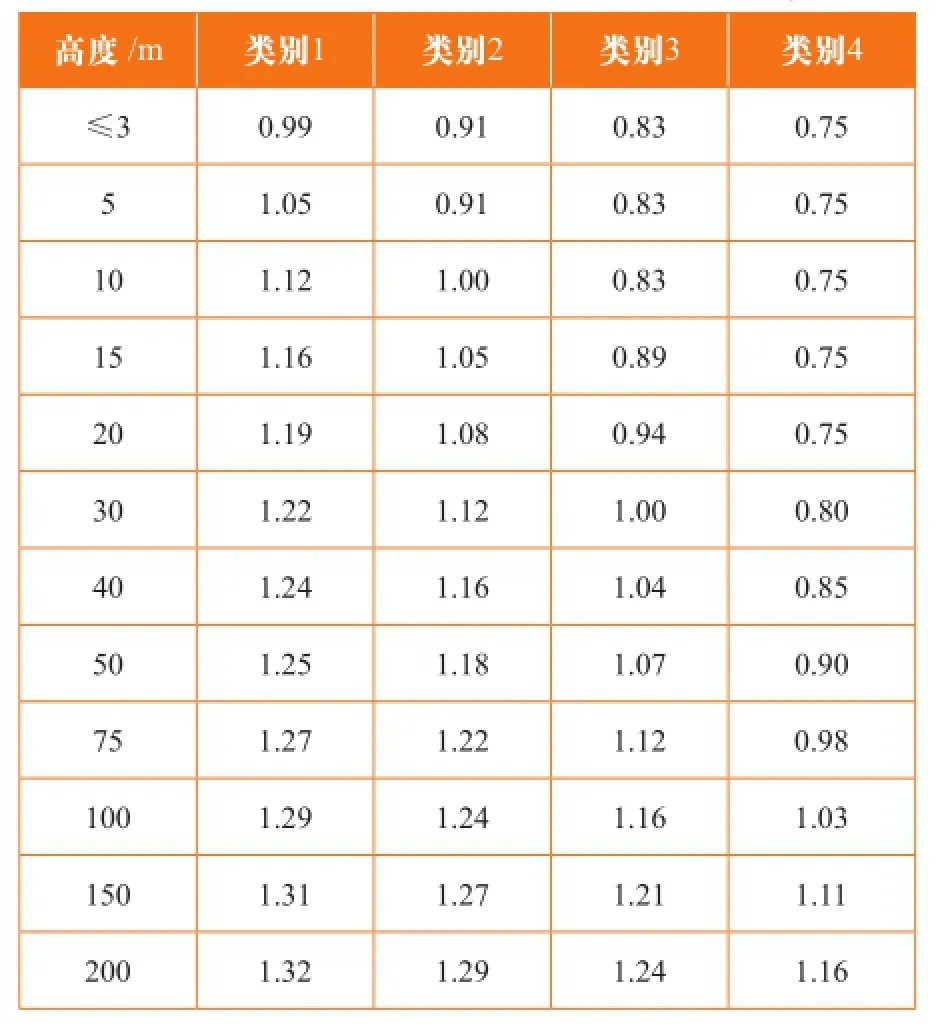
表6 A、W、B区场地高度变化系数Mz,cat
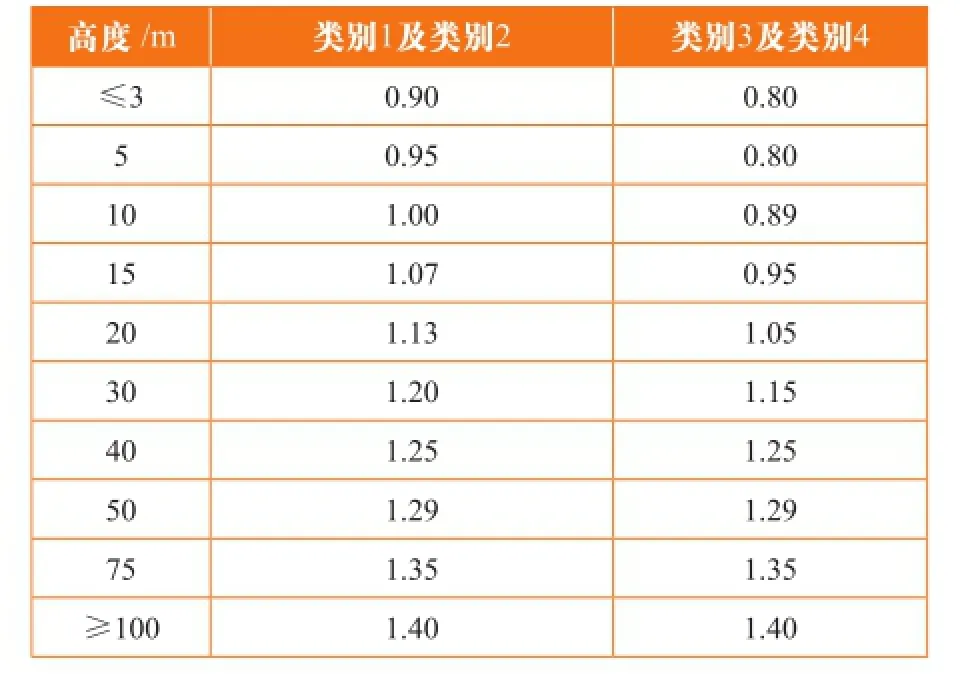
表7 C、D区场地高度变化系数Mz,cat
可见澳标中不同风压分区,对于不同的地形类别,场地高度变化系数也是不同的,中标没有澳标细致。同一地形类别中,中标不同高度处风压高度变化系数与10 m处风压高度变化系数的比值要高于澳标,也就是说,中标风速随高度的变化要快于澳标。
3.2体型系数
风荷载体型系数通过风洞试验或在建筑物上实测得到,是用来反映作用在建筑表面上实际压力与速度压的比值关系,有的国家称为压力系数、气动体型系数、力系数、空气动力系数等。该系数主要与建筑物的体型和尺寸有关,因此中标称为风荷载体型系数,实际就是面上的加权平均压力系数。中标表8.3.1中详细列出不同类型的建(构)筑物体型及其体型系数μs。对于常规矩形建筑物的体型系数,迎风面为+ 0.8,为压力,背风面-0.5,为吸力。对于超过45 m的矩形截面建筑物的体型系数,还与矩形的长宽比有关。迎风面一直为0.8,但背风面体型系数随长宽比(D/B)变化而变化,宽度指迎风面的宽度。当D/B≤1,取-0.6;D/B=1.2时,取-0.5;D/B=2时,取-0.4;D/B≥4,取-0.3 。中间值进行内插。
与中标风荷载体型系数对应的是澳标的气动体型系数Cfig,主要与建筑物的体型和尺寸有关。对于封闭建筑物
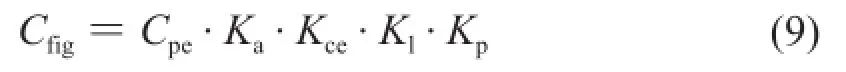
式中:Cpe为外部压力系数;Ka为面积折减系数;Kce为外部压力组合系数;Kl为局部压力系数;Kp为孔隙墙板折减系数。
当计算主体结构受力时,Ka、Kl、Kp均可取1.0,Kce对于迎风面墙和背风面墙2个有效表面同时作用时取0.9,详见澳标5.4节。对于矩形封闭建筑,当房屋高度h>25m时,风速随高度变化时,迎风面墙Cpe取0.8。当房屋高度h≤25m时,当风速随高度变化时,迎风面墙Cpe取0.8;当风速取建筑最高点h处值时,迎风面墙Cpe取0.7。矩形封闭建筑背风面压力系数Cpe详见表8。
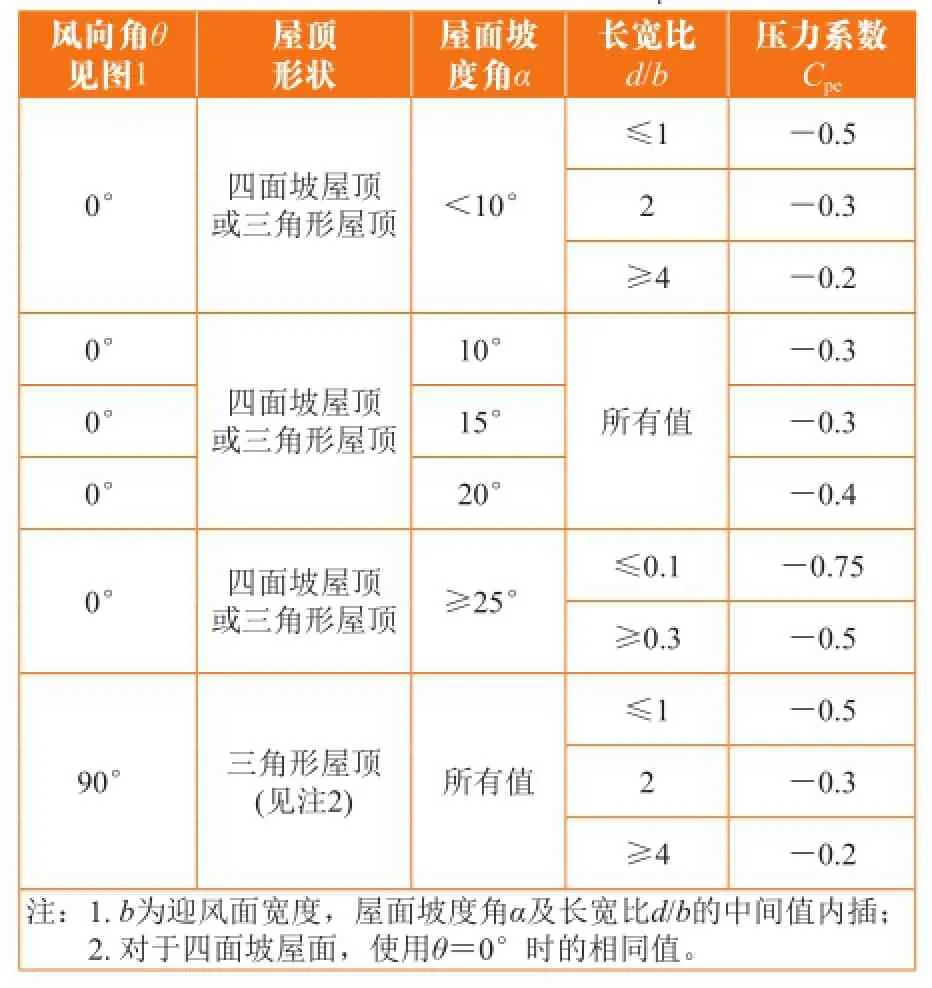
表8 背风面压力系数Cpe
从表8中可以看出,澳标压力系数Cp,e值随建筑高度、风速取值、长宽比(a/b)及屋面坡度角α的变化而变化,考虑的因素较多。而中标迎风面的体型系数始终为0.8,背风面仅考虑建筑长宽比的因素,值相对比澳标大。
3.3风振系数
中标对于高度大于30 m且高宽比大于1.5的房屋,以及基本自振周期T1大于0.25 s的各种高耸结构考虑风振系数影响。对于主要受力结构,中标风荷载标准值的表达采用平均风压乘以风振系数βz。中标z高度处的风振系数:
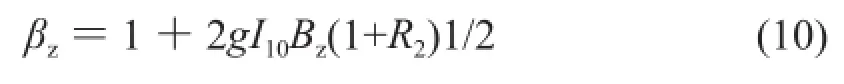
式中:g为峰值因子,取2.5;I10为10 m高度名义湍流强度,对应A、B、C和D类地面粗糙度,分别取0.12、0.14、0.23和0.39; R为脉动风荷载的共振分量因子;Bz为脉动风荷载的背景分量因子。风振系数的计算按中标第8.4节的相关规定进行。
澳标当建筑物或其单元第一振型的自振频率na大于1.0 Hz,动力响应系数Cdyn=1.0。对高层建筑及自立式塔0.2 Hz≤na≤1.0 Hz,需要计算动力响应系数。对于悬挑屋面0.5 Hz≤na≤1.0 Hz,需要计算动力响应系数。其他情况,需要另外考虑,没有包含在AS/NZS 1170.2标准中。
动力响应系数:
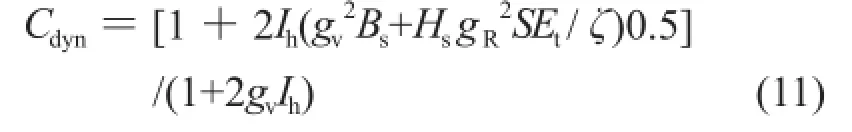
式中:s为建筑风载作用计算点高度;h为建筑总高;gv为上风向速度波动峰值系数,取3.7;Ih为湍流强度;Bs为背景系数;Hs为共振响应高度系数,取1+(s/h)2; S为尺寸折减系数;Et-π/4倍到来气流湍流谱;ζ为结构阻尼比;gR为共振响应峰值系数(10 min周期),gR=[2loge(600na)]0.5。动力响应系数的计算按澳标第6章的相关规定进行。
从公式上可以看出,中澳标准考虑第一振型的随机振动理论推导得出的动力系数均大于1.0。中澳标准的公式都很复杂,均考虑了地形类别、背景系数以及共振系数等因素的影响,但公式表现形式不同。
4 算例
算例一某封闭建筑,钢筋混凝土框架结构。平面尺寸为20 m×20 m,总高度为20 m,平屋面。共6层,每层高约3.33 m。位于澳标风压分区W区,粗糙度类别2类,建筑重要性等级为2级,重现期500年基本风速为51 m/s。方向系数Md取0.95,第一振型自振频率na为3.3 Hz。相应中标风载参数,粗糙度类别为B类,基本风速为30 m/s。根据相关条款,中标风振系数βz=1.0,澳标动力响应系数Cdyn=1.0。为便于计算,将总高20 m分为两段,下部10 m及上部10 m。基于中澳标准的风荷载计算对比详见表9。

表9 中澳风荷载计算对比
算例二某钢结构框架,设钢支撑,金属墙板围护。平面尺寸为30 m×30 m,层高3.33 m,共30层,总高度为100 m,平屋面。澳标风载参数:位于澳标风压分区W区,粗糙度类别2类,建筑重要性等级为3级,重现期1000年基本风速为53 m/s。方向系数Md取0.95,第一振型自振频率na为0.27 Hz。相应的中标参数:地面粗糙度类别B类,基本风速为31.1 m/s,结构的基本自振周期3.75 s。该建筑为风敏高层,考虑1.1倍系数,中标ω0=0.66 kN/m2,澳标基于中澳标准的风荷载计算对比详见表10,计算过程略。根据中澳标准的相关条款,需考虑动力系数,各分段点动力系数的对比见图3,各分段点处风载值对比见图4。为便于对比,图中均取为10 m一段。

图3 动力系数对比
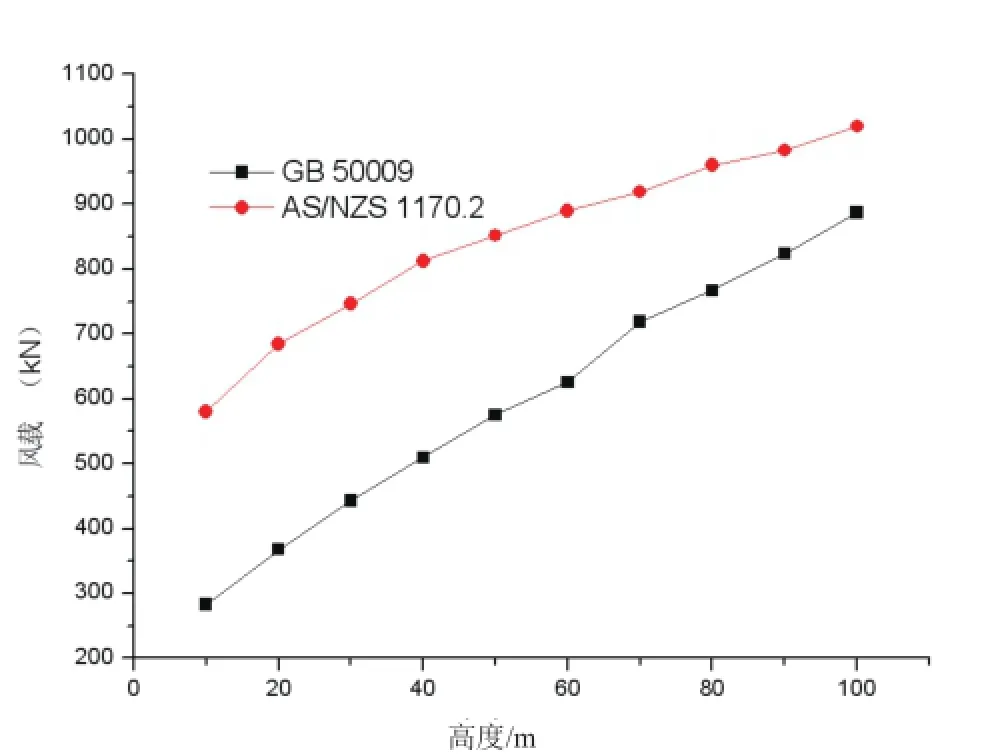
图4 风载对比
5 结论
根据文中对比研究,得出如下结论:
同一场地,中澳标准基本风速数值不同,因为中澳基本风速时距及重现期不同。中标基本风速时距为10 min,而澳标时距为3s。中标基本风速重现期取50年,而澳标重现期根据建筑重要性等级不同取值不同。
对于刚性建筑,基于澳标的风载值高于基于中标的风载值,主要原因是澳标计算刚性建筑时采用3 s基本风速,并且重现期也高于中标,该基本风速值远大于中标的基本风速值。
对于柔性建筑,澳标的动力系数随高度增加比较缓慢。中标的动力系数随高度增加而快速增加。随着高度增加,中澳标准动力系数的差距在加大。
对于柔性建筑,从地面起澳标的风载要高于中标,随着高度增加,中澳风载间差距在减小,主要原因是风载动力系数及风压高度变化系数澳标随高度增加速度比中标慢。当建筑达到一定高度时,在某个高度中标风载可能超过澳标。
虽然澳标风载高于中标风载,但不可简单认为澳标安全度高于中标。承载力极限状态设计时中标风载分项系数1.4,澳标为1.0;另外还需对比抗力方面要求。
[1] GB 50009-2012,建筑结构荷载规范 [S].
[2] AS/NZS 1170.2:2011,Australian/New Zealand Standard Structural design actions Part 2:wind actions[S].
[3] AS/NZS 1170.0:2002,Australian/New Zealand Standard Structural design actions Part 0:general principles[S].
[4] National Construction Code Series 2015 volume one[M].Sydney: Australian Building Codes Board,2015.
[5] ASCE7-10, Minimum Design Loads for Buildings and Other Structures [S].
[6] JGJ 3-2010,高层建筑混凝土结构技术规程[S].
[7] 黄本才.结构抗风分析原理及应用[M].上海:同济大学出版社,2001.
[8]刘天英,齐秋平.中外规范基本风速对比分析[J].钢结构:2012,27(12).
[9] 黄韬颖,杨庆山.中美澳风荷载规范重要参数的比较[J].工程建设与设计,2007,(1).
Comparison on Wind Load Action in Along-wind Direction Between Chinese and Australian Code
LIU Tian-ying, LU Hao, LI Xiao-qi
(North-East Electric Power Design Institute Company Ltd., Changchun130021,China)
To exchange idea with Australian consultants conveniently for Chinese engineer and to know calculation about along-wind direction wind load action of Australian code, this paper introduces calculation about along-wind direction wind load action in Chinese code GB 50009-2012<Load code for the design of building structures〉 and Australian code AS/ NZS 1170.2:2011 <Structural design actions Part 2: Wind actions〉. The comparison and study are made about the factors of along-wind direction wind pressure such as shape factor, exposure factor and dynamic effect factor in Chinese and Australian code respectively, and the further discussion is made about difference of these factors. The wind load value is compared between Chinese and Australian code with examples, the result shows that wind load based on Australian code is higher than that based on Chinese code for stiff building in the same site;for wind-sensitive flexible building, wind load based on Australian code is higher than that based on Chinese code from ground level, the difference of wind load between Australian code and Chinese code is reduced gradually along height. When the height of building reaches some value, the wind load based on Chinese code will exceed that based on Australian code at somewhere.
Chinese and Australian code; along-wind direction; wind load action.
TM621
B
1671-9913(2016)04-0061-06
2015-06-08
刘天英(1975- ),男,吉林长春人,高级工程师,从事火力发电厂结构设计。

