配电网量测点优化布置研究
戴桂木 王萌萌 周 欣
(东南大学电气工程学院,南京 210096)
配电网量测点优化布置研究
戴桂木王萌萌周欣
(东南大学电气工程学院,南京210096)
针对配电网完全可观,提出了一种基于支路完全可观的配电网量测点优化布置算法。通过对配电网可观性的分析,建立了支路功率完全可观的配电网量测点优化布置基本模型,并且考虑了基本布置模型的改进,使得量测点的布置更加合理。通过对模型的求解,在37节点和69节点配电网系统中验证了所提算法的正确性。
配电网;可观性;量测点布置;优化算法
配电网的节点众多、支路复杂,一般呈辐射状结构。为了实现对配电网的有效监测,需要考虑一定的量测点布置,从而获取配电网中的实时量测量。有效准确的实时量测信息可以实现对配电网的全局可观测,并且通过计算得到配电网所有节点的状态信息,获取配电网的实时运行状态信息。由于配电网一般规模较大,在所有的节点处都布置量测装置既不合理也不经济,因此考虑在配电网中布置最少的量测点实现对整个配电网的可观测具有重要的意义。
关于网络可观测性的研究,在输电网里相角量测装置(Phasor Measurement Unit,PMU)得到了很大的应用[1-5]。文献[6]从潮流方程直接可解的方面,提出了一种PMU的优化布置方法,但是由于PMU的投资成本高昂,在配电网中大量布置PMU装置将十分不经济。文献[7-8]提出了配电网中的故障行波定位装置的最优配置算法。文献[9]运用启发式的网络分割方法,解决了配电网中的表计配置优化问题。文献[10]通过考虑在配电网中合理地增加量测种类和量测数量配置的方法来提高配电网的状态估计精度。文献[11]从可靠性和经济性双重约束方面,研究了配电网中馈线终端单元的优化配置问题。这些方法都对配电网中运用装置的优化配置情况展开了研究,但是从配电网网络可观性的角度考虑量测点的优化布置的现有研究还比较少。
本文在分析配电网可观性的基础上,针对辐射状结构的配电网提出了基于支路完全可观的配电网量测点优化布置方法。首先对支路功率可观实现配电网完全可观的原理进行了分析,然后基于支路完全可观的原理建立了配电网量测点优化布置的基本数学模型,以及结合配电网的实际情况,对基本布置模型进行改进,使得量测点的优化布置更加合理。最后在Matlab软件中运用分枝定界法对模型进行求解,在IEEE 37节点和美国PG&E 69节点配电网系统中验证了所提算法的正确性和合理性。
1 基于支路功率可观的配电网可观原理
对于一个N节点b条支路的辐射状结构配电网来说,如果网络中所有节点的电压的幅值和相角可以通过系统内的所有的实时量测量求解得到,则该配电网系统完全可观。从数值分析方法上看,即对于一个量测配电网,有如下量测方程:

式中,z为量测量矢量;H为雅克比矩阵;x为电压矢量;e为量测误差矢量。从代数上分析,如果矩阵H为满秩的,则可以求出所有节点的电压相量,因此配电网实现了完全可观。

图1 配电网馈线图
如果其中节点3是量测布置点,则支路l2的复功率和支路l3的复功率可以在量测布置节点3获取,根据基尔霍夫定律,可以得到如下支路方程:

由式(2)可知,对于一个含N个节点,b条支路的辐射状配电网,其中b=N−1,如果可以列出b个支路功率方程,由于已知,则通过可以通过联立b个支路功率方程求解得到所有节点的电压。因此,如果一个配电网中所有支路的功率可以通过所有布置的量测点获得,则所有节点的电压可以通过支路功率方程组求解得到,则配电网实现了完全可观。
因此,本文提出基于支路功率可观的配电网可观原理为:如果一个配电网中所有节点间相连的支路功率(有功和无功)完全可观,则配电网完全可观。
另外需要提及的是,本文中所提到的支路功率完全可观并没有强调是支路的首端还是末端量测得到的功率值,只要可以通过支路的一端可以量测得到支路功率值,即该支路可观测。只是在建立支路方程时,根据支路不同端量测得到的功率建立相应的支路方程即可。
2 基于支路可观的配电网量测点优化布置基本模型
通过上节的分析可知,对于配电网中的一个节点来说,如果该节点为量测布置点,则与该节点相连的所有支路的支路功率可以被全部量测得到。因此构建基于支路可观的配电网量测点布置基本数学模型如下:

式中,Ab×n为网络描述矩阵;b为支路数;n为节点数,描述矩阵中元素aij定义如下:

量测点布置矩阵 Xn×1=[x1,x2,…,xn]表示量测点布置矩阵,其中xi定义如下:

用支路完全可观矩阵Bb×1=[1,1,…,1]T表示配电网所有支路功率完全可观测。
由于变电站出线端一般会要求为量测点,因此将x1=1加入约束条件。
3 量测点优化布置的改进模型
首先引入支路可观度的概念,本文中定义支路可观度为:与支路相连的两个节点中包含的量测布置点的个数。由此可知,支路可观度di的取值只有0、1、2三种情况。
在配电网中,发生某条支路上的功率量测由于故障,而导致量测数据缺失的概率很大。因此为了保证在发生支路功率量测缺失情况下配电网依然能够被完全可观测,每条支路的可观度应当满足下式:

但是由于配电网中存在一定量的零注入节点,并不需要每条支路的可观度都满足式(7)条件,下面将分析与零注入节点相连的支路的可观度要求。
在配电网中,节点类型可以根据是否连接负荷分为两类:零注入节点和负荷节点。如图2所示,其中节点2为零注入节点(又称为虚拟量测点),节点1、3、4、5、6为负荷节点。以图2为例,节点2处的电流方程满足:
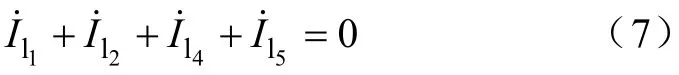

或者表示为


图2 配电网节点类型
由此可知,配电网中存在支路只与一个零注入节点相连时,支路的可观度只需要满足di≥1,即可保证在支路功率量测发生缺失时,配电网依然可观。
同时在配电网中也可能存在支路相连的两个节点都是零注入节点的情况,如图3所示。

图3 支路与2个零注入节点相连
其中,节点2和节点3都是零注入节点,并且通过支路l2相连。对于节点2和节点3来说,支路l2是互为冗余可观的。也就是说,支路l2的功率既可以由与零注入节点2相连的所有支路功率方程组和节点2的电流平衡方程计算得到,也可以由与零注入节点3相连的所有支路功率方程组和节点3的电流平衡方程计算得到。因此当其他支路(支路l1、l3、l4、l5、l6、l7)中一条支路功率量测缺失,都不影响支路l2的可观性。所以对于两个零注入节点之间支路,该条支路只需要满足可观度di≥0。
另外,对于辐射状配电网中的馈线末端节点,如果末端节点相连的支路功率发生缺失,馈线末端节点成为孤岛状态,对整体配电网的可观性影响不大,因此与末端节点相连的支路的可观度只需满足di≥1。
综上所述,考虑了配电网中某条支路量测发生缺失的一般情况,并且结合对配电网中零注入节点的分析,得到改进的量测点优化布置模型如下:
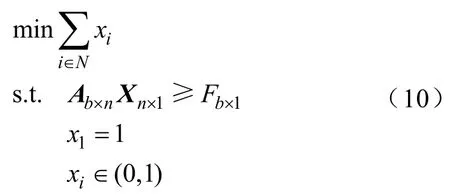
网络描述矩阵Ab×n和量测点布置矩阵Xn×n定义不变,改进模型下支路功率完全可观矩阵Fb×1定义为

4 实例分析
基于支路完全可观的量测点布置模型是属于一个0-1整数线性规划问题,整数规划问题的求解有很多方法,本文采用运用较多的分枝定界法求解该整数规划问题。在Matlab软件环境中对基本模型和改进的优化布置模型进行求解,并且在IEEE 37节点和美国PG&E 69节点配电网系统中验证了本文所提算法的正确性和有效性。
图4和图5为37节点和69节点配电网系统,其中节点1均为变电站出线端。根据本文所述算法,求解得到基本模型和改进模型的量测点布置结果见表1。

表1 量测点优化布置结果
从表1可以看出,在配电网系统中可以通过布置一定量的量测点获取整个配电网的所有支路功率,从而通过支路功率方程求解出所有的节点电压状态相量,实现整个配电网完全可观。对于37节点配电网系统,基本模型只需要布置15个量测点即可实现网络可观,而改进模型需要布置19个量测点;而在69节点配电网系统中,基本模型最少需要布置34个量测点才能实现完全可观,改进模型则需要41个量测布置点。因此,随着配电网规模的扩大,配电网需要布置的量测点的数量也随之增大。同时,对于同一个配电网系统,改进模型所需要布置的量测点数量虽然多于基本模型,但是两者数量相差并不是很大。因此相比于基本模型,改进模型考虑了配电网中一条支路功率量测发生故障缺失的情况,并且考虑了配电网中零注入节点的影响,使得改进模型的量测点优化布置更符合配电网的运行需求。
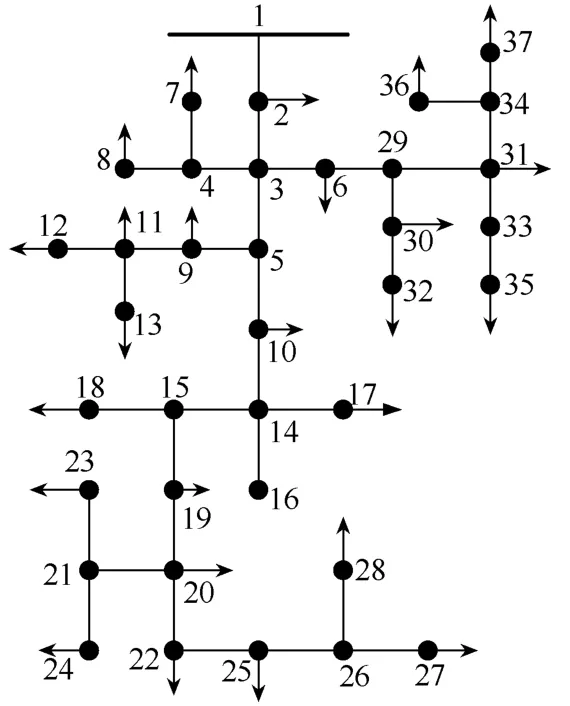
图4 37节点配电网系统拓扑图

图5 69节点配电网系统拓扑图
5 结论
配电网的完全可观对配电网的运行十分重要,为了获取配电网实时运行状态,需要通过在配电网中布置量测点从而实现对整个配电网的完全可观性需求。本文通过分析配电网可观性,提出了一种基于支路完全可观的配电网量测点布置方法。主要实现了以下目标。
1)基于支路可观原理建立配电网中量测点布置基本模型,实现了在配电网中布置最少的量测点,获取所有支路功率可以实现整个配电网的完全可观。
2)考虑配电网的实际运行情况,提出了量测点布置的改进模型,结合配电网中零注入节点对量测点布置的影响分析,考虑一条支路功率量测故障下的配电网的量测点优化布置。
3)通过37节点和69节点配电网算例分析可知,在配电网中只需要布置一定的量测点数量,即可实现整个配电网的完全可观。同时虽然改进模型比基本模型所需布置的量测点数量有所增加,但是改进模型的量测点布置更适应于配电网实际运行需求。
[1] 卫志农,孙国强,常宝立,等. 考虑电力系统潮流直接可解的同步相量量测单元最优配置[J]. 电网技术,2005,29(1)︰65-68.
[2] 罗毅,赵冬梅. 电力系统PMU最优配置数字规划算法[J]. 电力系统自动化,2006,30(9)︰20-24.
[3] 刘新东,江全元,曹一家. N−1条件下不失去可观测性的 PMU优化配置方法[J]. 中国电机工程学报,2009,29(10)︰47-51.
[4] 王家林,夏立,吴正国,等. 电力系统 PMU最优配置新方法[J]. 电力系统及其自动化学报,2011,23(6)︰1-5.
[5] 徐岩,郅静. 基于改进自适应遗传算法的PMU优化配置[J]. 电力系统保护与控制,2015,43(2)︰55-62.
[6] 邢洁,韩学山,武鹏. 使潮流方程直接可解的 PMU配置方法的改进[J]. 电网技术,2006,30(11)︰30-34.
[7] 李泽文,易志鹏,杨毅,等. 基于遗传算法的电网故障行波定位装置的优化配置[J]. 电力系统保护与控制,2015,43(3)︰77-83.
[8] 邓丰,陈楠,曾祥君,等. 基于图论的电网故障行波定位装置最优配置算法[J]. 电力系统自动化,2010,34(11)︰87-92.
[9] 陈得治,郭志忠. 基于表计配置的配电网可观测性分析[J]. 中国电机工程学报,2005,25(12)︰35-41.
[10] 高亚静,张占龙,吴文传,等. 配电网量测配置评估及优化[J]. 中国电力,2014,47(7)︰39-44.
[11] 徐飞. 配网自动化条件下的 FTU优化配置[J]. 四川电力技术,2013,36(2)︰48-53.
The Study of Optimal Measurement Placement in the Distribution Network
Dai GuimuWang MengmengZhou Xin
(School of Electrical Engineering,Southeast University,Nanjing210096)
An optimal measurement placement algorithm in the distribution network based on branch-observed is proposed in order to make the distribution network totally observable. Firstly,the observation of the distribution network is analyzed,and the basic optimal model of the measurement placement based on the branch-observed is established. Then an improved model is considered and the measurement placement is more practical. At last,the model has been solved and the correctness of the proposed algorithm has been verified in the 37-bus and 69-bus distribution network.
the distribution network; observability; measurement placement; optimal algorithm
戴桂木(1990-),男,硕士研究生,主要研究主动配电网与分布式发电。

