一种基于EPLL技术的自适应正交解调技术研究
王玉良,邢朝洋,郑旭东,曾青林
(北京航天控制仪器研究所,北京100039)
一种基于EPLL技术的自适应正交解调技术研究
王玉良,邢朝洋,郑旭东,曾青林
(北京航天控制仪器研究所,北京100039)
针对过零检测实现的全数字锁相环不仅锁相速度慢,而且过零点的扰动会直接影响锁相精度以及适合模拟电路实现的相干解调技术,在数字电路中实现则需要设计高阶数字低通滤波器,将占用大量数字电路资源并且会显著增加系统功耗等问题,在设计一种新型全数字锁相环(All-digital Enhanced Phase-lock Loop,EPLL)的基础上,结合自适应正交解调技术,提出了一种基于EPLL技术的自适应正交解调技术方案,并对该方案进行了研究与仿真。仿真得到了满意的结果,验证了基于EPLL技术的自适应正交解调技术方案的可行性,并研究验证了算法的参数变化对其性能的影响,为今后算法在数字系统中的实现以及其在各领域的应用研究奠定了坚实的基础。
数字锁相环;自适应正交解调技术;微机电系统;柔性交流输电;数字通信;现场可编程门阵列
0 引言
广泛应用于无线电数字通信[1-2]、柔性交流输电系统(Flexible AC Transmission Systems,FACTS)[3-5]以及微机电系统(Micro-electro-mechanical Systems,MEMS)[6-8]中的数字锁相环以及解调技术,随着微电子学和计算机技术等的迅速发展,已经受到越来越广泛的关注。但是传统的数字锁相环和检测技术都存在一些缺陷,例如依据过零检测实现的全数字锁相环不仅锁相速度慢,而且过零点的扰动会直接影响锁相精度,限制了其在一些领域的应用[5];又如适合模拟电路实现的相干解调技术,在数字电路中实现则需要设计高阶数字低通滤波器,这不仅会占用大量数字电路资源并且会显著增加系统功耗[8]。
针对以上问题本文在设计一种新型全数字锁相环(All-digital Enhanced Phase-lock Loop,EPLL)的基础上,结合文献[9]中提到的自适应正交解调技术,提出了一种基于EPLL技术的自适应正交解调技术方案,并对该方案进行了研究与仿真。仿真结果验证了基于EPLL技术的自适应正交解调技术方案的可行性,得到了满意的结果,为今后的应用研究奠定了坚实的基础。
1 EPLL结构与工作原理
1.1EPLL结构
EPLL的结构与传统DPLL的结构基本相同,由鉴相器、环路滤波器和数控振荡器构成,如图1所示。与传统DPLL不同的是,EPLL的鉴相器不是简单采用一个乘法器而是由三个乘法器、一个积分器、一个90°移相器和一个加法器构成。这种鉴相器的优点是可以实时跟踪输入信号基频分量的幅值和相位,不仅可以使EPLL输出的同相分量与其输入信号保持相关,而且可以使二者保持相位同步,从而使二者的相位误差更小,并且对内部参数变化和外部噪声的影响具有更强的鲁棒性[3]。
1.2EPLL工作原理
根据EPLL的结构框图(图1),选择结构中变量A(t)、ω(t)和ϕ(t)为结构的状态变量,在合适的初始条件下可以得到系统的状态方程为:
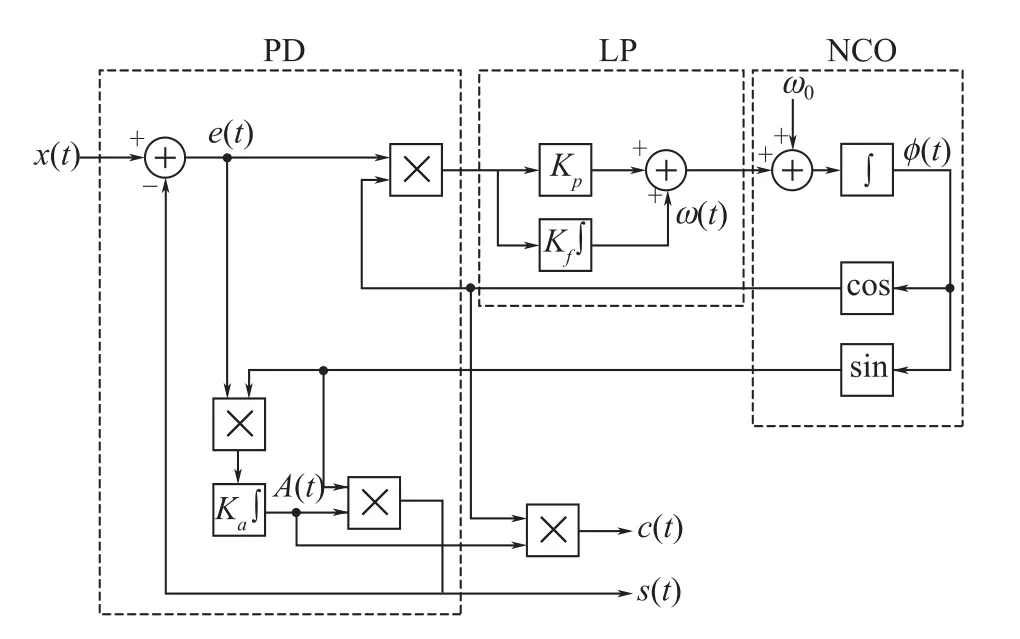
图1 EPLL结构框图Fig.1Block diagram of the EPLL
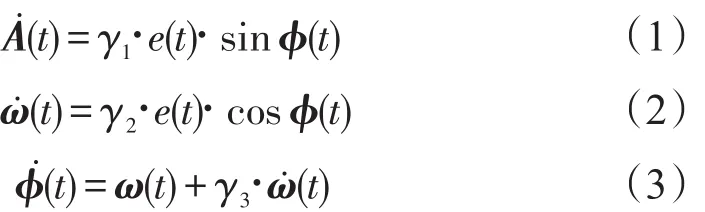
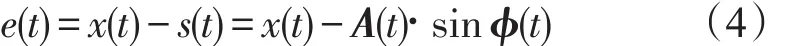
而x(t)为EPLL的输入信号,根据文献[3]可以表示为:

式中,φk(t)=ωk·t+θk为第k次谐波的相角,且ωk=kω1,n(t)为外部噪声。
1.3EPLL实现
为了在数字系统中实现上述系统,可以把上述微分方程转化为下面的微分方程形式:

其中,Ts为采样周期。EPLL的压控振荡器采用文献[10]中介绍的CORDIC算法实现,因为这样不仅可以减少实现EPLL的数字系统对存储器容量和速度的需求,而且还可以取消鉴相器中90°移相器,从而简化系统的实现。
2 自适应正交解调原理
2.1原理
自适应正交解调技术源于自适应滤波技术,就是按照一定的代价函数,对输入信号进行选择性的加权处理,使输出达到最优,并且能够跟踪和适应系统和环境的动态变化。只不过在自适应正交解调技术中,以递推方式自适应更新的不再是滤波器的系数,而是待解调信号中同相信号分量和正交信号分量的幅值。其原理框图如图2所示,其中R(k)为正交解调的参考信号,由EPLL输出信号的同相和正交分量提供,其表示为:

而x(k)为待解调的输入信号,可以表示为:

其中,n(k)为噪声信号,u(k)为待解调的真实信号,I·s(k)和Q·c(k)分别是同相信号分量和正交信号分量。自适应正交解调就是利用参考向量R(k),通过预测矩阵的迭代来获得同相信号分量和正交信号分量的幅值I和Q。

图2 自适应正交解调原理框图Fig.2Principle diagram of adaptive filtering technology
x̂(k)则为参考信号R(k)经过预测矩阵P(k)而得到的x(k)的一个估计。通过比较估计x̂(k)与输入信号x(k)得到估计误差e(k)。利用e(k)构造一个自适应算法所需要的性能函数,此性能函数根据e(k)调整预测矩阵P(k)。通过递推方式最小化性能函数,从而估计信号x̂(k)与输入信号x(k)实现匹配,得到最优的预测矩阵P(k),而预测矩阵P(k)中的分量p1(k)和p2(k)即为输入信号x(k)中同相信号分量和正交信号分量的幅值I和Q。
2.2递推算法实现


根据最速下降法可知,下一个预测向量P(k+1)等于当前预测向量P(k)加上经过比例修正的负梯度:

其中,μ为最速下降法收敛因子,其限制条件为:

λmax是矩阵N(k)的最大特征值。以误差信号每一次迭代的瞬时平方值代替其均方值来估计梯度,从而可得梯度的估计:

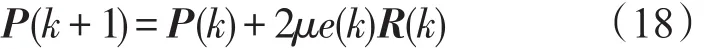
初始化P(0)=[00]T,经迭代就可得到同相信号分量和正交信号分量的幅值I和Q。
3 算法仿真
3.1EPLL算法仿真
为了验证EPLL算法的性能与参数对其性能的影响,本文在Simulink中对此算法进行了仿真。图3是EPLL在采样频率Fs=2MHz,中心频率F0=65kHz的条件下,输入信号为x(t)=sign (sin2π60000t)(即60kHz、占空比为50%、幅值为1V的方波信号)时,系统的输出波形图。其中,图3(a)是EPLL在其幅值控制系数Ka=0.03、相位的比例控制系数Kp=0.016和积分控制系数Ki=0.0008时,EPLL仿真系统的输入和输出波形图。而图3(b)和图3(c)分别是EPLL仿真系统在Ka=0.06、Kp=0.032和Ki=0.0016以及Ka=0.12、Kp=0.064和Ki=0.0032时,系统的输入和输出波形图。图3中实线描述的波形为仿真系统的输入波形,由图3也可以知道其为60kHz、占空比为50%、幅值为1V的方波信号。而点划线和点线所表示的波形是仿真系统的输出波形,其中点划线所表示的波形为系统跟踪输入信号而输出的与输入信号同步的同相信号,其与输入信号具有相同的相位,而点线表示的波形是比输入信号超前90°,但是幅值与输入信号一致的正交信号。

图3 EPLL在不同参数下的仿真波形Fig.3Simulation wave-forms of the EPLL with different parameters
由图3(a)可知,当Ka=0.03、Kp=0.016、Ki=0.0008时,EPLL系统需要15个方波周期才可以稳定收敛,而由图3(b)可知,当Ka=0.06、Kp=0.032、Ki=0.0016时,系统只需要10个方波周期就可以稳定收敛,并且由图3(c)可知,当Ka=0.12、Kp=0.064、Ki=0.0032时,系统稳定收敛需要的方波周期数最少,仅仅需要5个就已经稳定收敛了,但是随着收敛速度的加快,系统跟踪精度降低,由图3(a)~图3(c)可以看出系统输出信号波形的失真越来越大。从上面的分析可以得出一个简单的结论:Ka主要影响EPLL系统对输入信号幅值的跟踪特性,Kp和Ki则主要影响系统对输入信号相位的跟踪特性,当增大Ka、Kp和Ki时,系统对输入信号的跟踪速度就会加快,但是跟踪精度就会随之降低,反之即然。
从图3还可以得知,本文设计的EPLL就是一个自适应陷波滤波器,因为从EPLL的输入和输出可以明显地知道EPLL可以精确地跟踪输入信号的基波成分而抑制信号的任意次谐波成分,图4描述的即是EPLL在图3(a)的参数条件下所抑制滤除输入方波信号中的总谐波成分。为了更明显地表现EPLL对输入信号谐波的抑制功能,本文分别对其输入信号和输出信号进行了频谱分析,分析结果如图5所示,其中图5(a)为输入方波信号的频谱图,图5(b)为输出信号的频谱图。从图5(b)可以清晰地看到EPLL的输出信号中只有输入信号中的基波成分,而其他任意次谐波成分已经完全被EPLL滤除。
3.2EPLL自适应正交解调算法仿真
同样本文为了验证EPLL自适应正交解调算法的正确性与参数μ对其性能的影响,在Simulink中对此算法也进行了仿真试验,图6是算法在输入信号x(t)=sin(2π3000t)+n(t)时,EPLL系统输出的波形图。其中,n(t)用于表示均值为0,方差=1的高斯噪声。信号的采样频率Fs=2MHz与EPLL仿真时相同。图6(a)和图6(c)是算法解调输入信号为x(k)时,输出的信号正交分量的幅值波形图,而图6(b)和图6(d)则是解调x(k)时得到的同相分量的幅值波形图,从仿真结果可以看出,在EPLL解调算法输出的信号中噪声得到了明显减少,信噪比得到了明显提高。因此,此算法具有很强的噪声抑制能力。

图4 输入方波信号的总谐波成分Fig.4Total harmonic components of the input square wave signal

图5EPLL输入输出信号的频谱图Fig.5Spectrum of the input&output signal of the EPLL
图6不仅验证了算法的可行性,同时还描述了不同收敛因子μ对算法性能的影响,图6(a)和图6 (b)为算法在μ=0.03时的仿真波形,而图6(c)和图6 (d)则为其在μ=0.003时的仿真波形。从波形图可以容易看出增大μ值可以增快算法的收敛速度,但是解调算法输出信号的误差相应增大;而如果减小μ值虽然可以增加算法的解调精度,但是收敛速度就会变慢。因此,在实际选择收敛因子μ时要折中考虑收敛速度和解调精度两个方面。如果实际应用对收敛速度和解调精度两方面要求都比较苛刻,为了满足实际需求可以对算法进行简单的修改,如在解调开始时采用大的步长以加快收敛速度,等稳定后将步长变小以提高解调精度。
4 结论
本文设计的基于EPLL技术的自适应正交解调方案,通过了仿真验证,得到了满意的结果,并研究验证了算法的参数变化对其性能的影响,为今后算法在数字系统如FPGA中的实现以及其在各领域的应用研究奠定了坚实的基础。
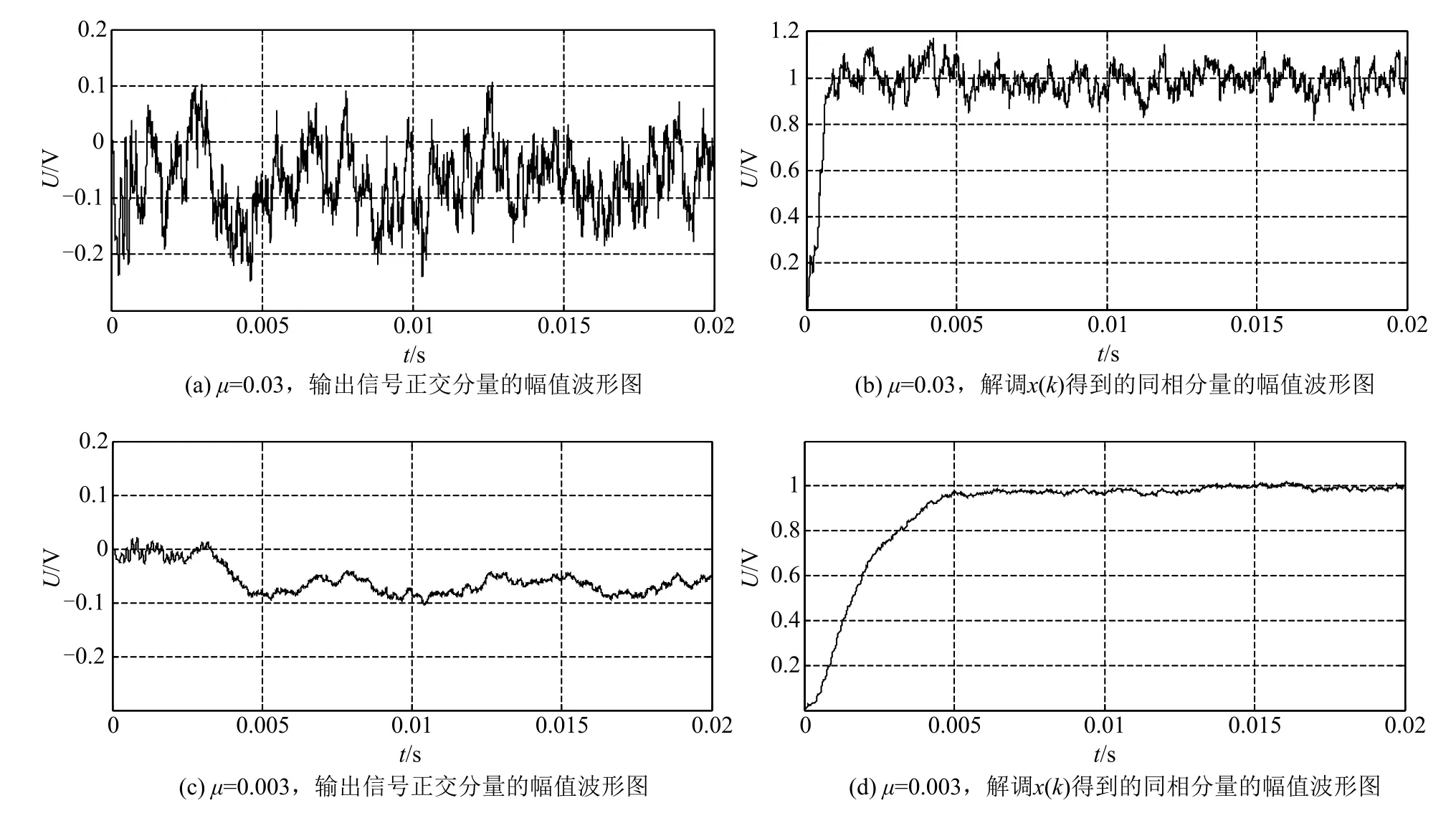
图6 EPLL自适应正交解调算法在不同参数下的仿真波形Fig.6Simulation wave-forms of the AQDT based on EPLL at different parameters
[1]T.Grydeland,F.D.Lind,P.J.Erickson,J.M.Holt.Software radar signal processing[J].Annales Geophysicae,2005,23(1):109-121.
[2]N.Sonowal,R.Yadav,S.kannan.Real time GPS software receiver with new fast signal tracking method[C]. 2008 IEEE International on Conference Radio and Wireless Symposium(RWS),2008:231-234.
[3]M.Karimi-Ghartemani,M.R.Iravani.A method for synchronization of power electronic converters in polluted and variable-frequency environments[J].IEEE Transactions on Power Systems,2004,19(3):1263-1270.
[4]M.Karimi-Ghartemani,O.Boon-Teck,A.Bakhshai.Application of enhanced phase-locked loop system to the computation of synchrophasors[J].IEEE Transactions on Power Delivery,2011,26(1):22-32.
[5]M.Ghartemani,M.Mojiri,A.Safaee,J.Walseth,et al.A new phase-locked loop system for three-phase applications[J].IEEE Transactions on Power Electronics,2013,28(3):1208-1218.
[6]R.Neul,U.Gómez,K.Kehr,et al.Micromachined gyros for automotive applications[C].The 4thIEEE Conference on Sensors,2005:527-530.
[7]Eik-Arnold,Franz-Nuscheler.Compensation methods for a silicon tuning fork gyroscope[J].Microsystem Technologies,2008,14(4/5):623-628.
[8]Yuliang Wang,Shuangwei Han,Hongsheng Li,Hao Liu. Research and test of the digital phase locked loop drive technology for silicon micro-machined gyroscope[C].7thInternational Conference on MEMS,NANO and Smart Systems of Advanced Materials Research,November,2011:4252-4259.
[9]Yuliang Wang.Research and test of the adaptive quadrature demodulation technology for silicon micro-machined gyroscope[J].Journal of Harbin Institute of Technology,2012,19(5):118-122.
[10]王玉良.基于CORDIC算法的PLL在FPGA中的实现[J].计量学报,2012,33(3):259-265. WANG Yu-liang.FPGA implementation of PLL based on CORDIC algorithm[J].Acta Metrologica Sinica,2012,33(3):259-265.
Research on a NewAdaptive Quadrature Demodulation Technology Based on EPLL
WANG Yu-liang,XING Chao-yang,ZHENG Xu-dong,ZENG Qing-lin
(Beijing Institute ofAerospace Control Devices,Beijing 100039)
The all-digital phase-locked loop(ADPLL)achieved by using zero-crossing detection technology not only has slow lock-in speed but also its lock-in precision will be directly affected by the zero-crossing disturbance.Furthermore,coherent detection technique generally used for amplitude detection is suitable for realization using analog circuits. It will take up a large number of digital resources and significantly increase the power consumption of the system that a high-order digital low-pass filter needs to be designed for the implementation of coherent detection by digital circuits.In order to solve these problems,a new all-digital enhanced phase-lock loop(EPLL)is devised and based on that a new adaptive quadrature demodulation technology(AQDT)program combing EPLL and AQDT is proposed,researched and simulated.The satisfactory simulation results prove the feasibility of the program and verify the parameter changes on the performance of this algorithm that lays the foundation for the further implementation of it in a digital system and its application research in all fields.
digital phase-locked loop;adaptive quadrature demodulation technology;micro-electro-mechanical systems;flexibleAC transmission systems;digital communications;field programmable gate array
TN98
A
1674-5558(2016)02-01034
10.3969/j.issn.1674-5558.2016.01.010
王玉良,男,博士,研究方向为MEMS陀螺及医用超声信号处理。
2014-12-09

