超声波散射有限元模型中单一模态入射研究

刘会彬，郑阳，郑晖，邬冠华



超声波散射有限元模型中单一模态入射研究

刘会彬1,2，郑阳2，郑晖2，邬冠华1

(1. 南昌航空大学无损检测技术教育部重点实验室，江西南昌330063；2. 中国特种设备检测研究院，北京100029)

超声波在缺陷处的散射行为分析中，研究单一模态与缺陷的作用极为重要。通过在多个节点上沿特定方向上施加简谐力形成合成点源，分析和验证了单一纵波和横波有限元模型的稳定性及近似为平面波的监测距离。仿真结果表明：单一纵波位移场纵波相对幅值变化率在±1.5%范围内波动，相位变动幅度为±0.6°，近似单一横波位移场横波相对幅值变化率在±0.5%范围内波动，相位变动幅度为±20°；当监测距离大于10时，超声横波可近似认为是平面波；当监测距离大于5时，纵波可近似为平面波。单一纵波有限元模型显示出较好的稳定性。此模型的建立为单独分析单一模态对缺陷的散射特性、模态转换及高精度定量检测提供了支撑和依据。

超声波；散射; 有限元；合成点源；单一模态激励；

0 引言

弹性波与散射体的相互作用是一个重要的问题，它发生在很多不同的领域，如无损评价、地震学及医学成像等。弹性动力学散射过程的数学建模是极具挑战性的课题。长期以来，大量的文献围绕着此项研究展开，目前，只有在一些很简单的散射体如球形、柱形处的超声波散射获得了数学模型和精确的解析解。对于一些形状稍复杂的缺陷，在一定的条件下，可以用近似解表达其散射情况，如当散射体尺寸和形状变化都较超声波波长大时，可以采用Kirchhoff近似求解。当夹渣类缺陷的物理性能与母材差别不是很大时，可以采用Born近似的方法进行求解。但对于实际中众多复杂缺陷的散射特性，往往难以进行解析求解，只能借助于数值方法进行研究，代表性的计算方法有有限元法、有限差分法、边界元法。

近年来，随着计算机技术的飞速发展，使其计算能力能够快速地应用于散射问题的数值求解。采用有限元或有限差分将连续问题转化为离散问题，并运用计算机直接进行数值模拟，在建立模型、参数选取及对模拟结果的数据处理方面，与实物模拟试验相比更具有灵活性与优越性[1]。M V Felice等[2]对应力腐蚀裂纹的超声波散射分别采用基尔霍夫近似与频域有限元方法模拟，在缺陷间的反射、裂纹尖端衍射、短裂纹散射方面，频域有限元技术更能实际反应超声波与缺陷的交互作用。Frehner等[3]对地震学中弹性动力学体波散射问题分别采用有限元及有限差分法模拟，在计算效率方面有限元法优于有限差分法。

前人所做的工作为超声波散射的仿真奠定了坚实的基础，特别是弹性动力学散射中有限元方法的引入。基于商业有限元软件包在弹性动力学建模的广泛应用，散射问题的求解也逐渐得到解决。

在实际生活中，存在不均匀区的可能性是很大的。于是常需要了解它是否存在，以及它是什么性质的。对不透明固体，需要用非光学的检测手段。内部的不均匀区常称缺陷或伤，文章中有时称之为散射区或称散射体[4]。Paul D. Wilcox等[5]提出的有限元技术仅局限于各向同性材料二维散射并且不能够立即应用于其他几何体或者各向异性材料，此外，模态分离带来了不必要的不稳定性。Jie Zhang等[6]建立了基于合成点源的超声纵波有限元模型并利用超声阵列技术测量了裂纹类缺陷的长度及方位角，实验与仿真结果进行了对比。Alexander Velichko等[7]提出了有限元局部散射模型用于预测各向异性材料中任意形状的缺陷处的远场散射行为，优化了paul D. Wilcox 提出的有限元模型，并在此基础上应用积分的思想，简化了求解散射矩阵繁杂的重复建模过程。国内方面，李树榜等[8]通过有限元分析模拟与光弹实验对比，研究了圆柱形孔脉冲超声波的散射问题，并通过有限元模拟了裂纹的超声散射行为[9]，但对散射行为并未从理论上做进一步的解释。田红[10]分别对浸没于盛满水的圆柱形容器中的刚性球、液体球及气泡球对超声波的散射进行了仿真实验研究，表明不同性质的球体其超声波幅射面附近的声强分布及声强大小不同。朱为勇等[11]研究了柱状固体复合材料对斜入射超声波的散射，阐述了三层柱状固体复合材料入射超声波的散射理论，建立了描述界面薄层的三维弹簧物理模型，分析了固体界面处的声学边界条件，从数值上研究了玻璃纤维/铝基复合结构中界面薄层力学参量的变化对斜入射超声散射截面积的影响。刘胜兴等[12]研究了横向各向同性柱状复合结构对超声波的散射。将柱状复合结构中各向异性界面薄层相应的转移矩阵作渐近展开，建立了模拟这种界面薄层的弹簧模型及界面处广义边界条件。在超声散射应用方面，明廷锋等[13]在被测悬浮液不透明时光散射测粒技术应用受限而提出了一种超声波散射式颗粒测量方法，并讨论了如何避免测量结果的多值性。张翔等[14]分析了复合材料空隙形貌特征对超声波散射衰减的影响。王耀俊等[15]介绍了圆柱状固体中超声波散射频谱方法的原理和实验方法，讨论声散射谱技术在材料无损评价中的应用前景。中国科学院的沈建中等[16]从理论方面研究了固体内部具有自由表面的无限长带状裂缝对平面纵波或平面SV横波超声脉冲的散射，采用拉氏变换和广义Wiener-Hopf方法，给出了散射声场在拉氏域的表达式。但以上研究工作都是基于相对简单的散射体，对形状稍复杂的散射体，仍没有建立合适的数学模型。

本文中采用合成点源的方式进行加载，利用有限元仿真软件ABAQUS建立了单一模态二维超声散射有限元模型，并从监测信号位移分布、相对幅值变化率、相位的变化验证了此模型的正确性及稳定性。此模型的建立为单独分析单一模态对缺陷的散射特性、模态转换以及高精度定量检测提供了依据。

1 有限元建模

超声波在固体中的散射问题，是超声学科中的一个基本问题。超声波一经产生，即向前传播。超声波碰上了媒质的边界或在媒质内部的局部不均匀区，原来单向传播的超声波被干扰向各方散开的现象，成为散射现象。了解超声遇到非均匀区的散射性能，从而根据不同类型非均匀的散射特征，反过来确定这个区的状态, 例如区的形状、大小等，成为检测应用的基础。传统声学所讨论的媒质是流体,包括气体和液体。对流态媒质，已进行了多年的散射分析，取得了一些有益的结果。在开辟超声应用后，媒质对象扩大到固体，固体中的散射问题成为新的课题，从50年代才开始得到认真的考虑。到70年代后期，随着定量检测需要的增长，散射课题得到新的、更广泛的重视，至今未衰。固体内超声的传播现象，比起流体要复杂些，主要原因是，不计固体可能有的各向异性，在固体内可以存在横波，而且纵波和横波之间有模式转换，即纵波和横波的耦合[4]。超声波与缺陷的相互作用是一个复杂的问题，超声波在缺陷处的模式转换使得超声波散射的研究变得非常复杂。研究单一模态的超声波，可以简化超声波散射的过程，对超声波与缺陷的相互作用研究极为重要。

建模流程可以概括如下：有限元模型采用圆形计算区域，以合成点源几何中心为圆心，六个同心圆作为360°方向的散射信号监测圆，其上间隔11.25°设置一个信号接收点，在计算区域四周采用吸收边界消除边界的反射回波。通过在多个节点上沿特定方向上施加简谐力形成合成点源，产生单一纵波及横波。

1.1 合成点源

采用有限元软件ABAQUS进行建模，并采用支持面内位移的所有弹性动力学波模态的ABAQUS/Explicit 进行求解。一般说来，对相控阵而言，缺陷处于超声阵列的远场区，缺陷处的超声波可以近似为平面波，因此在有限元模型中对于给定缺陷怎样从任意方向产生平面波是一个难点。合成点源技术在缺陷足够远处产生的对称声波可以近似为平面波，其有效距离依赖于缺陷尺寸。当超声入射波的曲率与缺陷尺寸相比可以忽略不计时，波阵面可近似为平面波。

1.2 单一纵波

图1所示为8节点合成点源不含缺陷及含椭圆缺陷的有限元模型及快照图。计算中选取Q 235钢板作为被检材料，激励信号采用频率为5 MHz(周期为=0.2)的五个周期的汉宁窗调制的正弦波，在8个节点上沿半径方向同时加载时域激励信号，近似产生了朝各个方向辐射的对称纵波。用于验证性的有限元模型采用圆形计算区域主要有两方面的依据。其一，采用圆形计算区域更符合点源辐射声波的传播规律；其二，采用圆形计算区域可以减少计算时间。模型尺寸为直径(为波长)。模拟时假设模型是二维的，意味着模型在第三个维度下尺寸是无限大的。准二维缺陷在实际情形下是很常见的，例如焊接板材中沿焊接线方向的缺陷；此外，与三维相比，简化了计算和实验过程，原则上，采用同样的方法可以将二维缺陷的模拟拓展到三维缺陷的模拟。平面应变单元假设里面应变ε33为零，可以用来模拟厚结构。合成点源位于圆心，在合成点源的方形区域内，为了缩短分析时间及使方形区域内合成点源激励信号施加到指定节点上，采用四边形应变减缩积分单元CPE4R划分网格，在其他区域采用三角形应变单元CPE3划分网格[5-6](CPE4R是由四个节点组成的平面应变实体减缩积分单元，CPE3是由3个节点组成的平面应变实体单元)。为了得到合成点源在不同传播距离的位移值，通过监测点的位移可以探测到声波的波动，用于验证产生的超声波是否对称。以合成点源几何中心为圆心，直径分别为、、、、及的六个同心圆作为360°方向的散射信号监测圆，其上间隔11.25°设置一个信号接收点，角度定义如图1(a)所示。图1(b)为不含缺陷的快照图，其在圆周方向纵波能量分布均匀；图1(c)为单一纵波含椭圆缺陷的仿真模型，模型的参数与单一纵波不含缺陷的仿真模型一致，创建的椭圆缺陷(长轴、短轴分别为、)位于模型正中心，合成点源的中心尽可能靠近轴正半轴，半径为的节点。图1(d)为单一纵波含椭圆缺陷的快照图，可以明显看到超声纵波遇到椭圆缺陷时，原来单向传播的超声纵波被干扰，经模态转换成其他形式的声波。模态转换形成的声波包含的缺陷信息，对超声成像至关重要。在研究超声波在缺陷处的散射时，一方面为了满足圆环波前纵波近似为平面波前纵波的条件，必须使激励点与散射体有一定的距离；另一方面，为了有效地分离出散射信号，还需要避免边界回波的影响，即激励信号和接收点均要离边界有足够的距离，从而使得模型面积很大，节点数将会很多，使得计算时间过长，甚至超出计算机内存许可而不可计算。采用吸收边界可以有效解决以上问题。本模型中的吸收边界采用以下方法设置：吸收边界中材料所有属性参数在保持与计算区域中材料属性一致的基础上，加入阻尼项，这使得计算区域与吸收边界临界处的声阻抗变化很小，同时弹性波在吸收边界逐层衰减，达到实际边界时，弹性波衰减得相当小。材料阻尼在中心区域为0，到达最外层时，阻尼达到最大值，按照瑞利阻尼定义，其瑞利阻尼系数的变化规律为[17-18]：

(a)                     (b)

(1) 网格最大尺寸需满足：

表1 单一纵波有限元仿真模型参数列表

(2) 最大时间步距需满足：

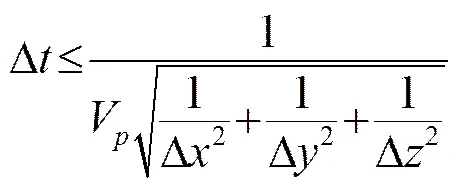
1.3 单一横波

为了得到产生单一横波的最佳激励方式,分别采用单节点、8节点合成点源、16节点合成点源及32节点合成点源作为激励信号加载点，其单节点、8节点合成点源、16节点合成点源及32节点合成点源如图2所示。计算中选取Q 235钢板作为被检材料，激励信号采用频率为5 MHz(周期为=0.2)的五个周期的汉宁窗调制的正弦波，分别在各节点上沿切向按图2箭头所示方向(切线方向)同时加载时域激励信号。用于验证性的有限元模型采用圆形计算区域，其尺寸为直径。合成点源位于圆心，图2(a)、图2(c)及图2(d)中均采用三角形应变单元CPE3划分网格，图2(b)中在合成点源的方形区域内采用四边形应变单元CPE4R划分网格，在其他区域采用三角形应变单元CPE3划分网格。为了得到合成点源在不同传播距离的位移值，通过监测点的位移可以探测到声波的波动，用于验证产生的超声波是对称的。以合成点源几何中心为圆心，直径分别为、、、、及的六个同心圆作为360°方向的散射信号监测圆，其上间隔11.25°设置一个信号接收点，角度定义如图2所示。在计算区域四周采用吸收边界消除边界的反射回波。其吸收边界的设置与单一纵波时一致。网格单元和求解时间步距在满足式(1)和式(2)的前提下，网格尺寸设置为，其中表示超声波横波波长，求解时间步距设置为1.0×10-9s。横波有限元仿真模型参数设置见表2。

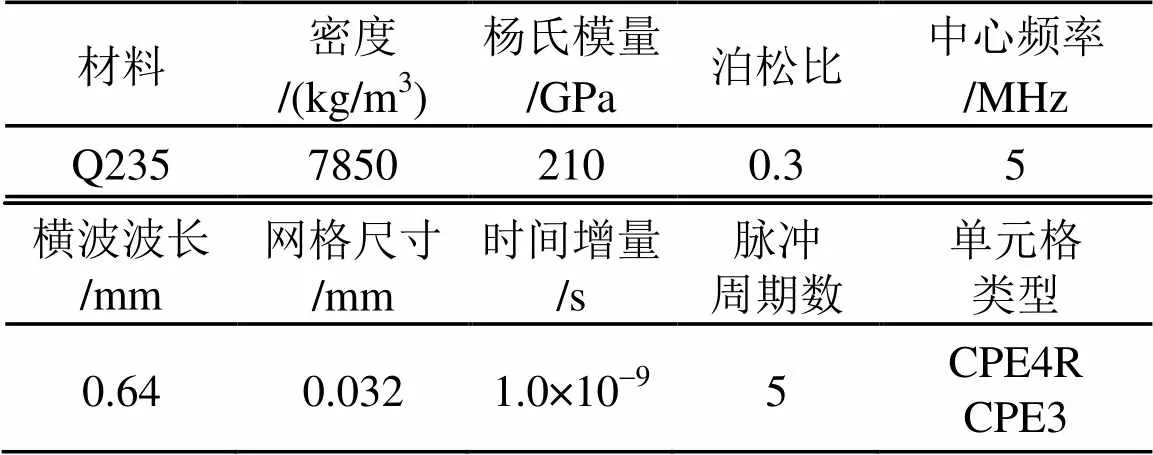
表2 横波有限元仿真模型参数表

2 仿真结果与分析

2.1 单一纵波

为了验证8节点合成点源产生的单一纵波的对称性，对合成点源周围的监测点的位移大小一致性进行了测量。理论上，当时，位移大小随着的增加而递减。因此，如果乘以，所有监测圆上节点的位移大小应相等。图3为归一化幅值与监测角度的变化曲线，纵坐标为归一化幅值，四个监测圆上的监测点处的位移大小分别乘以，再除以平均值求得归一化位移幅值。从图3可以看出，归一化幅值在监测距离大于(为超声波纵波波长)时有低于3%的误差，且随着监测距离的增加，归一化幅值误差越来越小。由此得出，经过距离后，超声纵波在任意方向都是严格对称的，波前可以近似为平面波。为了进一步分析单一纵波有限元模型的稳定性，对监测半径为的监测节点处位移最大值的变化率及位移最大值处对应相位的变化进行了分析。如图4(a)所示，纵坐标为相对幅值变化率，相对幅值变化率由位移最大值与平均值的差值除以平均值求得，图中实心圆点为各个监测角度的相对幅值变化率。纵波相对幅值变化率在±1.5%范围内波动，相位变动幅度为±0.6°。因此，单一纵波有限元模型显示了较高的稳定性。

(a) 相对幅值变化率

(b) 相位变化率

图4 单一纵波 (a) 相对幅值变化率曲线；(b) 相位变化曲线

Fig.4 A single longitude wave: (a) relative amplitude variation; (b) phase variation

2.2 单一横波

图5所示为单节点、8节点合成点源、16节点合成点源及32节点合成点源的横波快照图。横波值越大，其灰度越高。主应力值分布直接影响云图快照图是根据色彩带主应力值显示灰度的，主应力中声波能量的分布，主应力值越大的区域其声波振动能量越大。单节点、16节点、32节点激励产生的横波都有不同程度的缺口，横波能量分布不均匀。图5(a)、5(c)、5(d)中横波在轴方向其灰度值几乎与周围区域一致，如果在此方向上存在缺陷，就很容易造成漏检。图5(b)中，横波在圆周方向灰度分布均匀，8节点合成点源产生的横波能量分布均匀，且激励的超声纵波成分与超声横波相比很微弱。因此，8节点合成点源激励的超声横波为最佳，在不考虑超声纵波的影响时，8节点激励产生的横波可近似认为是单一横波。

(a) 单节点

(b) 8节点

(c) 16节点

(d) 32节点

图5 横波快照图(a) 单节点；(b) 8节点；(c) 16节点；(d) 32节点

Fig.5 Transverse wave snapshots: (a) a single node; (b) 8 nodes; (c) 16 nodes; (d) 32 nodes

(a)

(b)

图6 (a) 距点源5处的纵波及横波位移曲线；(b) 横波与纵波位移差曲线

Fig.6 (a) The longitudinal wave and transverse wave displacement curves at 5from the point source; (b) Displacement difference curve between transverse wave and longitude wave

图6为距点源5处的纵波及横波位移及位移差曲线。从图6(a)可以看出，由8节点合成点源产生的超声横波圆周范围内不同角度上辐射的声波能量还是有差别的，在某些监测角度方向横波位移大小比其他角度大，在各个监测角度方向横波分布也不均匀，但是在某些角度上，如图6(b)所示其横波位移比纵波位移大，在这些角度监测范围(60°~120°及240°~300°)内可以近似为单一横波。单从距点源5处的纵波及横波位移曲线很难分析得出波前可以近似为平面波的距离。为了尽可能得到平面波近似距离，本文将由分析整个圆周内超声横波能量的均匀性转化为分析离合成点源几何中心同一距离圆周上某个点处2个波长范围内的超声横波能量的均匀性，即在2个波长长度范围内只要超声横波位移大小在一定的范围内变化，此时的距离即可近似认为是平面波近似距离。如图7所示，横坐标为信号监测点到激励点源的距离，纵坐标为最大位移幅值变化率，其中，2个波长范围内设置了5个监测点，在每个监测点处求得位移最大值和5个监测点位移最大值的平均值，最大位移幅值变化率由监测点处的位移的最大值除以平均值计算得到。图中的实心圆点表示同一监测距离处位移幅值变化率的最大值。由图7可知，监测距离在时最大位移幅值变化率在6.8%左右，当监测距离大于时，最大位移幅值变化率在3%以内，位移分布呈现了很好的一致性，所以当监测距离大于时，得到的超声横波可近似认为是平面波。因此当缺陷位于传感器10倍波长的距离时，通过监测缺陷处的散射场，计算得到缺陷处的散射矩阵，进一步分析单一横波在缺陷处的散射特性及模态转换过程并有望实现缺陷的重建。

为了进一步分析横波有限元模型的稳定性，对监测半径为5的监测节点处位移最大值的变化率及位移最大值处对应相位的变化进行了分析。如图8(a)所示，纵坐标为相对幅值变化率，相对幅值变化率由位移最大值与平均值的差值除以平均值求得，图中实心圆点为各个监测角度的相对幅值变化率。横波相对幅值变化率在±0.5%范围内波动，相位变动幅度为±20°。

(a)

(b)

图8 横波(a)相对幅值变化率曲线；(b) 相位变化曲线

Fig.8 Transverse wave: (a) relative amplitude variation; (b) phase variation

3 结论

本文建立了单一模态二维超声散射有限元模型，采用了合成点源作为信号激励的方法，得到以下主要结论：

(1) 通过8个节点简谐力的作用形成了合成点源，近似的单一横波和单一纵波均可以通过上述合成点源得到。

(2) 无论是单一纵波还是横波，其监测圆上的位移幅值都是近似相等的。当监测距离大于时，单一纵波位移幅值出现2%的相对误差，超声纵波在任意方向都是严格对称的，波前可以近似为平面波。监测距离在时，超声横波最大位移幅值变化率在6.8%左右；当监测距离大于时，超声横波最大位移幅值变化率在3%以内，可以近似认为是平面波。

(3) 单一纵波相对幅值变化率在±1.5%范围内波动，相位变动幅度为±0.6°；横波相对幅值变化率在±0.5%范围内波动，相位变动幅度为±20°。

上述模型总体上均表现出较好的稳定性，此模型的建立为单独分析单一模态对缺陷的散射特性、散射矩阵的提取、在缺陷相互作用过程中的模态转换、缺陷重建甚至高精度的定量检测提供了支撑和依据。

[1] 廖振鹏. 近场波动的数值模拟[J]. 力学进展, 1997, 27(2): 193-212.

LIAO Zhenpeng. Numerical simulation of near-field wave Motion [J]. Advances in Mechanics, 1997, 27(2): 193-212.

[2] Felice A. V. M V, Wilcox P D, Barden T, et al. Obtaining geometries of real cracks and using an efficient finite element method to simulate their ultrasonic array response[J]. UT SIMULATION, 2014, 56(9): 492-498.

[3] Marcel Frehner S. M. S. Comparision of finite difference and finite element methods for simulating two-dimensional scattering of elastic waves[J]. Physics of the Earth and Planetary Interiors, 2008, 171(1-4): 112-121.

[4] 应崇福. 超声波在固体中传播和散射的研究[J]. 中国科学院院刊, 1990(1): 56-59.

YING Congfu. The research of ultrasonic wave scattering and tranmiting in solid[J]. The Proceedings of the Chinese Academy of Sciences, 1990(1): 56-59.

[5] Wilcox P D, Velichko A. Efficient frequency-domain finite element modeling of two-dimensional elastodynamic scattering[J]. J Acoust Soc Am, 2010, 127(1): 155-165.

[6] ZHANG Jie, Bruce W Drinkwater, Paul D Wilcox. Defect characterization using an ultrasonic array to measure the scattering coefficient matrix[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55(10): 2254-2265.

[7] Velichko A, Wilcox P D. A generalized approach for efficient finite element modeling of elastodynamic scattering in two and three dimensions[J]. J Acoust Soc Am, 2010, 128(3): 1004-1014.

[8] 李树榜, 李书光, 刘学锋. 固体中圆柱形孔脉冲超声波散射的有限元模拟[J]. 声学技术, 2007, 26(3): 417-421.

LI Shubang, LI Shuguang, LIU Xuefeng. Finite element modeling of pulsed ultrasonic waves scattered from cylindrical hole in solid [J]. Technical Acoustic, 2007, 26(3): 417-421.

[9] 李树榜, 李书光, 刘学锋. 裂纹超声散射的有限元模拟[J].无损检测, 2007, 29(1): 27-32.

LI Shubang, LI Shuguang, LIU Xuefeng. Finite element modeling of ultrasonic waves scattering on cracks [J]. Nondestructive Testing, 2007, 29(1): 27-32.

[10] 田红. 不同性质的球体对超声波散射的有限元分析[J]. 广东石油化工学院学报, 2015, 25(1): 50-55.

TIAN Hong. Finite element analysis of ultrasonic scattering by different propertities spheres[J]. Journal of Guangdong University of Petrochemical Technology, 2015, 25(1): 50-55.

[11] 朱为勇, 王耀俊. 柱状固体复合结构对斜入射超声波的散射[J]. 声学学报, 1997, 23(4): 305-314.

ZHU Weiyong, WANG Yaojun. Scattering of obliquely incident ultrasonic waves by a cylindrically layered solid structure.[J]. ACTA ACUSTICA, 1997, 23(4): 305-314.

[12] 刘胜兴, 王耀俊. 横向各向同性柱状复合结构对超声波的散射[J]. 声学学报, 2002, 27(2): 149-156.

LIU Shengxing, WANG Yaojun. Sound scattering by cylindrical layered structures with transversely isotropic symmetry [J]. ACTA ACUSTICA, 2002, 27(2): 149-156.

[13] 明廷锋, 朴甲哲, 张永祥. 超声波散射式颗粒测量及其测量结果单值性的分析[J]. 计量学报, 2006, 27(2): 179-182.

MING Tingfeng. PIAO Jiazhe, ZHANG Yongxiang, Particle Detection Based on Ultrasonic Scattering and Monodromic Discussion of Its Measurement"[J], ACTA METROLOGICA SINICA, 2006, 27(2): 179-182.

[14] 张翔, 陈军, 林莉, 等. 复合材料孔隙形貌特征对超声波散射衰减影响的分析[J]. 中国机械工程, 2010, 21(14): 1735-1741.

ZAHNG Xiang, CHEN Jun, LIN Li, et al. Effect on ultrasonic scattering attenuation coefficient of morphological characteristics of voids in composite materials[J]. Journal of Chinese Mechanical Engineering, 2010, 21(14): 1735-1741.

[15] 王耀俊, 刘胜兴, 王铁海. 柱状材料对超声波的散射及应用[J]. 声学技术, 2002, 21(增刊): 227-228.

WANG Yaojun, LIU Shengxing, WANG Tiehai. Ultraonic scattering by clindrical materials and its applications[J]. Technical Acoustics, 2002, 21(suppl.): 227-228.

[16] 沈建中, 应崇福, 李明轩. 固体中带状裂缝对脉冲超声波散射的理论分析[J]. 声学学报, 1985, 10(1): 13-22.

SHEN Jianzhong, YING Chongfu, LI Mingxuan. Scattering of an ultrasonic pulse by a two-dimensional crack in solid-general theoretical analysis. [J]. Acta Acustica, 1985, 10(1): 13-22.

[17] Prabhu Rajagopal, Mickael Drozdz M, Elizabeth A Skelton. On the use of absorbing layers to simulate the propagation of elastic waves in unbounded isotropic media using commercially available Finite Element packages[J]. NDT & EInternational, 2012, 51(3): 30-40.

[18] 吴斌, 张也弛, 郑阳,等. 超声导波有限元仿真中吸收边界设置及参数[J]. 北京工业大学学报, 2013, 39(12): 1777-1783.

WU Bin, ZHANG Yechi, ZHENG Yang, et al. Modeling and parameters of absorbing boundary for ultrasonic-guided wave in FE simulation[J]. Beijing University of Technology, 2013, 39(12): 1777-1783.

Single mode incident for finite element model of ultrasonic scattering

LIU Hui-bin1,2, ZHENG Yang2, ZHENG Hui2, WU Guan-hua1

(1. Key Laboratory of Nondestructive Testing of Ministry of Education， Nanchang Hangkong University, Nanchang 330063,Jiangxi,China; 2.China Special Experiment Inspection and Research Institute,Beijing 100029,China)

It is very important to study the interaction of single mode defect in the analysis of scattering behavior of ultrasonic wave. By applying the harmonic forces in a particular direction to building resultant sources at multiple nodes, the singlelongitudinal wave mode and approximately single shear wave mode can be obtained, and the monitoring distance, where the longitudinal or shear wave could be approximately considered as a plane wave, and the stability of the corresponding finite element models havebeen analyzed. Simulation results show that the displacement fields exhibit the relative amplitude fluctuations of ±1.5% and phase fluctuations ± 0.6° for the single longitudinal wave, and exhibit the relative amplitude fluctuations of ± 0.5% and phase fluctuations within ± 20° for the approximately single shear wave; when the monitoring distance is greater than10the obtained shear wave could be approximately considered as a plane wave and the model shows good stability in performance; and when the monitoring distance is greater than 5λ the obtained longitudinal wave could be approximately considered as a plane wave. The established finite element models provide a basis and support for the separate analysis of a single mode on defect scattering characteristics, modal conversion and high accuracy quantitative detection.

ultrasonic wave; scatter; finite element; resultant sources; single mode excitation;

TG115.28

A

1000-3630(2016)-01-0129-08

10.16300/j.cnki.1000-3630.2016.02.009

2015-07-08;

2015-08-25

质检总局科技计划项目(2014QK252); 质检公益性行业科研专项项目(201410026)

刘会彬(1990－), 男, 江西赣州人, 硕士研究生, 研究方向为电磁超声检测技术。

郑阳, E-mail: zhengyangchina@126.com