基于最小二乘支持向量机的硅压阻式传感器温度补偿*
杨遂军,康国炼,叶树亮
(中国计量大学工业与商贸计量技术研究所,杭州310018)
基于最小二乘支持向量机的硅压阻式传感器温度补偿*
杨遂军,康国炼,叶树亮*
(中国计量大学工业与商贸计量技术研究所,杭州310018)
针对硅压阻式传感器灵敏度和零点温度漂移大、硬件补偿电路效果不佳的问题,提出最小二乘支持向量机方法对其温度漂移进行补偿。首先分析了经硬件补偿后的硅压阻式传感器的温度漂移特性,在整个检测范围内选取均匀分布的温度、压力数据作为模型输入,经预处理后对输出数值进行训练,并运用网格搜索法和交叉确认法优化模型的惩罚因子和正则化参数,建立了传感器温度补偿模型。实验结果表明,基于最小二乘支持向量机的温度补偿算法在0~100℃温度范围内把传感器输出综合精度从3.2%FS提高到0.25%FS,进一步提高了传感器的精度和温度使用范围,具有较高的实用价值。
硅压阻式传感器;温度漂移;温度补偿;最小二乘支持向量机
EEACC:7230doi:10.3969/j.issn.1004-1699.2016.04.007
硅压阻式传感器是利用半导体材料硅的压阻效应制备的压力传感器,具有动态响应快、灵敏度高以及易于小型化等优点,已广泛应用于工业领域[1]。但半导体材料硅因其固有特性对温度存在交叉敏感,导致硅压阻式传感器的灵敏度和零点受温度影响产生漂移[2-3]。在宽温、高精度的压力检测场合,例如化学品热危险性评估和理化参数测试中,必须对其温度漂移进行补偿。
商品化的硅压阻式传感器在出厂时已通过硬件电路对其温度漂移进行补偿,但由于硬件特性限制仍存在补偿温度范围小、精度低等问题,不能满足宽温、高精度的压力检测需求;而软件补偿是在微处理器基础上,对传感器误差特性进行建模,具有补偿精度高、成本低以及通用性好等优点,可进一步提高压力传感器的精度,目前已广泛应用于传感器温度补偿中[4-6]。
软件补偿的关键在于建立高精度的传感器温度补偿模型。常用建模方法有线性回归、人工神经网络以及支持向量机等。线性回归方法简单易用,但存在模型精度差的问题;人工神经网络具有强大的自学习和非线性映射能力,建模精度高,但存在训练时间长、过学习以及易陷入局部极小等问题;支持向量机适合小样本建模,相对神经网络无局部最小点、泛化能力强,越来越广泛应用于非线性系统的建模中[7-11]。硅压阻式传感器的标定数据较少,适合采用支持向量机进行小样本建模。
本文以硅压阻式传感器温度补偿为研究对象,首先分析了经硬件补偿后的压力传感器温度漂移特性,确定了模型训练样本的选取范围,利用最小二乘支持向量机(LS-SVM)的系统回归能力和小样本建模特性,建立了传感器的温度漂移补偿模型。该方法具有简单可靠、补偿模型精度高的特点,能够有效提高传感器的精度和温度使用范围。
1 LS-SVM原理
LS-SVM是标准支持向量机(SVM)的一种改进,其将解二次规划问题转化为利用最小二乘求解线性方程组问题,求解问题的速度和收敛精度均高于标准支持向量机[12-14]。最小二乘支持向量机是损失函数为二次损失函数的支持向量机,即为误差变量。LS-SVM回归问题可表示为在约束条件下求解结构风险的最小值,即:

式中:γ为正则化参数,b为常数偏差。
式(1)是典型的条件约束优化问题,维数很高的线性回归系数优化耗时很长。将条件约束优化问题转化为其对偶空间,转换为无条件的无约束优化,可通过建立拉格朗日方程求解。引入Lagrange乘子λ,λ∈Rn×1,式(1)可转化为:
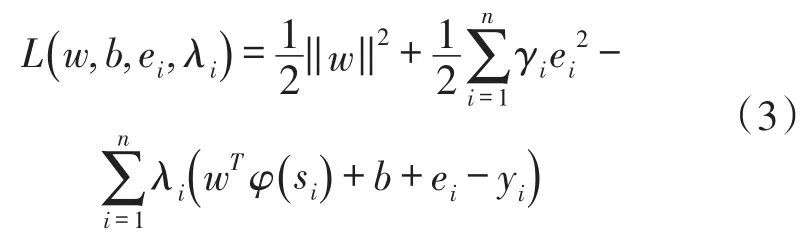
根据KKT(Karush-Kuhn-Tucker)优化条件可得到

其中,K(xi,xj)为满足 Mercer条件的核函数,
把式(4)变换为矩阵形式并消去w和e可得

求解方程(5),得到LS-SVM回归函数为
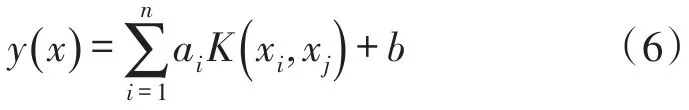
2 传感器温度补偿模型
2.1硅压阻式传感器温度漂移特性
硅压阻式传感器灵敏度与敏感单元结构由于受温度、热应力等影响,存在热灵敏度与热零点漂移,其输出电压与热漂移的关系如图1所示。其中,当压力P=0时的输出电压U0即是零点输出电压;不同温度条件下压力PN对应的输出电压UN不同。
从图1可以发现,传感器灵敏度、零点漂移与温度存在较强规律性。但经过硬件电路补偿后传感器的温度漂移特性呈现出区段化和复杂化特征,尤其是补偿区域外的传感器精度更差。建模数据选择应特别考虑补偿区域外的输出数据。
2.2传感器温度补偿原理
由于传感器对温度因素t存在交叉敏感,传感器输出电压值y与压力输入量x之间的特性方程表现为非线性函数,硅压阻式传感器的输入输出特性方程可表示为

式(7)的反函数为

获取实际的传感器输入输出关系,利用算法对传感器压力和温度数据进行温度补偿建模,可以提高传感器测量精度。其补偿原理如图2所示。

图2 硅压阻式传感器温度补偿原理
2.3基于LS-SVM的传感器温度补偿模型
2.3.1温度补偿系统组成
基于LS-SVM建立硅压阻式传感器温度补偿模型主要包括样本组建、预处理、模型训练、模型验证以及回归函数建立等,具体系统组成如3所示。

图3 基于LS-SVM的温度补偿系统系统组成
训练样本是温度补偿模型建立的基础,其蕴含了传感器温度漂移特性以及温度与压力的相关关系;LS-SVM模型训练是建立温度补偿系统的核心,包括误差惩罚因子和核函数参数的选取优化、训练模型的验证等;利用最小二乘求解线性方程组问题,从而得到非线性回归模型;回归函数是建立补偿模型的最终目的,输入测量样本通过回归模型即可对输出结果进行预测。
2.3.2训练样本组建及预处理
选择合适的训练样本可以提高训练速度和改善预测质量,训练样本的选择应覆盖整个温度和压力范围,特别是硬件温度补偿范围以外,其表现出的温度漂移才具有代表性。
压力传感器训练样本包括传感器的零点至满量程输出,范围为0 μV~80 000 μV,其范围变化较大。而核函数需要进行样本向量内积计算,对于大属性样本必然会增加计算难度,从而降低训练速度,同时减少模型对输入量的敏感,因此必须对训练样本进行归一化预处理,把样本向量归一到[0,1]区间。
设传感器压力输出为 f,fmax为最大压力输出,fmin为最小压力输出,对于压力区间内任意的压力输出,离差归一化处理方式如下:
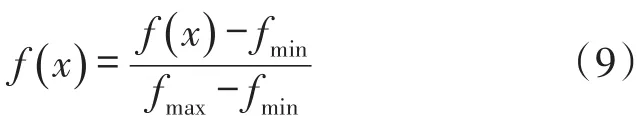
归一化的预测输出结果y′对应的实际预测值则为
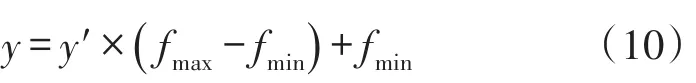
2.3.3核函数与模型参数选择
核函数是影响补偿模型实现与效果的关键因素之一。常用的核函数有多项式核函数、径向基核函数以及多层感知器核函数等。目前还没有针对具体问题选取核函数的有效方法,因此核函数的选择具有任意性[15]。径向基函数应用范围广,本文算法中的核函数采用径向基函数,即,σ为调节函数。
选取径向基核函数后,传感器温度补偿模型泛化性能和复杂度直接受正则化因子γ和核函数参数σ两个参数的影响。参数选择的常用方法有经验选择法和程序选择法。经验选择法由于选择的经验性强,常常得不到很好的建模效果。对于硅压阻式传感器LS-SVM温度补偿建模,输入参数只有压力与温度两个向量,补偿数据量少、计算纬度低。本文采用网格搜素法和交叉确认法对参数进行寻优,思路是把给定的区间划分成网格,然后在网格点上计算目标值,在比较计算与给定数据误差后,选择满足高精度建模函数对应的参数为最优值。此方法简单直观,容易理解,尤其对于选择径向基核函数的LS-SVM,每一组参数(γ,σ)都是独立的,容易实现并行计算,运行效率高。
2.3.4温度补偿模型训练步骤
采用网格搜索法进行LS-SVM的建模训练步骤如下:①首先设置γ、σ初始值;②确认γ、σ的取值范围以及步距;③检查选取的γ、σ是否满足终止条件;④如果满足条件,在所确定的γ、σ较小范围内,进行第二轮优化,重复上述步骤;⑤满足终止条件,返回γ、σ最优值;⑥利用最优值对模型进行训练验证,得到预测模型。
3 实验及结果分析
3.1传感器温度漂移数据标定
实验硅压阻式传感器采用昆山双桥传感器测控技术公司0.25级的微型压力传感器,硬件补偿温度范围为20℃~70℃。标定实验平台中气压发生泵采用美国FLUKE公司P5510-2M,压力发生范围0~2 MPa;标准数字压力表采用北京康斯特公司的ConST211,压力检测范围为0~1 MPa,精度为0.05级;温度发生装置为自制的基于半导体制冷器的加热密封腔,加热范围为0~120℃,压力传感器输出电压采用Agilent 3458A万用表进行测量。压力标定系统如图4所示。
在0~100℃温度范围内每隔10℃选取一个温度点,在0~1 000 kPa压力范围内每隔100 kPa选取一个压力点,对传感器压力输出进行标定。其中P是气压泵产生的压力,U是传感器的输出电压,标定数据如表1所示。

表1 压力传感器标定数据
根据表1标定数据绘制不同温度下的传感器零点压力输出和灵敏度温度漂移变化曲线如图5所示。其中灵敏度温度漂移变化以传感器在20℃温度点的灵敏度75 μV/kPa为基准。

图5 不同温度点下传感器输出曲线
由图5可以发现,传感器的灵敏度和零点均随着温度变化而变化,且硬件补偿后的传感器灵敏度和零点温度漂移表现较为复杂,压力输出和零点呈现出较强的非线性。根据标定数据可以计算出,在20℃~70℃范围内传感器输出综合精度为0.25%FS,与传感器出厂时的技术指标相吻合;在补偿温度范围外综合精度远低于0.25%FS,特别在100℃、1 000 kPa时传感器的输出综合精度仅为3.2%FS。
3.2传感器温度补偿实验及结果分析
3.2.1模型精度
将表1中的温度点0℃、20℃、40℃、60℃、80℃、100℃的标定数据作为训练样本,温度点10℃、30℃、50℃、70℃、90℃的标定数据作为测试样本,建立传感器温度漂移模型。采用Matlab LS-SVM工具箱,通过网格搜索法和3-交叉确认法确定模型参数。其中γ、σ赋初始值分别为10和 0.01,搜索范围分别为 0.1~30 000,0.01~600,步距分别为0.1和0.01。训练并经过测试验证,最终确定γ=60、σ=1.93,预测输出精度如图6所示,在整个检测范围内输出综合精度优于0.2%FS。

图6 预测输出精度
3.2.2非建模点补偿效果验证
为验证温度补偿模型的适应性,在温度和压力非建模点对压力传感器温度补偿效果进行实验。表2分别为补偿前和温度补偿后与标准压力值的对比效果。在温度范围为0~100℃、压力范围为0~1 000 kPa内,补偿前的满量程综合精度为3.0% FS;经过基于最小二乘向量机的温度漂移补偿后,压力检测的满量程综合精度优于0.25%FS,温度漂移得到有效抑制,提高了检测精度,同时也表明该模型具有良好的适应性。

表2 非建模点传感器温度补偿前后比较
为验证温度补偿模型的重复性,特别是硬件补偿区间外的温度点补偿效果,分别在温度点5℃、15℃、45℃、85℃、95℃对550 kPa的标准压力进行了6次重复实验。表3为不同温度条件下6次预测输出结果。其中,S为标准偏差。由表3可以看出,硅压阻式传感器预测输出数据标准偏差小于1 kPa,即重复性优于0.1%,表明基于LS-SVM的温度补偿模型具有良好的可行性。
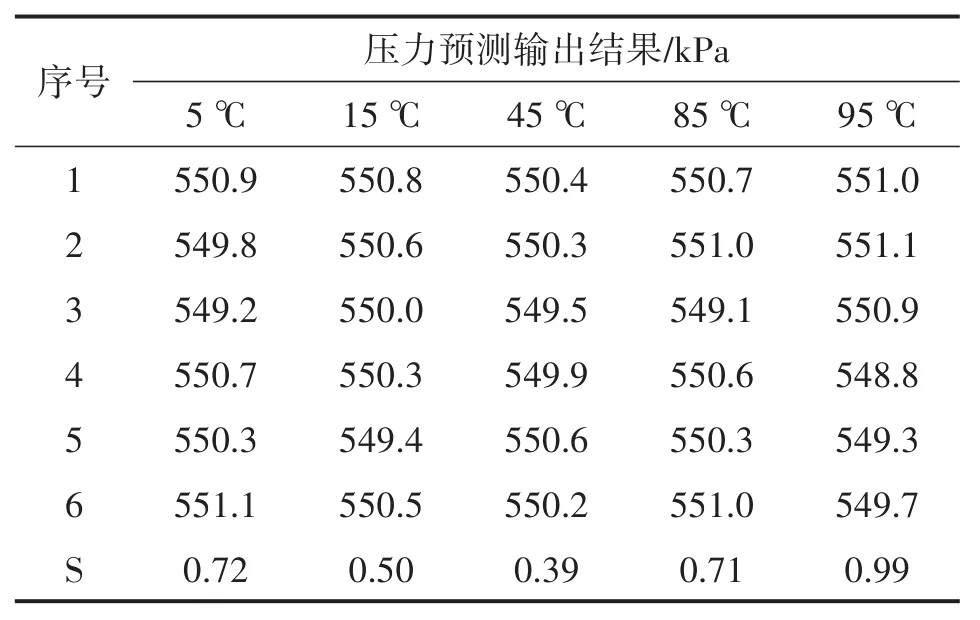
表3 温度补偿模型重复性
3.2.3采用不同算法进行建模结果的比较
为验证传感器温度补偿效果,与曲线拟合法、BP神经网络算法的模型在计算机资源耗费、预测结果精度方面进行对比。其中,曲线拟合法采用3阶函数拟合。表4为不同算法模型的训练所耗时间、预测精度对比。

表4 采用不同算法进行建模结果对比
由表3可以看出,曲线拟合法训练时间最短,但预测精度最差;而LS-SVM的训练时间只有BP算法的1/3,预测精度却高于BP算法。综合上述结果表明,LS-SVM模型相对其它2种方法具有训练时间短、精度高的优点。
4 结论
本文分析了温度对传感器灵敏度和零点输出的影响,选取了径向基核函数,通过网格搜索法和交叉确认法对模型参数进行了优化,建立了基于LS-SVM的传感器温度漂移补偿模型,降低了传感器对温度的敏感度。实验结果表明,在小样本检测数据的条件下,基于LS-SVM的传感器温度补偿方法能够有效提取温度漂移的非线性特征,温度补偿模型在0~100℃范围内把传感器输出综合精度从3.2%FS提高到0.25%FS,进一步提高了传感器的精度和温度使用范围,具有较高的实用价值。
[1] 郭冰,王冲.压力传感器的现状与发展[J].中国仪器仪表,2009(5):72-75.
[2] 李玉华,李永飚,马林.传感器温度补偿技术[J].精密制造与自动化,2015(1):47-51.
[3] 刘鹏,杨学友,杨凌辉,等.基于MAX1452硅压力传感器温度补偿系统的设计[J].仪表技术与传感器,2010(4):61-64.
[4] 鞠文斌,于洪峰,吴亚林.宽温度压阻式传感器的热灵敏度漂移补偿[J].传感器技术,2002,21(5):43-45.
[5] 胡园园,李淮江,王大军.基于ATmega16的压力传感器温度补偿智能化设计[J].仪表技术与传感器,2010(10):8-11.
[6] 王俊杰,秦会斌.压力传感器高精度温度补偿的软件实现[J].现代电子技术,2014,37(22):105-107,110.
[7] Futane N P,Roy Chowdhury S,Roy Chowdhury C,et al.Analog ASIC for Improved Temperature Drift Compensation of a HighSensitive Porous Silicon Pressure Sensor[J].Analog Intergrated Circuits and Signal Processing,2011,67(3):383-393.
[8] 轩春青,轩志伟,陈保立.基于最小二乘与粒子群算法的压力传感器动态补偿方法[J].传感技术学报,2014,27(10):1363-1366.
[9] 赵海鹰.压力传感器非线性曲线拟合方法及不确定度分析[J].计测技术,2014,34(4):74-76.
[10]孙艳梅,苗凤娟,陶佰睿.基于PSO的BP神经网络在压力传感器温度补偿中的应用[J].传感技术学报,2014,27(3):342-346.
[11]朱永强,田军.最小二乘支持向量机在光伏功率预测中的应用[J].电网技术,2011,35(7):54-59.
[12]Vapnik V N.An Overview of Statistical Learning Theory[J]. IEEE Trans Neural Network,1999,10(5):988-999.
[13]陈爱军.最小二乘支持向量机及其在工业过程建模中的应用[D].杭州:浙江大学信息科学与工程学院,2006.
[14]Suykens J A K,Vandewalle J.Recurrent Least Squares Support Vector Machines[J].IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Applications,2000,47(7):1109-1114.
[15]肖建,于龙,白裔峰.支持向量回归中核函数和超参数选择方法综述[J].西南交通大学学报,2008,43(3):297-303.

杨遂军(1979-),男,硕士,实验师,主要研究方向为化工产品安全测试技术与仪器,量热技术与仪器,yangsuijun1@sina.com;

叶树亮(1973-),男,博士,教授,主要研究方向为化工产品安全测试技术与仪器、工业零部件缺陷检测技术与设备、精密测量中部件信号处理与误差分析技术,itmt_paper@126.com。
Temperature Compensation of Silicon Piezoresistive Sensor Based on Least Square-Support Vector Machine*
YANG Suijun,KANG Guolian,YE Shuliang*
(Institute of Industry and Trade Measurement Technology,China Jiliang University,Hangzhou 310018,China)
Aiming at the problems of the large sensitivity and zero temperature drift of the silicon piezoresistive sensor using hardware compensation,a new method based on the least square-support vector(LS-SVM)is adopted to construct the temperature compensation model.In this paper,the temperature drift property of the silicon piezoresistive sensors which have been compensated by hardware are analyzed,and data with the uniform distribution of the whole temperature and pressure range is selected to be as the model input and is preprocessed to train the output data.The kernel and regularization parameter of the model is optimized by using the grid searching method and the cross-validation method,and a temperature compensation model of the sensor is established.Experiment results show the comprehensive accuracy is improved from 3.2%up to 0.25%in the temperature range of 0~100℃by temperature compensation model based on LS-SVM,this method further improves the accuracy and temperature application range and can be put to good use.
silicon piezoresistive sensor;temperature drift;temperature compensation;least square-support vector machine(LS-SVM)
TP212
A
1004-1699(2016)04-0500-06
项目来源:浙江省科技厅公益技术研究社发项目(2014C33114)
2015-10-21修改日期:2016-01-11

