Digital Relief Generation from 3D Models

WANG Meili, SUN Yu, ZHANG Hongming, , QIAN Kun, CHANG Jian, and HE Dongjian



Digital Relief Generation from 3D Models

WANG Meili1, SUN Yu1, ZHANG Hongming1,*, QIAN Kun2, CHANG Jian2, and HE Dongjian3

1 College of Information Engineering, Northwest A & F University, Yangling 712100, China;2 National Center for Computer Animation, Bournemouth University, Poole BH12 5BB UK;3 College of Mechanical and Electronic Engineering, Northwest A & F University, Yangling 712100, China

It is difficult to extend image-based relief generation to high-relief generation, as the images contain insufficient height information. To generate reliefs from three-dimensional (3D) models, it is necessary to extract the height fields from the model, but this can only generate bas-reliefs. To overcome this problem, an efficient method is proposed to generate bas-reliefs and high-reliefs directly from 3D meshes. To produce relief features that are visually appropriate, the 3D meshes are first scaled. 3D unsharp masking is used to enhance the visual features in the 3D mesh, and average smoothing and Laplacian smoothing are implemented to achieve better smoothing results. A nonlinear variable scaling scheme is then employed to generate the final bas-reliefs and high-reliefs. Using the proposed method, relief models can be generated from arbitrary viewing positions with different gestures and combinations of multiple 3D models. The generated relief models can be printed by 3D printers.The proposed method provides a means of generating both high-reliefs and bas-reliefs in an efficient and effective way under the appropriate scaling factors.

high-relief, bas-relief, mesh enhancement, scaling

1 Introduction

Reliefs are sculptured artworks in which a modeled shape is raised or lowered and usually attached to a planar background[1]. There are three main types of relief: high-reliefs, bas-reliefs, and sunken-reliefs. In a high-relief, the raised sculpture is over 50% of the scale height of the image being represented. Bas-reliefs, by comparison, are much more compressed, and are suitable for scenes with many figures, landscapes, or architectural backgrounds. In sunken-reliefs, the figures are actually carved into the surfaces.

Existing relief models created by artists involve complex procedures. Once the relief models have been produced, they are not easy to modify or maintain. Such reliefs also only represent a single viewing point. However, animators and artists prefer a digital relief—an object having the characteristics of a real relief, but with the advantages of being virtual. There are many 3D models in the public domain that could be processed into reliefs that are easily amended and refined. A system to produce digital reliefs must allow for interactive design and generate standard 3D relief representations.

Previous relief generation research has mainly considered bas-relief generation, which is very challenging. For example, generating a bas-relief requires a 3D model to be compressed into an almost flat plane while preserving the details of the image and avoiding any distortion of the shapes.

The general approach is to start with height field data or a 3D model, and then apply image processing techniques to produce the relief[2]. In this paper, we propose a method to simultaneously generate digital high-reliefs and bas-reliefs by setting different scaling factors. We develop a boosting algorithm with different smoothing schemes to enhance the geometrical details, and employ a nonlinear method to scale the 3D meshes while preserving their features[3].

The remainder of this paper is organized as follows. Section 2 reviews related work, both for image-based and model-based techniques. Then a detailed mesh enhancement and relief generation method is presented in section 3. The output given by our method and the results of a parameter test are presented in section 4. We conclude the paper in section 5 with a discussion of some of the advantages and limitations of our approach.

2 Related Work

Reliefs can be generated by direct modeling, images, and 3D models. Direct modeling requires special expertise and is a labor-intensive process.

2.1 Bas-relief generation from images

A method of generating bas-reliefs from a pair of input images using an iterative least-squares optimization to reconstruct the relief surfaces proposed by ALEXA and MATUSIK[4].

An algorithm for bas-relief generation from 2D images with gradient operations, such as magnitude attenuation and imageenhancement, greatly improved the quality of therelief[5]. A novel method for the digital modeling of bas- reliefs from a composite normal image was presented by JI, et al[6], who composed several layers of normal images into a single normal image. An image-based relief generation method was designed especially for brick and stone reliefs, providing a two-level approach for estimating the height map from single images, with a mesh deformation scheme and normal computation. However, it is difficult to extend image-based relief generation to high-relief generation, as the images contain insufficient height information and the computation time is much greater[7].

2.2 Model-based relief generation

A computer-assisted relief generation system was developed by CIGNONI, et al[8], who applied a compression that is inversely proportional to the height value followed by a linear rescaling to generate 3D bas- and high-reliefs from 3D models.

Clearly, reliefs generated from 3D objects are considered to be a promising means of creating bas-reliefs, and also allow for the reuse of existing 3D models. The final generated reliefs convey real height information, which could easily be machined directly into real reliefs. Furthermore, the generated 3D reliefs can be edited and modified before real machining. The challenge is to retain the fine details of a 3D object while greatly compressing its depths to produce an almost planar result. To achieve the highest-quality results, it is important that the sharpness, richness of detail, and accuracy is taken into account. Existing techniques use different feature-preserving methods to generate bas-relief models with rich details, even with high compression ratios[9–12].

An improved relief generation method proposed by KERBER, et al[13]added a user interface and implemented the algorithm on graphics hardware. This allowed the generation of real-time dynamic reliefs given an animated model.

A series of gradient-based algorithms have been proposed by ZHANG, et al[14], including height field deformation, high slope optimization, and fine detail preservation. These can be used to generate bas-reliefs interactively. Recently, a unified framework presented by SCHULLER, et al[15]created bas-reliefs from target shapes, viewpoints, and space restrictions.

Most of the methods mentioned above first convert 3D models into height fields, which can only generate bas-reliefs.A method proposed by ARPA, et al[16]synthesized high-reliefs using differential coordinates. High-relief synthesis is semi-automatic, and can be controlled by user-defined parameters to adjust the depth range and the placement of the scene elements with respect to the relief plane. Our proposed method can generate both high-reliefs and bas-reliefs from 3D models with high efficiency, making it computationally feasible to obtain different viewpoints under different gestures of a single model, and also to combine models together to generate more multiple relief models.

3 Mesh Enhancement and Relief Generation

Meshes can be represented in a number of methods using different data structures to store the vertex, edge, and face data. Among those methods, the Face-Vertex mesh, which represents an object as a set of faces and a set of vertices, is widely used for mesh representation[17]. The method proposed in this paper is based on a Matlab toolbox provided by GABRIEL[18]. In this platform, vertexes store the 3D vertex positions and faces store 3-tuples giving the number of vertices forming faces as two matrixes.

When a 3D mesh is provided, the algorithm first enhances the mesh using 3D unsharp masking (USM), which flattens the mesh while preserving its details.

3D USM is implemented by a simple smoothing scheme. The smoothed mesh is subtracted from the original mesh to extract the mesh’s higher-order features. These features can be enhanced by scaling them and adding them back into the original mesh[19]. After enhancing the features, a proportional nonlinear scaling scheme is adopted to produce the final bas-reliefs and high-reliefs with different scaling factors.

3.1 Unsharp masking

USM is a feature-enhancement technique in image processing that splits a signal into low- and high-frequency components. An input image is convolved with a low-pass kernel, resulting in a smooth version of the input image. Subtracting the smooth version from the original image leads to a high-frequency image containing peaks at a small-scale level of detail. Adding a multiple of the high-frequency image back into the smooth image emphasizes the fine structures in the newly reassembled image.

3D USM is an extension and derivative of 2D USM. Its main function is to extract the mesh’s higher-order features. In the 3D case,

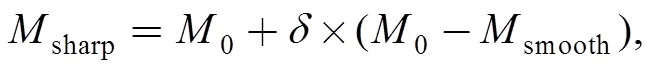
wheresharpis the sharpened mesh,0is the base mesh,smoothis the smoothing mesh with different smoothing strategies, andis the amount of enhancement. The adjustment ofcan be used for artistic control.

3.2 Mesh smoothing strategies

The simplest approach is average smoothing, which is widely used in image processing. It replaces each vertex with the average of its one-ring vertices. Average smoothing is straightforward to implement and has high computational efficiency, but can cause blurring. It is expressed as

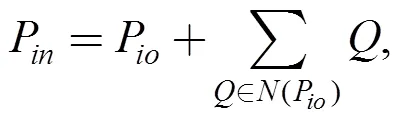
wherePis an updated vertex ofP,Pis the original vertex ofP, and(P) are the one-ring neighbors ofP.

Laplacian smoothing changes the node positions without modifying the topology of the mesh. It is simple to implement, because a given vertex only requires information about its immediate neighbors. For each vertex in a mesh, a new position is chosen based on local information, and the vertex is gradually moved there. There are a number of different approximations for the Laplacian operator, and each has a particular use[20–21]. The discrete approximation can be described as

wherewis the weight for the edge with end points (x, x). There are several schemes for defining the weightsw: combinatorial, distance, and conformal weights. The combinatorial weight is an adjacency matrix, and any arbitrary edge weight is the Euclidean distance of the two faces connected by the edges.

The distance weight is the nonlinear operator:

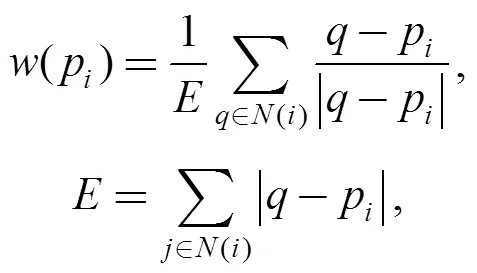
In the conformal weight approach, for a mesh with triangular faces and verticesv,v,v, the angle between edge (v,v) and edge (v,v) can be expressed as angle (vv,vv), so(,) can be calculated as

In Eq. (5), vertexesvandvbelong to one-ring neighbors of vertexv. This weight scheme smooths the mesh while preserving its shape, minimizing potential distortion related to angle changes. Laplacian smoothing can be applied iteratively to obtain the desired mesh smoothness. In the experiments described in this paper, the conformal weight approach has been applied.

3.3 Nonlinear scaling scheme

To scale 3D meshes efficiently, a nonlinear scaling should be used instead of linear scaling, because linear scaling cannot distinguish the important parts of the mesh. The objective is to scale the height of the relief proportional to the height field. To generate a relief, the higher part of the object should be scaled more than the lower part to preserve the features. An attenuation function can be used for this purpose[3]:

The scaling factorcontrols the depth compression ratio, with larger values signifying less compression. For bas-relief generation, a small value is chosen to present the model in a nearly flat plane, whereas for high-relief, a relatively large value is applied.also defines the level of preservation of details, where a small value would smooth out small depth changes in the model. The parameterdetermines the degree to which the height has changed. Larger heights are scaled more (assuming 0<<1). Choosing=0.1and=0.9 gives the scaling suggested by FATTAL, et al[3].

4 Results of Relief Generation

4.1 High-reliefs

In high-reliefs, the height is over half of the natural depth of the surface. Therefore, according to the definition in section 3.3, SF is greater than 0.5.

We use the Armadillo model as an example to illustrate the results of the algorithm. For high-relief generation, we set=0.2 and examined the output with=0.7,=0.6, and=0.5. All testing models were taken from Aim Shape.

It can be seen from Fig. 1 that the higher value of(0.7) preserves more features, although the overall details are preserved for all. The influence ofwill be examined in section 4.4.

4.2 Bas-relief

In bas-reliefs, the height is less than half of the natural depth. Recent studies have assumed a compression ratio of 0.02. Fig. 2 demonstrates the bas-reliefs of the Armadillo models generated by the proposed method with=0.2 and=0.02. The mesh enhancement techniques and nonlinear scaling scheme effectively preserve the details of the models in bas-relief.

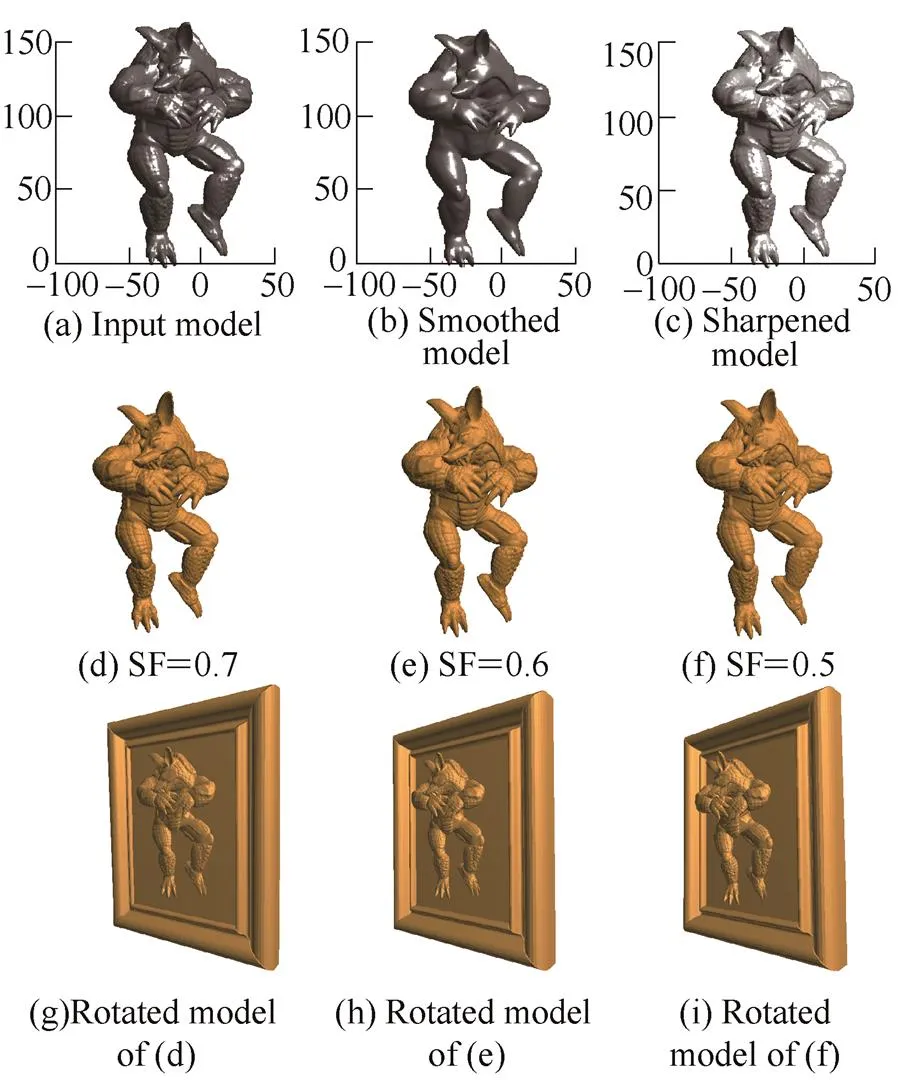
Fig. 1. High-reliefs with Armadillo model

Fig. 2. Armadillo bas-relief generated by the proposed algorithm

Fig. 3 presents examples showing the performance of the proposed algorithm on Raptor and Ball models. It can be seen that bas-reliefs are generated in which the details have been preserved.

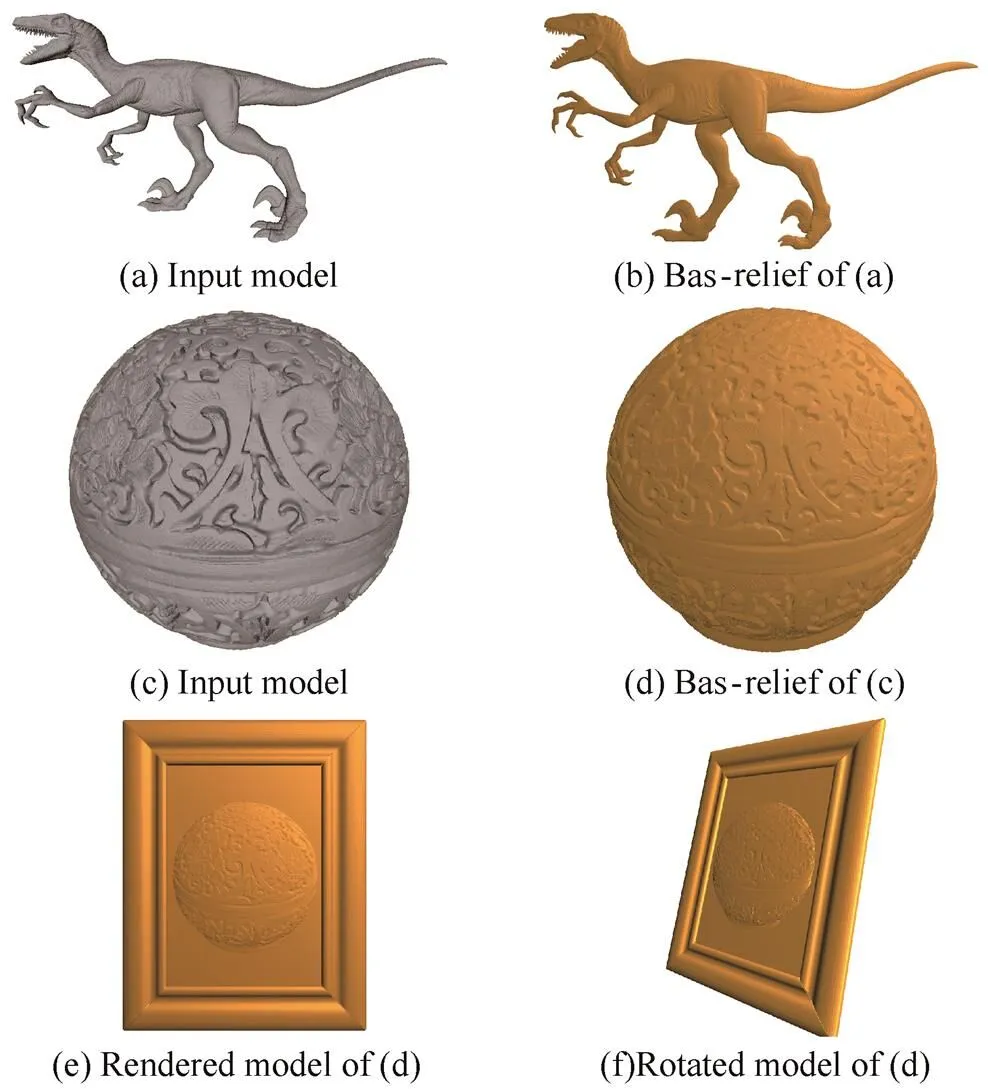
Fig. 3. Bas-reliefs with different models

4.3 Multiple views and multiple models

It is straightforward to apply different viewing angles under different gestures to the original model, because the proposed method operates directly on 3D meshes. For example, adjusting the original model to different viewpoints under different gestures and then applying the proposed algorithm generates bas-reliefs with different view angles. An example with the Armadillo model is shown in Fig. 4.

Fig. 4. Bas-reliefs with different poses of a single model

An extension of the proposed method is the generation of complex combined relief models. The use of different models of a meaningful scene to generate multiple models is illustrated in Fig. 5 and Fig. 6. The proposed method has a relatively low computation time, with the combination of Raptor and Ball requiring about 50 s to get the final relief models.

Fig. 5. Example of bas-reliefs with multiple models

Fig. 6. Another example of bas-reliefs with multiple models

Fig. 7. Two smoothing strategies results

We now find the parameter that most strongly influences the results and determine its appropriate value. The test case will be on bas-relief generation of the Skull model. The results for various enhancement levelsare as follows.

It can be seen from Fig. 8 that, asincreases, the relief models are enhanced. However, largervalues result in undesired deformation when applied to 3D USM. In a generic USM, the high-frequency part is linearly scaled by a specified factor and added back into the original. A suitable factor, in this case, must be chosen carefully, because artifacts are triggered by a largerin the final bas-relief generation, as seen in Fig. 8. Aesthetically pleasing results are produced with=0.2.

Fig. 8. Differentfrom 0.2 to 1.0

4.5 3D printing

A Projet 3510 SD was used to print some of our bas-relief models to validate the effectiveness of our proposed method. The results are shown in Fig. 9. The 3D printer mesh volume was 298 mm´185 mm´203 mm, the resolution was 345 DPI´375 DPI´790 DPI, the precision was 0.025–0.05mm, and the material was Visi–Jet M3 X. The size of the 3D bas-reliefs produced by this method was 100 mm´150 mm´5 mm.

Fig. 9. 3D printed models

5 Conclusions

(1) To preserve the original details in both high-reliefs and bas-reliefs, USM and a nonlinear scaling scheme are developed and implemented.

(2) It is relatively easy to implement the proposed method, because it operates directly on 3D meshes. Furthermore, it is amenable to relief generation from multiple viewpoints under different gestures of the original model, and can also be extended to relief generation by multiple models.

(3) A physical 3D prototype can be produced by 3D scanners to satisfy artistic necessities.

[1] FLAXMAN J, WESTMACOTT R.[M]. Whitefish MT: Kessinger Publishing, 1838.

[2] KERBER J, TEVS A, BELYAEV A, et al. Feature sensitive bas relief generation[C]//Beijing, China, June 26–28, 2009: 148–154.

[3] FATTAL R, LISCHINSKI D, WERMAN M. Gradient domain high dynamic range compression[J]., 2002, 21(3): 249–256.

[4] ALEXA M, MATUSIK W. Reliefs as images[J]., 2010, 29(4): 157–166.

[5] WANG M L, CHANG J, PAN J J, et al. Image-based bas-relief generation with gradient operation[C]//, Innsbruck, Austria, February 17–19, 2010: 679–686.

[6] JI Z P, MA W Y, SUN X F. Bas-relief modeling from normal images with intuitive styles[J]., 2014, 20(5): 675–685.

[7] LI Z, WANG S, YU J, et al. Restoration of brick and stone relief from single rubbing images[J]., 2012, 18(2): 177–187.

[8] CIGNONI P, MONTANI C, SCOPIGNO R. Computer-assisted generation of bas- and high- reliefs[J]., 1997, 2(3): 15–28.

[9] KERBER J, WANG M L, CHANG J, et al. Computer assisted relief generation—A survey[J]//. Blackwell Publishing Ltd, 2012, 31(8): 2363–2377.

[10] SONG W, BELYAEV A, SEIDEL H P. Automatic generation of bas-reliefs from 3D shapes[C]//, Lyon, France, June 13–15, 2007: 211–214.

[11] SUN X, ROSIN P L, MARTIN R R, et al. Bas-relief generation using adaptive histogram equalization[J]., 2009, 15(4): 642–653.

[12] WEYRICH T, DENG J, BARNES C, et al. Digital bas-relief from 3D scenes[J]., 2007, 26(3): 32–39.

[13] KERBER J, TEVS A, ZAYER R, et al. Real-time generation of digital bas-reliefs[J]., 2010, 7(4): 465–478.

[14] ZHANG Y W, ZHOU Y Q, LI X L, et al. Bas-relief generation and shape editing through gradient-based mesh deformation[J]., 2015, 21(3): 328–338.

[15] SCHULLER C, PANOZZO D, SORKINE-HOMUNG O. Appearance-mimicking surfaces[J].2014, 33(6): 216–226.

[16] ARPA S, SUSSTRUNK S, HERSCH R D. High Reliefs from 3D Scenes[J]//, 2015, 34(2): 253–263.

[17] TOBLER R F, MAIERHOFER S. A mesh data structure for rendering and subdivision[C]//, Plzen, Czech Republic, 2006: 157–162.

[18] GABRIEL P—[EB/OL]. Cnrs, Ceremade, Universite Paris- Dauphine, 2008(2016-02-15). http://www.ceremade.dauphine.fr/~ peyre/matlab/graph/content.html.

[19] LUFT T, COLDITZ C, DEUSSEN O. Image enhancement by unsharp masking the depth buffer[J]., 2006, 25(3): 1206–1213.

[20] DESBRUN M, MEYER M, SCHRODER P, et al. Implicit fairing of irregular meshes using diffusion and curvature flow[C]//, New Orleans, Lousiana, USA, July 23–28, 2000: 317–324.

[21] WANG L, HE X, LI H. Development of a percentile based three-dimensional model of the buttocks in computer system[J]., 2016, 29(3): 633–640.

Biographical notes

WANG Meili, born in 1982, is currently an associate professor at. She received her PhD degree from, in 2011. Her research interests include computer-aided design, image processing, and 3D modeling.

Tel: +86-29-87091249; E-mail: meili_w@nwsuaf.edu.cn

SUN Yu, born in 1994, is currently a graduate candidate at. He received his bachelor’s degree fromin 2016. His research interests include computer animation, games, and 3D modeling. Tel: +86-150-2903-0583; E-mail: 625559029@qq.com

ZHANG Hongming, born in 1979, is currently an associate professor at. He received his PhD degree fromin 2012. His research interests include spatial big data analysis, soil erosion mapping, and digital terrain analysis.

Tel: +86-29-87091249; E-mail: zhm@nwsuaf.edu.cn

QIAN Kun, born in 1986, is currently a PhD candidate at. He received his master’s degree in computer science fromHis research mainly focuses on physics-based animation, deformation simulation, collision detection, haptic rendering, and virtual surgery.

Tel: +44-01202962249; E-mail: Kqian@bournemouth.ac.uk

CHANG Jian, born in 1977, is currently an associate professor at. He received his PhD degree in computer graphics in 2007 from the. His research focuses on a number of topics related to geometric modeling, algorithmic art, character rigging and skinning, motion synthesis, deformation and physical-based animation, and novel human computer interaction. He also has a strong interest in applications in medical visualization and simulation.

Tel: +44-0781-4891106; E-mail: jchang@bournemouth.ac.uk

HE Dongjian, born in 1957, is currently a professor at the. He received his PhD degree from,in 1998. His research interests include image analysis and recognition, intelligent detection and control, multimedia networks, and virtual reality.

Tel: +86-153-3249-1226; E-mail:hdj168@nwsuaf.edu.cn

Received May 12, 2016; revised July 15, 2016; accepted July 20, 2016

Supported by National Natural Science Foundation of China(Grant Nos. 61402374, 41301283), National Hi-tech Research and Development Program of China(863 Program, Grant No. 2013AA10230402), and China Postdoctoral Science Foundation

© Chinese Mechanical Engineering Society and Springer-Verlag Berlin Heidelberg 2016

10.3901/CJME.2016.0720.084, available online at www.springerlink.com; www.cjmenet.com

E-mail: zhm@nwsuaf.edu.cn