多谐差相信号在伺服系统频率特性测试中的应用*

朱燕梅，侯文，张寅

（1.中北大学仪器与电子学院，太原030051；2.中北大学信息与通信工程学院，太原030051）

多谐差相信号在伺服系统频率特性测试中的应用*

朱燕梅1，侯文2*，张寅1

（1.中北大学仪器与电子学院，太原030051；2.中北大学信息与通信工程学院，太原030051）

为了减少伺服系统频率特性测试的测试时间，提高测试精度，选用非均匀功率谱的多谐差相信号作为激励源。该信号具有较低的峰值因子，还可以使激励更加平稳均匀。以某型舵机为例进行实验，结果表明，其测试精度与传统的正弦扫描信号作为激励的情形相比，幅频特性的误差保持在±0.069 dB以内，相频特性的误差保持在±0.602°以内，测试时间减少53.3%，在测试过程中系统运行平稳，适合频率特性的快速高精度测试。

伺服系统；频率特性测试；多谐差相信号；峰值因子

伺服系统又称为随动系统［1］，频率特性是其重要特性之一。通过对伺服系统的频率特性的测试可以判断某些参数或环节对系统性能的影响，因而频率特性测试对于伺服系统的研究、分析、改进以及故障检测等方面都具有重要的意义［2-5］。

伺服系统频率特性测试的输入信号有正弦扫描信号、多频声信号等。传统的正弦逐点扫描法每次只输入一个频率的正弦信号，得到对应的频率响应，该方法测试精度高，但测量时间长；多频声信号作为输入信号时与传统方法相比测试精度基本相同，测试时间显著提高，但是多频声信号波动较大，会使系统变得不稳定，甚至损坏系统［6-7］。非均匀功率谱的多谐差相信号具有带宽和频谱可以精确设定、无杂散频率成分的优点［8］，而且具有比多频声信号更小的峰值因子。

1　多谐差相信号

多谐差相信号SPHS（Schroeder Phased Harmonic Sequence）是由若干个功率、周期、初相有一定关系的正弦信号叠加而成的周期性信号［9］。多谐差相信号的一般数学表达式为

式中，N为叠加的谐波的个数，T是信号的基波周期，θk是第k次谐波的相角，Pk是第k次谐波的相对功率，且若第k次谐波的功率为pk，则第k次谐波的相对功率定义为

多谐差相信号的相位解析式，被称为“Schroeder相位编码准则”，该准则是基于Woodward定理推导出来的。该准则作为调整多频正弦信号相位的主要方法，沿用至今［10］。峰值因子的定义为

其中，M+和M-分别表示x（t）中的最大正波峰值和最大负波峰值，Eeff为信号x（t）的有效值

如果选定Pk，就是如何选择θk使得M+-M-最小，使得峰值因子（CF）最小。

设某一余弦信号的相位是ϕ（t）且是线性的，即

式中

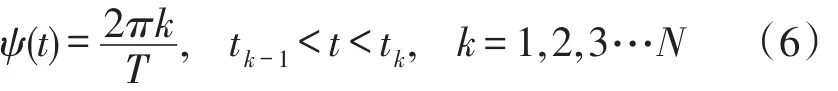
其中，当k=0时，由于P0不存在，故t0=0。

令

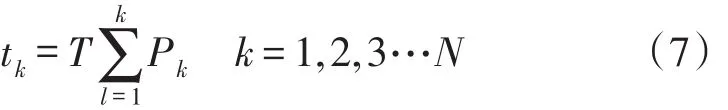
式中，tk是相位改变时刻［11］。在该时刻，瞬时频率改变了该信号的相位。由式（7）可得在时间间隔tk-tk-1内信号的瞬时频率等于k/T，tk-tk-1正比于第k次谐波的相对功率Pk。

该信号在第n个时间段内的瞬时相位是

当上述表达式中的谐波数N≥1时，φn是该信号第n次傅立叶分量的常数项。由相位连续性可得，ϕ（t）在t=tk-1处是相等的，即

或者

把式（7）代入上式可得

由式（13）可得斯克罗德相位编码准则最终解析式

采用多谐差相信号作为输入信号有以下优点［12］。①该信号能够一次性地激励系统以使其显现出在各个频率处的特征，能够明显缩短测试时间；②它具有离散的频谱，可以抑制大部分的噪声干扰，测试精度高；③该信号具有比多频声信号更小的峰值因子，信号的能量分布更加均匀，将该信号作为频率特性的输入信号更有利于测试。

2　非均匀功率谱多谐差相信号与多频声信号的比较

峰值因子可以用来作为衡量信号波动幅度大小和激励是否平稳均匀的标准，普通正弦信号的这在频率特性测试中是最理想的情况，选择合理的相位叠加方式生成的多频正弦信号的峰值因子越接近该信号就越适合作为频率特性测试的输入信号。

将具有非均匀功率谱的多谐差相信号与多频声信号对比，多频声信号的相位合成方式选择零相位差和线性相位差两种方式，多频声信号的数学表达式为

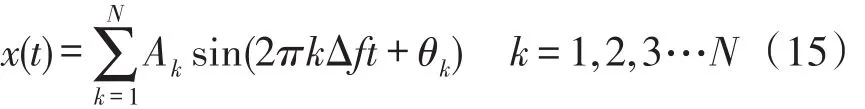
幅值Ak=1V，频率间隔都为Δf=1，谐波个数N=10，各谐波初相位均为0生成的多频声信号如图1所示。

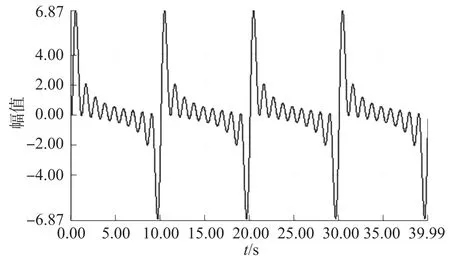
图1　零相位差的多频声信号波形图

由图1得初始相位都为零生成的多频正弦信号的最大值为6.87 V，在某些时刻信号的峰值远远超过1 V，信号的波动幅度很大，不适合作为频率特性测试的输入信号。

依据线性相位差叠加，即令

生成的多频声信号波形图如图2所示。

图2　根据线性相位差叠加的多频声信号

图2按线性相位差生成的多频声信号在各个频率点能量分布相对均匀，没有大的尖峰脉冲，是多频声信号中峰值因子最小的情况，比较适合作为频率特性测试的输入信号。

设多谐差相信号具有以下的非均匀功率谱，即

令N=16，生成的多谐差相信号如图3所示。

图3　非均匀功率谱的多谐差相信号的波形图及频谱图

由图3得非均匀功率谱的多谐差相信号的能量更加均匀地分布在各个频率点，信号幅值更加平稳均匀，具有比多频声信号更小的峰值因子，更适合作为系统频率特性测试的激励信号。

各信号的峰值因子如下表1所示。

通过以上对比得选择具有非均匀功率谱的多谐差相信号作为伺服系统频率特性测试的输入信号与多频声信号相比，测试结果在保证精度高和测试时间短的情况下，激励更加平稳均匀，十分有利于测试。

表13　种信号的峰值因子

3　实验分析

为验证前述输入信号的选择对实际测试结果的影响，该实验将具有非均匀功率谱的多谐差相信号以某型导弹伺服舵机系统为测试对象进行实验研究，采用FFT法对频率特性测试的数据进行处理。

分别采用3种不同的信号作为系统频率特性测试的输入信号，正弦扫描信号作为输入信号时，幅值为1 V；根据线性相位差进行叠加的多频声信号的幅值为1 V，测试时N=10；基于非均匀功率谱的多谐差相信号输入信号幅值测试时N=10，3种信号测试时的频率范围都为0.1 Hz～100 Hz。在实际测试时由于非均匀功率谱多谐差相信号的幅值比较小，所以将信号的幅值放大3倍。

测试时激励信号分为3段，其中第1段频率范围为0.1 Hz～1 Hz，周期数为1，频率间隔为0.1 Hz，采样周期10ms；第2段频率范围为1 Hz～10 Hz，周期数为3，频率间隔为1 Hz，采样周期1 ms；第3段频率范围为10 Hz～100 Hz，周期数为4，频率间隔10 Hz，采样周期0.1 ms。进行多次实验，取其中的任意一次实验的频率特性曲线如图4所示。

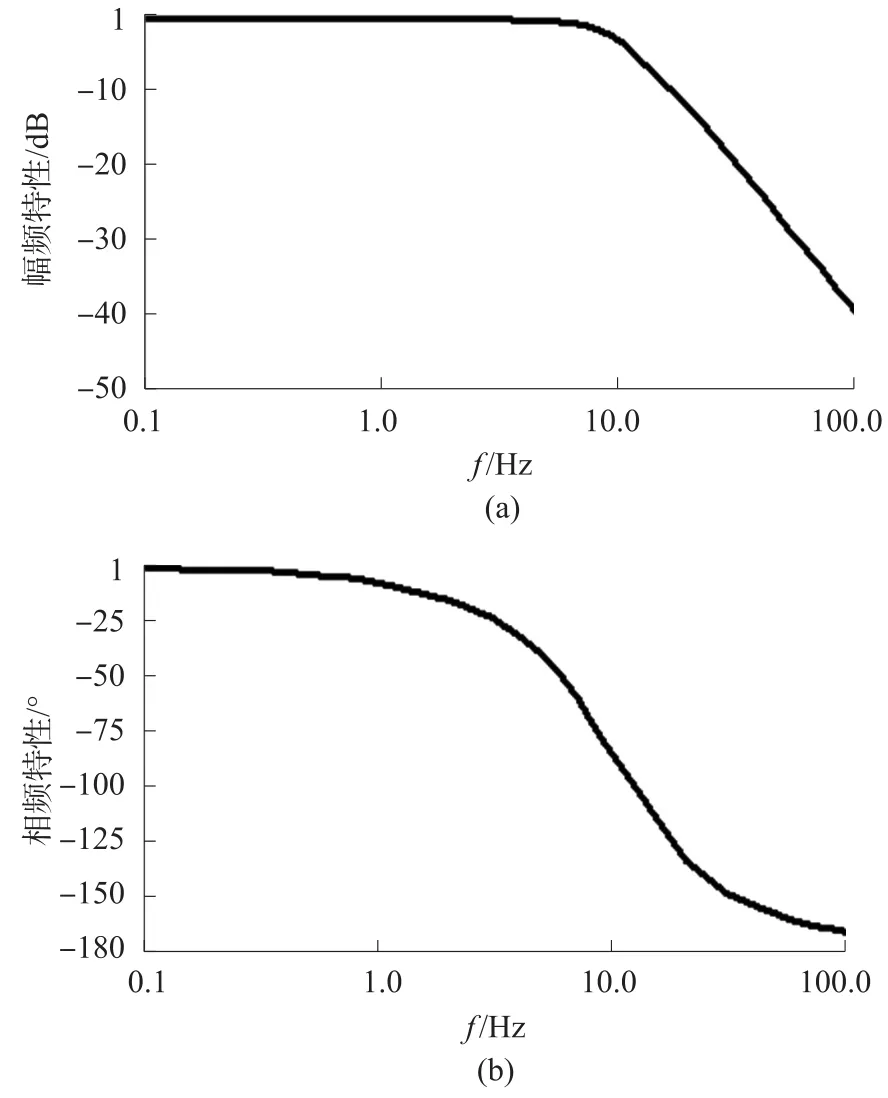
图4　非均匀功率谱的多谐差相信号作为输入的频率特性曲线

以正弦扫描信号测试结果为准，非均匀功率谱的多谐差相信号作为输入信号多次实验测得的误差值如表2所示。

表2　2种不同信号输入时的测试误差

将以非均匀功率谱的多谐差相信号作为频率特性测试的输入信号与传统的正弦逐点扫信号比较，计算后发现基于非均匀功率谱的多谐差相信号测得的幅频特性的误差保持在±0.069 dB以内，相频特性的误差保持在±0.602°以内；正弦扫描法的测试时间大约为30 s，基于非均匀功率谱的多谐差相信号的测试时间大约为14 s。结果表明选用该信号对频率特性进行测试有足够高的精度，测试时间大约减少了53.3%。而且，与多频声信号在进行频率特性测试时相比，观察到前者作为激励时系统运行更加平稳。由此可见多谐差相信号能更好的满足频率特性的快速高精度测试要求。

4　结束语

对实际系统的测试结果表明，用非均匀功率谱的多谐差相信号作为伺服系统频率特性测试的输入信号，与传统的正弦扫描法相比显著地提高了测试速度；由于该信号有效的解决了峰值因子的问题，波形波动幅度更小，与多频声信号相比，保证测试过程中激励平稳均匀。以该信号作为输入信号可以实现频率特性的快速、精确测量，且测试过程易于实现。

［1］王刚.直流电机伺服控制技术研究与实现［D］.大连：大连理工大学，2013.

［2］白瑛，贺召卿，周长义，等.基于线性运算功放模块PWM直流伺服系统设计与实现［J］.电子器件，2006，29（1）：272-274.

［3］张寅，侯文，李建民.基于Multitone信号的伺服系统频率特性测试方法研究［J］.计算机测量与控制，2014，22（10）：3129-3131.

［4］刘艳云，朱雷.基于MSP430单片机和DDS技术的频率特性测试仪的设计［J］.电子器件，2011，34（5）：521-524.

［5］肖定邦，侯占强，谢立强，等.基于二次谐波检测的电容式微惯性［J］.传感技术学报，2009，22（1）：70-74.

［6］沈伟，兰山.伺服系统频率特性测试方法研究［J］.实验技术与管理，2011，28（11）：268-271.

［7］何春华，崔健，闫俊杰，等.基于LabVIEW的微机械陀螺自动测试系统开发［J］.传感技术学报，2011，24（2）：170-174.

［8］侯国屏，吴静，董甲瑞.Multitone信号及其在测量中的应用［J］.清华大学学报，2007，47（10）：1574-1577.

［9］张笑可，张胜修，王楠.基于多谐差相信号的某型导弹舵机系统测试方法研究［J］.弹箭与制导学报，2009，29（3）：77-79.

［10］Schroeder M R.Synthesis of Low-Peak-Factor Signals and Binary Signals with Low Autocorrelation［J］.IEEE Trans Informarion Theory，1970：85-89.

［11］van den Bos A，Krol R G.Synthesis of Discrete-Interval Binary Signals with Specified Fourier Amplitude Spectra［J］.Int J Con⁃trol，1979，30（5）：871-884.

［12］Van der Ouderaa A，Schoukens J，Renneboog J.Peak Factor Mini⁃mization Using a Time-Frequency Domain Swapping Algorithm ［J］.IEEE Trans Instrum Meas，1988，37：145-147.

朱燕梅（1986-），女，汉族，河北衡水人，在读硕士，主要从事自动化测试与控制技术，757086161@qq.com；

侯文（1967-）男，汉族，山西太原人，中北大学教授，硕士生导师，主要从事自动化测试与控制技术，动态测试与智能仪器的研究，13327512575@qq.com。

Schroeder Phased Harmonic Signal Applied in Frequency Response Test of Servo System*

ZHU Yanmei1，HOU Wen2*，ZHANG Yin1
（1.School of Instrument and Electronics，North University of China，Taiyuan 030051，China；2.School of Information and Communication Engineering，North University of China，Taiyuan 030051，China）

Schroeder phased harmonic signal with non-uniform power spectrum is used as the excitation source of frequency response test for servo system in order to reduce the testing time and improve test precision in the measur⁃ing.Using this signal can make the excitation more stationary due to its low peak factor.An experiment was conduct⁃ed on a steering gear.The experimental results show that the error of amplitude-frequency characteristic kept within ±0.069 dB and the error of phase-frequency characteristic kept within±0.602°and the testing time was reduced by 53.3%compared with the traditional sweep sinusoid signal.The system was stationary in the testing process.This signal is very suitable for rapid and high-precision test of frequency response.

servo system；frequency response test；SPHS；peak factor

TP273

A

1005-9490（2016）02-0361-04

EEACC：7120；014010.3969/j.issn.1005-9490.2016.02.023

项目来源：总装国防科技基金项目（9140C120402120C12055）

2015-05-22修改日期：2015-06-19