基于偏好知识的多目标优化算法求解计及电源侧的配电网故障恢复

姚玉海，王增平，张首魁，郭昆亚，金 鹏，齐 郑



基于偏好知识的多目标优化算法求解计及电源侧的配电网故障恢复

姚玉海1，王增平1，张首魁1，郭昆亚2，金 鹏2，齐 郑1

(1.新能源电力系统国家重点实验室(华北电力大学)，北京 102206；2.沈阳供电公司，辽宁 沈阳 110811)

针对传统故障恢复在处理电源侧问题上的不足，基于变电站主变在实际运行时要尽量满足-1准则的要求，提出了变压器越限个数和变压器平均负载率两个目标函数。在求解故障恢复的算法上，针对基于传统占优机制的经典多目标智能算法在迭代过程中没有考虑决策者的偏好知识，从而导致算法收敛缓慢和无法得到最优解的问题，将g占优机制和TOPSIS方法引入多目标智能算法。g占优机制中的参考点可以根据故障恢复问题的特殊要求进行灵活设计，TOPSIS方法可将决策者的偏好知识融入算法的迭代过程中。这些措施可以有效地提高解的质量和算法的收敛性能。最后，通过算例验证了该算法的可行性和有效性。

配电网；故障恢复；g占优机制；TOPSIS方法

0 引言

故障恢复是智能配电网自愈控制的一项重要内容，对配电网安全、经济、优质运行具有重要意义[1]。

我国配电网呈环形设计、辐射状运行，网络中存在大量的开关设备用以隔离事故和恢复负荷。当某个元件故障时，其下游负荷失电，可闭合和打开相关开关设备将这部分非故障失电负荷转移到其他馈线上，这就必然导致负责转供这部分负荷的上级电源负载加重[2-3]。现有成果在处理电源侧问题上，或认为变电站主变容量充足，而不加考虑；或将变电站主变容量作为约束条件，来保证故障恢复不会使得变压器的容量越限。事实上，我国变电站主变的运行是要满足-1准则的，即某台主变故障或检修，其所带母线上的所有负荷可由其他变压器转供，而不使其失电或部分失电[4]。在不考虑主变-1准则而进行故障恢复的情况下，不满足-1准则的主变发生故障将导致大范围的停电[5-7]。

近年来，在满足-1准则后的主变在最大供电能力问题上已有一定成果。文献[8]提出一种基于主变互联关系和-1准则的供电能力计算方法，可以得到各台主变的最大负载率。文献[9]研究了供电能力计算在联络容量限制与主变过载方面的改进方法，从而实现了一套完整的配电系统供电能力计算方法。

由于考虑了电源侧的因素，目标函数的个数将进一步增加。目前在处理多目标问题上大体上分为两类方法。一类是在偏好知识的基础上根据层次分析法等数学方法得到目标函数的权重，再采用权重将多目标优化问题转换为单目标优化问题[10-12]。

另一类是多目标优化方法，这种方法有效避免了权重值的影响。文献[13]论述了多目标优化问题转换为单目标优化问题的两个局限性，并在舰船电网背景下应用非支配排序遗传算法对故障恢复问题进行求解。文献[14-15]根据Pareto占优机制对故障恢复的解进行了等级划分，并采用改进的非支配排序遗传算法Ⅱ对配电网故障恢复问题进行求解。文献[16]提出了基于改进小生境遗传算法的Pareto求解多目标配电网重构。文献[17]针对Pareto占优机制没有有效利用目标的相对重要程度的问题，提出了一种E占优机制来求解多目标优化问题。该方法本质是将较优目标个数多的和较差目标个数少的故障恢复方案逐步筛选出，并且结合原点距离最小作为优劣判据，在电网转供能力充足的情况下，可以得到最优故障恢复方案。但在电网转供能力不充足的情况下，即在切负荷的情况下，切除负荷较多的方案往往具有更多个数的较优目标，该方法难以得到最优故障恢复方案。

针对上述问题，本文在主变最大供电能力问题的成果基础上提出了变压器越限个数和变压器平均负载率两个目标函数用以配电故障恢复。采用基于g占优和TOPSIS方法的多目标智能算法求解配电网故障恢复问题。

1  目标函数和约束条件

在配电网故障恢复问题中涉及的指标如下。

失电负荷量1是非故障失电区域负荷中未能被恢复的负荷量。

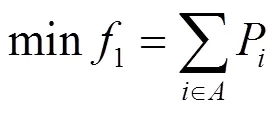
式中：为未恢复的节点集合；P为节点的负荷。

配电网在故障恢复之后，由于部分馈线转供了非故障失电区负荷，从而导致了为其供电的变压器负载率的必然升高。变压器越限个数2反映的就是变压器负载率升高之后，可能导致的不再满足最大负载率的变压器个数。在实际工程中，我们希望的故障恢复方案使得违反-1准则的变压器越少越好。值得说明的是，变压器违反最大负载率不同于违反其额定容量，在工程实际中并不需要强制切除负荷。

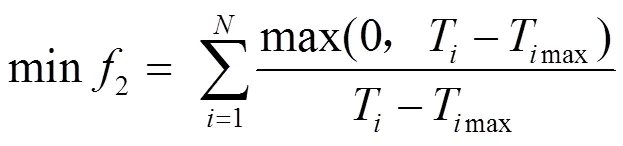
式中：T为变压器的实际运行负载率；Tmax为变压器在满足变压器-1条件下的最大负载率；为变压器的个数。

变压器平均负载率3反映的是配电系统的变压器的负载率的平均值，本身没有物理意义。配电网故障恢复之后导致了部分负荷的重新分配，此时的恢复方案可分为两类。第一类是恢复方案必然导致某些变压器违反-1准则。因为不同变压器的额定容量或有不同，在设计目标函数时，以“能者多劳”的原则来使得绝对剩余容量大的变压器来更多地转供负荷，这样可使得配电系统的电源侧保持较好的裕度。例如，1号变压器和2号变压器的最大负载率和故障恢复前负载率均为50%，其额定容量分别为10 MVA和20 MVA，因为2号变压器的绝对剩余容量较大，所以希望2号变压器来转供负荷。假如负荷由1号变压器转供则其负载率变为60%，则两台变压器的平均负载率为55%，其中1号变压器违反了-1准则；假如负荷由2号变压器转供则其负载率变为55%，则两台变压器的平均负载率为52.5%，其中2号变压器违反了-1准则；这样在同样变压器越限个数的情况下，平均负载率使得绝对剩余容量大的变压器承担了更多的转供负荷。

第二类是恢复方案没有导致任何变压器违反-1准则。由于没有变压器违反-1准则，此时变压器负载率是否平均或合理并非故障恢复问题所考虑的重点，因此并不希望看到变压器的负载不均而导致的电网拓扑结构的大幅变化，所以引入了变压器越限因子。

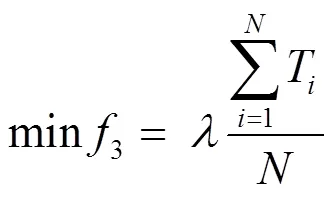
式中：为变压器越限因子，当有任一变压器负载率大于其最大负载率时，=1；所有变压器的负载率均小于其最大负载率时，=0。

开关操作次数4是衡量故障恢复快速性的重要指标，在恢复方案中要尽量减少开关的频繁动作。

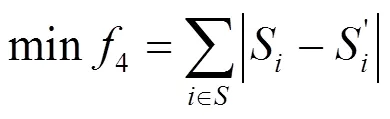
式中：为开关集合；S＇、S为恢复前后的开关状态。

网损5反映的是电网在故障恢复之后的电网有功损耗，为了保证电网运行的经济性，网络损耗要尽量小。

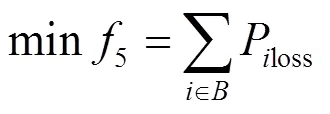
式中：为支路集合；Ploss为支路的网损。

配电网故障恢复需要满足的约束条件有：

(1)  配电网络的拓扑约束，故障恢复后的配电网拓扑结构为辐射状的连通网络。

(2)  配电网络的节点电压约束。

(3)  配电网络的支路电流约束。

(4)  变电站主变的容量约束。

2 g占优和TOPSIS法

2.1 g占优机制

为了说明g占优机制[18]，本文先对Pareto占优进行简要说明。为了不失一般性，均以最小化问题为例，最大化问题可以通过取反的方式转换。

Pareto占优[19]：针对多目标多约束问题，任意两个可行解1和2，如果满足式(6)，则称可行解1Pareto占优可行解2，也可称为1支配2。

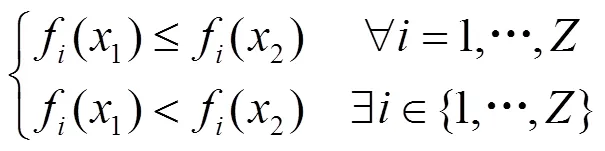
式中，表示目标函数的个数。

Pareto占优解类似于单目标问题中的最优解，在迭代过程中对算法的收敛方向有着重要的影响。从上述Pareto占优定义可以看出，可行解之间互不支配的情况较多，间接影响了算法的收敛效率。针对上述问题，本文采用g占优机制来进行多目标寻优。

给定一个参考点g和任一解的()定义如下：

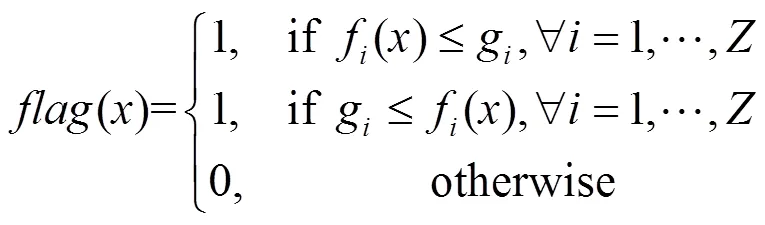
g占优：任意两个可行解1和2，如果满足下述条件之一，则称可行解1g占优可行解2。

(1)(1)>(2)；

(2) 若(1)=(2)，1在Pareto意义上占优2。

g占优的核心思想是通过设置一个参考点，将支配解(Pareto占优解)控制在偏好区域内，从而达到减少互不支配解个数对算法的影响。如图1所示的两个指标为例，图中实线弧为支配解，在参考点的作用下，flag区域为0的解将被剔除，从而减少了互不支配解的数量。

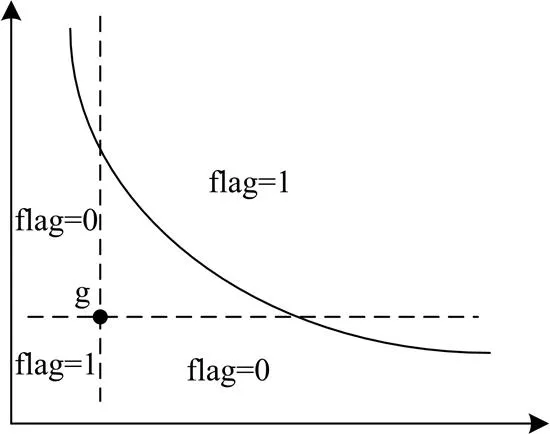
图1 参考点g影响下的flag区域

从图1可以看出，参考点的合理选择至关重要，它直接影响着解的存在区域。在故障恢复问题中，非故障失电区域负荷的恢复情况是问题的核心，本文在应用g占优时，采用上一次迭代过程中失电负荷量最小的值作为参考点，采用式(8)来计算解的flag。

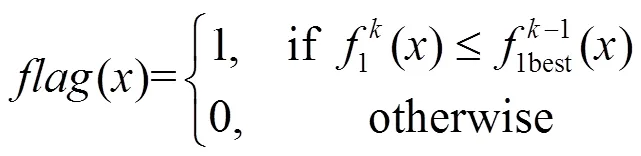
2.2 TOPSIS方法

多目标智能算法在迭代过程中，只考虑了支配解之间的客观分布[17]，没有考虑主观偏好知识，影响了算法的收敛速度。本文采用逼近理想解的排序方法[20](technique for order preference by similarity to an ideal solution, TOPSIS)使得算法中的种群个体在一定的选择压力下朝着优化前沿收敛。TOPSIS方法需要设置正负理想点，正理想点可理解为最优解，负理想点可理解为最劣解。正负理想点不受可行解约束，可仅代表主观偏好的趋势。

TOPSIS方法是一种逼近理想解的方法，在可行解中，找到最贴近正理想点的同时又最远离负理想点的解作为最终的解决方案。该方法首先定义了正理想点g和负理想点g-，对于任意可行解，其与正负理想点的距离用欧式距离定义，分别记为d和-，可行解的相对贴近度可用式(9)计算。

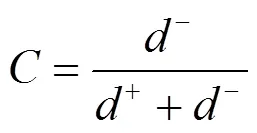
相对贴近度越大，表示该解离正理想点越近，同时离负理想点越远。

由于故障恢复问题中各个指标之间的量纲不同，在计算相对贴近度时需要对指标进行标准化，标准化时采用式(10)。

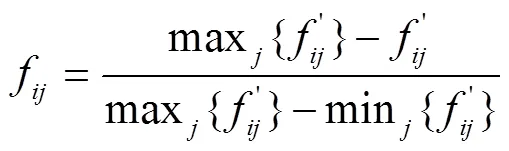
式中：f＇为第个方案的第个指标的有名值；f表示第个方案第个评价指标标准化后的值， fÎ[0,1]。

3  基于切负荷的编码方法

在保证配电网拓扑约束问题上，主要借鉴文献[11]所述破圈法来生成粒子位移，该方法可以随机生成一个连通的树状拓扑网络，可以满足网络重构的需求。但故障恢复属于故障后的网络重构，不完全等同于正常运行状态下的网络重构。网络重构问题中，重构前和重构后开关断开的个数相同。在故障恢复问题中，当电网失电负荷小于电网的转供能力时，故障恢复与网络重构在位移生成上并没有本质区别；但当电网失电负荷大于电网的转供能力时，则需要断开相应的开关切除部分负荷以满足工程实际，相当于将位移所对应的连通拓扑进行修正，以满足电压和电流约束。

3.1切负荷的基本原则

针对我国配电网特点，在切负荷时本文基于以下原则：

(1) 我国配电网呈辐射状运行，从末端开始向电源端的方向对负荷进行逐个切除，直到满足所有约束条件。

(2) 电流越限属于安全问题，电压越限属于电能质量问题，应先对电流越限进行切负荷，再对电压越限进行切负荷。

(3) 配电网故障恢复不仅要保证失电负荷最小，还要尽量保证重要负荷的持续供电。

(4) 尽量恢复失电负荷的前提下保证正常区域的持续供电，所切负荷应在非故障失电区域。

3.2位移编码

对负荷的重要性进行等级划分，负荷等级越高越不重要，在切负荷过程中优先切除等级高且大于越限量最小的负荷。并定义一条支路的两端节点中，潮流流出的节点为首节点，潮流流入的节点为尾节点。

基于切负荷的粒子编码步骤如下：

(1) 采用文献[17]所述破圈法来生成粒子位移。

(2) 对粒子位移所对应的拓扑结构进行潮流计算。

(3) 判断是否含有电压越限的节点或电流越限的支路。若不含有越限情况则不需要对当前位移进行修正；若存在电流越限则转步骤(4)；若仅存在电压越限则转步骤(5)。

(4) 以电源出口处支路为起点对电网支路进行广度优先遍历，将遍历结果中电流没有越限的支路删掉，得出以广度优先遍历顺序的所有电流越限支路集合。以电流越限支路集合中最后一个支路的尾节点为起始节点，向非故障失电区域方向对负荷节点做深度优先遍历，将搜索结果中正常区域的节点删除，在此基础上得到所有末端节点。将末端节点中负荷等级最高且负荷量大于支路越限量最小的节点切除，对切负荷之后的电网进行潮流计算之后转步骤(3)。若没有这样的节点存在，则将末端节点中负荷等级最高且支路越限量与负荷量差值最小的节点切除，再重复上述末端节点的切除办法，直到切除量大于支路越限量，对切负荷之后的电网进行潮流计算之后转步骤(3)。

(5) 以电源点为起点对负荷节点进行广度优先遍历，将遍历结果中电压没有越限的节点删掉，得出以广度优先遍历顺序的所有电压越限节点集合。以该集合中最后一个节点为起始节点，向非故障失电区域方向对负荷节点做深度优先遍历，并将搜索结果中正常区域的节点删除，在此基础上得到所有末端节点。以越限电压节点为起始节点向非故障失电区域方向对负荷节点做深度优先遍历，将搜索结果中正常区域的节点删除，在此基础上得到所有末端节点。将末端节点中负荷等级最高且负荷量最小的节点切除，对切负荷之后的电网进行潮流计算之后转步骤(3)。

4  多目标二进制粒子群算法流程

本文将g占优和TOPSIS方法融入多目标二进制粒子群算法[17]，多目标二进制粒子群算法的主要步骤包括外部档案维护、个体极值更新和群体极值更新。算法流程如下：

(1) 输入基本电气信息，设置算法参数、正负理想点。

(2) 初始化粒子的速度和Sigmoid函数，采用本文所述方法生成粒子位移。

(3) 对位移初次评价中采用Pareto占优准则，将不受支配的解存入外部档案中，在外部档案中随机采取一个不受支配的解作为群体极值，当前粒子作为个体极值。

(4) 更新粒子的速度和Sigmoid函数，采用本文所述方法生成粒子位移。

(5) 对外部档案进行维护。

外部档案维护主要是决定新解是否能加入外部档案及外部档案中的解是否被淘汰。具体维护可分为以下四种情况：

(a) 若外部档案中存在某个解g占优新解，那么新解不能存入外部档案中；

(b) 若新解g占优外部档案的某个解，那么这个解就从外部档案中删除，并将新解存入外部档案中；

(c) 若外部档案中的解与新解互不支配，将新解存入外部档案；

(d) 由于外部档案的容量大小是有限的，当互不支配解的个数大于外部档案的容量时，求出所有解的相对贴近度，将相对贴近度较小的解删除，直至满足容量限制。

(6) 更新群体和个体极值。

个体极值的调整主要是根据粒子在第+1次迭代获得的新解与其第次迭代的个体极值进行比较。若第次迭代的个体极值g占优新解，则个体极值保持不变；若新解g占优第次迭代的个体极值，则将新解更新为个体极值；若新解与第次迭代的个体极值互不占优，则取两者中相对贴近度高的解更新为个体极值。

将外部档案中解的相对贴近度求出，再根据轮盘赌策略选择群体极值。这样就使得群体极值的选择可以受到决策者的偏好知识的指导，同时因为也有一定概率选择相对贴近度较小的解，在一定程度上保证了种群的多样性。

(7) 判断是否满足收敛条件，若不满足则跳转步骤(4)；否则输出当前外部档案。

5  算例分析

本文采用如图2所示的3馈线配电系统为例，该电网额定电压为23 kV，基准容量为100 MVA，总负荷为28.7+j17.3 MVA，共有16个节点、16条支路，本文假设16条支路均装设开关设备，图中实线和虚线分别表示处于闭合和断开状态，节点负荷和电容器容量参考文献[21]。本文以图2所示运行方式进行计算，得出网络总损耗为511.44 kW，三条馈线出线电流为：1-4(394.13 A)、2-8(691.61 A)、3-13(223.53 A)。为了说明本文所述方法，对上述3馈线配电网络进行了改进，增加了上级变压器及母线所带其他馈线负荷，设定16条支路的额定容量为750 A，16个节点负荷的重要性相同。变压器最大供电能力的计算非本文重点，所以将其值直接给出。将变电站母线上其他馈线负荷等效为load1、load2、load3，变压器容量及其最大供电能力见表1。

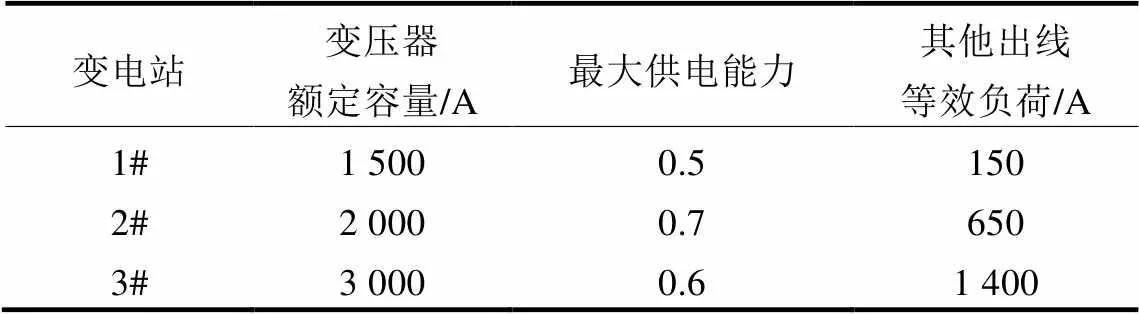
表1 电源侧基础数据

在多目标二进制粒子群算法中，种群规模和外部档案容量取为30，惯性权重取为0.5，学习因子都取为2，最大迭代次数取为20。正理想点设定失电负荷量为0，变压器越限个数为0，变压器平均负载率为0，开关操作次数为1，网损为总有功功率的1%(287 kW)。负理想点设定失电负荷量为28.7 MW，变压器越限个数为3，变压器平均负载率为1，开关操作次数为10，网损为总有功功率的10% (2 870 kW)。本文以失电负荷量1、变压器越限个数2、变压器平均负载率3、开关操作次数4和网损5为指标。

算例1：假设3-13发生永久性故障而退出运行。表2为本文方法所得出的最优解，即互不g占优的解，并且列出了各个解的相对贴近度。

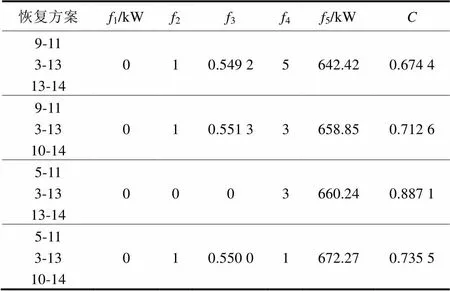
表2 故障恢复结果

在所述指标中，偏好知识是相对固定的。失电负荷量是故障恢复的根本目的，所以优先级最高。由于变压器作为电源在配电系统中的地位非常重要，工程上希望主变均满足-1准则。若变压器必然违反-1准则，则希望裕度充足的变压器来多承担负荷，这些目标都是值得开关去动作的。网络损耗是经济性，认为其优先级最低。

根据所述偏好知识容易得出5-11、3-13、13-14为最优恢复方案，并且该方案的相对贴近度也最大(=0.887 1)，说明了TOPSIS方法可以有效地辅助决策。该方案完全恢复了失电负荷，保证了所有主变均在-1准则内运行，同时也付出了3次的开关操作。

若不计及主变-1准则，则方案5-11、3-13、10-14为最优方案，该方案只通过1次开关操作就恢复了所有的失电负荷，但该方案却导致了一台主变违反了-1准则，根据相对贴近度可以看出该方案为次优解。

算例2：假设2-8发生永久性故障而退出运行。表3为本文算法得出的最优解，表4为基于Pareto占优得出的最优解。

表3 基于g占优的故障恢复结果

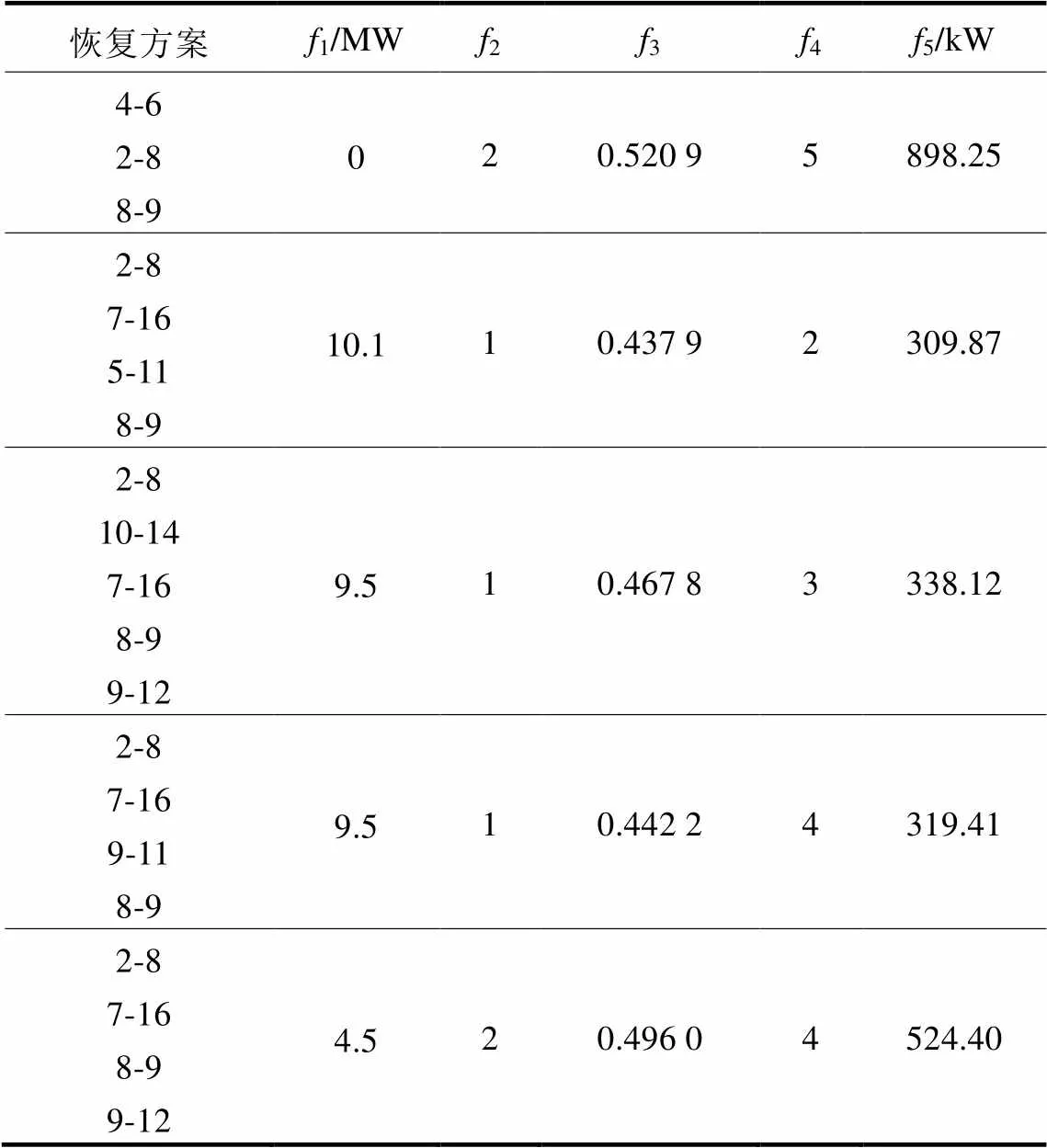
表4 基于Pareto占优的故障恢复结果

从表3和表4可以看出，方案4-6、2-8、8-9可将失电负荷完全恢复，所以该方案为最优恢复方案，并且g占优机制和Pareto占优机制均得到了该方案，但是本文采用的g占优机制得到的互不支配解的个数比Pareto占优要少。这是因为Pareto占优机制中将各个指标视为同等重要，而g占优机制的参考点设计可在迭代过程中将恢复负荷量较小的解逐步淘汰，这就使得g占优机制下的互不支配解的个数更少、质量更高，最终也方便运行人员进行决策。

由于不同占优机制得出的最优前沿是不同的，而故障恢复问题最终仅需其中的一个方案去指导工程实践。为方便这两种占优机制进行比较，表5给出了基于Pareto占优机制和拥挤距离的二进制粒子群算法和本文算法在100次单独计算过程中，方案4-6、2-8、8-9在迭代过程中出现的代数。基于Pareto占优机制和拥挤距离的二进制粒子群算法的平均迭代次数为17.3，而本文算法的平均迭代次数为11.6。

表5 迭代统计

可以得出本文算法迭代次数更少，更容易收敛。这是因为本文算法在迭代过程中采用的TOPSIS法考虑了偏好知识，“人为”地使粒子向希望的方向移动，从而加速了收敛。并且应用g占优机制所得到外部档案中的解比Pareto占优机制的解更加符合故障恢复要求，进而得到群体极值可以快速引领群体向最优解方向收敛。

算例3：假设1-4发生永久性故障而退出运行。在1-4发生故障的情况下，不存在可以完全恢复失电负荷的方案，所以需要切负荷，表6为本文方法所得出的最优解，表7为基于E占优得出的最优解。

表6 基于g占优的故障恢复结果

表7 基于E占优的故障恢复结果

从表6和表7所列方案可以看出，相较于E占优机制本文方法得到的恢复方案切除的负荷量较小，恢复的负荷更多。E占优机制得到的解在指标2、3、5上优于本文方法，这是因为E占优机制得出的是较优目标个数多的和较差目标个数少的故障恢复方案，在电网转供能力不充足的情况下，切除负荷较多的方案往往具有更多个数的较优目标，难以得到最优故障恢复方案。本文方法的参考点设计可在迭代过程中淘汰了恢复负荷量较小的解，使得故障恢复问题中的主要矛盾得以有效解决。

6  结论

通过变压器越限个数和变压器平均负载率两个目标函数的建立，可以使得故障恢复方案避免或尽量减少变压器违反-1准则，即使变压器在违反-1准则的情况下，也可以让裕度更大的变压器优先来转供负荷，以保证每台变压器均有一定的裕度来应对负荷的波动或其他突发事件。提出的基于g占优和TOPSIS方法减少了互不支配解的规模，改善了算法的计算效率和收敛性能，可以有效解决配电网故障恢复问题。

[1] 徐玉琴, 张丽, 王增平. 基于AER 模型的配电网大面积断电供电恢复算法[J]. 电网技术, 2009, 33(12): 66-71.

XU Yuqin, ZHANG Li, WANG Zengping. Agent- environment-rule model based algorithm of service restoration for large-area blackout of distribution system[J]. Power System Technology, 2009, 33(12): 66-71.

[2] 文娟, 谭阳红, 雷可君. 基于量子粒子群算法多目标优化的配电网动态重构[J]. 电力系统保护与控制, 2015, 43(16): 73-78.

WEN Juan, TAN Yanghong, LEI Kejun. Multi-objective optimization of distribution network dynamic reconfiguration based on integer coded quantum particle swarm optimization algorithm[J]. Power System Protection and Control, 2015, 43(16): 73-78.

[3] 孙元博, 张承学, 胡志坚. 基于图解蚂蚁系统的配电网动态重构[J]. 电力系统保护与控制, 2015, 43(12): 73-78.

SUN Yuanbo, ZHANG Chengxue, HU Zhijian. Dynamic distribution network reconfiguration method based on graph ant system[J]. Power System Protection and Control, 2015, 43(12): 73-78.

[4] 王增平, 姚玉海, 郭昆亚, 等. 基于等级偏好优序法和切负荷的配电网故障恢复[J]. 电工技术学报, 2015, 30(20): 185-192.

WANG Zengping, YAO Yuhai, GUO Kunya, et al. Distribution network service restoration based on rank preference optimal and load shedding[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 185-192.

[5] 沈鑫, 曹敏. 分布式电源并网对于配电网的影响研究[J]. 电工技术学报, 2015, 30(增刊1): 346-351.

SHEN Xin, CAO Min. Research on the influence of distributed power grid for distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 346-351.

[6] 张巍, 孙云莲, 胡雯, 等. 计及电网经济性的配电网供电恢复重构寻优算法[J]. 电网与清洁能源, 2013, 29(7): 41-45.

ZHANG Wei, SUN Yunlian, HU Wen, et al. Optimized reconfiguration algorithm for power supply recovery of distribution network with economy of power grid considered[J]. Power System and Clean Energy, 2013, 29(7): 41-45.

[7] 李辰雷, 卫志农, 韩连山. 序优化理论在配电网重构中的应用[J]. 电力系统保护与控制, 2015, 43(8): 41-48.

LI Chenlei, WEI Zhinong, HAN Lianshan. Application of ordinal optimization in distribution network reconstruction[J]. Power System Protection and Control, 2015, 43(8): 41-48.

[8] 王成山, 罗凤章, 肖峻, 等. 基于主变互联关系的配电系统供电能力计算方法[J]. 中国电机工程学报, 2009, 29(13): 86-91.

WANG Chengshan, LUO Fengzhang, XIAO Jun, et al. An evaluation method for power supply capability of distribution system based on analyzing interconnections of main transformers[J]. Proceedings of the CSEE, 2009, 29(13): 86-91.

[9] 葛少云, 韩俊, 刘洪, 等. 计及主变过载和联络容量约束的配电系统供电能力计算方法[J]. 中国电机工程学报, 2011, 31(25): 97-103.

GE Shaoyun, HAN Jun, LIU Hong, et al. Power supply capability determination considering constraints of transformer overloading and tie-line capacity[J]. Proceedings of the CSEE, 2011, 31(25): 97-103.

[10]徐玉琴, 张丽, 王增平, 等. 基于多智能体遗传算法并考虑分布式电源的配电网大面积断电供电恢复算法[J]. 电工技术学报, 2010, 25(4): 135-141.

XU Yuqin, ZHANG Li, WANG Zengping, et al. Algorithm of service restoration for large area blackout in distribution network with distributed generators[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 135-141.

[11]卢志刚, 杨国良, 张晓辉, 等. 改进二进制粒子群优化算法在配电网络重构中的应用[J]. 电力系统保护与控制, 2009, 37(7): 30-34.

LU Zhigang, YANG Guoliang, ZHANG Xiaohui, et al. Reconfiguration of distribution network based on improved particle swarm optimization[J]. Power System Protection and Control, 2009, 37(7): 30-34.

[12]雷绍兰, 王士彬, 胡晓倩, 等. 配电网供电恢复的混沌免疫算法[J]. 高电压技术, 2009, 35(6): 1492-1496.

LEI Shaolan, WANG Shibin, HU Xiaoqian, et al. Chaotic optimization integrated with artificial immune algorithm for distribution service restoration after faults[J]. High Voltage Engineering, 2009, 35(6): 1492-1496.

[13] 蒋燕君, 姜建国, 乔树通. 采用本质多目标进化算法的舰船电网故障智能恢复决策[J]. 中国电机工程学报, 2011, 31(31): 118-124.

JIANG Yanjun, JIANG Jianguo, QIAO Shutong. Intelligent service restoration of shipboard power network using nature multiobjective evolutionary algorithm[J]. Proceedings of the CSEE, 2011, 31(31): 118-124.

[14] 黄弦超, 张粒子, TAYLOR G. 考虑负荷控制的配电网故障恢复[J]. 电力系统自动化, 2010, 34(17): 22-26.

HUANG Xianchao, ZHANG Lizi, TAYLOR G. Service restoration of power distribution systems with load control[J]. Automation of Electric Power Systems, 2010, 34(17): 22-26.

[15]黄弦超, TAYLOR G. 基于节点深度编码技术的配电网故障恢复[J]. 电力系统自动化, 2011, 35(6): 40-44.

HUANG Xianchao, TAYLOR G. Service restoration of distribution networks based on node-depth encoding technique[J]. Automation of Electric Power Systems, 2011, 35(6): 40-44.

[16] 李伟, 张振刚, 闫宁. 基于改进小生境遗传算法的 Pareto 多目标配电网重构[J]. 电力系统保护与控制, 2011, 39(5): 1-5.

LI Wei, ZHANG Zhengang, YAN Ning. Pareto multi- objective distribution network reconfiguration based on improved niche genetic algorithm[J]. Power System Protection and Control, 2011, 39(5): 1-5.

[17] 姚玉海, 王增平, 郭昆亚, 等. 基于E占优的多目标二进制粒子群算法求解配电网故障恢复[J]. 电力系统保护与控制, 2014, 42(23): 76-81.

YAO Yuhai, WANG Zengping, GUO Kunya, et al. Distribution network service restoration using a multi-objective binary particle swarm optimization based on E-dominance[J]. Power System Protection and Control, 2014, 42(23): 76-81.

[18] MOLINA J, SANTANA L V, HERNÁNDEZ-DÍAZ A G, et al. g-dominance: reference point based dominance for multiobjective metaheuristics[J]. European Journal of Operational Research, 2009, 197(2): 685-692.

[19] COELLO C, CARLOS A, LECHUGA M S. MOPSO：a proposal for multiple objective particle swarm optimization[C] // Proceedings of IEEE Congress on Evolutionary Computation. USA, Honolulu: IEEE, 2002: 1051-1056.

[20]邱飞岳, 吴裕市, 邱启仓, 等. 基于双极偏好占优的高维目标进化算法[J]. 软件学报, 2013, 24(3): 476-489.

QIU Feiyue, WU Yushi, QIU Qicang, et al. Many-objective evolutionary algorithm based on bipolar preferences dominance[J]. Journal of Software, 2013, 24(3): 476-489.

[21] CIVANLAR S, GRAINGER J J, YIN H, et al. Distribution feeder reconfiguration for loss reduction[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1217-1223.

(编辑魏小丽)

Multi-objective optimization algorithm based on decision preferences to solve distribution network service restoration considering power supply

YAO Yuhai1, WANG Zengping1, ZHANG Shoukui1, GUO Kunya2, JIN Peng2, QI Zheng1

(1. State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China; 2. Shenyang Power Supply Company, Shenyang 110811, China)

Traditional distribution network service restoration cannot completely satisfy the requirements of-1 security verification of transformer in station, and the corresponding mathematical model is constructed. Without considering the preference of decision maker in the iterative process, the classic multi-objective evolutionary algorithm, based on Pareto dominance criteria and crowding distance sorting method, is of slow convergence speed. This paper proposes a multi-objective binary particle swarm optimization based on g dominance and technique for order preference by similarity to an ideal solution (TOPSIS) to solve distribution network service restoration. The reference point of g dominance can design flexibly according to the requirements of service restoration, and TOPSIS makes the preference of decision maker into the iteration. These improved measures are of great significance on improving the quality of solution and enhancing convergence velocity. Finally, an example is illustrated to verify feasibility and validity of the proposed method.

distribution network; service restoration; g dominance; TOPSIS

10.7667/PSPC150651

国家电网公司科技项目资助(合同号：沈阳供电公司信息化工作办公室KJ[2013]896)

2015-04-19

姚玉海(1986-)，男，通信作者，博士研究生，主要研究方向为电力系统自愈控制；E-mail: yao_yuhai@163. com

王增平(1964-)，男，教授，博士生导师，研究方向为电力系统保护与控制；E-mail: wangzp1103@sina.com

张首魁(1994-)，男，硕士研究生，研究方向为配电网故障恢复。E-mail: shoukuizhang611@163.com