BNR中参考信号多径对对消的影响分析
鲁振兴,洪永彬,付 伟
BNR中参考信号多径对对消的影响分析
鲁振兴,洪永彬,付 伟
(中国电子科技集团公司第五十四研究所,河北石家庄050081)
双基地噪声雷达 (BNR)中,参考信号中的多径成分会明显降低回波通道中直达波和杂波的对消性能。基于维纳滤波原理,推导出了对消器输出的均方特性,并讨论了参考信号多径的影响。分析表明,参考信号中的多径成分会引起远距离杂波对消性能的明显下降,并且随着多径成分的增强,直达波和近距杂波的对消性能也会明显降低。通过仿真验证了理论分析的有效性。
双基地噪声雷达;杂波对消;参考信号多径
引用格式:鲁振兴,洪永彬,付 伟.BNR中参考信号多径对对消的影响分析[J].无线电工程,2016,46(5):37-40.
0 引言
由于具备良好的低截获和抗干扰特性[1],噪声雷达近年来得到了广泛的关注[2]。然而,在连续波体制的噪声雷达中,发射信号的泄漏会明显降低微弱目标的检测性能[3]。在双基地噪声雷达(Bistatic Noise Radar,BNR)中,尽管发射信号的泄漏明显减小,但是回波通道中的直达波和杂波信号仍然远远强于目标回波及接收机噪声[4]。为改善目标检测性能,在相关处理之前必须对直达波和近距杂波进行抑制[5]。
多数直达波和杂波对消方法中[6-7],均假设参考信号为发射信号延迟后的样本。实际中,参考通道中总是存在多径信号以及接收机噪声,这些非理想性成分会明显降低对消的性能。当参考通道中仅存在直达波信号和接收机噪声时,文献[8]给出了对消比会受限于参考通道信噪比的结论。当参考通道存在多径成分时,对消性能会明显下降[9]。文献[9]采用了恒模算法(CMA)对参考通道进行均衡处理,但在双基地噪声雷达中,由于发射信号具有随机的幅度特性,该方法并不适用。
在参考信号存在多径的情况下,理想对消器变为一个IIR结构的自适应滤波器,在实际中难以实现。通常双基地噪声雷达会采用FIR结构自适应滤波器进行对消处理,此时参考信号多径的影响非常明显。通过理论推导对参考信号中多径成分对直达波和杂波对消的影响进行分析,并通过数字仿真进行验证。
1 信号模型
一种典型双基地噪声雷达的接收系统原理框图如图1所示[8]。
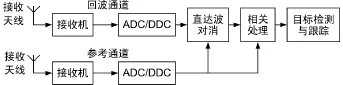
图1 典型双基地噪声雷达的接收系统
为检测目标,必须在回波信号和参考信号之间进行相关处理。然而,在回波通道中,直达波和杂波会远远强于目标信号。此时,即使经过相关处理,直达波和杂波信号的旁瓣仍然会淹没目标[10]。因而,必须在相关处理之前对直达波和杂波进行对消[11]。将参考通道的接收信号表示为:
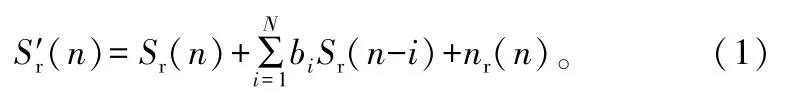
式中,Sr(n)为直达波信号(理想参考信号);bi为第i个多径信号的复幅度;N为参考通道中的多径成分存在分布的距离范围;nr(n)为接收机噪声。
假设回波通道中的杂波存在于前M个距离单元内,此时,回波通道的接收信号可以表示为:
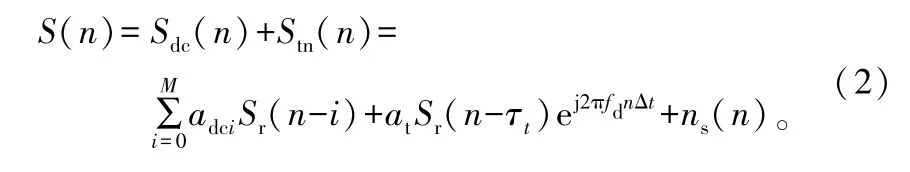
2 参考信号多径对对消的影响分析
首先,假设参考通道中的噪声分量足够小,可以忽略。此时,理想的对消模型如图2所示。
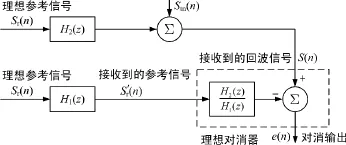
图2 对直达波和杂波的理想对消模型
图2中,
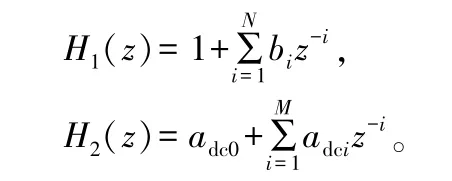
可以看出,理想的对消器具有IIR结构:
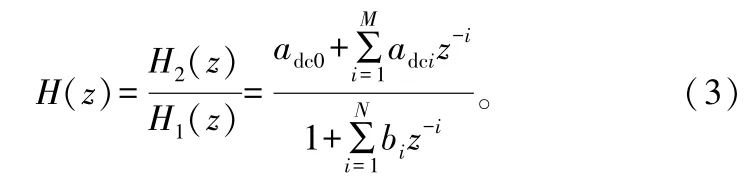
实际中,自适应的IIR滤波器难以实现,通常会采用FIR滤波器进行对消。而采用FIR结构的对消器会引起对消性能的下降。
2.1 对消器输出特性分析
因为直达波信号通常远强于多径成分,所以H1(z)的零点会位于单位圆内。此时,H1(z)的逆可以表示为[8]:

为简化分析,假设直达波Sr(n)的采样点之间彼此不相关,并且bi足够小,此时S′r(n)可以认为是白噪声。对于一个系数为h(n)的M阶维纳滤波器,对消输出可以表示为:
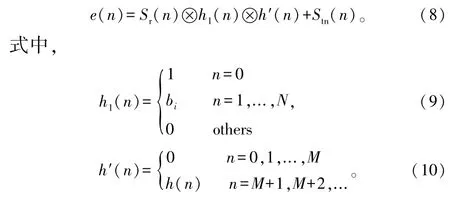
此时,对消器输出的均方误差为:
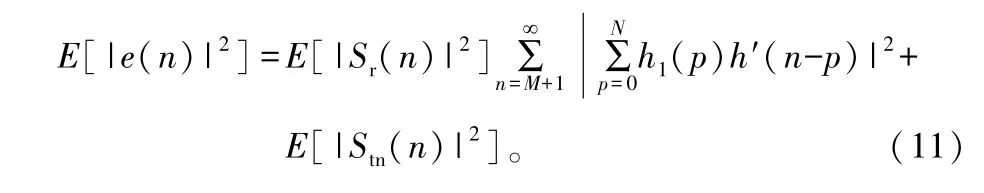
由式(5)可知,ci的表达式具有迭代形式,对式(11)进行分析非常困难。为简化分析,首先假设回波通道中仅第m个距离单元存在杂波,即仅adcm非零。此时,有h(n)=0,n<m,所以,对第m个距离单元杂波对消的有效延迟数仅为M-m+1。因此,对消器对直达波信号的对消性能最好,而对第M个距离单元杂波的对消性能最差。
实际情况下,回波通道中的直达波和近距离杂波要明显强于远距杂波,因此,总的对消性能下降并不是十分严重。当参考通道中不存在多径信号,即bi=0时,对i>0,有ci=0。此时,根据式(7)和式(10)可知,对于n>M,有h(n)=0以及h′(n)=0。对消器输出的均方误差
2.2仅存在一条多径的情况
考虑一种简单的情况:b1≠0,而对i>1,bi=0,即参考通道仅存在一条多径的情况。此时,有ci=(-b1)i。
对于直达波的对消(仅adc0非零),有h(n)= adc0(-b1)n,以及
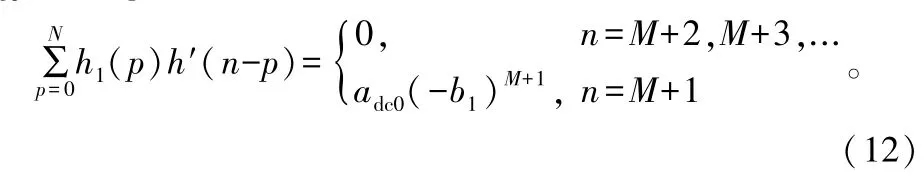
将式(12)带入式(11),可以得到:
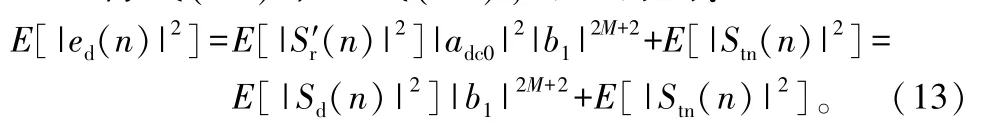
式中,Sd(n)为回波通道中的直达波。如果忽略式(13)中右手边第2项,对消剩余的功率将为接收直达波信号的|b1|2M+2倍。对于M=10,b1=0.3,最优对消器对直达波信号的对消比可以达到115 dB。实际上,只要满足E[|Sd(n)|2]|b1|2M+2<<E[|Stn(n)|2],参考信号的多径效应就可以忽略。
而对于第m个距离单元杂波的对消(仅adcm非零),有
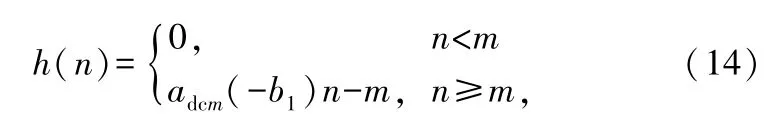
以及
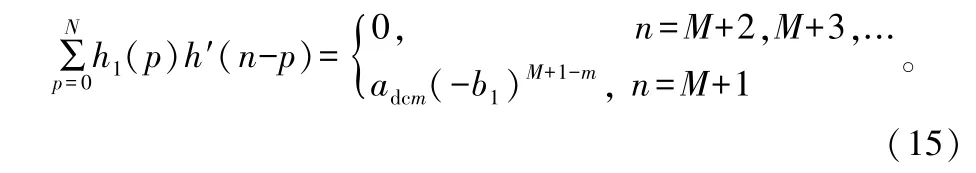
此时,对消器的输出功率变为:

可以看出m越大,对消性能越差。对于m=M,b1=0.3,对消比仅为10 dB。
尽管上述分析是基于最优维纳滤波器的,但该结果对很多自适应滤波器(比如常用的LMS滤波器)仍然适用,因为自适应滤波器收敛后的均方误差通常正比于维纳滤波器[12]。
3 仿真分析
仿真中,理想参考信号Sr(n)设为一高斯白噪声,对消器的阶数为M。对消器的系数更新算法采用LMS算法,算法中步长参数μ设为0.2/(MSmax),其中Smax为参考信号S′r(n)的功率谱最大值。此时,算法收敛后的对消比与理想维纳滤波器非常接近[13]。
3.1 仅存在一条多径的情况
下面的仿真中将考虑参考通道中仅存在一条多径信号,即N=1时的对消性能。假设对消器阶数M=10,回波通道中目标回波与接收机噪声的总功率为0 dB。
如果回波通道中仅第m个距离单元存在杂波(或直达波),当m分别为0,5和M时,对消比随b1的变化如图3所示,其中杂波或直达波的功率为60 dB。
图4还给出了当回波通道中的直达波和杂波具有不同幅度分布时的对消结果,其中对于不同的分布直达波和杂波的总功率均为60 dB。
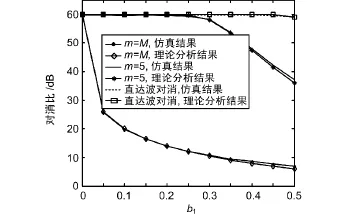
图3 对第m个距离单元杂波的对消结果
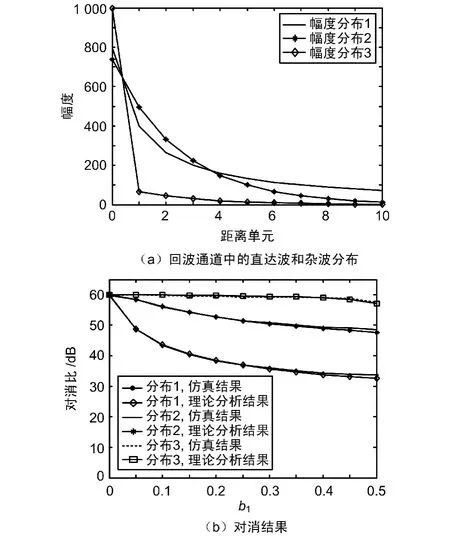
图4 不同分布杂波的对消结果
由图3可以看出,随着b1增大,对消比将逐渐减小。对于直达波信号的对消而言,参考信号多径导致的对消比降低非常小;但是,当m=M时,对消性能的下降将十分明显。该结果与理论分析一致。当b1较大时,理论分析与仿真结果之间存在很小的误差。这是由于在式(8)的推导中,假定S′r(n)为白噪声,对于较大的b1该假设是不成立的。由图4可以看出,近距离杂波越强,参考信号多径对对消结果的影响越小,该结果与理论分析仍然是一致的。
3.2 存在N条多径的情况
下面的仿真中将考虑参考通道中存在N条多径的情况。参考通道和回波通道中多径(杂波)的分布如图5所示,其中多径数量M=N=50。参考通道中直达波与多径信号之比(DMR)为10 dB。回波通道中直达波和杂波总强度大约为40 dB。参考通道和回波通道中多径信号强度分布大致按1/p2变化(不过会有一定起伏),其中p代表第p个距离单元。回波通道中目标回波与接收机噪声的总强度为0 dB,目标位于第70个距离单元,信噪比为0 dB。
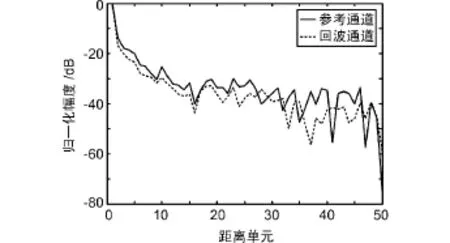
图5 参考通道和回波通道中的多径(杂波)分布
基于上述分布在对消前后进行距离多普勒处理。对消前,由于直达波和杂波很强,目标淹没在噪声基底中。对消后,噪声基底下降了大约39 dB,可以实现目标检测,然而,参考信号多径会使得对消后出现虚假杂波。对于该现象的解释可以参考文献[14],在此不再赘述。
4 结束语
双基地噪声雷达中,由于参考通道中存在多径成分,最优对消器具有IIR结构,采用FIR结构的对消器会引起对消性能的明显下降。在直达波和杂波的对消中,讨论了参考信号多径带来的影响,并以解析形式给出了分析结果。在相同的参考信号多径条件下,直达波和近距离杂波的对消效果要好于远距离杂波。
[1] GARMATYUK D S,NARAYANAN R M.ECCM Capabili-ties of an Ultrawideband Bandlimited Random Noise Imaging Radar[J].IEEE Transactions on Aerospace and E-lectronic Systems,2002,38(4):1 243-1 255.
[2] AXELSSON S R J.Noise Radar Using Random Phase and Frequency Modulation[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(11):2 370-2 384.
[3] MALANOWSKI M,KULPAK.DetectionofMoving Targets with Continuous-wave Noise Radar:Theory and Measurements[J].IEEE Transactions on Geosciences and Remote Sensing,2012,50(9):3 502-3 509.
[4] HOWLAND P E,MAKSIMIUK D,REITSMA G.FM Radio Based Bistatic Radar[J].IEE Proc.Radar Sonar Navig,2005,152(3):107-115.
[5] AXELSSON S R J.Suppression of Noise Floor and Dominant Reflectors in Random Noise Radar[C]∥Proceedings of International Radar symposium,2006:1-4.
[6] 邹 敏,纪学军.射频自适应干扰抵消系统的分析与设计[J].无线电工程,2011,41(4):39-41.
[7] 曹 琦,宋春林,柏 亮,等.一种基于归一化的抗同频干扰算法[J].无线电通信技术,2013,39(5):29-32.
[8] LU Zhen-xing,GAO Mei-guo,LI Yun-jie,et al.Performance Analysis of Direct Signal and Surface Clutter Cancellation for Bistatic Noise Radar with LMS Filter[C]∥10th IEEE International Conference on Industrial Informatics,2012:184-189.
[9] CARDINALI R,COLONE F,LOMBARDO P,et al.Multipath Cancellation on Reference Antenna for Passive Radar which Exploits FM Transmition[C]∥IET International Conference on Radar Systems,2007:1-7.
[10]MELLER M,TUJAKA S.Block Least Mean Squares Processing of Noise Radar Waveforms[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):749-761.
[11]王 俊,赵洪立,张守宏,等.非合作连续波雷达中存在强直达波和多径杂波的运动目标检测方法[J].电子学报,2005,33(3):419-422.
[12]MANOLAKIS D G,INGLE V K,KOGON S M.统计与自适应信号处理[M].北京:电子工业出版社,2003:487-490.
[13]HAYKIN S.自适应滤波器原理(第4版)[M].北京:电子工业出版社,2003:202-218.
[14]KULPA K.The Effect of Target Presence in Reference Channel of Bistatic Noise Radar[C]∥International Radar Symposium,2008:1-4.
Analysis of Reference Multipath Effect on Signal Cancellation for BNR
LU Zhen-xing,HONG Yong-bin,FU Wei
(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081)
For bistatic noise radars(BNR),the reference multipath will degrade the cancellation performance of the direct signal and clutter in surveillance channel.Based on the principle of Wiener filter,the mean square of canceller output is derived and the effect of reference multipath is discussed.It is shown that the reference multipath will lead to a severe performance degradation for long-range clutter cancellation.As the multipath increases,the direct signal and short-range clutter cancellation performance will also degrade significantly.The effectiveness of the analysis is demonstrated by numerical simulations.
bistatic noise radar;clutter cancellation;reference multipath
TP391.4
A
1003-3106(2016)05-0037-04
10.3969/j.issn.1003-3106.2016.05.10
2016-01-08
国家部委基金资助项目。
鲁振兴 男,(1984—),博士,工程师。主要研究方向:雷达信号处理、电子对抗。
洪永彬 男,(1983—),博士,工程师。主要研究方向:雷达信号处理、数字电路设计。

